基于灰色-小波神经网络模型的铁路路基沉降预测分析
吴 建 胡增明
(1.广东省国土资源测绘院,广东 广州 510500;2.安徽铁建工程有限公司,安徽 蚌埠 233000)
铁路运输作为国家基础性建设,它能够为旅游、交通运输带来极大的便利,同时大量的建设也需要技术支撑。随着科技的快速发展,铁路路基沉降监测得到推广。建立何种模型将采集的有限数据准确预测其变形趋势成为监测的关键技术,也是为工程数字预警提供良好的可靠性理论。
目前国内外工程施工过程中有关变形监测数据处理方法[1]有很多,主要包括卡尔曼滤波、时间序列及灰色理论等。由于铁路路基测量过程中观测数据贫乏,且铁路路基沉降监测的不确定因素较多,因此寻找适合于铁路路基沉降预测模型尤为重要。
卡尔曼滤波计算模型相对较复杂,且精度受初始状态估计较灵敏,因而只适用于线性模型的数据预测;时间序列是在赋予远期较小比重而近期比重较大情况下进行的短期预测,无法有效进行变形数据远期反馈;灰色系统理论[2]是基于相关数据关联度进行预测,其建立的灰色模型能反映未来数据变化特性。与其他预测方法相比,灰色预测模型往往所需数据不多,预测精度较高。
1 基本原理与概述
1.1 灰色理论
灰色理论是由我国邓聚龙教授提出的一种数学方法。它是以“外延明确,内涵不明确”的“小样本,贫信息”作为研究对象的,其通过生成数据模型得到预测值的逆处理过程,如公式(1)所示。
式中:x0(n)为第n次观测值。
对原始数据列进行一次累加,生成新的数列,如公式(2)所示。
建立X1白化形式的微分方程,如公式(3)~公式(8)所示。
然后求出a后解白化微分方程,求出:
式中:k=1,2,...,M。
原始数据序列x(0)的还原值如公式(8)所示[5]。
如果误差在符合相应规范情况下,则该模型能反映真实变形特性。否则需要不断修正模型。
1.2 小波神经网络概述
小波神经网络的结构与BP神经网络类似,其包括输入层、隐含层和输出层。二者的区别主要在于隐含层的传递函数,小波神经网络将BP神经网络中常用的logsig函数或tansig函数替换为小波函数。小波神经网络的基本框架如图1所示。

图1 小波神经网络基本框架
图1中{x1,x2,...,xk}是小波神经网络基本框架的输入数据,{y1,y2,...,ym}是小波神经网络基本框架的输出数据,Wik和Wjk分别为小波神经网络不同层之间的权值。为文采用的是Morlet小波函数,如公式(9)所示。
式中:f(x)为加权和;β为平移因子;α为尺度因子。
小波神经网络隐含层和输出层计算如公式(10)、公式(11)所示。
式中:j=1,2,...l,k=1,2,...,m,h(j)为隐含层第j个节点的输出值,y(k)为输出层的结果,wij为输入层与隐含层之间的权重,wjk为隐含层到输出层权值;hj为小波函数,bj为小波函数hj的平移因子,aj为小波函数hj的伸缩因子;l为隐含层节点数m为输出层节点数。
小波神经网络算法训练步骤如图2所示。
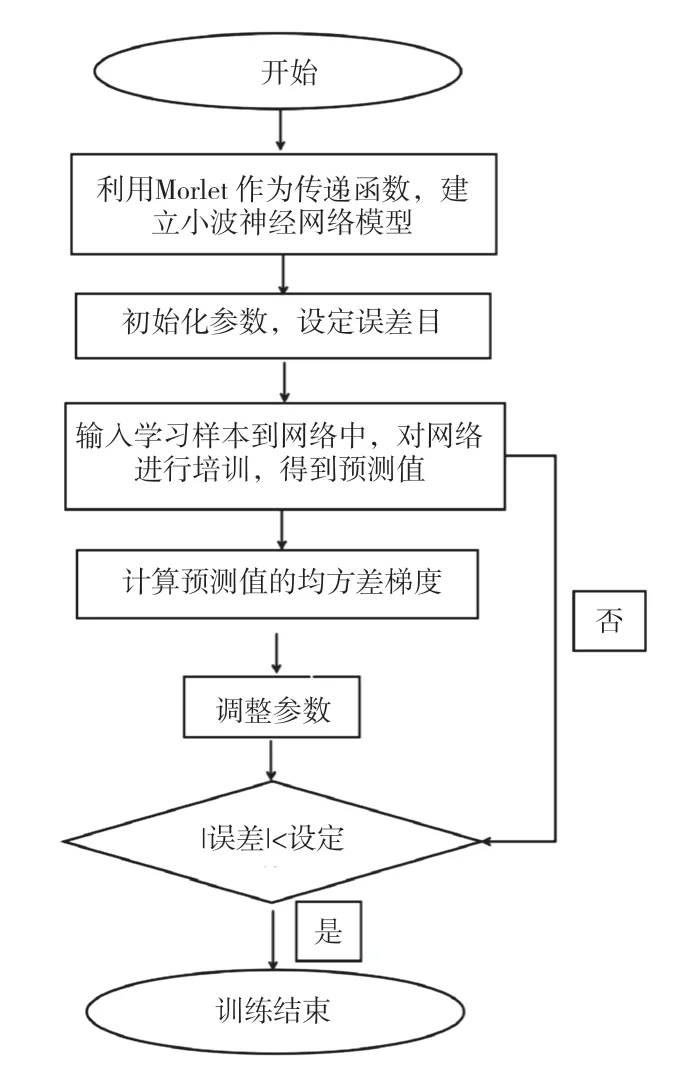
图2 小波神经网络算法训练图
由图2不难发现,小波神经网络模型利用小波函数作为隐含层的传递,从而建立相应的数学模型。该模型具有改进的BP网络特点,避免盲目性,具有较强学习能力,收敛速度更快,精度更高。
由于小波分析可在任意时间或空间域进行信号分析,其特点在非线性函数应用中较为明显,因此它改进了BP神经网络模型的优点,更适合学习局部非线性且变化快的函数。
1.3 灰色-小波神经网络组合模型
灰色理论在很多领域均有涉及,如文献[3]采用不同m值对土体孔隙水压力进行灰色模型预测,文献[4]通过灰色理论模型对深基坑监测数据进行了预测,文献[5]利用灰色理论、指数法和双曲线对铁路路基沉降进行预测分析评估,文献[6]利用灰色理论对桩基各级荷载建立灰色预测分析。这些方法都很好地验证了预测结果与实测值之间的差值,但是单一的灰色模型[7]往往在复杂的情况不能解决多方面因素影响,例如突发暴雨天气可能会增加铁路路基变形,小波神经网络方法在处理数据模糊的情况下可以发挥优势[8]。
鉴于以上原因,笔者结合上述两种方法,即采用嵌入式的小波神经网络[9],首先引入灰色模型对观测数据进行预处理,然后将预处理后的数据作为小波神经网络结构的数据输入来源,原始观测数据作为期望数据输出,由此训练样本,并对模型精度进行分析。
2 工程实例分析
2.1 工程概况
宁芜线K69+515雨山九区道口平改立工程,位于马鞍山市既有湖南西路与宁芜线铁路平交道口,新建4孔箱涵,中孔箱身顶板厚0.60m,边墙厚0.65m,底板厚0.70m,箱身结构净高5.75m;边孔箱身顶板厚0.45m,边墙厚0.50m,底板厚0.50m,箱身结构净高6.10m。箱身采用铁路外预制顶进就位,采用D16型和D24型便梁防护线路。
桥址主要底层为粉质黏土,埋深1.40~10.40m,标高-1.17~8.49m,层厚7.00~21.10m,地基基本承载力σ0=200kPa,该层为箱底持力层,水位位于自然地面3m以下。
2.2 技术路线
该工程采用首先进行箱涵预制及条基制作,然后采用D16型和D24型便梁进行线路加固,最后开挖路基并顶进箱涵的施工方案。该施工方案在确保线路安全后,方能进行路基开挖,为了线路的安全,施工过程须对宁芜铁路(k69+400~k69+620)路基进行沉降监测。结合该工程特点,制定技术路线如图3所示。

图3 技术路线流程图
该文将小波神经网络和灰色理论结合起来,建立组合模型对铁路路基沉降进行预测分析,通过对比两者预测数据与实测数据进行分析,从而验证新模型的优点。笔者参考了铁路测量相关规范,工后沉降累计值不应大于15mm,沉降预测的可靠性应经过验证,观测时间间隔不少于3个月,且预测最终较差不应大于2mm。
2.3 点位埋设与监测数据
铁路路基沉降监测严格按照国家二等水准测量的要求进行,线路两侧分别设12个断面,共24个监测点。该项目沉降监测仪器采用电子水准仪Trimble Dini03,其观测精度能达到0.3mm。观测数据来源于铁路施工过程第三方监测数据,由多次观测周期得到的路基沉降量见表1、表2。

表1 铁路路基东侧累计沉降量(单位:mm)

表2 铁路路基西侧累计沉降量(单位:mm)
分析上表可知,线路中心路基累计沉降量较大,尤其监测点LJ6-2累计沉降量最大值达到4.1mm,但满足预估工后沉降值不超过15mm 的要求,而距离施工中心里程越远,累计沉降量逐渐减少,这可能受中心区域土方开挖扰动的影响。
2.4 工后沉降预测结果及分析
为验证组合模型的正确性及优越性,该数据选择变形最大监测点LJ6-2的50期观测数据进行分析,选择前35期作为训练样本,后15期与预测值进行对比,得到成果见表3,如图4、图5所示。

表3 灰色模型与组合模型预测对比 (单位:mm)
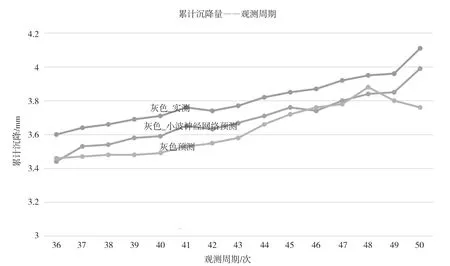
图4 灰色模型预处理数据与组合模型始数据对比
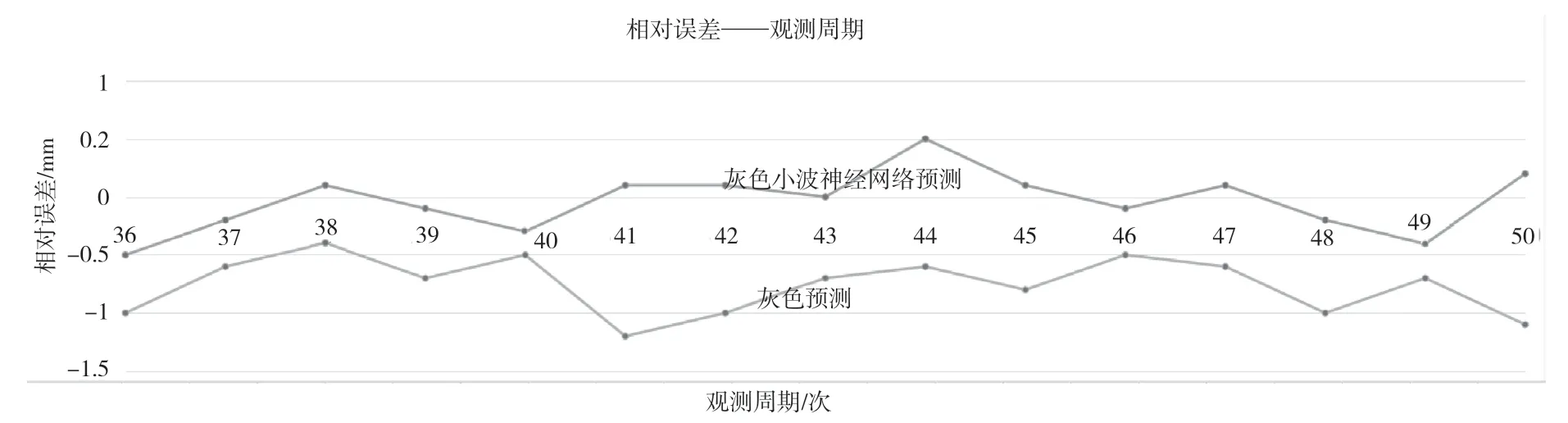
图5 灰色模型与组合模型相对误差对比
分析表3可知,单一灰色模型预测后期逐渐偏离实测值,而组合模型预测值的残差值明显比灰色模型小,更接近实测值。分析图4可知,随着时间的推移,灰色模型预测精度越来越低,最后呈现发散的状态,而组合模型则很好地弥补了这一缺陷。分析图5可知,组合模型的相对残差分布在-0.5~0.5,精度为二级等级,符合规范要求。以上说明组合模型在铁路路基沉降预测方面,预测精度明显有所提高,性能更加稳定。
3 结语
该文从变形体性质出发,结合工程特点,采用基于灰色模型与灰色-小波神经网络组合模型分别对铁路路基沉降进行预测分析,将实测数据与两种模型预测的数据进行对比分析,得到以下3个结论。1)通过比较灰色和灰色-小波神经网络两种建模预测铁路路基沉降变化,发现两种模型预测结果与实际值基本相近,都符合规范要求。2)灰色-小波神经网络模型较单一灰色模型,克服了后期发散缺点,精度有所高,稳定性更好。3)组合理论能有效的结合实测数据进行累加生成预测值,比较符合实际变化,进而建立组合模型进行预测,对铁路营业线安全施工提供数据支撑。

