基于故障诊断与可靠性分析的机械系统预防维修研究
张 鑫
(中煤北京煤矿机械有限责任公司,北京 102400)
目前,国内外对机械系统可靠性和可维修性的理论、方法研究已有较多成果[1]。随着机械装备的大型化、智能化、结构复杂化以及其在国民经济中的广泛应用,市场对机械系统的可靠性和维修性研究也越来越多[2]。机械设备在运行中不可避免地会发生各种故障,如生产运营方未能及时采取有效措施进行机械系统故障、异常现象的处理,会给企业生产经营带来巨大的损失。
根据现有研究可知,如果机械设备在运行中出现了故障,将会对企业的生产、生活甚至设备操作人员的生命财产造成很大影响[3]。为此,有必要对机械系统装备进行可靠性和可维护性的研究。同时,随着机械设备的日益复杂,其故障机理和模式更加复杂,单一的维护模式已无法适应现代化复杂装备的正常运转。如何及时发现设备的缺陷,并对其进行有效维护,是提高其可靠性和可靠性的关键[4]。具体而言,现代化维护策略的研究和实施,应从设备整体出发,根据设备的运行环境、人为因素等,在设备全寿命周期中,合理地制定维护策略,从而确保设备运行满足可靠性技术指标需求[5]。下文将对此进行详细研究。
1 机械系统轴承故障特征提取
为实现机械系统故障的诊断,进行研究前,需要先进行机械系统轴承故障特征的提取。在该过程中,设定机械设备轴承在一个周期内,将故障行为所引起的脉冲力表示为x(t),对x(t)进行描述,如公式(1)所示.
式中:A、τ代表机械系统轴承在运行中所产生的随机变量,主要是轴承的负载、随机滑动等因素对机械系统运行所造成的冲击影响;σ代表脉冲信号;t代表信号采样时刻点。
前端在接收到轴承运行所产生的激励响应后,由传感器收集轴承运行一个周期范围内的脉冲响应信号。此信号为y(t),对y(t)进行描述,如公式(2)所示。
式中:h(t)代表t时刻下由于机械设备轴承故障脉冲力所引起的系统整体响应信号;n(t)代表t时刻下采样所产生的响应信号。
在设备的实际操作过程中,由于轴承内圈及滚动体呈现周期性旋转特性,因此会导致轴承内圈(或者外圈)与滚动物体在局部失效位置发生接触时,也会呈现出一定的周期性[6]。在该基础上,将公式(1)进行拓展,并进行周期性脉冲力在延迟时间上的叠加处理,该过程如公式(3)所示。
式中:z(t)代表周期性脉冲力在延迟时间上的叠加脉冲力。
以此为依据,进行公式(2)的修正,如公式(4)所示。
在该基础上,采用带通滤波方法对轴承进行故障特征提取,提高其信噪比,以便更方便地辨识非稳态暂态信号。完成上述处理后,引进基于谱陡度的新方法,通过对信号频段的分析和处理,提高系统的信噪比[7]。以此为依据,提取机械系统轴承故障最大特征矢量,如公式(5)所示。
式中:R代表机械系统轴承故障最大特征矢量;λ代表平均特征矢量;R1代表最大循环次数;e代表特征值。
根据上文所述内容,提出对应的故障诊断方案,如图1所示。
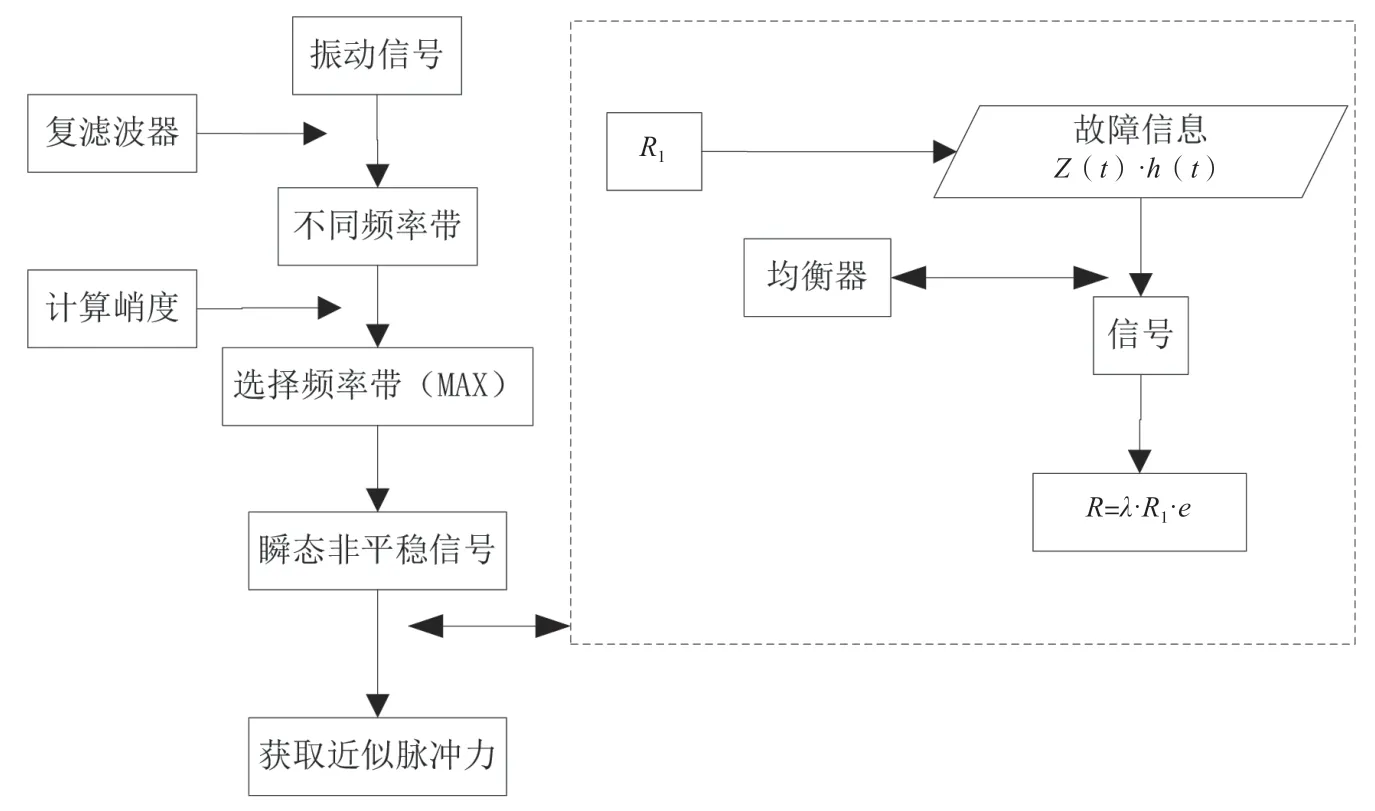
图1 机械系统轴承故障诊断
2 机械系统中部件可靠度分析
通常情况下,机械系统中设备维修主要包括预防维修与事前维修,该文研究的内容为预防维修,对预防维修构成进行分析,如图2所示。
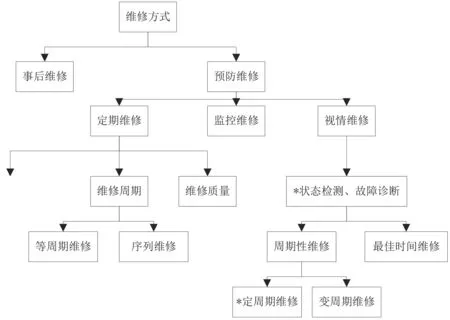
图2 机械系统中预防维修构成
在上述内容的基础上,为实现对系统中机械部件运行中可靠性的分析,可将机械设备的运行划分为2个阶段,以此为依据确定机械设备在运行中的缺陷点发生时刻,从而构建机械系统中部件缺陷延迟时间概念模型,如图3所示。
在上述内容的基础上,对机械系统中部件随运行时间的可靠度进行分析,如公式(6)所示。
式中:r(t)代表机械系统中部件随运行时间t的可靠度;Y(t)、D(t)代表机械系统中部件的独立随机运行过程;L、S代表在Y(t)、D(t)运行时段下的可靠度参照标准。
公式(6)也可以表示为公式(7)。
根据部件的实际运行情况,在公式(6)或公式(7)中代入2个独立随机运行时段,如满足上述公式,说明机械系统中部件在安全范围内运行,即机械系统中的部件在该时段下的可靠度较高;反之,如不满足上述公式,说明机械系统中部件未在安全范围内运行,即机械系统中部件在该时段下的可靠度较低。以此为依据,完成机械系统中部件可靠度分析。
3 建立非完好预防维修模型
完成对机械系统轴承故障特征的提取和对机械系统中部件可靠度的分析后,结合得到的分析结果,建立非完好预防维修模型,用以实现对机械系统的预防性维修。在考虑机械系统失效变形的条件下,假设机械系统在运动的初始阶段,最初的失效率为0。然后在没有任何维修手段的干预下,机械系统的失效率会逐渐增加。如果机械系统在运行的过程中对其进行了预防性地维修,则机械系统的失效率在维修后会逐渐恢复到0。结合该特点,在对机械系统进行第i次预防维修之后,机械系统的失效率可以用公式(8)表示。
式中:ζ代表机械系统的失效率;Ai代表机械系统失效率的调节系数,也可将其看作是机械系统性能改变因子;λi-1(t)代表t时机械系统的失效率函数。其中,t属于(0,ti-ti-1),Ai的取值应大于1。
通过上述公式描述可以得出,在第i次预防性维修后,机械系统的失效率为0,但其失效率的变化斜率在下一个检测周期中仍然会呈现增加的趋势,并且随着Ai的取值不断增加,机械系统的失效率变化斜率也会越来越大。
在考虑役龄回退的预防维修条件下,机械系统的失效率假设为λ0(t),其中t的取值为0~t1,并且在不采取任何维修措施的情况下,机械系统的失效率会呈现单调递增的变化趋势。当机械系统的时间时间达到t1时刻时,对该机械系统进行预防性维修,在维修后机械系统的失效率如公式(9)所示。
式中:α0代表虚拟役龄回退因子。α0取值为0~1。
通过这一公式可以得出,在进行预防性维修完成后,机械系统的实际役龄与虚拟役龄都为TP1,而在完成预防性维修之后,机械系统的实际役龄可表示为t+t1,虚拟役龄可表示为t+α0t1。在这种情况下,虚拟役龄通常比实际役龄要短,机械系统的健康状况是在完成预防性维修之后达到了更好的状态。因此,此时机械系统的故障率对应虚拟役龄的函数,每次预防性维修完成后,虚拟役龄都会有一定程度的下降。
通过上述运算可以得出,调节因子和役龄回退因子都能够实现对机械系统维修效率的直接描述。当完成预防性维修后,调节因子与役龄回退因子还会对机械系统的失效率产生更加直接的影响。在充分考虑随机维修程度的情况下,假设在第i次预防维修前,其失效率λi的递推关系可表示为公式(10)。
式中:Ai代表在第i次预防性维修之后的调节因子;αi代表在第i次预防性维修后的役龄退回因子。
Ai和αi均服从相应的分布函数为Gi(Ai)和Fi(αi)的随机变量。构建上述非完好预防维修模型时,将维修质量看作具有随机性的变量,以此能够进一步提高模型的合理性,同时也能使构建的模型更加满足机械系统可靠性分析的要求条件。
4 构建维修策略模型与维修策略制定
构建维修策略模型时,在机械系统运行的过程中如果遭受持续性恶化且有限时间内由新系统更换代替,制定维修策略时需要在更换周期内完成预防维修活动,以减少机械系统持续恶化,使其能够快速恢复到更好的状态。结合维修活动的实际所需,预防性的维修应当安排在周末或其他闲暇时间。在一个预防性维修周期中,机械系统可能发生故障并且可能造成机械系统停止运行,此时需要立即采取最小维修恢复机械系统,使其能够达到正常的工作状态。预防性维修模型中更换周期示意图如图4所示。

图4 预防性维修模型中更换周期示意图
图4中机械系统运行的有效时间为T0,在该时间内共设置了N次预防性维修,将每一个预防维修的周期间隔时间设置为Tpi。结合机械系统在运行过程中的不同状态,在该间隔中时间长短Tpi的取值不同。每一个预防维修周期的风险函数如公式(11)所示。
式中:λi(t)代表在第i次预防性维修周期当中的失效率函数;Tpi代表介于第i次和第i+1次之间的预防维修活动时间间隔。
经过最后一次维修后,介于第N次维修到机械系统更新之间的系统风险函数可通过上述公式变换得到。在该过程中,设置一个周期内总费用期望值,将计算结果与该数值进行对比,如果计算结果小于期望值,则可以采用该方法对机械系统进行预防性维修;反之,如果计算结果大于或等于期望值,则不可以采取该方法对机械系统进行预防性维修,应重新选择维修策略,并完成上述运算操作,直到计算结果小于期望值为止。
5 结语
随着我国装备制造行业、机械生产行业的快速发展,对装备的维护尤其是对大型机械装备的维护已引起科研人员和有关企业的广泛关注。在当前广泛应用的维修方式中,预防性维修占有十分重要的地位,是各企业对其设备进行维修安排的首选。截至目前,预防性维护已经发展了数十年,其理论已经相对成熟,维护策略和模型的内容也非常丰富,可以为维护工作的实践操作提供基础和参考。但要将该文提出的内容在相关领域内推广,还需要在此次研究成果的基础上结合行业发展的具体需求,进行各方面工作的深化,以确保提出方法在投产使用后能发挥预期成效。

