小学数学技能教学要关注理解
叶明珠
摘 要:学生对破损量角器的使用不知所措,引发了教师对技能教学的思考,即数学技能教学要用理解代替机械、重复的训练。文章以“角的度量”为例,探索挖掘技能教学本质、促进概念深入理解的策略。
关键词:小学数学;技能教学;关注理解
一、问题的缘起
数学家华罗庚曾说,数起源于数,量起源于量。“角的度量”单元安排在人教版《义务教育教科书·数学》四年级上册,该单元主要包括“线段、直线、射线”“角”“角的度量”“角的分类”“画角”这五部分内容。学生在认识了射线和角的概念的基础上学习用量角器这一度量角的工具进行测量。课堂上,通过笔者的讲解,学生模仿和反复练习后已经熟练掌握了量角器的使用方法。然而,一道稍有变化的测量问题却暴露了学生对知识理解和掌握的真实情况。
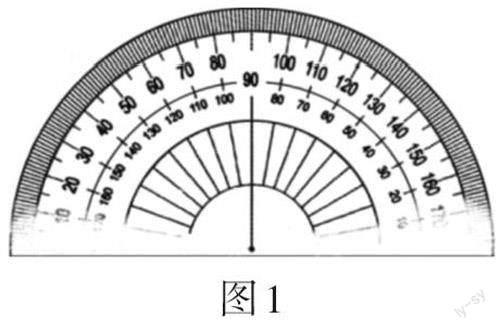
师:如图1,有一个0刻度线磨损了的量角器,你能用它测量角的度数吗?
很多学生的答案是:不能。
為什么学生面对稍有变化的测量问题时会束手无策呢?在知识学习之后,笔者带领学生回到知识学习之初寻找原因。在日常教学中,技能教学往往是教师讲解示范,学生模仿操作,并进行强化训练。机械的模仿操作容易降低学生的思维水平,因为在操作中缺少思考与探究,更缺少猜想与创造。学生表面的熟练并不代表对量角原理的真正理解。
有人可能认为,只是一个量角工具的使用,直接告知学生再练习使用为什么不行?会有那么大的影响吗?试想如果学生理解了量角器量角的原理,就会想到上述习题可以利用量角器中间完好的部分进行测量。要做到这一点,就要对量角器的使用这一简单技能背后隐藏的角的概念和原理深入理解。如果只是单纯地模仿教师的测量方法,熟记测量步骤,或者进行反复的测量练习,对这类非常规的灵活题目是很难做到变通的。
二、促进学生理解量角器量角
如何让学生灵活运用数学技能呢?有效的办法就是让学生理解为什么这么做。在进行这一技能教学之前,教师先要明确“角的度量”一课的教学难点是什么,用量角器量角的本质是什么,它对角的概念的理解有何补充作用,学生在学习这节课之前已有哪些经验,怎样促进正迁移、弱化负迁移。结合以上思考,笔者从以下三个方面促进学生对量角器量角这一技能的理解。
1. 尊重学生已有经验,找准教学起点
通过以往的教学观察,笔者从学生的课前调查、课中诊断、课后练习中发现,受长度测量的影响,很多学生习惯“一端对齐,从头量起”。在这种思维定式下,如果哪种测量不是“从头开始”,学生就会遇到困难。
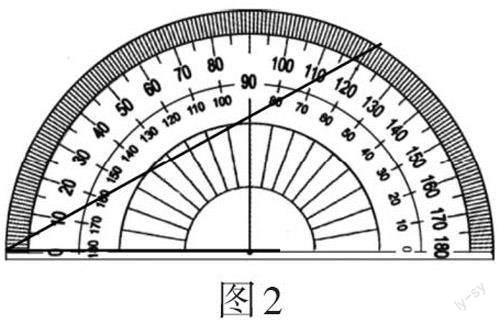
教师要尊重学生的已有经验。教学前,笔者让学生先试先量,充分暴露学生的思维过程,肯定学生勇于尝试的精神。在学生尝试的过程中,笔者细心观察、发现、展示学生的量法(如图2),并提问:能想到用量角器上的角与所量的角进行重合比较,思路非常好,这种敢于尝试的精神值得表扬。我们一起来找找,在量角器的一端能找到角吗?在肯定了学生的思路之后,笔者有意识地帮助学生排除“从头量起”的这种负迁移,鼓励学生辨析,在交流中发现量角器的一端的一条边是曲线,不具备角的特征。笔者追问:仔细观察手中的量角器,在哪里才能找到角呢?把你的发现与同桌说一说。笔者引导学生探索以中心点为顶点的角的存在,逐步从不规范的测量方法一步步接近,直至达到科学的度量。
2. 明确量角器量角的本质,为学生探究搭好脚手架
“角的度量”一课的第一环节“下面两个角哪个大些?大多少?”已经为“用重合法比大小”作了铺垫,旨在引导学生了解用量角器测量角的本质就是将量角器上的角与测量角进行“重合”比较。学生拿到量角器后,会发现中心点、0°刻度线、两圈刻度,却往往看不到上面隐藏的各种大小的角。理解了测量本质,笔者要做的就是引导学生找到量角器上隐藏的角。笔者曾经听过华应龙老师执教的“角的认识”,印象最深的莫过于让学生在打印好量角器的纸上画出各种度数的角,从而发现这些隐藏的角。“画角”的教学在教材中安排在“角的度量”和“角的分类”之后,华老师就是因为对量角器量角的本质把握准确,创造性地使用教材,让教材为其所用,先“画角”再“量角”,教学效果非常好。学生熟练找到量角器上各种度数的隐藏角,就可以与测量角进行“重合”比较了,量角就变得非常容易了。
反之,如果只是按照教材步骤:把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数。这种总结出来的“两合一看”(0°刻度线在左边看外圈,0°刻度线在右边看内圈)学生不深入了解可能一头雾水。如果把方法的探究变成了学生的机械模仿,学生只知其然,却不知其所以然,久而久之会使学生缺乏数学思考能力,更不要说灵活应用了。
3. 丰富技能教学内涵,在探索中深化对概念的理解
有人说,“角的度量”一课除了教学生使用量角器,还能教什么?笔者认为是“追求理解”,理解量角器的构造、理解角的度量的本质,进一步理解角的概念。只有注重理解,才能将机械的模仿转化为有意义的操作。
角的概念的定义为:从一点引出两条射线所组成的图形叫作角。角的两条边为什么是射线,而不是线段呢?虽然在课堂上并没有学生提出这个疑惑,似乎教材这么规定就这么规定吧,教师也没想过要对这个问题作出解释,学生对教材的概念规定默认接受,但是对于它的内涵却是不知。而“角的度量”一课刚好可以对这一概念进一步解惑,丰富学生对角的概念内涵的理解。
课后“做一做”第2题:量出下面两个角的度数,并比较它们的大小(图略)。你发现了什么?两个角边的长度不同,通过测量,学生发现两个角都是45°,说明角的大小与两边的长短无关,只与两边张口的大小有关。正是因为角的两条边是射线,任意延长却不影响角的大小,所以在遇到角两边画得太短不方便用量角器测量时,可以根据射线的性质将射线向一边延长,便于在量角器上观察角度。
教师要尊重学生原有的认知经验,让学生先试先量,充分暴露学生的思维过程,这样才能准确把握教学起点,通过引导发现,消减已有经验对新知造成的负迁移,排除干扰。同时,教师要研读教学参考书,找准教学难点,揭示问题的本质,找到突破难点的方法,为学生探究搭好脚手架,降低学生的理解难度,缓解学生的畏难情绪。在探索和经历中丰富技能教学的内涵,深化对概念类知识的理解。
三、结束语
数学技能要在理解的基础上方能灵活运用。背出来的东西,遇上“活”题就束手无策了,能理解、有联系、有意义的记忆才可能解决不断变化的问题,有思维含量的记忆才可能持续发挥作用。在小学阶段,技能教学不是只有角的度量,公式、计算法则、口诀等都是学生探索发现的载体,经历一连串“为什么”的探究过程,数学思想将始终伴随着学生。只要教师用心思考,就会让这些题材发挥它最大的教育价值,技能教学也有别样精彩。
参考文献:
[1]华应龙. 我这样教数学:华应龙课堂实录[M].武汉:长江文艺出版社,2020.
[2]李方方. 关于数学技能教学的几点思考[J]. 小学数学教育,2019(23).
[3]胡彬彬. 谈小学生数学技能的培养策略[J]. 黑河教育,2018(10).

