“宏”观一道题，“微”观数学哲理

戴晶晶

［摘  要］ 通过“宏”观一道题，“微”观数学哲理，研究者对特级教师张宏伟的“割铁皮”一课进行记录和赏析：通过题组对比，让学生感悟真理不是永远都对；通过研透问题，让学生感悟方法比知识更重要；通过一题多变，让学生感悟探究的永无止境。

［关键词］ 全景教育；数学哲理；割铁皮

在“当代教育大讲堂·渝州之秋”小学数学教学研讨会上，特级教师张宏伟执教的“割铁皮”（人教版三年级下册）一课，笔者印象深刻，颇为喜欢。

在教学过程中，张老师借助“割铁皮”的游戏，和学生做个铁皮匠，玩剪铁皮。他通过“从1张長方形铁皮上剪掉1张边长5米的正方形铁片后，求剩下铁皮的面积和周长”这一道题，变化题目中的信息，引导学生找到计算剩下铁皮的面积和周长的方法，感悟遇到不确定的信息时要想出所有的可能。整节课上张老师丰富的“表情包”、幽默的话语激活了学生的数学思维，让他们敢于挑战、不怕失败、超越自我，畅游在美妙的数学世界里。

一、题组对比，感悟真理不是永远都对

出示题目：1张长方形铁皮，长20米，宽15米，从它身上剪掉1块边长5米的正方形铁片后，问题（1）剩下的铁皮的面积是多少平方米？问题（2）剩下的铁皮的周长是多少米？

师：我先找1位同学把题目读一遍，听完题目，大家开始做题。

学生独立完成，教师巡视了解学生的解题情况。

师：通过巡查，老师发现大家第1题都做对了。

板书：第一题：20×15－5×5=275（平方米）；第2题：（20＋15）×2－5×4=50（米）……

学数学最重要的是学思维，我们不仅要学会自己思考，还要读懂别人是如何思考的。（指着板书）我们来看看黑板上这两道算式，一起来看看里面有什么样的解题思路，同时看看第2题的解题思路是否正确呢？

生1：第1题的解题思路是用原来的铁皮面积减去被剪掉的正方形铁皮面积等于剩下铁皮的面积。

师：（指着第2个算式）这道算式又有怎样的解题思路呢？

生2：先求出原来的周长，再减去被剪掉的正方形铁皮的周长，等于剩下铁皮的周长。

师：根据板书内容，这两个算式有一个共同的地方，是什么？

生2：都是用原来的减去剪掉的等于剩下的。

师：很好，前面两位同学准确地说出了两道算式的解题思路，接下来我们看看这两道题的解题思路正确吗？

学生纷纷作答，最终一致认为第1题的思路正确，第2题的思路错误。

师：第2题究竟该怎么作答呢？

生3：（学生画图）通过图片可以得出，剪掉1个正方形铁片后，剩下的是1个凹进去两条边的不规则图形，我们把这两条凹进去的边平移出来，图形又变回了原来的长方形。所以，剪掉1个正方形铁片后，原来铁片的周长不变，它只是面积减少了。

其他同学纷纷点头，同意生3的观点。

赏析：德国数学家克莱因说：“数学是一种理性的精神，使人类的思维得以运用到最完善的程度。”追求真理是人类永恒的目标，人们为了证明数学真理，不仅要回答“什么是数学真理”，还要回答“为什么它是数学真理”。张老师精选了1道周长和面积的对比题，巧妙地引发学生的认知冲突，在呈现学生的算式和解题思路后总结出两种方法的共性：原来的减去剪掉的等于剩下的。面对这个一年级学生就开始接触的真理，有的学生慢慢发现这个真理在计算剩下铁皮的周长时不适用了，他们迫切地借助画图策略寻找正确答案。此时，张老师趁热打铁，告诉学生不能自以为是地认为真理在任何地方永远都对，对待每一个数学问题都要重新思考，培养他们的批判性思维。

二、研透问题，感悟方法比知识更重要

1. 感悟“画图”方法

师：在学习数学的时候，如果无法通过语言描述准确理清题意，我们可以借助图形，画图是我们思考和解决数学问题很重要的一个路径。在解决切铁皮这道问题的过程中，聪明的同学把原来的图和剪掉后的图都画出来，通过对图片的分析，答案就一目了然了。“画图法”是解决数学问题的一个很有用的方法，习得一些有用的解题方法，可以给你的学习锦上添花。

师：请大家观察图片（图1），其实这个画图还不完美，你们想想是为什么？

生4：没有标数据。

师：（给每条边标上数据）标上数据后，老师觉得这个图形还不够完美，因为每条边还没有自己的称呼，我们只能说“这条边”“那条边”，这样表述一点也不清楚，所以我们还应该做什么？

生5：给每条边标上序号。

师：（给每条边标上序号）现在，这个图形就完美了！

图1

2. 感悟“分类”思想

师：我们继续来分析例题，针对周长问题，大家都对生3的解题思路表示赞同。但老师想说，这道题如果满分是10分，生3的回答只能得到3.33分。

全班学生都面面相觑，生4的思路明明是正确的，为什么不能得满分呢？

师：张老师送你们一句话——听过不如看过，看过不如做过，做过不如错过。做错了，这道题才有研究价值，你们知道刚才生3的解题思路为什么没得满分吗？

生6：它没有固定……（教师示意学生不要往下说了）

师：你很了不起，举手不说出来是对你同伴最大的尊重，你尊重他思考的时间和空间。我们的审题出了问题，其实题目中有确定的信息和不确定的信息，我们来细品题目中哪一句话是确定的，哪一句话是不确定的？

……

师：“从它身上剪掉1块边长5米的正方形铁片”这句话有争议了，你觉得什么是确定的，什么是不确定的？

生7：它的边长、面积和周长是确定的，但是减去铁皮的位置是不确定的，剪边长5米的正方形铁皮有无数种不同的方法。

师：你是一个伟大的哲学家，握握手。数学上处理无数种方法的方法就是分类，解题时我们需要想出所有的可能。那在铁皮上减去1个正方形，可以有几种剪法呢？

生8：可以在4个角上剪、在边上剪、在正中间剪。

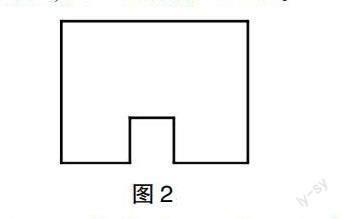
师：（出示“从边上剪”，见图2）剪去之后我们要比较变化前和变化后的周长，找一找有什么关系。

生9：和原来周长相比，“枪毙”了1个5米，“生出”了3个5米，多了2个5米，所以变化后的周长比原周长多了10米，周长变成了80米。

师：（出示“在中间剪”，见图3）请大家看看这个图形的周长和原来图形的周长一样吗？

生10：原来图形周长没有被“枪毙”，反而“生出”了4个5米，周长就多了20米，所以变化后的周长是90米。

赏析：数学家华罗庚说：“新的数学方法和概念，常常比解决数学问题本身更重要。”《义务教育小学数学新课标（2022年版）》在总体目标中明确指出：“学生能够获得适应未来社会生活和进一步发展所必需的重要数学知识以及基本的数学思想方法和必要的应用技能。”这一总体目标贯穿小学整个学习过程，这充分说明了数学思想方法的重要性。智慧的张老师通过深入挖掘1道周长题目的数学内涵，教会学生画图的方法，不仅要标上每条边的数据和序号，还要比较变化前后图形周长的不同，这个数学方法将贯穿整节课和“空间与图形”领域的学习过程。同时，张老师还在题目中设置了“陷阱”，让学生经历先入“坑”再出“坑”的全过程，深刻体会遇到不确定信息要进行分类讨论，尽可能想出所有可能。

三、一题多变，感悟探究是永无止境的

师：太牛了，孩子们！上完这节课之后，你和以前相比有哪些收获或者不一样了？

生11：以前我們都是用很老土、很死板的方法做题，现在我们掌握了新方法，感觉比以前更厉害了。

生12：遇到问题要多思考，不能用以往的经验去解决所有问题。

生13：我们做题时要先观察它什么是确定的，什么是不确定的；找到不确定的把它分类，再进行比较。

师：今天你们都非常牛，学这些方法可以让你们一生受用。老师在下课前给你们一个猜想：1张长方形铁皮，长20米，宽15米，从它身上剪掉一块边长a米的正方形铁片后，剩下的铁皮的周长是多少米？如果在角上剪，剩下的周长变了吗？

全班学生都说“没变”。

师：如果在边上剪，剩下的周长增加多少？

全班学生都说“2个a”。

师：如果在中间剪，剩下的周长增加多少？

全班学生都说“4个a”。

师：全军覆没，没有一个全对。因为它是未知数a，所以结果就不一样了。如果a和长方形的宽相等会怎样？请大家回家研究研究！

……

赏析：俗话说“活到老，学到老”。张老师用一道题为载体，引导学生在思考中揭示周长和面积的数学本质，培养学生具体问题具体分析的能力，提升学生解决实际问题的数学素养。在课末，张老师一题多变，仅改变了题目中的一个数学信息，这时全班学生就入“坑”了。张老师故意只给了小提示，留给学生到课后研究这道题，进而出“坑”，打通了课堂和课后的数学学习时空，让他们感受到数学探究是永无止境的。

综上所述，小学数学教师在课堂上要像张老师那样充分利用一道题目的价值，不断改变一道题目中的关键字眼或者条件，让学生在不断辨析中深刻且灵活地理解周长的计算方法，感受数学学习能解决生活中的实际问题，感受数学的应用价值。