基于SMES-SAPF的无源动态演化和滑模控制策略

齐国庆,周建萍,茅大钧,从帆平,黄祖繁

(上海电力大学自动化工程学院,上海市200090)

0 引 言

近年来,由于大量电力电子设备投入使用,使得电力系统中电能质量下降;同时,配电系统的负载端也呈现多样化的趋势,除了常见的线性负载外,非线性负载、不平衡负载、脉冲负载等先进的电气设备接入配电系统[1],造成系统中电流波形畸变,无功功率损耗增加等谐波污染问题日趋严重,如何提高电能质量是现代配电系统需要解决的重要问题之一[2-5]。

在众多谐波抑制工具中,并联有源电力滤波器(shunt active power filter,SAPF)因其具有响应速度快、可控性高、耐压优良、能够实现动态补偿等特点,在解决谐波污染问题中被广泛应用和研究。控制策略的选择会直接影响SAPF的补偿性能,传统的控制策略包括比例积分(proportional integral, PI)控制,比例谐振(proportional resonance,PR)控制、重复控制等控制策略[6]。PI控制是一种方法简单、响应迅速的线性控制策略,但存在高超调、鲁棒性差的问题,不适用于运行状态多变的非线性系统。而无源控制是一种根据系统结构特性,从能量角度对系统进行控制的非线性控制策略,目前是非线性系统研究的热点[7-8],但其自身存在无法适应参数变化和抗干扰能力差的缺点。为此文献[9]将非奇异终端滑模控制与无源控制相结合,不仅增强了系统的抗干扰能力,同时也解决了终端滑模控制存在的固有奇异性问题,有效提升了SAPF的补偿性能,但滑模控制的抖振问题仍然无法避免。文献[10]提出了一种基于动态演化控制(dynamic evolution control, DEC)的非线性控制策略,该控制策略能够迫使三相补偿电流误差经过特定的演化路径进行演化,从而实现控制系统的误差以指数形式趋于零的状态,且不存在抖振。可见,动态演化控制能更好地弥补无源控制的缺点。

除了改进控制策略外,配电系统还可以通过在系统外部增加储能设备来增强稳定性。目前,研究较为广泛的储能装置有电池储能(battery energy storage,BES)、超级电容储能(super capacitor energy storage,SCES)和超导磁储能(superconducting magnetic energy storage,SMES)几类[11-13]。然而,电池储能应用在运行状态多变的电力系统中会造成电池频繁的充放电,影响电池的使用寿命[14];超级电容储能中对串联电容器的电压协同控制一直以来是一个需要解决的难题[15];相较于上述两种储能装置,SMES具有响应速度快、抗干扰能力强、循环次数多等优点,在抑制系统振荡失稳和保证系统安全稳定运行方面有广阔的应用前景[16-18]。文献[19]将SMES应用于模块化多电平换流器的柔性直流输电(modular multilevel converter based high voltage direct current, MMC-HVDC)系统中,有效抑制了系统直流振荡,提高了系统的稳定性。文献[20]设计了一种由模块化多电平换流器(modular multilevel converter, MMC)和新型斩波器构成的SMES系统拓扑结构,多个超导磁体共同作用提升了系统的储能容量。文献[21]在光伏并网发电系统中引入超导磁储能限流器(superconducting magnetic energy storage-fault current limiter,SMES-FCL),不仅使系统具有限流和储能的双重作用,还可以有效地提升光伏并网发电系统的故障穿越能力。

综上所述,SMES所具有的抑制振荡和增强稳定性的能力能很好地弥补有源电力滤波器抗干扰能力弱的缺点。为此,本文针对超导磁储能型有源电力滤波器(SMES-SAPF)在谐波治理方面的应用进行了研究。首先,基于SMES-SAPF的数学模型设计了一种基于欧拉-拉格朗日(Euler-Lagrange, EL)模型的无源动态演化控制器,该控制器可强制无源控制率中的误差信号执行特定的动态演化路径,迫使误差快速趋于零;其次,根据直流侧斩波器的数学模型设计了滑模控制(sliding mode control, SMC)器,并采用饱和函数抑制滑模控制所固有的高频抖振。最后,通过MATLAB/Simulink建立仿真模型,在不同负载接入的情况下验证了所提控制策略的有效性与可行性。

1 SMES-SAPF的数学模型

基于超导磁储能型有源电力滤波器的拓扑结构如图1所示,主要由网侧电源、交流侧有源电力滤波器SAPF、直流侧斩波器和负载四部分构成。其中L0、L1为线路滤波电感,R0、R1为线路等效电阻,C为直流侧电容,Usa、Usb、Usc为三相网侧电压,isa、isb、isc为三相网侧电流,ila、ilb、ilc为负载支路电流,ifa、ifb、ifc为补偿电流,Uca、Ucb、Ucc为逆变侧输出电压,Udc为直流侧电容电压,R2为非线性负载电阻,L2为非线性负载电感,L3为不平衡负载,L4为脉冲负载,T为脉冲周期,D0为脉冲负载占空比,Lsc为超导磁体,isc为流经超导磁体的电流,D1、D2为续流二极管,V1—V8为IGBT功率器件。

图1 SMES-SAPF拓扑结构Fig.1 SMES-SAPF topology

根据其拓扑结构,可以得到SMES-SAPF在三相静止坐标系下的数学模型:

(1)

(2)

式中:三相输出电压Uci满足:

Uci=SiUdc(i=a,b,c)

(3)

定义开关函数Si为:

(4)

将式(1)、式(2)变换到dq坐标下可得:

(5)

(6)

式中:ifd、ifd分别为补偿电流dq轴分量;ω为角速度;Usd、Usd分别为网侧电流dq轴分量;Sd、Sd分别为开关函数dq轴分量;Ucd、Ucq分别为逆变侧输出电压dq轴分量。

选取系统状态变量为:

(7)

将式(5)改写为dq坐标系下的EL模型:

(8)

式中:M为各项储能元件的惯性矩阵;J为系统内部耦合关系的反对称矩阵;R为内部耗散性器件的对称正定矩阵;u为反映系统内外能量交互的控制变量。各矩阵表达式为:

(9)

2 SMES-SAPF的控制策略

2.1 SMES-SAPF数学模型无源性分析

假设一个多输入多输出的系统:

(10)

式中:v为n阶状态变量,v∈Rn;u为m阶输入矢量,u∈Rm;y为系统m阶输出矢量,y∈Rm,且y关于x连续;f(·)为关于(v,u)的局部Lipschitz函数[22];h(·)为y的等价函数。

系统严格无源定义:若系统存在能量存储函数H(x),该函数为连续可微且半正定,若存在正定函数G(x),对于任意T>0,此时系统的输入u、输出y及能量供给率uTy满足式(11),则系统是严格无源的[5]。

(11)

对于式(8)所示的EL模型,选取能量存储函数为:

(12)

对式(12)求导可得:

(13)

令

(14)

显然满足式(11),此时可理解为:由于R为正定矩阵,则xTRx大于零,所以能量存储函数H(x)的导数必然是小于供给率uTy,即外部能量供给率大于系统自身能量存储率,系统在运行时存在能量损耗,符合无源性定义,表明系统是严格无源的。

2.2 无源控制器设计

设状态变量参考值为:

(15)

参考式(8)可得状态变量参考值的EL模型为:

(16)

式中:上标“*”代表对应变量的参考值。

令状态变量误差为:

xe=x-x*

(17)

将式(8)与式(16)相减可得系统误差EL模型为:

(18)

选取能量存储函数为:

(19)

假设t为系统运行时间,当t趋于无穷时,此时状态变量x无限接近参考值x*,误差存储函数H(xe)将收敛到0,实现了无源控制,即

(20)

此时的误差EL模型可等效为:

(21)

对式(19)求导后将式(21)代入可得:

(22)

Rdxe=(R+Rz)xe

(23)

式中:Rd为系统整体阻尼矩阵;Rz为阻尼矩阵,且满足:

(24)

式中:Rz1、Rz2分别为阻尼项。

将式(23)代入式(18)可得注入阻尼后的误差EL模型:

(25)

将Jxe移项,令式(25)左侧等于零整理可得系统无源控制率:

(26)

展开式(26)得:

(27)

2.3 无源动态演化控制器设计

由于不同负载的接入,如不平衡负载、脉冲负载等,在SMES-SAPF系统中会不可避免地出现高误差信号,进而导致控制器的控制精度大幅度下降,因此,本文采用一种动态演化理论控制策略更好地调节误差。

动态演化理论控制是一种非线性控制策略,该方法适用于调节输出信号的误差,其基本思想是强制误差信号执行一个特定函数规定的路径,即动态演化路径,迫使误差信号按照演化路径进行演化,从而获得一个快速零误差的状态[23-24]。

定义Y为系统的误差状态函数;Y0为Y的初始值,l为设计参数(即演化速率),选择指数函数作为演化路径,即

Y=Y0e-lt

(28)

对式(28)求导可得动态演化函数为:

(29)

设系统变量误差为xerr,将式(29)改写为:

(30)

式中:xerr、Y满足:

(31)

式中:xref为变量参考值;x为变量实际值;ε为非零系数。式(30)为动态演化理论控制的广义表达式,通过设置合适的参数值(l和ε),可以使补偿电压以指数级下降的方式趋于零。

定义补偿电流误差dq轴分量为ifde、ifqe,满足:

(32)

将式(32)代入式(30),即将补偿电流实际值dq轴分量ifd、ifq按式(30)规定的动态演化路径进行演化,由此可得:

(33)

式中:ifdD、ifqD为经演化路径演化后的实际值。将式(33)代入式(27)可得控制率为:

(34)

控制率Ucd、Ucq满足:

(35)

即开关函数为

(36)

由上式可知,控制率受直流侧电压Udc的直接影响,保证直流端电压的稳定是系统能稳定运行的关键。因此,下文将针对直流侧斩波器进行控制器设计。

2.4 直流侧斩波器滑模控制(SMC)器设计

SMES-SAPF直流侧电容C经斩波器与超导磁体Lsc相连,通过控制全控开关V7、V8的导通和关断实现超导磁体的充放电。斩波器有三种工作状态,如图2所示,根据不同的开关组合可分为充电状态、放电状态和续流状态。

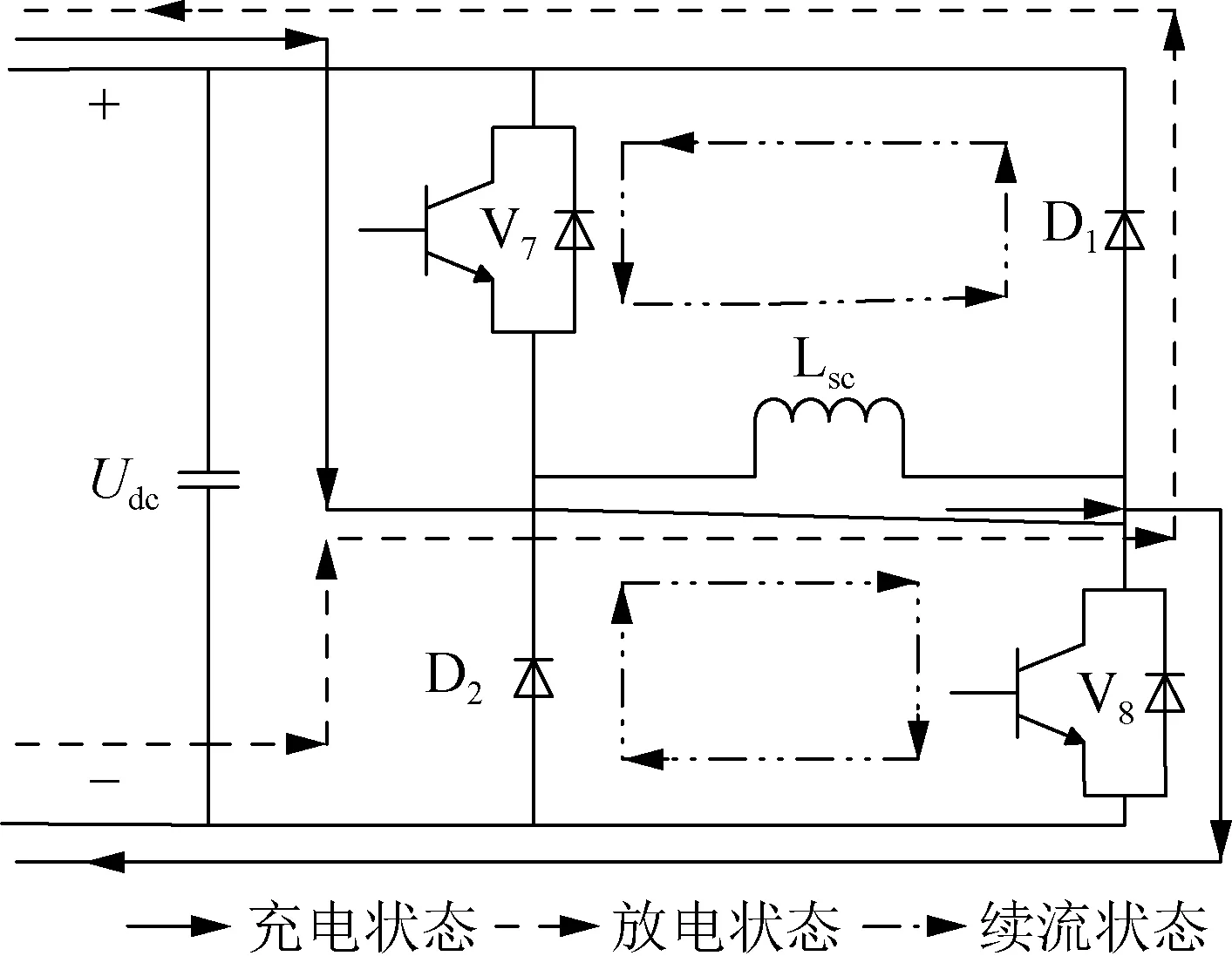
图2 直流侧斩波器拓扑结构及运行状态Fig.2 DC side chopper topology and operation status

续流状态:开关V7导通,V8关断(或V7关断,V8导通),此时流经超导磁体的电流isc在V7与D1(或V8与D2)构成的回路循环流通,即超导磁体与直流端电容之间无能量交互。

充电状态:开关V7、V8均导通,此时直流侧电容对超导磁体进行充电,且直流侧电压Udc与流经超导磁体电流isc满足:

(37)

式中:ton为开关V7、V8导通时间;Lsc为超导磁体电感。

放电状态:开关V7、V8均关断,此时超导磁体对直流侧电容进行放电,且直流侧电压Udc与流经超导磁体电流isc满足:

(38)

式中:toff为开关V7、V8关断时间。

联立式(37)和式(38)可得占空比D、Udc、isc三者之间满足:

(39)

当D∈(0,0.5)时,磁体处于放电状态;当D为0.5时,磁体处于续流状态;当D∈(0.5,1)时,磁体处于充电状态。

不同负载的接入会造成直流端电压产生超调,且短时间内无法恢复稳定,单纯靠PI控制鲁棒性较差,因此,本文引入滑模变结构控制用于消除SMES-SAPF系统中不同负载接入对直流侧电压的影响。

(40)

选取积分滑模面为:

(41)

式中:k1、k2为滑模面控制系数。

选取指数趋近率为:

(42)

式中:c1、c2为趋近率系数,趋近率中采用sat饱和函数削弱滑模控制自身的高频抖振问题,其中饱和函数需满足:

(43)

对式(41)求导后联立式(42)、(40)可得:

(44)

将式(39)代入式(44)可得斩波器占空比表达式为:

(45)

综上,SMES-SAPF直流侧斩波器滑模控制框图见图3。

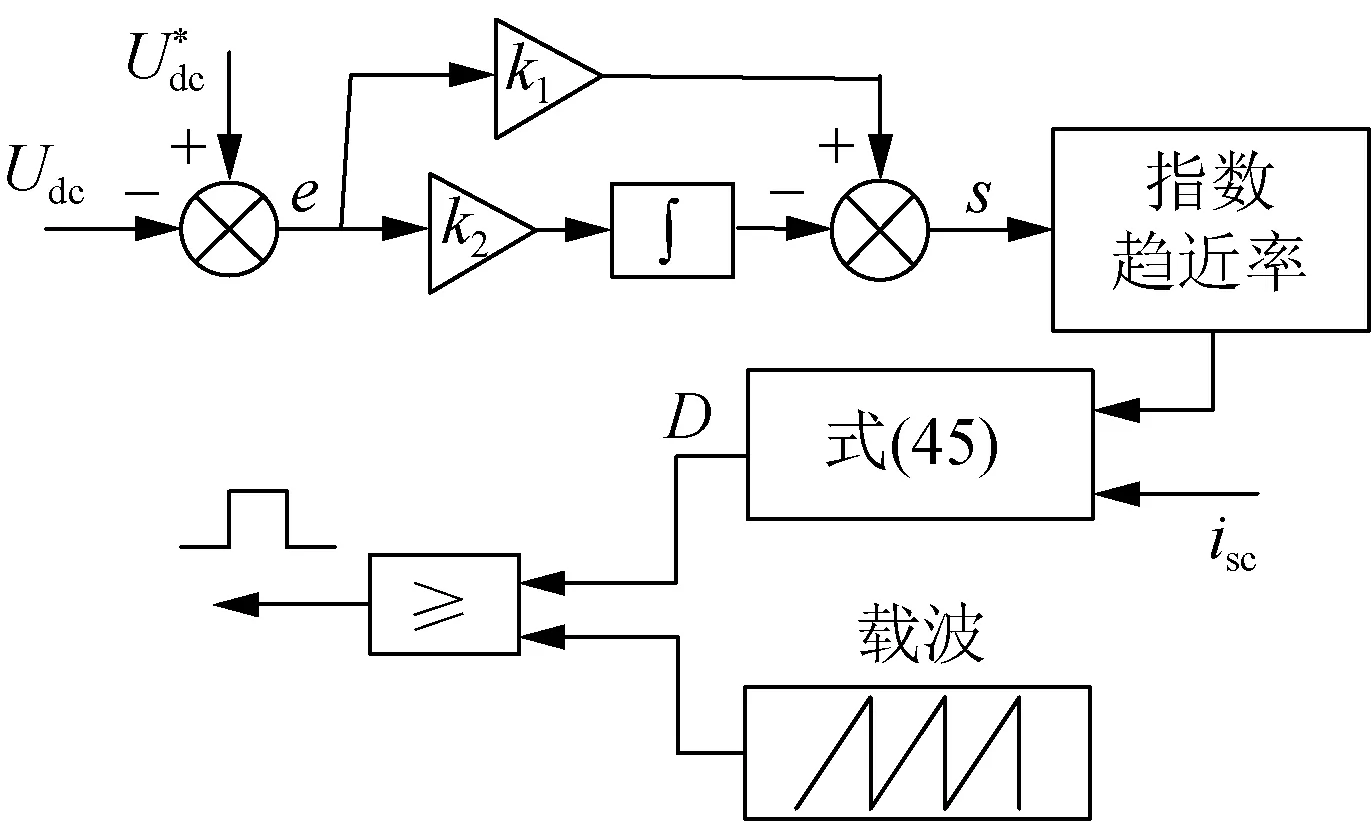
图3 SMES-SAPF直流侧斩波器滑模控制框图Fig.3 SMES-SAPF DC side chopper sliding mode control block diagram

利用Lyapunov稳定性判据对上述滑模面的合理性进行判定,选取Lyapunov函数为:

(46)

对式(46)求导可得:

(47)

显然式(47)为关于s的等式,当e等于0时,此时系统稳定;当e不等于0时,即s不等于0,此时系统为非稳定状态,而由Lyapunov稳定性判据可知,只要保证上式小于0即可将e在有限时间内收敛到零,故控制参数需满足c1、c2、k1、k2都大于0便可保持系统稳定。

3 SMES-SAPF的控制系统

根据上述分析,设计SMES-SAPF的控制框图,如图4所示,由图可知,该控制系统主要由内环控制器和外环控制器两部分构成,其中内环控制器包括正负序电流提取、无源动态演化控制和调制模块等。具体控制过程如下:首先,负载电流il,abc经正负序分离后,通过低通滤波器输出补偿电流在dq坐标系下的参考值;然后补偿电流与参考值经式(33)进行无源动态演化控制;最后将得到的控制率通过空间矢量脉宽调制输出开关驱动信号。而外环控制器包括滑模控制和调制模块,控制过程为:直流侧电压与参考值经式(45)进行滑模控制,输出的占空比通过脉宽调制得到驱动信号驱动直流侧斩波器工作。

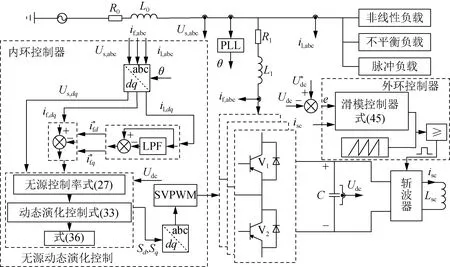
图4 SMES-SAPF的控制系统Fig.4 Control system of SMES-SAPF

4 仿真分析

为了验证超导磁储能型有源电力滤波器(SMES-SAPF)的谐波治理能力以及所提无源动态演化控制策略的优越性,在MATLAB/Simulink平台搭建仿真模型,针对系统搭载非线性负载、不平衡负载、高频脉冲负载三种负载及其他运行状态分别进行仿真实验对比,实验参数见表1。

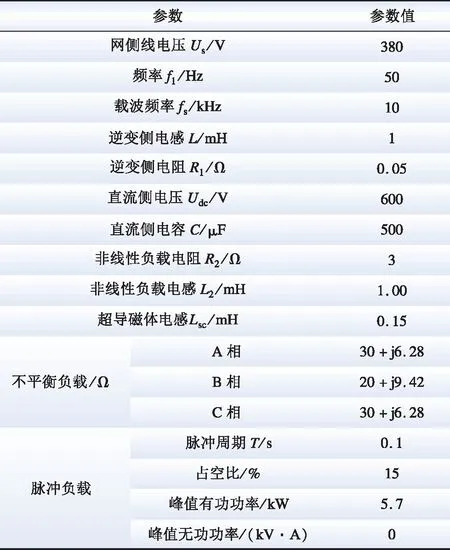
表1 实验参数Table 1 Experimental parameters

4.1 算例1

该算例旨在探究SMES-SAPF整体系统的谐波治理能力,测试负载端在搭载不同负载情况下谐波对系统的影响。设置仿真时间为1.20 s,其中在0.25 s时控制器开始工作,在0～0.35 s期间负载端接入非线性负载;0.35～0.50 s期间非线性负载发生突变,突变电阻为10 Ω;0.60～0.80 s期间不平衡负载接入;0.90～1.20 s期间脉冲负载接入,SMES-SAPF分别采用无源控制以及本文所提控制策略,仿真结果如图5—8所示。

图5 SMES-SAPF非线性负载仿真波形Fig.5 Nonlinear load of SMES-SAPF simulation waveform

由图5可知,系统负载端搭载非线性负载时,由于0.25 s之前控制器未投入工作,网侧电流谐波含量较高,整体波形呈非对称非正弦状态;0.25 s时控制器开始工作,对比图5(a)和图5(b)可知,使用无源控制的系统虽然可以将网侧电流补偿为正弦波形,但在控制器工作和负载突变的瞬间超调明显,约0.04 s之后整体趋于稳定,且波形略有畸变,正弦程度较差;而使用无源动态演化控制的系统网侧电流无超调,负载突变后电流波形仍能保持平滑稳定,可见SMES-SAPF系统在无源动态演化控制能更好地补偿因非线性负载造成的谐波问题。

0.60 s时负载端接入不平衡负载,对比图6(a)和图6(b)可知,使用无源控制的系统网侧三相电流明显不平衡,不平衡度高达7.13%;而使用无源动态演化控制的系统网侧三相电流不平衡程度较小,不平衡度仅为1.43%,因此,当系统运行在不平衡负载情况下,SMES-SAPF系统在无源动态演化控制下补偿效果更好。

图6 SMES-SAPF不平衡负载仿真波形Fig.6 Unbalanced load of SMES-SAPF simulation waveform

0.90 s时负载端接入脉冲负载,脉冲周期0.10 s,脉冲占空比为15%,对比图7(a)和图7(b)可知,使用无源控制的系统网侧电流受脉冲负载影响较大,波形失真程度较大,电流脉动处幅值高达240 A,短时间突然升高的电流必然会对系统的安全运行产生影响,显然无源控制无法有效治理该负载造成的谐波问题。而使用无源动态演化控制的系统网侧电流失真程度较小,电流波形脉动处幅值变化较小,基本可实现持续稳定运行,即SMES-SAPF系统在无源动态演化控制下能有效地解决脉冲负载造成波形脉动以及谐波污染问题。

图7 SMES-SAPF脉冲负载仿真波形Fig.7 Pulse load of SMES-SAPF simulation waveform

图8为PI控制和所提控制策略下SMES-SAPF的仿真波形。由图8(a)可得,在PI控制下0.25 s控制器开始工作时有明显电流跌落,0.04 s后趋于稳定,当负载端接入脉冲负载时,网侧电流出现较大波动;而无源动态演化控制策略波形平滑,0.25 s处无电流跌落,且脉冲负载接入情况下电流波动小,即本文所提控制策略抗扰动能力更强、补偿效果更好。

图8 不同控制策略下SMES-SAPF的仿真波形Fig.8 Simulation waveform of SMES-SAPF under different control strategies

不同控制策略下的电流性能如表2所示,由表2可知,对比PI控制和无源控制,不管是网侧电流的总谐波畸变率(total harmonic distortion,THD)、不平衡度还是跃变幅值,SMES-SAPF在无源动态演化的控制下,网侧电流谐波含量更少,波动更小,波形更加平稳,整体谐波治理能力远远优于PI控制和无源控制。

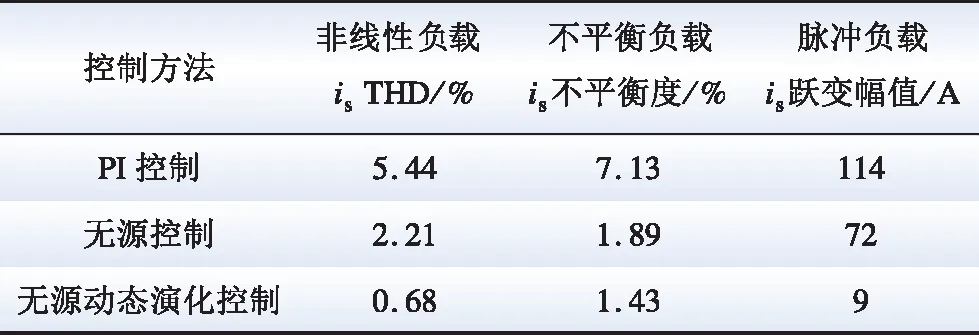
表2 不同控制策略下网侧电流is性能Table 2 Grid current is performance under different control strategies

4.2 算例2

算例2探究系统在不同状态下直流侧电压的运行情况,主要验证在不同控制策略情况下,通过对比SAPF直流侧电压稳压情况,突出SMES-SAPF系统直流侧斩波器采用滑模控制的有效性。设置直流侧参考电压为600 V,仿真时长1.50 s,0～1.20 s之间各负载接入参考算例1,此处不再赘述,1.20 s时直流侧参考电压增大到620 V,1.35 s时减小为600 V,仿真结果如图9所示。

图9 不同状态下直流电压仿真波形Fig.9 DC voltage simulation waveforms in different states

如图9(a)所示,当负载端搭载非线性负载时,使用SAPF和使用SMES-SAPF的系统基本均可实现直流侧电压的稳定,但SAPF系统不管采用PI 控制还是滑模PI控制,直流侧电压距参考值600 V均有一定误差,其中滑模PI控制下误差相对较小;而采用滑模控制的SMES-SAPF系统能准确跟踪参考值,且上下振幅较小。在0.35 s负载突变时,SAPF直流侧电压有明显超调,在PI控制下0.04 s后电压趋于稳定,稳定后的电压偏离参考值3.5 V,在滑模PI控制下0.05 s后电压才能趋于稳定;而采用滑模控制的SMES-SAPF系统几乎不受负载突变的影响,直流侧电压无超调,仍能准确跟踪参考值且保持稳定。

当系统搭载不平衡负载时,仿真结果见图9(b),负载接入的瞬间,SAPF系统直流侧电压有明显的电压跌落,跌落电压高达16 V,0.03 s后电压趋于稳定,但稳定后电压振幅较大,采用PI 控制上下振幅区间为593.5～604.4 V,采用滑模PI控制上下振幅区间为594.8～604.0 V;而SMES-SAPF系统在负载接入时无电压跌落,在0.60～0.63 s期间直流侧电压有小幅度畸变,随后恢复稳定状态,上下振幅区间仅为598.6～601.4 V,几乎不受不平衡负载接入的影响。当0.9 s系统接入脉冲负载时,仿真结果见图9(c),在每次的脉动处,SAPF系统直流侧电压也会随之产生高幅振荡,采用PI控制后电压上下振幅区间为580.0～622.5 V,采用滑模PI控制后电压上下振幅为573.8～620.6 V,且需0.06 s才能恢复稳定,即SAPF系统难以保证在该负载接入后直流侧电压的持续稳定;而SMES-SAPF系统受脉冲负载影响较小,在负载脉动时,直流侧电压仍可保持稳定且无振荡。

在1.20 s时直流侧参考电压突然增大到620 V,1.35 s时突然减小到600 V,仿真结果见图9(d),SAPF系统直流侧电压也会随参考电压的变化而变化,但在参考电压突增时,经PI控制下电压约0.04 s后趋于稳定,稳定后的电压距参考值约有0.6 V的误差,在参考电压突减时,稳定后的电压距参考值约有1.5 V的误差;采用滑模PI控制后,直流侧电压约0.02 s后趋于稳定,且误差较小;而采用滑模控制的SMES-SAPF系统不管是参考电压突增还是突减,均可保证在0.01 s之内直流侧电压准确无误地跟踪参考值。

不同控制策略下直流侧电压性能如表3所示。由表3可知,不同负载的接入几乎不会影响SMES-SAPF直流侧电压的稳定,且能始终保持较小电压幅值区间,均得益于超导磁储能装置特有的抑制振荡的特性,可见该储能装置的应用在提高电能质量和改善电力系统稳定性方面具有很大潜力。

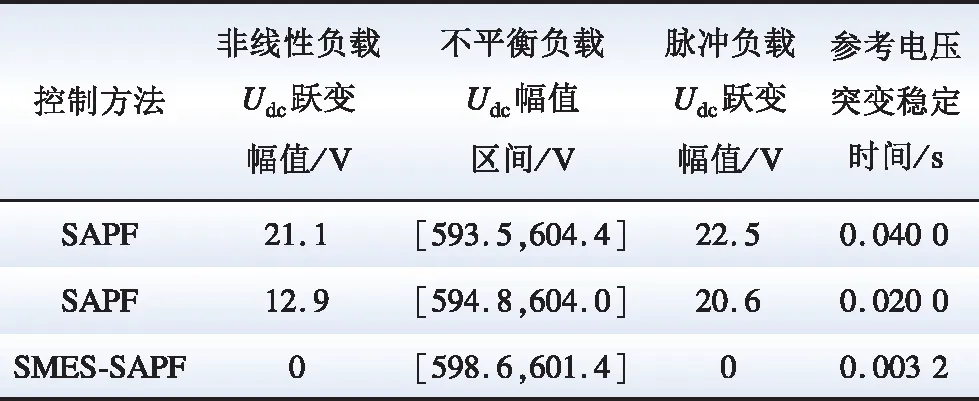
表3 不同控制策略下直流侧电压Udc性能分析Table 3 DC side voltage Udc performance analysis under different control strategies

5 结 论

本文在有源电力滤波器的直流侧增加储能设备构成新型拓扑结构——超导磁储能型有源电力滤波器,并针对不同负载接入时,常规控制策略补偿精度低的问题,提出了无源动态演化控制策略;同时为稳定直流电压,对直流侧斩波器采用滑模控制,通过实验得到如下结论:相比常规有源电力滤波器,超导磁储能型有源电力滤波器能更有效地解决不同负载接入时所引起的电能质量问题,且采用无源动态演化控制策略,能显著提高SMES-SAPF的补偿精度及其抗干扰能力;同时直流侧斩波器采用滑模控制可以实现直流侧电压准确无差地跟踪给定值并保持稳定,且能消除负载变化时直流侧电压波动对系统的影响。