考虑碳-绿证交易机制的虚拟电厂分布鲁棒优化调度
骆钊,耿家璐,黎博文,赵伟杰,罗蒙顺,马瑞
(1. 昆明理工大学电力工程学院,昆明市 650500;2. 中国南方电网有限责任公司超高压输电公司昆明局,昆明市 650500;3. 国网宁夏电力有限公司电力科学研究院,银川市 750011)
0 引 言
为加快完善生态文明建设整体布局,助力实现“双碳”战略目标,国家大力推动电力清洁能源的低碳发展。预计到2030年,我国风电、光伏装机容量将达到12×108kW以上[1]。虚拟电厂(virtual power plant,VPP)是发挥多能互补、低碳减排和清洁高效运行优势的关键抓手,对于现代能源体系低碳转型具有重要意义[2-3]。
目前国内外学者在虚拟电厂经济运行问题上已经进行了大量研究。文献[4]通过建立VPP的联合调度运行中心,使得分布式电源可以等效为1个联合发电实体参与电力市场调度,以提高VPP的经济性。文献[5]在建立VPP经济收益的目标函数以及风力发电厂和电池储能系统的收益、成本等数学模型的基础上,建立了可提供调峰和调频服务的VPP经济优化调度模型。文献[6]构建了以虚拟电厂效益最大为目标函数的基于分时电价的含风-光-气-储虚拟电厂经济调度模型。文献[7]建立了虚拟电厂热电负荷优化调度模型,对比了不同的虚拟电厂运行策略,并采用自适应免疫遗传算法进行求解,实现了虚拟电厂内部热电负荷优化调度。文献[8]计及虚拟电厂的售电收益、与主网交互收益、需求响应成本、削负荷成本以及机组运行成本,建立以虚拟电厂的预期日前收益最高为目标的优化调度模型。上述文献仅针对系统调度运行展开优化,未充分考虑碳排放带来的环境成本。
碳交易机制(carbon emissions trading,CET)和绿证交易机制(green certificate trading,GCT)为降低碳排放,提高可再生能源消纳率以及促进VPP经济发展提供了新的思路。文献[9]综合考虑运行成本、能源成本以及碳交易成本,建立适用于VPP的低碳经济调度模型。文献[10]引入碳排放交易机制,以虚拟电厂经济成本和碳交易成本最小为优化目标,构建虚拟电厂新型低碳经济调度模型,实现经济与低碳的协同优化。文献[11]搭建了一种考虑阶梯式碳交易与供需灵活双响应的VPP优化调度模型,在已有研究的基础上完善了实际的碳排放模型,考虑了气负荷的碳排放。文献[12]提出了一种考虑需求侧管理和碳交易的电-气互联网络分散式低碳经济调度模型,有效降低了系统的碳排放量。文献[13]设计了调频辅助服务绿色证书量化分配的方法,讨论补偿方法实施带来的效果和可能存在的问题。文献[14]构建了一种计及绿色电力证书交易制度的含风电电力系统经济调度模型。文献[15]构建了省级日前电力市场出清模型与国家绿证交易市场出清模型,讨论了可再生能源消纳配额百分数的变化对绿证价格的影响情况。上述文献侧重于对碳交易或者绿证交易的独立研究,未充分考虑绿证-碳交易联合减排策略。
VPP在运行过程中面临负荷及可再生能源出力等不确定性问题,鲁棒优化方法作为解决不确定性问题的重要手段,国内外学者已经进行了大量相关研究。文献[16]提出了计及充电负荷不确定性的充电站储能鲁棒优化配置方法,实现多约束条件下的储能系统综合成本最小化。文献[17]针对大规模风电并网给输电网投资规划带来严峻挑战提出数据驱动下两阶段分布鲁棒规划优化模型。文献[18]考虑风电时间相关性的多面体不确定性,提出了一种鲁棒机组组合模型。文献[19]针对风、光出力及负荷需求的不确定性造成虚拟电厂收益低的问题,建立了基于多场景技术的冷热电虚拟电厂优化调度模型,降低了风光出力及多能负荷不确定性的影响。文献[20]针对虚拟电厂面临的风电不确定性,构建了热电联产的两阶段鲁棒优化模型。上述鲁棒优化方法存在保守性强和求解效率低等问题。
与上述鲁棒优化方法相比,分布鲁棒优化方法(distributionally robust optimization,DRO)更能有效平衡系统的保守性和经济性。文献[21]提出基于KL散度的储能电站分布鲁棒规划方法,有效降低了运行成本、提高了风电消纳水平。文献[22]建立了确定分布式光伏电站接入配电网并网点和容量的分布鲁棒优化配置模型,在模型经济性和鲁棒性之间达到了良好的平衡。
考虑到系统运行不确定性,需要对系统运行过程中所面临的风险进行评估。文献[23]建立了一种基于投资组合理论中计及风险量度的虚拟电厂容量优化配置模型,为不同风险偏好的投资商在规划建设虚拟电厂时面对多电源容量配置问题提供定量依据。文献[24]建立了计及虚拟电厂的电力系统优化调度模型,利用条件风险价值(condition value at risk,CVaR)对系统运行成本进行风险管理,有效降低了系统风险。
综上所述,本文提出了一种考虑碳-绿证交易机制的虚拟电厂分布鲁棒低碳经济调度模型。首先,通过引入绿证-碳交易机制,并利用CvaR评估系统运行所面临的风险,以碳交易成本、绿证成本与能源成本之和最小为目标函数,建立考虑绿证-碳交易机制的区域虚拟电厂优化模型;其次,综合考虑1-范数和∞-范数构造概率分布模糊集,以调度系统可用的历史数据为基础,构建计及两阶段分布鲁棒的虚拟电厂优化调度模型;最后,研究碳-绿证交易机制、DRO以及CVaR对VPP运行成本的影响,为VPP低碳减排及稳定运行提供参考。
1 VPP碳-绿证交易模型
1.1 碳配额分配机制
本文采用计及补贴机制的阶梯型碳交易模型,超出碳配额的部分通过碳交易平台购买补足,配额有结余的可在后续年度使用,也可以用于配额交易。
根据《上海市2020年碳排放配额分配方案》[25],按照外部电网购电、内部能源发电和供热等不同结构,采用行业基准线法分配碳配额,具体核算方法如下:
(1)
式中:Ftotal为整个VPP的碳排放量;Fgt、Fgrid分别为燃气机组、从外部电网购电折算的碳排放量;γgt,p为综合修正系数;λgt,p为燃气机组的单位综合供电量碳排放基准;β为燃气轮机供热的热电折算系数;ρgrid为电网公司单位供电量线损率基准;λgrid,p为电网供电的单位发电量碳排放基准;Pgt,h、Pgt,p、Pgrid,p分别为燃气机组的供热量、燃气机组供电量以及外网购电量。
1.2 VPP碳交易成本计算模型
1) 实际碳排放核算方法。
本文依据《上海市温室气体排放核算与报告指南》[26],通过选取排放因子法计算VPP碳排放量,计算方法如下:
Fs=Fdirect+Findirect
(2)
式中:Fs为实际核算碳排放量;Fdirect为直接排放量;Findirect为间接排放量,计算公式如下:
(3)
式中:Kgas为燃料消耗量,本文中为天然气消耗量;Hlow为天然气低位热值;CH为天然气的单位热值含碳量;ξO为氧化率;μCO2为电力排放因子。
2) 阶梯式碳交易模型。
本文选用阶梯式碳交易机制,具体计算模型如下:
(4)
式中:CCO2代表碳交易成本;m代表交易市场的单位碳价;δ代表不同梯度的价格上升幅度;L代表碳排放等价区间长度。
1.3 配额制下的绿证交易机制
本文引入基于配额制的绿证交易机制,绿证数量和收益如式(5)和式(6)表示:
(5)
Cgre=cgreGgre
(6)
式中:Ggre表示系统内参与交易的绿证数量,本;Cgre为绿证收益,元;Pi为第i个可再生能源设备实际出力值,kW;Δt为调度时段时长,h;n为系统中可再生能源发电商数量;cgre为绿证价格。
2 VPP低碳优化模型
本文所提的虚拟电厂结构如图1所示。VPP聚合了风电机组、光伏机组、微型燃气轮机、余热回收锅炉、电锅炉、蓄热槽、热交换机、储能装置等。VPP控制中心与绿证交易平台、碳排放权交易平台、电力交易中心等进行信息通信,实现与大电网及天然气管网等能源系统的能量交互,当VPP能源过剩或者不足时可以通过各能源交易中心实现各能源系统与VPP的交易,满足用户用能需求。

图1 虚拟电厂结构Fig.1 Virtual power plant structure
2.1 目标函数
对于并网运行的虚拟电厂,引入文献[27]中的CVaR理论,其低碳经济调度模型目标函数如式(7)所示:
minC=γCEXP+(1-γ)CCVaR
(7)
minCEXP=Ce+Cgas+CES+CHS+CCO2-Cgre
(8)
(9)
式中:C为系统运行成本,元;CEXP为系统期望运行成本,元;CCVaR为系统CVaR,元;Ce为购电费用,元;Cgas为购买天然气费用,元;CES为储电设备运行维护费用,元;CHS为储热设备运行维护费用,元;CCO2为碳交易成本,元;γ为风险偏好相关系数,表示期望成本在运行成本中所占的比重;1-γ为CVaR在运行成本中所占的比重;η为风险价值;σ为置信水平。
1) 购电费用公式为:
(10)
式中:cgrid,t为t时刻系统的购电价格;h为调度周期,24 h;Pgrid,t为t时刻VPP与电网之间交换功率。
2) 燃气费用公式为:
(11)
式中:cgas为天然气单位热值价格;PGT,t表示t时刻微型燃气轮机的发电功率;ηGT为微型燃气轮机效率。
假设蓄电设备单次充放电的使用成本相同,购买成本为Cbattery,无损坏情况下使用次数为Nu,则其每次完全充放电成本cr为:
(12)
3) 蓄电设备运维成本公式为:
(13)
式中:Ccapacity为蓄电设备的容量;PES,C/D,t为时段t时蓄电设备的充放电功率。
4) 储热设备运维成本公式为:
(14)
式中:cHS为单位储热运维成本;QHS,C/D,t为时段t时储热设备的充放热功率。
2.2 约束条件
1) 绿证交易价格约束:
(15)
(16)

2) 电气母线约束:
Pgrid,t+PGT,t+PPV,t+PWT,t+PES,D,t=
LE,t+PES,C,t+PEB,t
(17)
式中:Pgrid,t表示t时刻购电功率;PGT,t表示t时刻微型燃气轮机发电功率;PPV,t表示t时刻光伏的发电功率;PWT,t表示t时刻风机的发电出力;PES,C,t、PES,D,t分别表示蓄电池t时刻的充、放电功率;LE,t为电负荷;PEB,t表示t时刻电锅炉的运行功率。
3) 热交换器约束:
LH,t=ηHX·QHX,t
(18)
式中:ηHX表示热交换器的效率;QHX,t表示t时刻输入热交换器的功率;LH,t表示t时刻热负荷功率。
4) 电锅炉运行约束:
(19)
QEB,t=PEB,tηEB
(20)

5) 热母线约束:
QHX,t+QHS,C,t=ηWH·QWH,t+QEB,t+QHS,D,t
(21)
式中:ηWH表示余热锅炉的产热效率;QWH,t表示t时刻余热锅炉的产热功率。
6) 燃气轮机热电平衡约束:
(22)
式中:αGT表示燃气轮机的热电比。
7) 燃气轮机运行约束:
(23)

8) 蓄电设备运行约束:
(24)

9) 购电功率约束:
(25)

10) 储热设备运行约束:
(26)

3 考虑风光不确定性的分布鲁棒优化调度模型
3.1 两阶段分布鲁棒优化模型构建
为便于下文的两阶段VPP调度模型分析,将第2节构建的VPP模型相关的优化变量分类为第一阶段变量和第二阶段变量。
其中第一阶段决策变量用x表示,不包含不确定性参数,即与风、光电场景无关,同时第一阶段还制定了常规机组的启停机计划。第二阶段变量为灵活调节变量,在第一阶段变量已知的情况下,可根据风光实际出力进行相应调节,如各机组出力等,用y表示。为简化分析,将第2节构建的VPP优化调度模型表达为如下线性矩阵形式:
(27)
式中:a、b代表对应成本系数;ξ代表不确定参数值;G、E、H、I、J、O分别对应相关约束中变量的系数矩阵;d、h、o为常数列向量,等式约束主要为各母线功率平衡方程以及储能设备的储能关系式,不等式约束为各设备的运行约束。
两阶段分布鲁棒优化模型需针对最恶劣情况下不确定量在不确定集内的变化寻求最优调度解,其标准形式为:
(28)
式中:D是场景概率分布的集合,即综合范数模糊集;N为离散场景个数;Pn为场景n的分布概率;x为第一阶段机组启停标志变量及机组运行状态变量;y=[y1,y2,…,yN]表示第二阶段连续决策变量;ξ=[ξ1,ξ2,…,ξN]为第二阶段离散决策变量;c、b、f、z为相应的向量。
其中,概率分布的置信度为[28-29]:
Pr(‖p-p0‖1≤θ1)≥1-2N·exp(-2Kθ1/N)
(29)
Pr(‖p-p0‖∞≤θ∞)≥1-2N·exp(-2Kθ∞)
(30)
式中:K为样本数量;θ1和θ∞为概率偏差允许值;p为概率分布实际值;p0为概率分布预测值。
用α1和α∞来表示置信度,则式(29)、(30)可变化为:
(31)
(32)
由上式综合可得概率分布的置信集合:
(33)
3.2 两阶段分布鲁棒优化模型及求解方法
本文采用列约束生成算法(column-and-constraint generation,CCG)对两阶段鲁棒优化调度模型进行求解,将问题分为主问题与子问题,相比于Bender分解法,CCG算法具有适用性强、复杂程度低、求解效率高以及收敛特性好的优点。首先,由子问题求解最恶劣概率分布,实时调节机组出力;再由主问题模型满足预测场景及子问题生成的最坏场景相关约束,得到最优解[30-31]。二者分别提供下界值和上界值。
1) 主问题:
(34)
2) 子问题:
(35)
由子问题式(35)可得,当已知主问题求解的结果时,寻找置信区间内的最恶劣场景概率分布,得模型下界值。由于外层与内层问题的约束范围不相关,故可将式(35)分解为2步进行求解,即先求解内层优化问题,再对外层max求解,如式(36)和式(37)所示:
(36)
(37)
其中,l由主问题的求解结果得到,由于模糊集中的绝对值约束为非线性约束,所以需要对其进行线性等效分解,对绝对值约束进行等效转化得到:
(38)

4 算例分析
4.1 基础数据
为验证所提优化模型的有效性,选择云南某VPP作为仿真对象,包含风电、光伏设备,电锅炉,储电/储热设备和3台微型燃气轮机等,采用Gurobi+Cplex对模型进行仿真求解。
根据2020年上海碳市场现货交易走势及成交数据[32],取基准碳配额价格为40元/t,绿证单价取60元/本。天然气价格为3.45元/m3,折算为单位热值价格为0.349元/(kW·h)。储电设备购买成本为67.2万元,无损情况下充放电次数为6 000次。各个设备的最大容量和运行参数如附录A表A1所示。碳交易相关参数设置见附录A表A2。负荷及可再生能源出力数据如附录A图A1所示。设置5个不同情景:
情景1:不加入DRO,不加入碳交易和绿证交易机制。
情景2:加入DRO,不加入碳交易和绿证交易机制。
情景3:加入DRO,仅加入碳交易机制。
情景4:加入DRO,加入碳交易和绿证交易机制。
情景5:加入DRO,考虑CVaR,加入碳交易和绿证交易机制。
4.2 优化结果分析
4.2.1 不同优化模型对比
为了比较不同优化模型,在情景4中选择以1/4预测值生成10 000个随机模拟场景进行优化。其中,选用α∞为0.8时的情况进行对比。
从表1可以看出,在最恶劣情景下,分布鲁棒相比鲁棒优化方法(robust optimization,RO)和随机优化方法(stochastic optimization,SO)更能兼顾系统经济性和保守性。
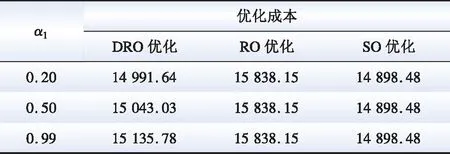
表1 不同案例下运行总费用Table 1 Total operating costs in different scenarios 元
4.2.2 不同场景对比分析
为验证引入绿证-碳交易机制的优势,并考虑不确定参数波动给总成本带来的影响,设定分布鲁棒优化模糊集置信度水平α1、α∞分别为0.20和0.99,离散场景N设为10,取不参与碳交易的情景2中的碳排放总量作为碳排放成本所需计及的碳排放总量,经仿真计算为46.13 t/天。参与碳交易的场景中每梯度碳价涨幅系数[2-13]δ取0.25,5种运行方式下虚拟电厂的运行成本如表2所示。

表2 不同案例下的优化结果Table 2 Optimization results in different scenarios
从表2可知,在不考虑CET与GCT机制的情况下,考虑系统鲁棒性的情景2相较于情景1成本有所增加,碳排放量有所降低;相较于仅考虑碳交易的情景3,计及碳-绿证联合交易的情景4成本降低了5.1%,碳排放量减少了8.48%;考虑DRO优化策略的情景4相较于情景2的运行成本降低了7.83%,碳排放量减少了11.45%,其经济性和低碳性得到明显改善,这是因为引入GCT和CET机制提高了可再生能源的消纳,激励系统降低碳排放。情景5加入CVaR之后系统运行成本比情景4提高了8.78%,碳排放量增加了2.71%,这是因为VPP运行需要面临更大的风险,系统决策更加保守所致。
4.3 机组优化结果分析
VPP机组优化调度结果如图2、3所示。其中,图2为VPP机组电负荷优化调度结果,当机组向微电网输出功率时取值为正,反之则取值为负;图3为VPP机组热负荷优化调度结果。采用的阶梯电价示意图如附录A图A2所示[33]。

图2 电负荷优化出力情况Fig.2 Optimization of force situation by electric load
如图2所示,在VPP优化调度过程中,风电在1—24时全程出力,而在1—7时和24时,VPP的负荷主要依靠微型燃气轮机、储能、风光及电网供给。此时,当电网日前交易电价低于微型燃气轮机单位发电成本时,微型燃气轮机输出功率最小;在8—23时,因日前交易电价较高,微型燃气轮机输出功率增大,VPP减少对电网的购电量,进而降低运行成本。同时,蓄电池在1、3、13、15—18以及24时进行充电,在8—11和12、20、23时进行放电,实现削峰填谷。
如图3所示,在1—7时以及24时,因为该时段电价较低,VPP热负荷由电锅炉独立供给;在8—23时,电价较高,微型燃气轮机输出功率增大,热负荷主要由其供应。
4.4 不同碳交易价格对运行成本的影响
从图4可以看出,当碳交易基价小于210元/t时,系统运行成本随碳交易基价增大而增大,当基价大于210元/t时,系统的碳排放量曲线下降速度变缓,这是由于较高的碳交易价格激励系统调整机组出力限制碳排放量,碳交易价格越高,系统对碳排放量的约束越强,碳收益越大,运行成本也相应降低。
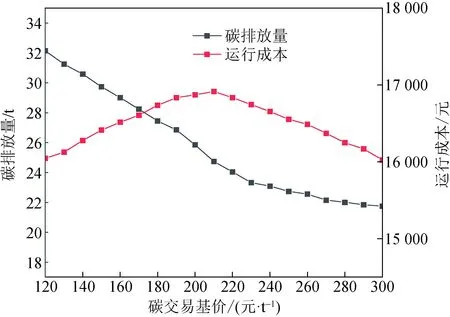
图4 碳交易价格对VPP影响Fig.4 Impact of carbon trading price on VPP
4.5 不同置信区间下的调度结果对比分析
为验证考虑风光不确定性的DRO优化调度模型的有效性。选取数据样本为200,设置考虑综合α1和α∞,只考虑α1以及只考虑α∞的情况下进行仿真,其中,只考虑α1时,选取α1=0.50,0.20≤α∞≤0.99;只考虑α∞时,选取α∞=0.99,0.20≤α1≤0.99。系统运行结果如表3—5所示。

表3 不同置信区间下运行费用Table 3 Operating costs under different confidence intervals 元
从表3得出,随着α1和α∞的增大,概率分布允许偏差也增大,使得系统不确定性增大,进而导致运行成本增加。当α∞的值较小且保持不变而α1值增大时,系统成本并没有随之增大,说明此时系统优化成本主要受∞-范数影响。
从表4、表5可以看出,对比考虑1-范数或者∞-范数约束,综合范数模糊集约束情况下系统优化运行成本最低,更能兼顾系统运行保守性和经济性。
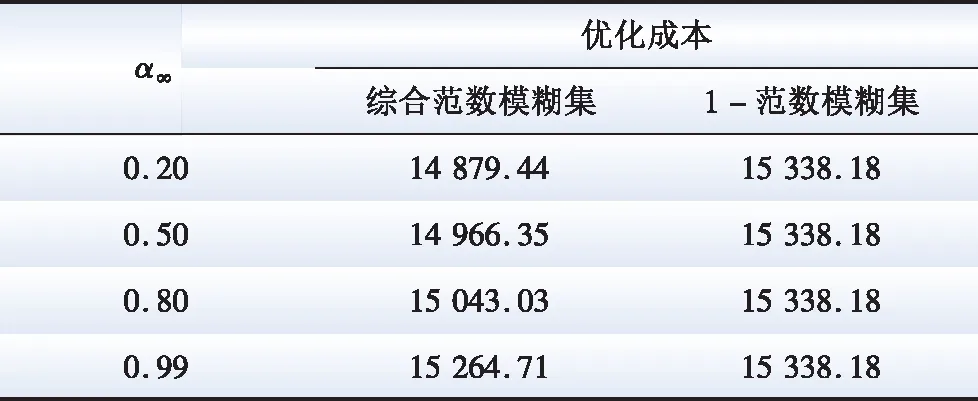
表4 α∞变化时成本对比Table 4 α∞ change cost comparison 元

表5 α1变化时成本对比Table 5 α1 change cost comparison 元
4.6 不同置信区间下的调度结果对比分析
图5为不同CVaR置信水平对系统运行成本的影响。从图5可以看出置信水平越大,系统运行成本越大,说明系统运行需要应对越大的不确定性风险,这时系统运行调度人员需要考虑系统运行经济性和保守性。

图5 CVaR置信水平对系统运行成本影响Fig.5 Impact of CVaR confidence level on system operation cost
图6为不同风险偏好系数对系统运行成本的影响。从图6可以看出,CVaR比重和期望成本比重之和为1,随着风险偏好相关系数不断增大,系统期望成本比重逐渐升高,系统运行成本逐渐降低,这是因为系统需要应对的运行风险较大;相反,当风险偏好相关系数不断减小,CVaR比重变大,运行成本会随之增大,这是因为系统需要应对的运行风险较小。因此,调度人员需结合系统对经济性与保守性的重视程度来权衡运行成本与运行风险,确定最终的调度方案。

图6 不同风险偏好相关系数对系统运行成本的影响Fig.6 The impact of different risk preferences on the operation costs of the system
4.7 算法分析
选取α1、α∞分别为0.2和0.99,M为200,对CCG算法进行分析。从图7可以看出,经过2次迭代,主问题与子问题之差小于给定精度,迭代求解停止,表明CCG算法能快速求解本文所提出的DRO模型。

图7 CCG算法迭代结果Fig.7 CCG algorithm iteration results
5 结 论
本文提出了考虑绿证-碳交易机制影响下的虚拟电厂分布鲁棒低碳调度模型。分析了不同机制对系统运行成本的影响,得出以下结论:
1) 绿证-碳交易机制的引入降低了系统运行成本,能够进一步促进企业绿色转型意愿。
2) 相比于传统两阶段鲁棒和随机优化的方法,本文所提的分布鲁棒能更好兼顾系统经济性和保守性。
3) 本文考虑综合范数模糊集,相对于只考虑单个约束条件的情况,其优化效果更明显,保守性更低。同时,所选算法能对鲁棒模型快速求解。
4) CVaR能充分衡量调度中的风险状况,结合系统对经济性与可靠性的重视程度来权衡运行成本与运行风险,确定最终的调度方案,规避运行过程中所面临的风险。
附录A
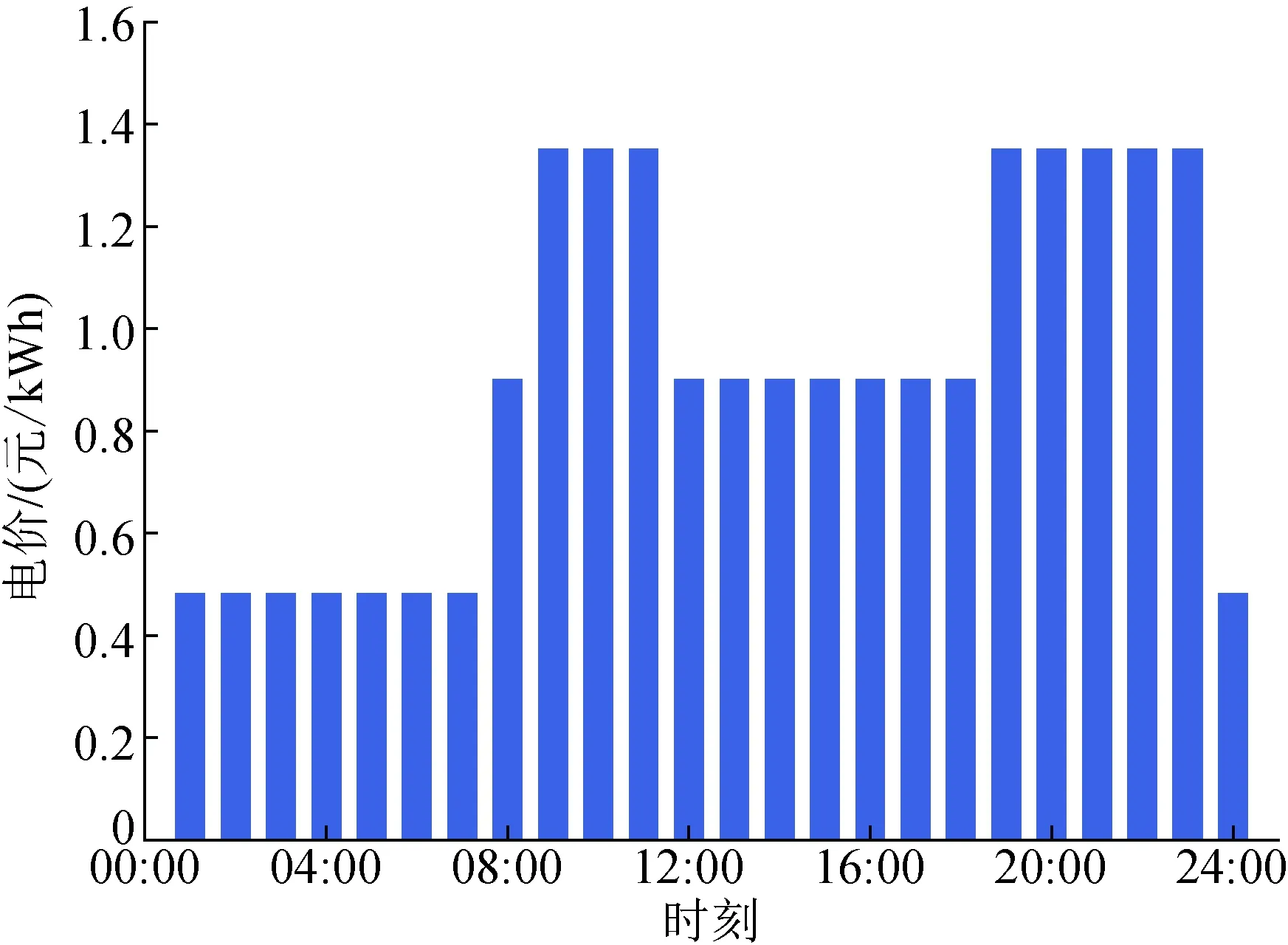
图A2 分时电价Fig.A2 Time sharing electricity price
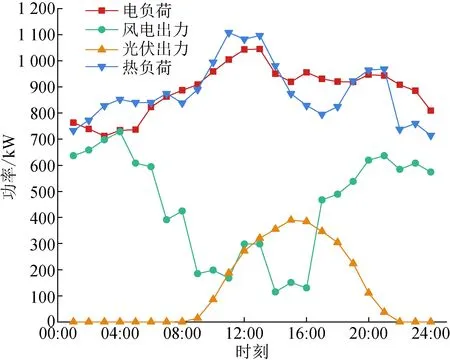
图A1 可再生能源发电及负荷数据Fig.A1 renewable energy generation and load data

表A1 系统中各设备容量及参数Table A1 Equipment capacity and parameters in the park

