基于确定-随机子空间的电力系统外部系统暂态等值
赵妍,柳旭,孙硕,朱建华,聂永辉
(1.东北电力大学输变电技术学院,吉林省吉林市 132012;2.国网平湖供电公司,浙江省平湖市 314200;3.国网四平供电公司,吉林省四平市 136000;4.润电能源科学技术有限公司,郑州市 450000;5.东北电力大学教务处,吉林省吉林市 132012)
0 引 言
以新能源为主体的新型电力系统呈现高度电力电子化特征。新型电力系统具有发电单元多、单体容量小、交直流相互耦合等特点,这些特点使得传统电网仿真分析技术的局限性日益凸显。高比例新能源接入情况下,电力系统运行机理更加复杂,故障不确定性更强,传统安全防御体系不具备灵活应对不确定性故障的能力,无法保障复杂故障条件下的电网安全运行,连锁脱网事故多次发生。暂态仿真通过故障还原,提高应对不确定性故障的能力,一定程度上保障了复杂故障条件下的电网安全运行,支撑了构建清洁、低碳、安全、高效的能源体系。
但是,目前尚缺乏认识其机理的有效模型和仿真工具[1-6]。主要原因有:对新能源发电机技术研发持续投入、机组型号众多,且不断进行技术更新,通用化建模难度巨大。由于商业保密等原因,厂家提供的多为黑箱模型。风力发电机组的控制新技术快速发展、控制系统控制参数多、测试难度大、模型整定困难。模型的不准确使得电网运行方式更加保守,严重制约了新能源的消纳。
实际上,若对大电力系统进行全面的电磁暂态仿真,往往耗时很长。而对电力系统进行暂态分析时,一般也只是关注其中的某一部分相关变量的暂态变化过程,因此,可以只对“感兴趣”的部分网络进行详细的仿真,而对于其余部分网络(文献[7]中称之为“外部系统”)进行建模等效简化,可以加快暂态仿真的进程[7]。
电力系统外部系统电磁暂态等值方法分为两类。一类方法是工频下的ward外部系统等值,这类方法是通过对电力网络进行星网变换而获得。对于伪稳态运行的系统具有较高的等值精度。但是当系统发生不对称故障或者设备饱和时,系统中谐波分量丰富,尤其是需要研究系谐波信号的影响时,这种等值方法的误差比较大;而且该方法要求接口必须选在电压或电流数值相对稳定的节点处,否则仿真计算时易出现振荡[8-12]。另一类是与频率相关的等值方法(frequency dependent network equivalents,FDNE)[13-19],这类方法是在一个宽频段范围内对外部系统进行等值,使得在选定的频率范围内,等值系统对研究系统的作用和影响近似或接近于外部系统对研究系统的作用和影响。文献[13-18]提出了采用基于阻抗(导纳)状态空间表达式的矢量拟合(vector fitting, VF)等值算法。这类方法通过对外部系统进行频率采样,利用最小二乘法,求解系数矩阵为稠密矩阵的超定线性方程组,来获得状态空间表达式的相应系数矩阵。其等值网络能够在较宽频段内对外部系统均具有较高的近似度,但计算量较大,且所求得的极点可能出现不稳定极点。文献[19]提出了研究风电并网系统振荡问题的频域模式分析方法,使用外部系统阻抗网络模型描述目标系统,通过求取网络节点导纳矩阵和回路阻抗矩阵的行列式零点,获得系统的振荡模式,并根据矩阵的左和右特征向量,计算出各节点和支路对振荡模式的参与因子、可观度和可控度指标。这种方法在一个较小频率范围内具有较好的等值效果;当频带较宽时,等值效果仍不够理想。
与频率相关的系统等值方法(例如文献[13-19])的核心问题是需要获得准确的状态空间表达式。确定-随机子空间(combined deterministic-stochastic identification,CDSI)在宽频段范围内是辨识状态空间表达式的方法。CDSI是随机子空间(stochastic subspace identification,SSI)算法的提升方法。SSI方法假定白噪声输入,仅利用输出信号,辨识状态空间表达式,在进行系统参数求解时无法建立确定的激励-系统-响应模型,存在主导模态提取困难,引入虚假模态[20-22]的问题。CDSI能利用输入(激励)和输出(响应)全部信息进行模态参数识别,建立确定的激励-系统-响应模型。防止系统特征值解空间的扩大,可以解决密集模态识别困难、虚假模态较多等问题,同时保留了SSI计算量小、极点稳定等优点,提高了状态空间表达式的辨识精度和等效模型的可靠性。
本文基于外部系统的输入和输出数据,利用CDSI对状态空间表达式的系数矩阵进行辨识,根据零极点构建RLCG等值电路,进行建模等效简化,实现了新型电力系统外部系统的等值构建。
1 方法原理
1.1 确定-随机子空间原理
1.1.1 CDSI原理
CDSI方法是将输入、输出数据组成特定的Hankel矩阵,计算Hankel矩阵的行空间投影,对投影进行奇异值分解,从而得到可观测矩阵和状态序列的卡尔曼滤波估计[23-25],进而确定系统矩阵A、B、C、D。确定-随机系统可以表示为图1。

图1 确定-随机系统Fig.1 Deterministic-stochastic identification
图1中A为状态矩阵,B为输入矩阵,C为输出矩阵,D为传递矩阵,u为输入数据,y为输出数据,x为状态向量,w称为过程噪声,v称为量测噪声。下标k表示序列长度。
假设系统量测到的输入U、输出Y的时间间隔为Ts,U、Y分别为长度为k的序列,ui、yi为l个通道在i时刻的观测向量。如果考虑上述随机因素的干扰,那么就得到确定-随机状态方程:
(1)
设噪声为白噪声序列,且协方差矩阵如下:
(2)
式中:E(·)代表数学期望因子;δpq代表kronecker函数;Q、S、R为噪声序列的协方差矩阵。这样,CDSI方法的基本目标是:已知输入数据u0,u1,…,uk和输出数据y0,y1,…,yk,确定系统合适的阶次n后,求得系统矩阵A、B、C、D、Q、R、S。下标p、q表示长度为k的序列中的任意项。
1.1.2 CDSI算法流程
CDSI算法的流程具体如下:
1)通过输入、输出数据构建Hankel矩阵[26]。
(3)
式中:U0|2i-1下标的第一个数字代表Hankel 矩阵左上角元素的时间系数,下标第二个数字代表Hankel矩阵左下角元素的时间系数,假设j→∞;将输入数据Hankel矩阵U0|2i-1分为两部分,上部分称为“过去”输入,用下标“p”表示,即Up;下部分称为“将来”输入,用下标“f”表示,即Uf。同理,输出的Hankel矩阵Y0|2i-1也用同样的方法定义。
定义输入和输出的Hankel矩阵的集合为W0|2i-1,则:
(4)
式中:Wp为“过去”集合;Wf为“将来”集合。
2)对Hankel矩阵进行QR分解:
(5)
式中:R11、R21、R22组成三角矩阵,Q1、Q2组成正交阵。
3)将输出Yf投影到输入和输出Wp空间,由空间投影的性质得出行空间的正交投影Pi:
(6)
4)对投影矩阵Pi进行奇异值分解(singular value decomposition,SVD)确定系统阶数:
Pi=USVT
(7)
式中:U和V为正交矩阵;S为降序排列的奇异值组成的对角矩阵。
理论上矩阵S主对角线中非0元素个数就是模型阶数n。当受到噪声污染时,非零奇异值的个数大于模型阶数n,但数值都很小。
利用奇异值的相对变化率,即模型阶次指标(model order indicator,MOI)作为奇异值突降指标判断模型阶数n。奇异值突降指标记作Moi,i。
σ1≥σ2≥…≥σn
(8)
(9)
式中:σi为降序排列的奇异值。
设初始系统阶数为N,由于奇异值是降序排列的,在突降点大的地方,模型阶次指标Moi,i也是一个大值,即Moi,i最大值对应的阶次为模型的阶次n。系统阶数N=n+1(n为模型阶数,1为噪声阶)。
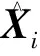
(10)
(11)
(12)
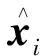
6)使用卡尔曼滤波状态序列和输入输出代入状态空间方程求得系统状态矩阵A、B、C、D和残差矩阵pw、pv。
(13)
求系统状态矩阵A的特征值λ(i=1, 2,…,n),进而可获得频率f′i。
1.2 等值模型
用yk表示电流I;uk表示电压U。状态空间表达式Y(s)为:
(14)
式中:A、B、C、D为已知的系数矩阵;E为单位矩阵;I(s)、U(s)、Y(s)为频域下输入、输出及对应关系,其中s是频域下的自变量。
将式(14)转化为频域表达式,其中m≥n:
(15)
式中:an、bm为降幂排列项系数,下同。
pi表示实数极点;p′k±p″k表示复数极点,可将式(15)写为:
(16)
裂项得:
(17)
在得到外部系统电流和电压的传递函数后,可用3×3简单网络代替外部系统,则该网络可作为外部系统的等值系统。并联等值模型如图2所示。

图2 并联等值模型Fig.2 Parallel equivalent model
在图2中,实数极点对应RL支路:
(18)
(19)
(20)
式中:YRL(s)为RL支路对应关系;R、L、C、G为等效支路元件参数,下同。
复数极点对应RLCG支路:
(21)
(22)
R=[-2p′k+2(c′kp′k+c″kp″k)L]L
(23)
(24)
G=-2(c′kp′k+c″kp″k)CL
(25)
2 基于CDSI的外部系统等值方法流程
本文的方法包括CDSI辨识态空间表达式和构建RLCG等值电路两部分。
2.1 CDSI部分
CDSI部分的流程具体如下:
1)初始化CDSI,构造确定-随机状态方程和噪声协方差矩阵。
2)利用划定为外部系统的电压、电流采样数据构建Hankle矩阵。
3)将卡尔曼滤波状态序列和输入输出代入状态空间方程,求得系统状态矩阵A、B、C、D。
2.2 RLCG等值部分
RLCG部分的流程具体如下:
1)将状态空间表达式转化为频域形式,求解系统零极点。
2)将实数极点和复数极点分别对应其等效支路,构建外部系统等效电路图。
2.3 本文等值方法流程图
本文CDSI等值方法流程图如图3所示。
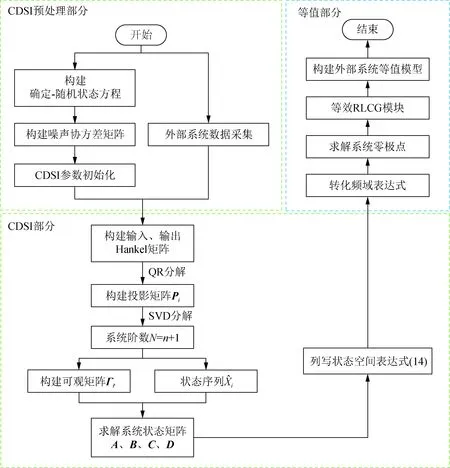
图3 CDSI等值方法流程图Fig.3 CDSI equivalent method flowchart
3 仿真验证和对比分析
3.1 仿真验证
以IEEE 14节点系统电网结构为例进行仿真分析,该拓扑图包含:14条母线,2台发电机,3台同步电动机,11个负荷点,20条输电线路和40个断路器[28]。在IEEE 14标准测试电力系统中节点14处,接入永磁直驱风电机组,组成分布式风电场,参数如表1所示[29]。仿真中,在风电场内部设置故障,将风电场视为内部系统,IEEE 14标准测试电力系统视为外部系统。具体接线如图4所示。
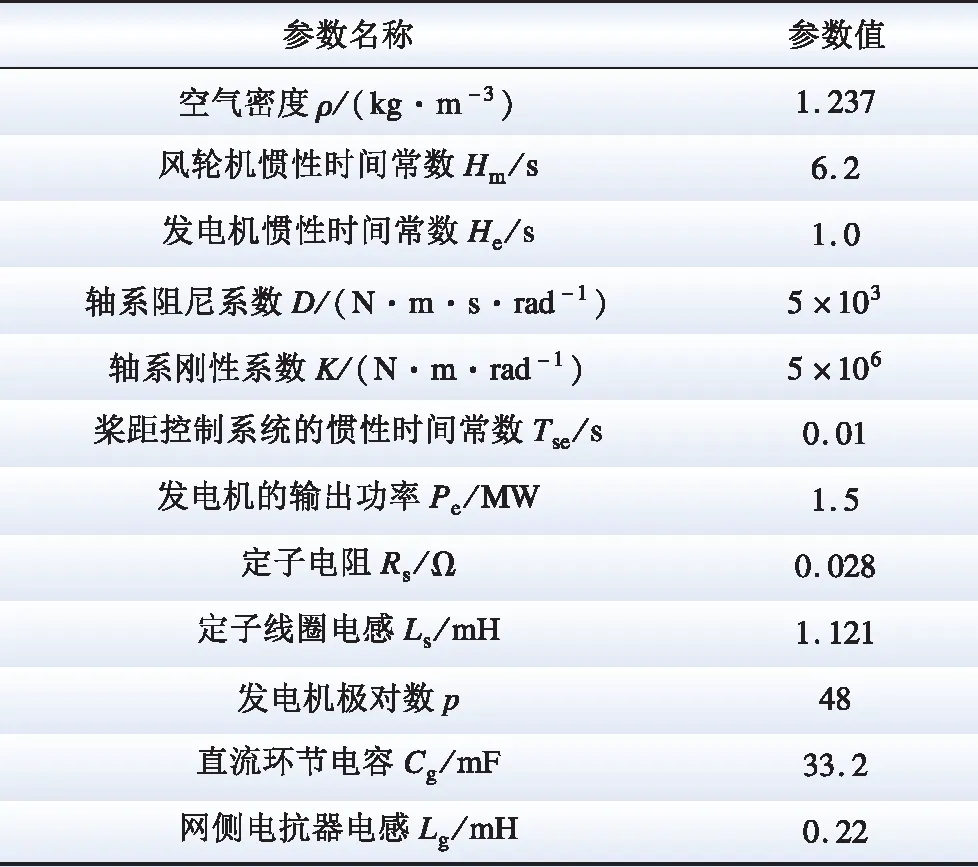
表1 永磁直驱风电机组参数Table 1 PMSG parameters

图4 接入风电机组的IEEE 14节点系统Fig.4 IEEE 14-node bus system connected to wind power
当风电场稳定运行后,在所连母线15设置持续0.05 s的三相瞬时性短路接地故障,引起分布式风电场功率振荡。
取节点14切除故障后、恢复稳定运行前三相电压、电流暂态数据。
构建CDSI状态方程,通过确定-随机子空间辨识,SVD分解得模型阶次指标Moi,i,如图5所示。

图5 模型阶次指标MOI曲线Fig.5 The curve of the model order indicator
由图5确定,模型阶数n为6,系统阶数N为7。使用卡尔曼滤波状态序列和输入输出代入状态空间方程式(13)求得系统状态矩阵A、B、C、D,其中系统矩阵A为:
(26)
根据CDSI辨识结果按照式(14)构建状态空间表达式,并转化为频域形式式(15),求解零级点并裂项式(16)—(17),将1组实数极点项和3组复数极点项按照式(18)—(25)构建RLCG等值电路,结果如图6所示,实现了外部系统暂态等值构建。

图6 电力系统外部系统暂态等值结构Fig.6 Transient equivalent structure of the external system of the power system
其中以A-A相为例,其等效电路图如图7所示,相关参数见表2。
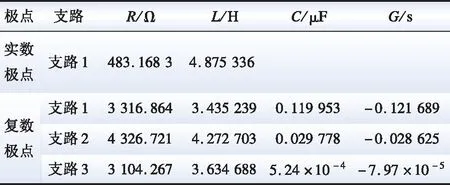
表2 CDSI算法A-A相RLCG等值电路参数Table 2 A-A phase RLCG equivalent circuit parameters of CDSI

图7 CDSI算法A-A相RLCG等值电路Fig.7 A-A phase RLCG equivalent circuit of CDSI
3.2 对比分析
1)采用SSI方法[18],假定输入为白噪声,输出为上例中采集的电压暂态数据,构建Hankle矩阵并进行奇异值分解,求得系统矩阵A和C之后,获得传递函数式(12)。
2)采用VF方法[12-16],将上例中采集的电压、电流暂态数据组成一个超定线性方程组:
(27)
式中:h和d表示一次项参数和常数。
通过求解线性方程组的最小二乘解可以获得新的极点,经过6次迭代后结果收敛,获得误差范围内的近似解ai、ci、d和h,获得传递函数式(13)。
将SSI、VF算法所得到的传递函数,分别采用本文RLCG等值方法,对外部系统进行等值计算而获得了相应的3输入3输出的等值网络。其中SSI的A-A相等值电路及相关参数如图8和表3所示,VF方法的如图9和表4所示。
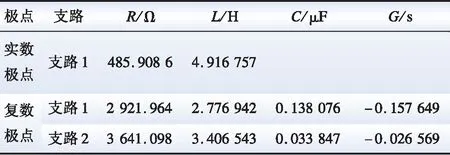
表3 SSI算法A-A相RLCG等值电路参数Table 3 A-A phase RLCG equivalent circuit parameters of SSI
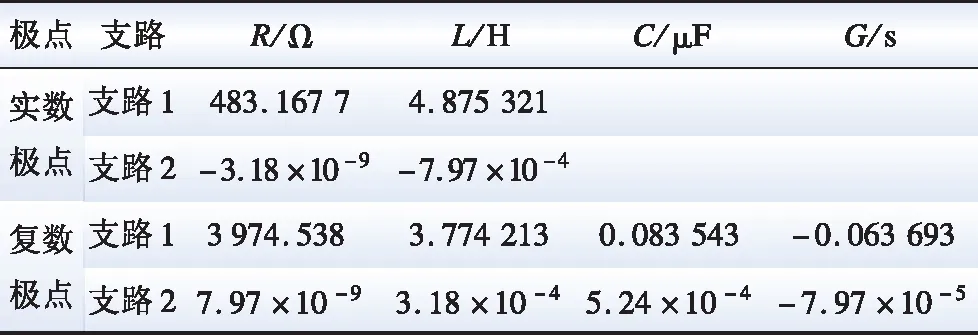
表4 VF算法A-A相RLCG等值电路参数Table 4 A-A phase RLCG equivalent circuit parameters of VF

图8 SSI算法A-A相RLCG等值电路Fig.8 A-A phase RLCG equivalent circuit of SSI
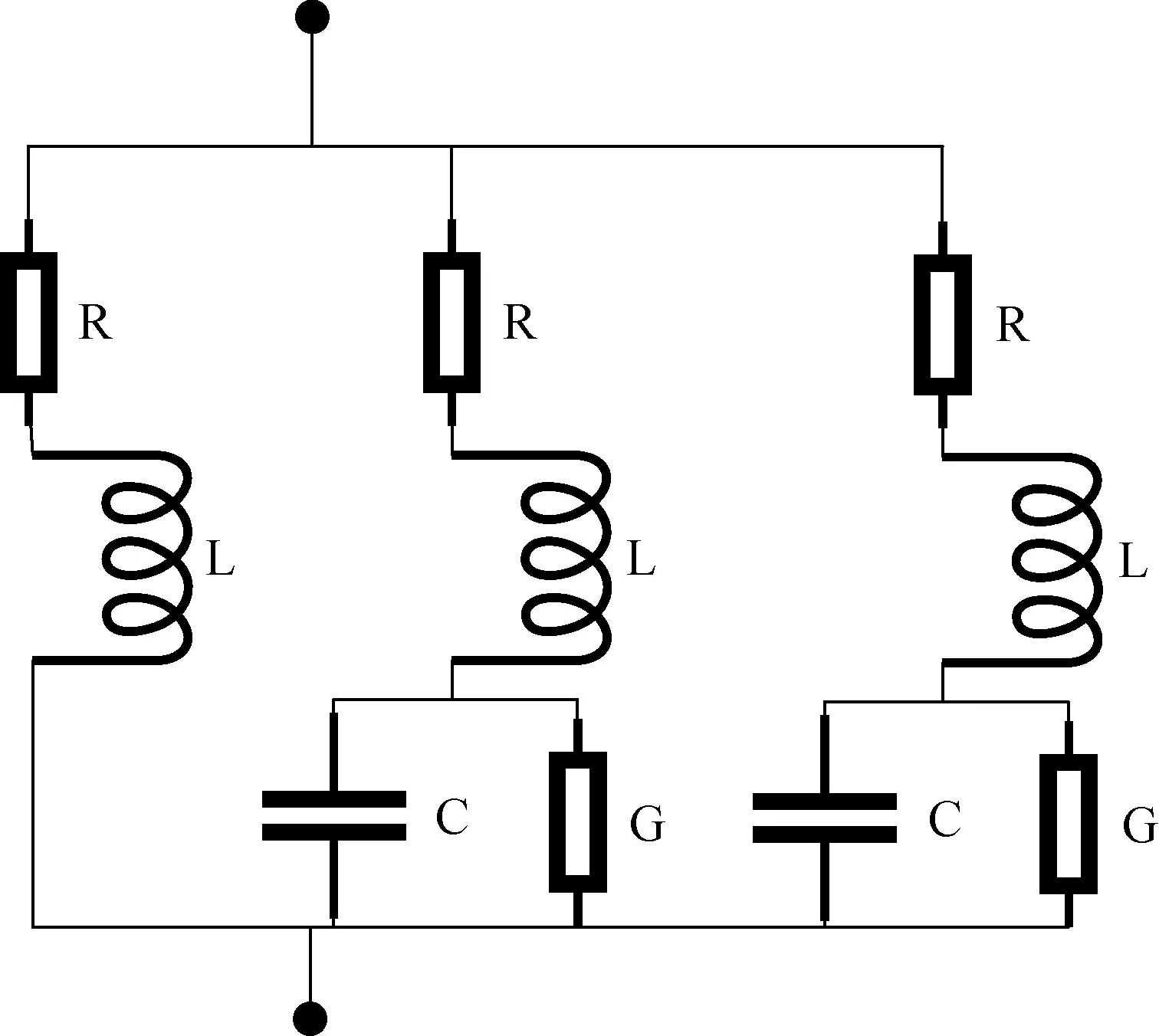
图9 VF算法A-A相RLCG等值电路Fig.9 A-A phase RLCG equivalent circuit of VF
用等效后的外部系统(见图6)替换原标准IEEE 14节点系统电网,分别对比CDSI与SSI、VF算法等效前后风力发电机故障后0.1 s电磁转矩,结果见图10。
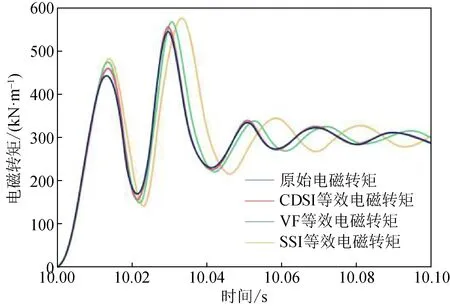
图10 电磁转矩对比图Fig.10 Electromagnetic torque comparison
分别计算电磁转矩的均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均相对误差(mean relative error,MRE)以及拟合优度(R2),其结果见图10和表5。
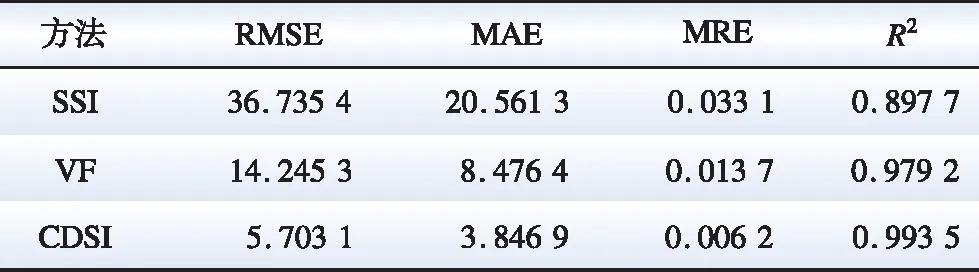
表5 电磁转矩误差Table 5 Electromagnetic torque error
结合图10和表5可以得到,CDSI等值方所得到的风电机电磁转矩曲线与未等值时的电磁转矩曲线几乎完全重合,误差参数最优,拟合度最高,可以获得准确的外部系统的暂态等值建模,优于VF和SSI方法。
VF方法计算量大,在求解暂态信号中出现了不稳定节点。而SSI方法仅利用输出信号,对主导模态提取时出现了虚假模态,使得最终结果误差较大。
4 实例分析
2015年某月,我国某风电场发生脱网事故,导致300 km外火电机组的转轴扭振保护(torsional tress relay,TSR)动作[30],引起火电机组停运。
根据录波数据和事故报告,由于风电场内部发生次同步振荡并在多级电网中传播引起电网功率振荡,火电机组扭振保护装置动作,造成机组跳闸,最终使电网频率由50.05 Hz降低至49.91 Hz。为简化系统,方便分析风电场内部的次同步振荡形成机理,将故障风电场划分为内部系统。对其余的外部系统进行等值简化,其电网结构如图11所示。

图11 电网拓扑结构图Fig.11 Grid topology diagram
已获得了故障后该地区风电场110 kV母线三相电压、电流60 s内的录波结果。限于篇幅,文中仅给出A相的电压和电流的录波结果,如图12、13所示,采样频率为12.8 kHz。取波动明显的25~31 s数据进行分析。

图12 电压录波结果Fig.12 Voltage recording results

图13 电流录波结果Fig.13 Current recording results
取25~31 s的电压和电流数据,利用本文的CDSI辨识等值方法,对量测数据进行参数辨识,获得状态空间表达式及传递函数,按零极点构建外部系统的RLCG等值电路,得到外部系统等值模型。
重构电流输出信号,其电流输出结果和局部放大如图14、15所示,分别对比CDSI、SSI、VF算法输出结果如图16所示,输出电流的误差结果如表6所示。
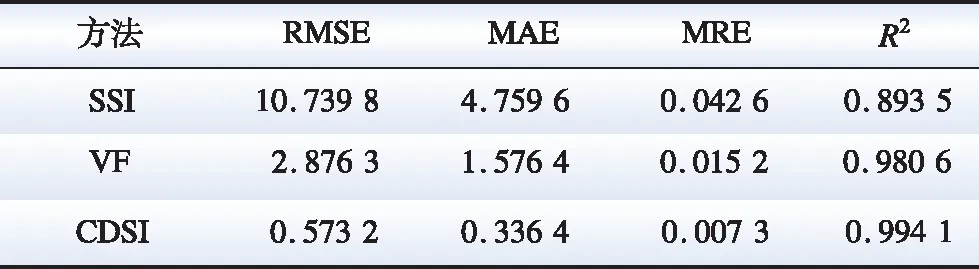
表6 电流输出的误差值Table 6 The error value of the current output

图14 电流输出结果Fig.14 The current output results
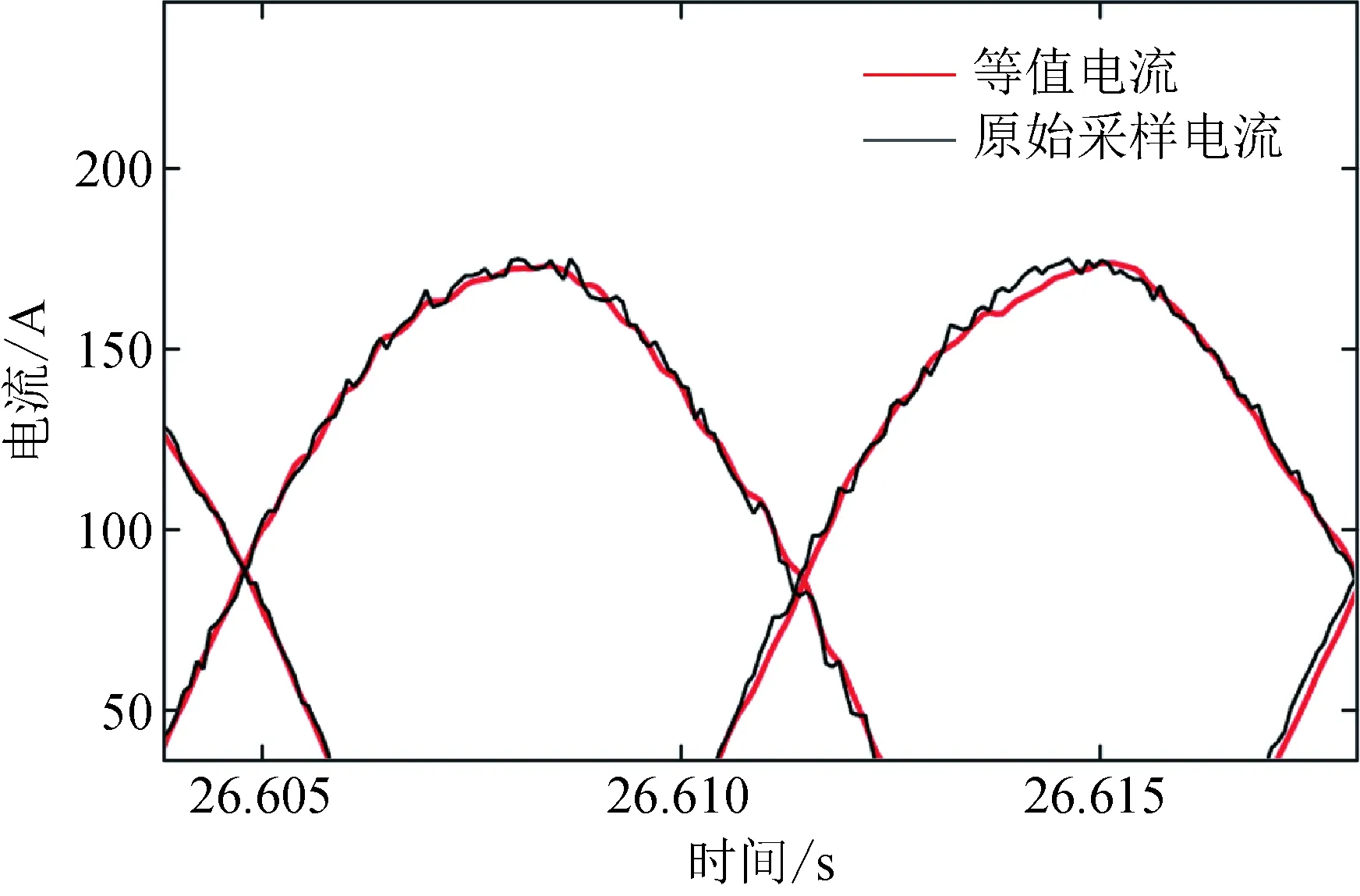
图15 电流输出结果局部放大Fig.15 The current output results are locally amplified

图16 电流输出结果对比Fig.16 Comparison of current output results
对比本文CDSI外部系统等值结果与未等值前采样获得的电流数据,其边界处三相电流曲线误差小于±1%,其拟合优度(R2)高于99%。在计算复杂性上,量测数据共计76 800×6个,SSI与本文CDSI方法计算速度相同,平均计算时间80~90 s。VF方法需要先进行等间隔采样,然后迭代求解超定线性方程组,计算量较大,速度较慢,平均计算时间超过1 000 s。
利用本文方法获得的外部系统电磁暂态等值模型具有很高的等值精度,解决了新能源机组型号多样、商业保密等原因造成的建模困难,同时也为后续故障还原、事故分析打下坚实基础。
5 结 论
本文针对以新能源为主体的新型电力系统,提出了一种基于CDSI的外部系统暂态等值方法。
1)利用本文方法将除故障外的其他部分划分为外部系统进行等效,可以缩短仿真耗时,加快仿真进程,高效准确地进行故障还原和事故分析。
2)CDSI利用输入和输出的全部信息获得系统状态空间模型,能够准确反映外部系统的频域特性,模型具有很高的等值精度,高于仅利用输出信息的SSI方法。
将电力系统进行外部系统等效后,下一步重点是解决内部系统模型等值,为故障还原、事故分析和扰动源定位等问题提供依据。

