基于蠕变损伤的深部泥质软岩巷道断面变化规律研究

王大顺

(中赟国际工程有限公司，河南 郑州 450007)

泥质软岩类的岩体流变特征显著，且往往会引发地下岩体工程结构出现稳定性问题，因此软岩巷道支护是影响矿山安全、有效生产的重要因素，也是工程上亟待解决的关键问题[1，2]。伽师矿自2003年开始采矿，已开采了近二十年，井下围岩多为紫红色含粉砂岩或浅绿色泥砂岩，岩体软弱易碎、遇水泥化、力学性能差，具有较强的遇水泥化崩解效应[3，4]。巷道表面围岩随着时间推移逐步被空气中的水分侵蚀丧失自承能力引发流态化破坏，且挤压立柱导致巷道变形，具有明显的流变时效属性。然而，对于泥质巷道的修复往往会落入“成巷—破坏—修复—再次破坏—再次修复”的恶性循环之中，从而降低矿井产出效率，同时对矿井工作人员人身安全也造成极大危害[5，6]。

近年来，国内学术界对于泥质围岩巷道变形失稳问题主要集中在宏观与微观两个层面上展开探讨。宏观层面，多是利用泥岩水化实验，探讨不同含水量的岩体对于施工过程力学系数的影响，以及水温、围压等外部因子对水化过程的影响作用。如魏海涛等人[7，8]通过测试矿岩物理力学性质和岩石泥质特征，研究泥质围岩相关力学特征和破环机理；刘宁等人[9]进行巷道岩体力学系数与水理性质实验，展现泥质软岩巷道破坏原理，提出“树脂锚杆+钢筋网+喷射混凝土”为核心的主动定向支护新工艺；李桂臣等人[10]通过物理模拟和数值模拟相结合的方法得出泥岩单轴抗压强度和弹性模量随黏性土含量的增加而增大的规律；YANG、Diansen[11，12]等人探究泥岩气体渗透性能、蠕变性质与含水率的联系。在微观层面，通过化学检测手段如离子色谱仪(SEM)、X-衍射等来测试水化过程泥岩内部矿物变化，或者软件模拟定性分析泥质围岩矿物组构对水化过程的影响。如张小刚等人[13]通过FLAC3D数值模拟方法探究深井软岩巷道的稳定性，提出拱形巷道可以提高安全性；刘高等人[14]研究高地应力软岩围岩的变形破坏机制，设计“锚网+喷射混凝土+钢支架”支护工艺；D.J.L.Guerra、Karaborni S、Nakano M等[15-17]利用分子模拟方法对粘土表面的吸附特性和粘土层间水的性质开展研究。上述研究成果对于研究软岩巷道变形有很好的指导作用，但是目前综合考虑损伤和围岩弱化系数的围岩蠕变本构、潮湿作用对泥质软岩变形的影响相关研究较少。本文以经典Cvisc本构模型为基础，建立了考虑损伤、围岩弱化系数的软岩本构模型，运用数值模拟、现场监测等综合方法验证了该本构模型的合理性，在此基础上对比分析了干燥状态、潮湿状态下的泥质软岩巷道围岩的蠕变范围及巷道断面变形规律，为现场支护设计提供依据，促进矿山安全、高效生产。

1 泥质软岩损伤本构模型建立

在施工过程中，巷道开挖瞬间会呈现出明显的弹性特性，而随着时间推移围岩含水量越来越大，变形模量、黏性等特性均会逐渐降低，泥质围岩由弹性特征转变为蠕变特性，泥质围岩流变特征呈现出非线性规律。经典流变模型能够较好地描述岩体部分蠕变特性，但均未能考虑岩体瞬时塑性变形及加速蠕变阶段变形，而深部环境下岩体一般具有衰减、匀速、加速蠕变的典型全蠕变阶段特征，李廷春等指出Cvisc模型是Burgers模型和Mohr-Coulomb模型的组合体[2]，其中，Burgers模型可以较好地描述蠕变过程中的黏弹性本构关系，Mohr-Coulomb模型可以较好地描述蠕变过程中的弹塑本构关系。Cvisc黏弹塑性模型如图1所示。

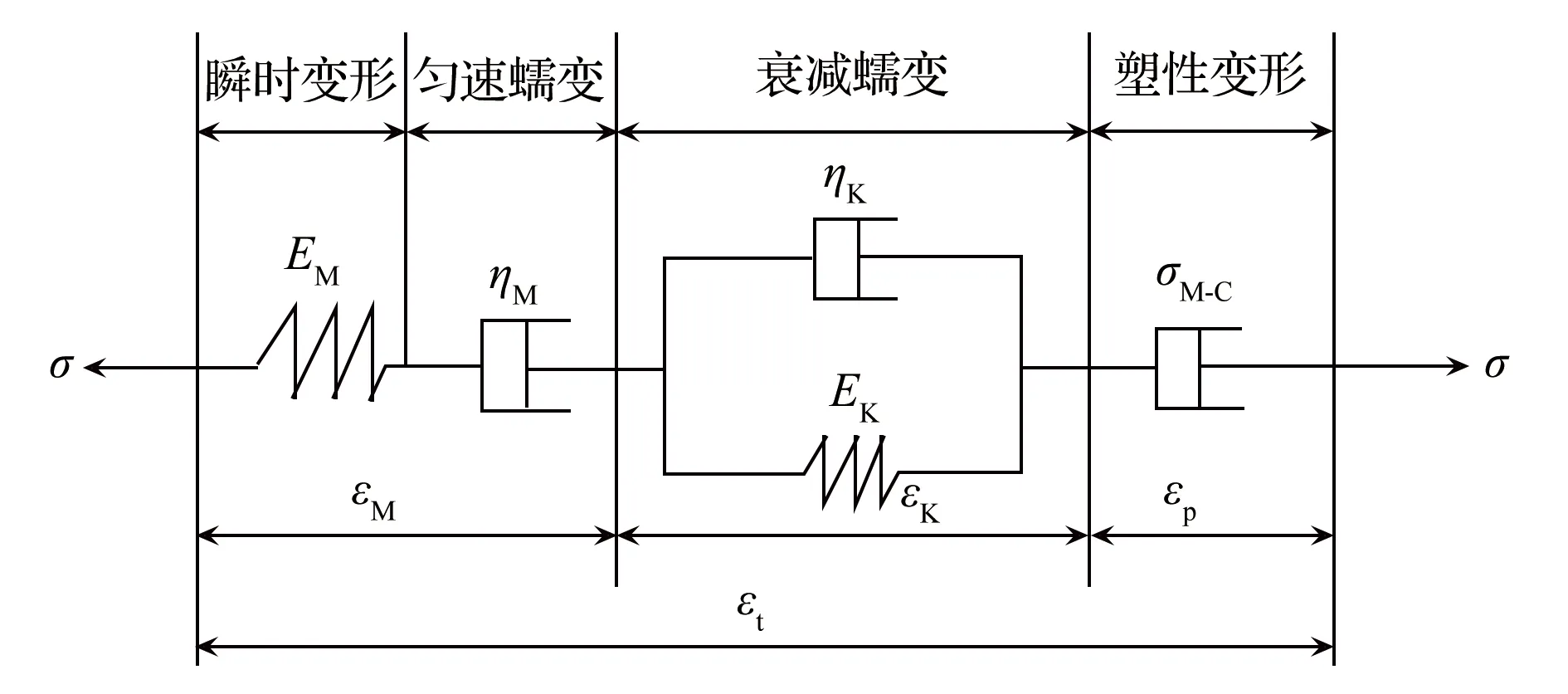
图1 Cvisc黏弹塑性模型

由图1可知，Cvisc黏弹塑性模型可以描述软岩蠕变阶段中的瞬时变形、衰减蠕变、匀速蠕变、塑性变形，其本构方程为：

式中，εt为总应变；ερ为塑性应变；σ为水平应力；t为时间；EM、ηM分别为Maxwell体的弹性模量和黏滞系数；EK、ηK分别为Kelvin体的弹性模量和黏滞系数。

软岩遇水泥化后的蠕变过程中，材料内部损伤程度及水环境对其变形影响较大，赵晶晶认为岩石损伤主要存在于蠕变过程中的加速蠕变阶段，且损伤变量Dt与时间t呈Weibull分布，其表达式为[18]：

Dt=1-e-αtβ

(2)

引入材料弱化系数λ考虑水环境对蠕变的影响，将λ引入式(1)可得蠕变过程中的瞬时变形、衰减蠕变、匀速蠕变、塑性变形阶段本构方程：

对Cvisc模型考虑损伤可描述加速蠕变阶段[19]，对式(1)中衰减蠕变、匀速蠕变、塑性变形的元件考虑损伤，损伤的Cvisc黏弹塑性模型如图2所示。

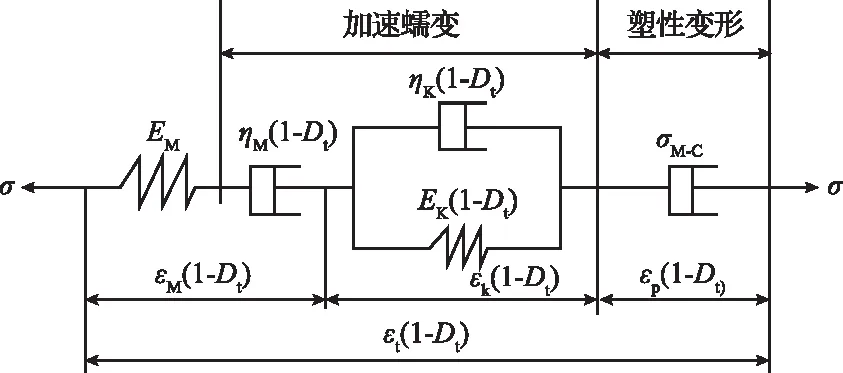
图2 损伤的Cvisc黏弹塑性模型

由有效应力模型和应变等价原理并联立式(2)、式(3)可得蠕变过程中的加速蠕变阶段本构方程为：

式(3)、式(4)描述了岩体蠕变全过程(瞬时变形、衰减蠕变、匀速蠕变、加速蠕变、塑性变形)阶段的本构方程，且考虑了岩石损伤变量Dt、材料弱化系数λ对蠕变的影响，从而更好地揭示围岩随时间弱化的情况及损伤破坏规律。

2 泥质软岩巷道变形破坏数值分析

2.1 模型建立

伽师矿开采深度达600 m，巷道围岩具有层理发育、强度低、遇水易泥化等特征[20]，根据该矿地质资料，运用UDEC离散元建立深部巷道二维平面应变计算模型如图3所示，为消除边界效应对模型计算的影响，将模型长与高均设置为5倍洞径大(30 m)，监测点分别位于拱顶、左帮和右帮深处0.3 m。

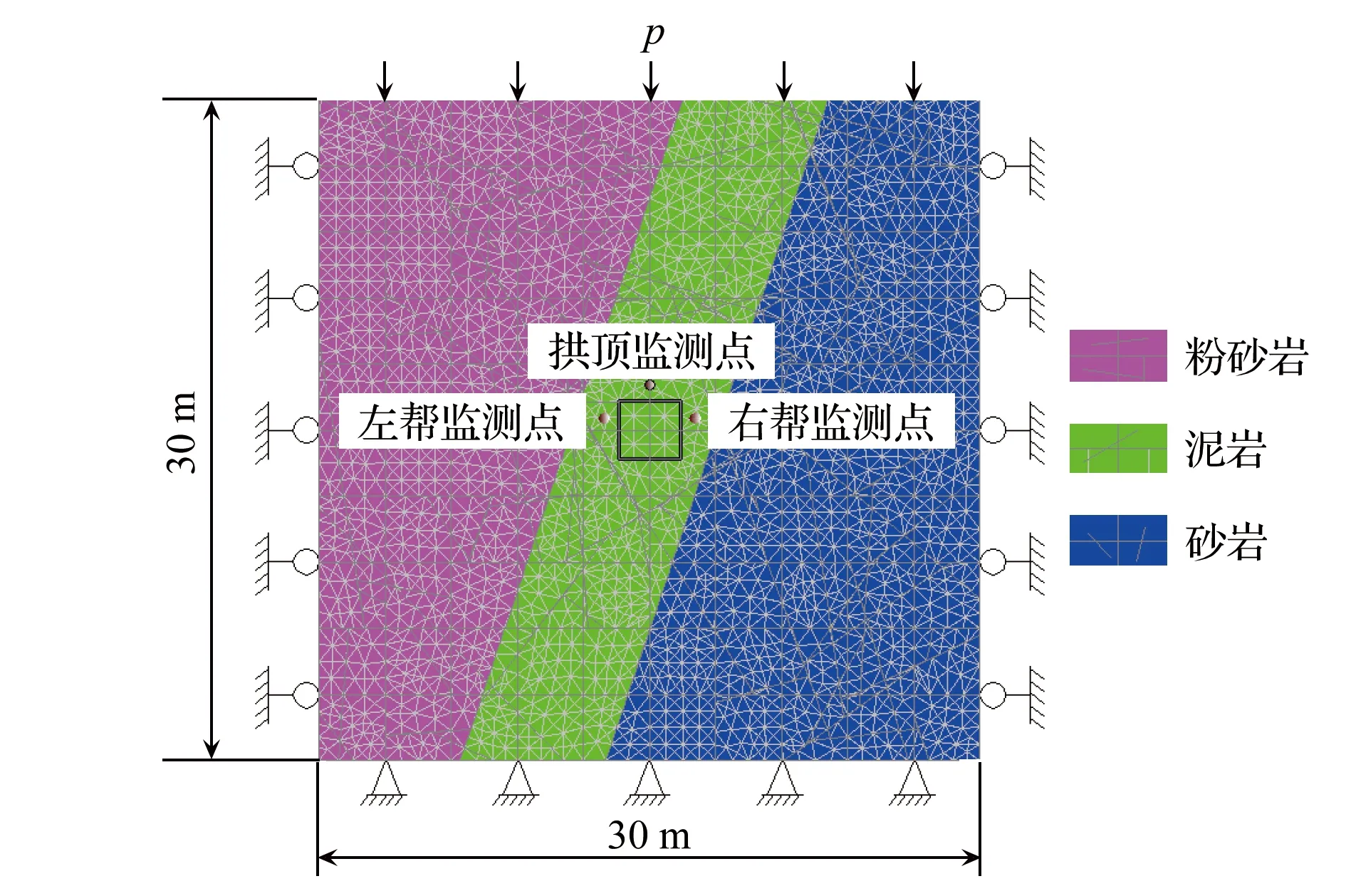
图3 巷道数值模型

模型上方施加压力为p=γh，其中，γ为模型上方岩层平均容重，水平方向施加水平应力为μp(μ为0.42)，模型左、右两侧限制水平位移，底部限制垂直位移。模型中通过蒙特卡罗法生成符合该矿地质勘察结果的随机裂隙和防止模型计算自动删除孤立随机裂隙的水平和垂直裂隙[21]。折减后的巷道围岩物理力学参数见表1。

表1 巷道围岩物理力学参数

2.2 模型蠕变参数反演

较准确的数值计算参数是数值模型计算的前提，BP神经网络可实现输入参数和目标参数的任意非线性关系，可通过调整初始权重及阀值获得满足精度要求的预测目标参数[22]。为尽可能还原巷道围岩性质，数值模型计算中巷道所在的泥岩采用Cvisc本构模型，其余岩层采用Mohr-Coulomb本构模型[23]，最终以数值计算的监测点位移与实际监测位移的均方差作为输入集体，将蠕变参数EM、ηM、EK、ηK作为输出集运用BP神经网络进行预测，直到满足精度要求。数值计算结果与实际监测结果对比如图4所示。分析图4可知，数值计算结果与现场实际监测结果吻合度较高，证明反演的参数能够较准确地反映现场巷道围岩的变形情况，最终反演得到参数见表2。

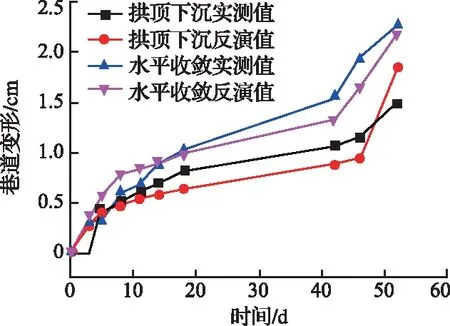
图4 数值计算结果与现场实际监测结果对比

表2 巷道围岩蠕变参数

3 计算结果分析

伽师矿巷道所在岩层多为砂岩和泥岩，魏海涛等利用单轴压缩实验得到砂岩和泥岩的软化系数为0.12～0.21，说明深部环境巷道围岩强度受水的影响较大[7]。由于该矿在巷道掘进过程中已经采取相应地下水防控措施，本文考虑水对泥岩强度影响时采用泥岩软化系数0.21对其强度进行弱化。应用2.1节数值模型建立干燥状态下和潮湿状态下的数值模型，对比分析干燥状态下和潮湿状态下巷道围岩蠕变范围变形规律。

3.1 验证本构模型

将2.2节反演的蠕变参数应用到干燥状态下和潮湿状态下数值模型计算中，干燥状态下围岩材料弱化系数λ取0，潮湿状态下围岩材料弱化系数λ取0.21。巷道开挖稳定后对巷道左帮、拱顶、右帮的应变及时间进行监测，监测所得的数据采用式(4)进行拟合，其中，式(4)应力水平为各时间段平均应力，干燥状态下拟合的主要参数见表3，拟合的结果如图5所示。

表3 干燥状态下式(4)拟合参数

图5 干燥状态下数值监测数据与理论分析的关系

分析表3可知蠕变参数EM、ηM、EK、ηK与表2的参数数量级基本一致，说明式(4)可以较准确地描述软弱围岩干燥状态下变形与时间的关系，拱顶、左帮、右帮的塑性变形εp均较小，说明干燥状态下软弱围岩蠕变阶段主要发生黏弹性变形。

采用式(4)软化状态下拟合的主要参数见表4，拟合的结果如图6所示。分析表4可知，蠕变参数EM、ηM、EK、ηK与表2的参数数量级也基本一致，说明式(4)可以较准确地描述软弱围岩软化状态下变形与时间的关系，拱顶、左帮、右帮的塑性变形εp均小于干燥状态下，说明软化状态下围岩含水量增加导致围岩在蠕变阶段中黏弹性变形更明显，使得最终围岩的变形大于干燥状态下的变形。

表4 软弱状态下式(4)拟合参数

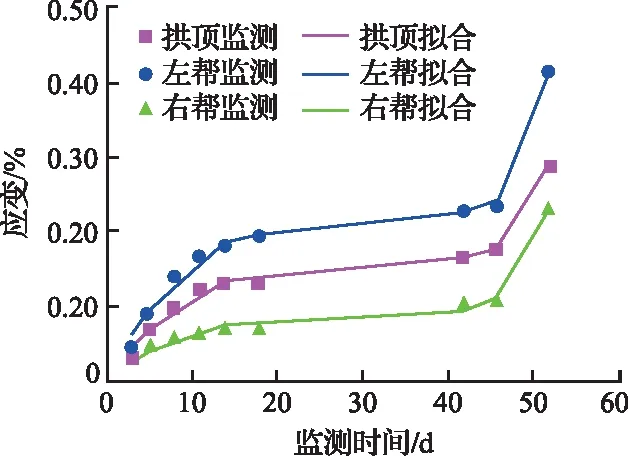
图6 潮湿软化状态下数值监测数据与理论分析的关系

分析图5、图6可知，干燥状态下和潮湿软化状态下的监测数据采用式(4)进行拟合的效果较好，潮湿软化状态下拱顶、左帮、右帮最大应变为0.29%、0.41%、0.23%，干燥状态下拱顶、左帮、右帮最大应变为0.3%、0.35%、0.21%，说明围岩遇水潮湿对倾斜地层巷道左帮影响较大，对拱顶、右帮影响较小。干燥、潮湿软化状态下不同位置围岩蠕变随着时间的增加均呈现典型的蠕变减速(3～18 d)、蠕变匀速(18～46 d)、蠕变加速(46～52 d)三个阶段。

干燥、潮湿软化状态下不同阶段围岩蠕变速率见表5，分析表5可知，干燥状态下不同位置围岩在蠕变匀速、加速阶段的平均蠕变速率为减速阶段的0.2～0.5、4.4～6.4倍，潮湿软化状态下围岩在匀速、加速阶段的平均蠕变速率为减速阶段的0.14～0.46、2.8～7.9倍，说明围岩蠕变时潮湿软化状态下相比干燥状态下蠕变匀速阶段历时延长，加速阶段时间缩短，最终导致蠕变匀速阶段潮湿软化状态下围岩积累的损伤更多，促使在蠕变加速阶段较快地发生变形，此阶段对围岩的破坏性也更大。

3.2 围岩蠕变范围确定

深部三高环境下巷道开挖稳定后围岩发生蠕变，促使巷道断面逐渐变形。由前文分析可得巷道两帮水平收敛变形大于拱顶的下沉变形，干燥和潮湿软化状态下不同时间段巷道围岩的水平位移如图7所示。

表5 干燥、潮湿软化状态下不同阶段围岩蠕变速率

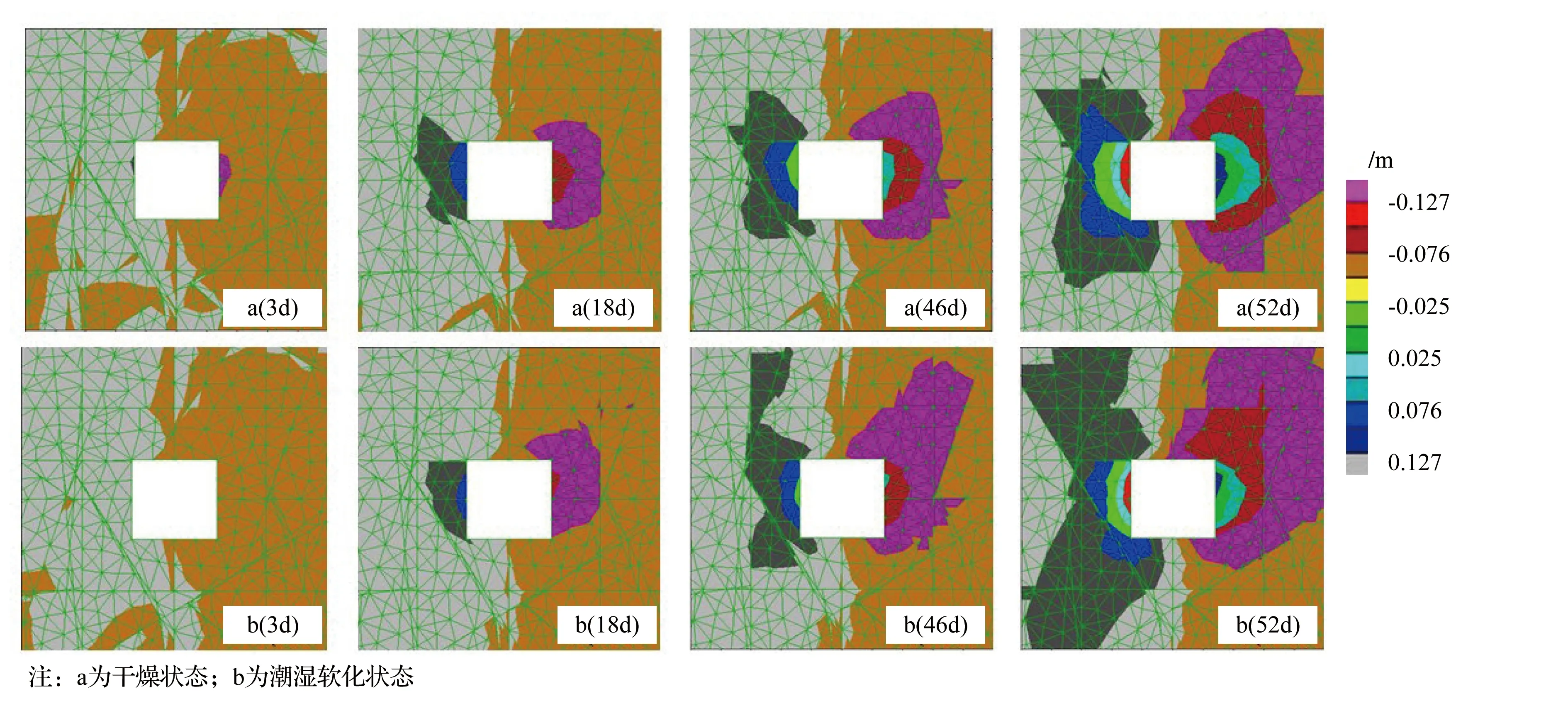
图7 不同状态下巷道围岩水平位移

分析图7可知，随着蠕变时间延长水平位移影响范围逐渐增大，3～18 d时围岩水平位移影响范围较小，且干燥、潮湿软化状态下影响范围基本一致，说明两种状态下3～18 d围岩均变形缓慢，此阶段围岩变形与围岩软化状态关系不大；18～46 d时水平位移影响范围逐渐增大，且潮湿软化状态下水平位移影响范围略大于干燥状态下，说明潮湿软化状态下围岩损伤略大于干燥状态下，此阶段围岩变形与围岩潮湿软化状态为正相关关系；46～52 d时围岩水平位移范围增大较多，且潮湿软化状态下水平位移范围大于干燥状态下，说明潮湿软化状态下围岩损伤大于干燥状态下，导致围岩发生相同的变形历时缩短，此阶段围岩变形与围岩潮湿软化状态为正相关关系。以上分析说明围岩软化后虽然会导致围岩变形量增大，但潮湿软化状态对围岩的损伤具有明显的时间效应，在某个时间之后潮湿软化状态对围岩的损伤效果会更明显。

干燥状态下巷道围岩左侧不同深处围岩水平位移和时间关系如图8所示，巷道围岩变形小于0.02 mm/d时可认为基本稳定[24]，由图5、图6可知，46 d以后围岩处于蠕变加速阶段，因此，以46 d内围岩变形速度均为0.02 mm/d(累计水平位移为0.00092 m)为界对围岩蠕变范围进行区分。

分析图8可知水平位移与时间为正比例关系，与深度为反比例关系，且左侧围岩深度1.0～5.5 m范围内围岩累计水平位移大于0.00092 m，因此认为巷道左侧围岩的蠕变范围为1.0～5.5 m。同理可分析得出干燥状态下巷道右侧、上方、下方围岩的蠕变范围为1.0～4.5 m、1.0～5.0 m和1.0～3.5 m，由此可知干燥状态下围岩蠕变范围具有非对称性，且总体范围从巷道左侧围岩顺时针依次减小。

潮湿软化状态下巷道左侧、右侧、上方、下方围岩的蠕变范围为1.0～5.5 m、1.0～4.5 m、1.0～5.5 m和1.0～4.0 m，说明潮湿软化状态下围岩蠕变范围特征与干燥状态下较一致，但潮湿软化状态下的围岩蠕变范围大于干燥状态下的蠕变范围。

3.3 巷道断面变形分析

巷道围岩蠕变促使巷道断面发生缩减，其形状也与原设计产生偏差从而影响巷道正常基本功能。干燥和潮湿软化状态下矩形巷道断面在不同时间段内主要监测点的在水平和垂直方向相对水平位移与时间的变化关系如图9所示。分析图9可知，水平相对位移为-1.5～1.5 cm(-1.2～1.6 cm)，垂直方向相对位移为-2.2～1.5 cm(-2.5～1.6 cm)，各监测点相对位移与时间为正比例关系，d监测点以垂直相对位移为主，造成巷道底鼓；b、f监测点以水平相对位移为主，且b点水平位移大于f点，造成巷道左侧片帮大于右侧；a、c、e、g、 h监测点既发生水平相对位移也发生垂直相对位移，造成巷道断面向内缩减；b、f、h、d监测点的相对位移对巷道断面变化影响较大，造成整体巷道断面变化具有非对称性，且变化形状由偏转的近似菱形过渡为梯形，最终巷道断面形状与文献[25]基本一致。巷道在3～46 d干燥(潮湿软化)状态下倾斜地层巷道断面相对位移较接近，46～52 d潮湿软化状态下促进围岩变形导致围岩最终变形大于干燥状态下，说明只有经过一定的时间，潮湿软化状态才能加剧围岩的变形内部损伤进而加剧围岩变形。

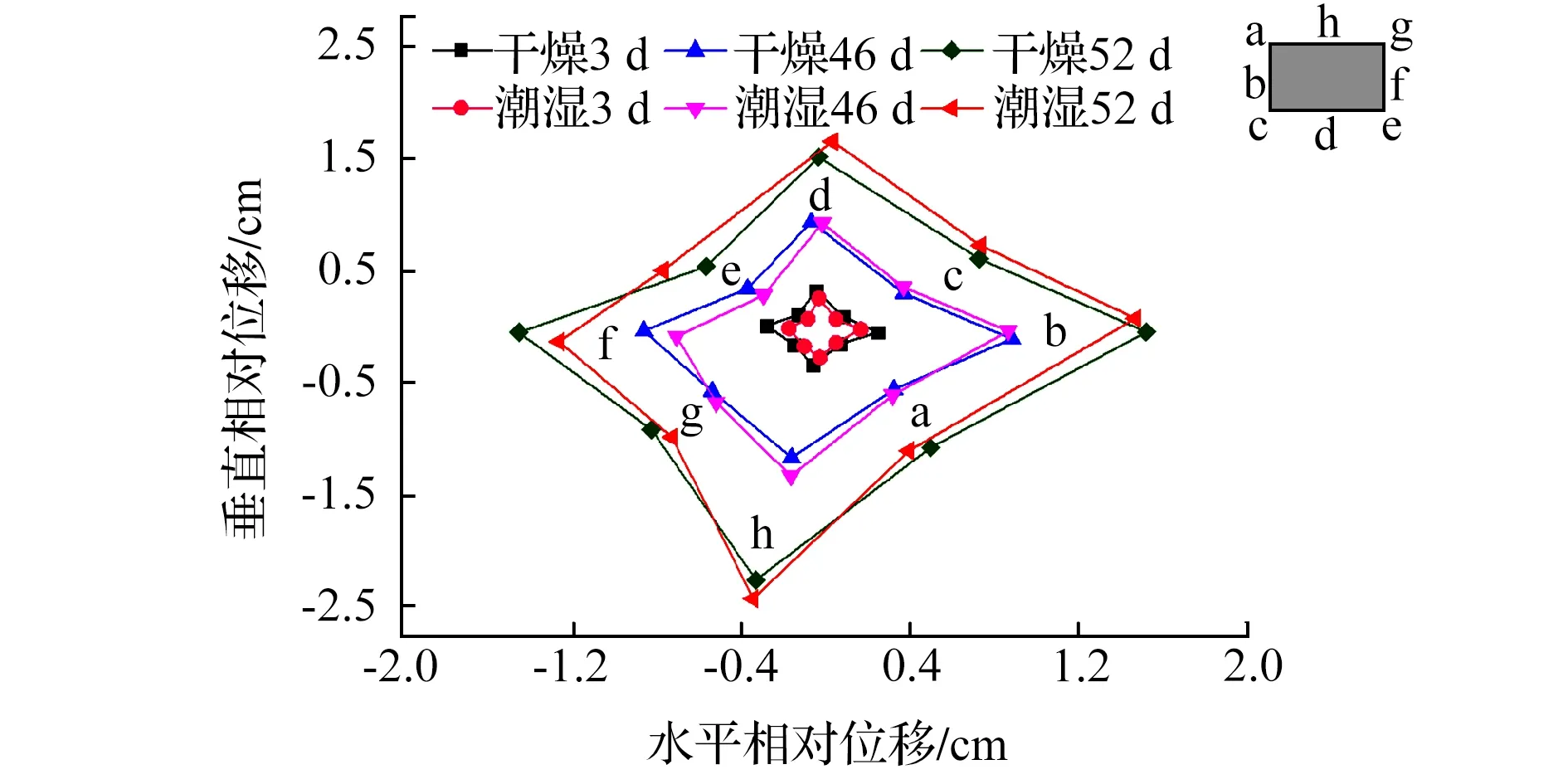
图9 干燥、潮湿软化状态下不同时间巷道断面相对位移

4 结 论

1)泥质围岩具有明显的流变时效属性，属于典型的结构性流变岩体。泥质围岩多为粉砂岩或泥砂岩，当其处于不利地质条件，如巷道表面围岩逐步被空气中水分侵蚀、遇水泥化、崩解等，会伴随着时间丧失自承能力发生蠕变破坏，这种状态下立柱易被挤压发生巷道变形破坏。

2)考虑损伤、围岩材料弱化系数的Cvisc本构模型可以较好地描述深部环境下巷道围岩变形与时间的关系，围岩在蠕变阶段中主要表现为黏弹性变形。

3)3～18 d时干燥状态和潮湿软化状态下围岩蠕变基本相同，18 d以后潮湿软化状态下蠕变范围较干燥状态下扩大，潮湿软化状态下围岩的损伤具有明显的时间效应。

4)干燥(潮湿软化)状态下左侧、上方、右侧、下方围岩的蠕变最大范围为5.5，5.0，4.5，3.5 m(5.5，5.5，4.5，4.0 m)，蠕变总体范围具有非对称性，从巷道左侧顺时针依次减小。

5)倾斜地层深埋巷道断面相对变化均具有非对称性，且在46～52 d潮湿软化状态下促进围岩变形导致围岩最终变形大于干燥状态下。