基于LHS-CPSE的非侵入式边坡可靠性分析方法及其应用

郭文礼

(兰州有色冶金设计研究院有限公司, 兰州 730000)

在房建工程、公路工程、铁路工程等建设过程中,不可避免地遇到边坡稳定性问题,如高路堤边坡、深路堑边坡等[1-3]。目前,主要采用极限平衡法求解边坡稳定性,并借助单一安全系数表征其稳定程度[4]。但在实际工程中,部分安全系数满足设计要求时边坡也出现了失稳破坏,其关键原因之一是未考虑岩土体的不确定性。因此,顾及岩土变异性的边坡稳定性分析已成为工程界岩土领域的研究热点。此外,单一安全系数法也很难与国际接轨,以可靠度理论为基础的极限状态设计法将是边坡设计的发展方向[5]。

传统的可靠度分析方法主要是通过经验和力学公式建立显式功能函数,进而求解工程的可靠度或失效概率,如中心点法、验算点法和当量正态化法等[6]。在简单、非线性程度低的工程结构中,传统可靠度分析法能够得到较为满意的结果。然而,岩土工程的变异性和高非线性导致其很难通过经验或者力学公式准确表达其极限状态函数,这势必会影响可靠度分析结果的准确性。因此,随机有限元应运而生,比较典型的有直接Monte-Carlo随机有限元法[7]、泰勒展开随机有限元法[8]、摄动随机有限元法[9]、纽曼扩展Monte-Carlo随机有限元法[10]和谱随机有限元[11],这些方法有效地解决了复杂环境下岩土工程可靠性问题,但其抽样次数巨大或者需要修改确定有限元程序,且对随机变量的分布有严格要求。为了解决上述问题,非侵入式有限元得到了快速发展,该方法无需对确定有限元与可靠性计算进行相互耦合,一方面降低了计算的复杂性,另一方面有效提高了计算速率。此外,如果配合适合的抽样技术,将会进一步减少非侵入式有限分析法的计算量,进而大幅提高计算效率。

基于上述思路,现提出一种基于拉丁超立方抽样-切比雪夫多项式随机展开模型(Latin hypercube sampling-Chebyshev polynomial stochastic expansion,LHS-CPSE)的非侵入式边坡可靠性分析方法,该方法采用拉丁超立方抽样技术(LHS)抽取岩土体的原始样本,基于切比雪夫多项式随机展开模型(CPSE)建立显式响应面模型,借助蒙特卡洛法(Monte Carlo,MC)计算边坡的可靠度,在兼顾准确性的同时,有效提高计算效率,快速地为工程设计和决策提供指导。同时,以兰州市盐什公路的一段边坡为工程案例,将其计算结果与直接蒙特卡洛法进行对比,验证新方法的可靠性,并将其应用在坡体开挖方案决策中。

1 LHS-CPSE非侵入可靠度模型

1.1 有限元折减强度法

极限平衡法与有限强度折减法是边坡稳定性分析中的常用方法,与前者相比,后者不仅顾及了土体的弹塑性本构关系影响,而且还能较好地模拟坡体失稳过程和滑面的形状。有限元强度折减法的主要思路是:将所要研究的边坡岩土体强度指标按照一定的原则进行折减,直到边坡发生失稳破坏,并将临界破坏的强度折减系数作为边坡安全系数[11-12]。折减前、后的土体强度指标之间的关系如下。

cs=c/Fs

(1)

tanφs=tanφ/Fs

(2)

式中:c、cs分别为折减前、后边坡岩土体的黏聚力;φ、φs分别为折减前、后边坡岩土体的内摩擦角;Fs为折减系数,即安全系数。

1.2 岩土屈服准则

岩土体作为一种天然材料,其工程特性十分复杂,岩土屈服准则虽多,但没有一个屈服准则能够准确描述岩土的各种工程性质。其中,摩尔-库伦(MC)屈服准则是工程中应用最广、最多的一种屈服准,但其在π平面上为不规则的六边形,其棱角处为奇异点,为了消除这种影响,Drucker和Prager在Mises准则的基础上进行改进,得到屈服准则,即DP屈服准则[13],其表达式如下。

(3)

I1=σ1+σ2+σ3

(4)

(5)

式中:I1为第一应变不变量;J2为第二偏应力不变量;Fs为折减系数;σ1、σ2、σ3分别为第一、第二、第三主应力;α、β为岩土材料常数。

1.3 拉丁超立方随机抽样

拉丁超立方随机抽样(LHS)最早由McKay等[14]提出,属于多维分层抽样范畴。LHS得到的样本点不仅具有均匀分层特性,而且还能在大幅度减小样本数量的情况下兼顾尾部样本点,抽样效率明显高于普通的抽样方法。LHS抽样流程如下。

步骤1根据研究对象的特点,合理确定抽取的样本数量m。

步骤2将随每个随机变量Xi(i=1,2,…,n)的分布函数均分为m段,即保证每段的概率相等且不重叠。

步骤3在每段随机选取一个样本点,组成m×n的样本矩阵。

步骤4将各随机变量的m个样本随机组合,得到输入变量的样本向量。

图1为具有2个随机变量(即n=2)的拉丁超立方随机抽样原理,其中抽取的样本数量m=5。

图1 随机变量X1和X2分层抽样和LHS抽样Fig.1 Stratified sampling and LHS sampling of random variables X1 and X2

1.4 响应面模型建立

响应面实质上是输入变量与响应变量之间建立的一种近似函数关系。目前,近似函数大多采用通用多项式进行拟合,然而它在拟合高度非线性关系时会出现病态问题。为了解决这一问题,本文采用切比雪夫多项式随机展开模型(CPSE)[15]拟合安全系数Fs与输入变量x之间的显式函数关系式。

CPSE正交的递推关系如下。

(6)

基于该正交基的显示表达式为

(7)

式(7)中:xi1、xi2、xi3、…、xin为随机变量;Sn(xi1,xi2,…,xin)为n阶CPSE多项式;c0、ci1、ci1i2、…、ci1i2…in为待定系数,展开到n阶时,待定系数个数为

Nc=(n+p)!/(n!+p!)

(8)

将拉丁超立方随机抽样产生的m组随机变量通过Nataf正态变换法转化为标准正态随机变量[16],并代入到确定有限元,利用折减系数法得到m组安全系数Fs=[Fs1,Fs2,Fs3,…,Fsm]T,再将其代入式(7),可得到线性方程组为

HC=Fs

(9)

式(9)中:H为m×Nc维系数矩阵;C为待定系数矩阵。

利用最小二乘法,可求解待定系数矩阵C中各元素,即c0、ci1、ci1i2、…、ci1i2…in等,进而利用显示函数表征随机变量与安全系数的关系,最终建立边坡稳定性功能函数为

Fs-L=0

(10)

式(10)中:L为边坡设计安全系数,可参考相关规范的相关内容进行取值,取为1.0。

2 计算流程

传统的可靠度分析方法,主要根据经验或者力学公式构建显式功能函数,进而求解工程的可靠度,在简单、近似线性的工程结构中被广泛应用。侵入式随机有限分析虽然可求解复杂的非线性工程的可靠度,但大多需要对确定性有限元程序进行改写,且计算流程烦琐、计算量巨大。而非侵入式随机有限元法,无需将可靠性计算与确定有限元进行相互耦合,不仅降低了求解难度,而且明显提高了分析效率。

利用Python语言编制相关程序,并导入ABAQUS软件中进行边坡可靠度分析,其计算流程如图2所示。

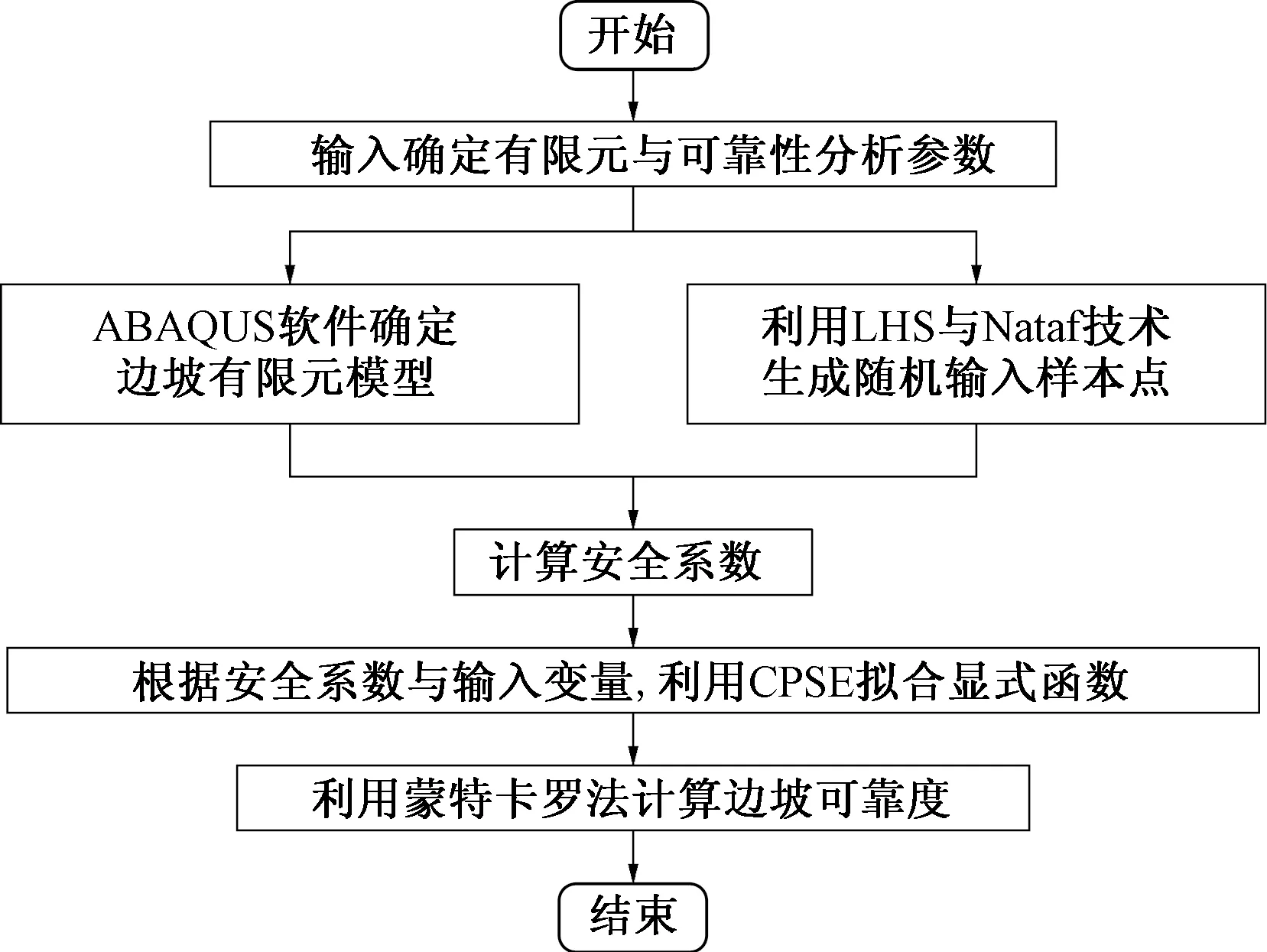
图2 基于LHS-CPSE的非侵入可靠度分析流程Fig.2 Flow of non-intrusive reliability analysis based on LHS-CPSE

3 算例与验证

选取兰州市盐什公路项目K13+025～K13+380段黄土边坡为研究案例(图3),地质勘察发现,边坡以晚更新世黄土为主,土质均匀,以粉粒为主,结构疏松,具大孔隙,摇震反应迅速,无光泽,切面粗糙,干强度低、韧性低,稍湿、稍密,其强度指标统计参数如表1所示。边坡高度29.1 m,按照坡面倾角的不同,大致划分为上、中、下3段,倾角从下到上依次为67°、48°和35°(图4)。修建公路时,部分边坡需要开挖。

表1 边坡土体强度指标统计参数Table 1 Statistical parameters for strength indicators of slope soils

图3 边坡现场照片Fig.3 Photo of the slope

图4 边坡剖面图Fig.4 Slope profile

图5为按照图4所建的确定性有限元模型示意图,网格单元为4节点平面应变单元,左侧为位移约束(水平方向为0),底部为固定约束,并在所有单元施加重力荷载。

图5 确定性有限元模型示意图Fig.5 Schematic diagram of the deterministic finite element model

可靠性分析中,其结果的准确性一般采用蒙特卡洛法(MC)进行验证,表2给2阶LHS-CPSE法、3阶LHS-CPSE法以及MC法的可靠度。可以看出,3种方法的计算结果非常接近,可靠度均在95%左右,但3阶LHS-CPSE法更接近MC法,误差仅为0.15%,这表明LHS-CPSE法准确可靠,可以作为边坡可靠度分析的一种新思路。此外,与MC法相比,2阶LHS-CPSE法、3阶LHS-CPSE法显著的降低了计算时间,前者的计算时间为1 536 min,后两者分别为28 min和77 min,分别为MC法计算时间的 0.02倍和0.05倍,这反映出LHS-CPSE法计算的高效性。值得注意的是, 2阶LHS-CPSE法与3阶LHS-CPSE法误差仅为0.23%,但前者的计算时间约为后者的1/3,综合精度和效率,建议采用2阶LHS-CPSE法。

表2 可靠度计算结果对比Table 2 Comparison of reliability calculations

4 开挖对边坡可靠度的影响

如图6所示,为减小坡体开挖量V,进而节约工程造价,结合现场地质勘察资料,开挖后初步设计为三级边坡,且各级坡面尽量与原坡面平行,以工况1为例,Ⅰ级边坡和Ⅱ级边坡的坡度设计为1∶0.5,Ⅲ级边坡坡度设计为1∶1。 为增加边坡开挖后的稳定性,在相邻两级边坡之间设置边坡平台,Ⅱ级边坡平台(蓝色线)设计宽度为2.0 m,Ⅰ级边坡平台(粉红色线)宽度设计为7种工况(即L=3.0、3.5、4.0、4.5、5.5、5.5、6.0 m),进一步探讨其对边坡稳定性和可靠度的影响。

图6 开挖方案Fig.6 Excavation scheme

图7反映了Ⅰ级边坡平台宽度(简称平台宽度)对其平均安全系数的影响,可以观察到,随着平台宽度的增加,平均安全系数呈显著的递增趋势,从宽度3.0 m的1.05增加至6.0 m的1.42,增幅达35.2%。这说明边坡的平均安全系数与平台宽度呈正相关,可以通过增大其宽度来提高坡体的稳定性,平台宽度增加导致其上部土体质量减小是其稳定性提高的关键原因之一,即平台宽度增加相当于对边坡上部进行减载(当平台宽度从3.0 m增加至6.0 m时,其上方的土体体积减小52 m3/m),致使其下滑力减少,间接增加边坡的稳定性。

图7 平台宽度与平均安全系数的关系曲线Fig.7 Curve of platform width versus average safety factor

图8为不同平台宽度条件下边坡的可靠度,很明显,随着平台宽度的增加,边坡的可靠度呈“先急剧增大,再趋于稳定”的态势。当平台宽度从3.0 m增加至4.5 m时,可靠度从81.5%增加至99.5%,增幅约为22%;平台宽度从5.0 m至6.0 m,可靠度达到100%,即此时边坡稳定性失效概率为0。

图8 平台宽度与可靠度的关系曲线Fig.8 Curve of platform width versus reliability

综上所述,随着平台宽度的增加,坡体开挖量和稳定性呈递增趋势,但可靠度先急剧增大后趋于稳定,即平台宽度从3.0 m增加至4.5 m时,宽度增加对其可靠度影响显著,但超过4.5 m后,宽度增加对可靠度的影响非常小。兼顾工程造价与安全考虑,其边坡平台按照4.5 m设计较为合理,此时平均安全系数为1.26,失效概率仅为0.5%。

5 结论

(1)LHS-CPSE法采用拉丁超立方抽样技术(LHS)抽取岩土体的原始样本,基于切比雪夫多项式随机展开模型(CPSE)建立响应面模型,借助蒙特卡洛法(MC)计算边坡的可靠度。

(2)LHS-CPSE法与直接蒙特卡洛法结果非常接近,其误差不到0.5%,且计算时间大幅度缩减,验证了该方法的可靠性和高效性。

(3)3阶CPSE随机展开模型较2阶CPSE随机展开模型计算精度略高0.23%,但前者的计算效率是后者的1/3,兼顾精度和效率推荐采用2阶 CPSE随机展开模型。

(4)随着Ⅰ级边坡平台宽度的增加,开挖量与边坡平均安全系数呈递增趋势,但可靠度呈“先急剧增大,再趋于稳定”的态势,兼顾工程造价与安全考虑,其边坡平台按照4.5 m设计较为合理。

(5)LHS-CPSE法能够快速准确地计算边坡的可靠度,可以为公路边坡设计和决策提供技术支撑。