岩溶隧道道床上浮机制及底鼓特征数值分析
杨辉, 裴俊豪, 朱吉斌, 刘宁*
(1.中交一公局集团有限公司, 北京 100024; 2.贵州大学土木工程学院, 贵阳 550025)
中国城市轨道交通运营总里程约7 655 km(截至2020年12月31日),通车城市43个,通车线路共246条[1]。然而,无砟道床普遍应用于轨道交通隧道中,随着轨道交通隧道的蓬勃发展,岩溶发育地区突水危害风险高[2],发生无砟道床上浮变形现象也并不鲜见。众所周知,无砟道床对变形要求更为严格,当列车高速运行时,道床上浮引起的轨道不平顺可能导致列车脱轨或翻车等重大交通事故。
仰拱底鼓是引起无砟道床上浮的一个重要原因,多年来已进行了大量研究来解决这一问题。Wang等[3]运用数值模拟与现场监测数据对比分析,提出岩层倾角是造成巷道底鼓的主导因素,其他因素只能影响底鼓的程度。Sun等[4]采用红外热像仪和摄像机捕捉巷道断面的热响应和位移,发现水平应力对底鼓破坏影响很大,岩体破坏关联其温度异常变化。Ma等[5]基于离散元数值计算的理论分析,发现层状围岩夹层连接的弱化(包括失效)是仰拱底鼓的一个重要促成因素,仰拱深度增加可抑制底鼓。Tang等[6]、Du等[7]在隧道仰拱底部存在膨胀围岩的案例中,研究总结了围岩在潮湿环境下发生膨胀引发仰拱底鼓的变形规律与受力情况。钟祖良等[8]通过现场勘察分析隧道底鼓影响因素,包括隧道底板岩层压曲失稳,软岩遇水软化、膨胀和流变等。Taylor等[9]提出地震引起的土壤液化会导致隧道等轻质地下结构的漂浮破坏,并通过振动台试验得出隧道下方进行的地层改良在减少隆起方面最为有效。Mo等[10]利用数值分析与数值模拟研究煤矿巷道底鼓机理,得出上覆强底板岩层之下的弱底板单元的破坏似乎诱发了底板的向上运动。路军富等[11]基于隧道底鼓变形实测数据,结合岩体蠕变参数识别方法,预测岩体蠕变引起的隧道底鼓。Zhao等[12]通过现场监测与数值模拟分析,发现仰拱底鼓一般发生在深埋隧道段,并提出了一种可有效减小深埋隧道仰拱底鼓引发道床变形的新型预留槽仰拱结构。Sun等[13]利用有限差分软件对底板和巷道两侧开槽进行了数值模拟,得出选择合适的切削参数可以提高软岩巷道底鼓的控制效果。Yu等[14]提出高应力软岩巷道“分步联合、分级加固”的抗底鼓支护技术,并给出了锚索和锚杆参数校核的设计方法。Li等[15]在总结国内外隧道排水结构形式的同时,提出一种新型仰拱底部排水降压措施,抑制仰拱基底水压力,控制仰拱与道床变形量。除了交通隧道,大量研究人员还研究了煤矿底板隆起的机理和控制技术,提出了帮部加强锚索支护、滞后注浆、底板切槽等措施,可有效减小巷道底板上浮[16-18]。
众多学者已对仰拱底鼓进行了大量研究,虽然仰拱底鼓会进一步影响道床上浮变形,但底鼓问题主要发生在处于施工阶段的深埋隧道,对于已建成轨道交通隧道发生无砟道床上浮的特征和处治措施研究却很少。并且现有研究主要集中于深埋隧道的围岩地质构造与围岩岩性对仰拱底鼓的影响,以及地震产生的岩土液化对隧道等轻型结构的影响。但随着岩溶发育地区城市轨道交通的迅速发展,埋深较浅的非地震带轨道交通隧道也频繁发生无砟道床上浮现象。针对这一问题,现结合案例进行探讨,发现地下水是引起岩溶地区轨道交通隧道无砟道床上浮的主要原因。采用理论分析结合数值模拟,对比分析正常运营、仰拱与仰拱填充层裂隙渗水、仰拱与仰拱填充层裂隙渗水且道床水平脱空、仰拱与仰拱填充层裂隙渗水且道床纵向脱空4种工况。研究在地下水影响下轨道交通无砟道床的上浮特征,提出地下水引起道床上浮的曲线公式,并总结提出预防与处治无砟道床上浮的相关措施。
1 隧道衬砌水压力计算
隧道工程防排水体系设置方法不同,其防排水结构类型主要分为:全包式防水,半包式防水。其中全包式防水隧道衬砌承受地下水的水压力。衬砌水压不仅关联地下水位、围岩性质和防水结构类型,也是获取道床与仰拱填充面间的水压力的关键,如图1所示。
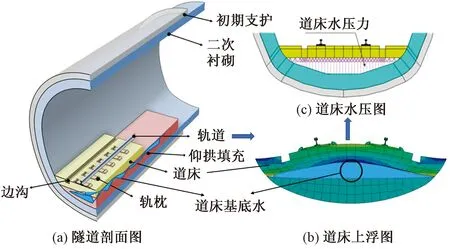
图1 道床水压脱空示意图Fig.1 Schematic diagram of ballast water pressure vacation
因此,采用理论计算方法对全包式防水隧道衬砌外水压力值进行分析[19],隧道水压力公式推导基本假定如下。
(1)假设隧道为深埋隧道,可将隧道、衬砌、围岩及注浆层等效为圆形。
(2)围岩为各向同性。
(3)地下水水位稳定,水层均质、各向同性的渗流体视为无限延伸。
(4)水流服从达西定律。
通过基本假定可将隧道化简为如图2所示水压力计算模型,公式的推导如下。
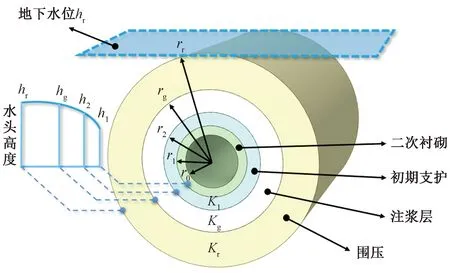
hr为地下水位;h1、h2、hg分别为水头高度;k为渗透系数;r为轴向半径图2 简化水压力计算模型Fig.2 Simplified water pressure calculation model
地下水的渗流连续性方程是质量守恒方程,它表明渗流场内任何一个“局部”均满足质量守恒定律。假设地下水和介质为刚体(不可压缩),基于微元法分析得出的三维渗流连续性方程为
(1)
式(1)中:vx、vy、vz分别为直角坐标系下流入微元体的地下水在3个方向上的流速。
考虑地下水满足达西定律及土体各项同性得
(2)
式(2)即为拉普拉斯方程,它表示各向同性土体的三维渗流微分方程。
将式(2)转化为柱坐标形式得
(3)
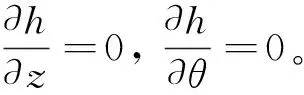
式(3)可以得到极大简化为
(4)
对式(4)积分可得
(5)
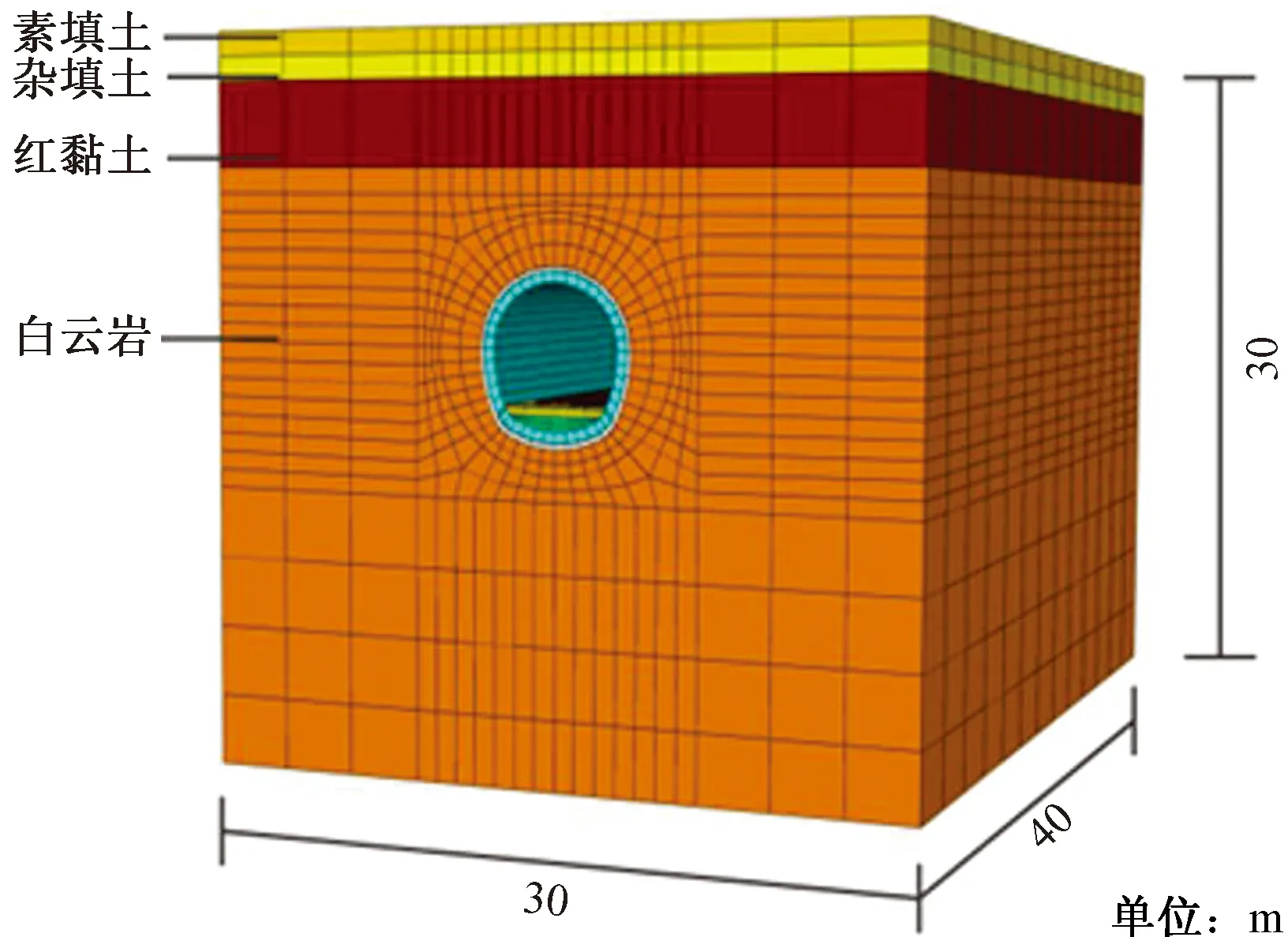
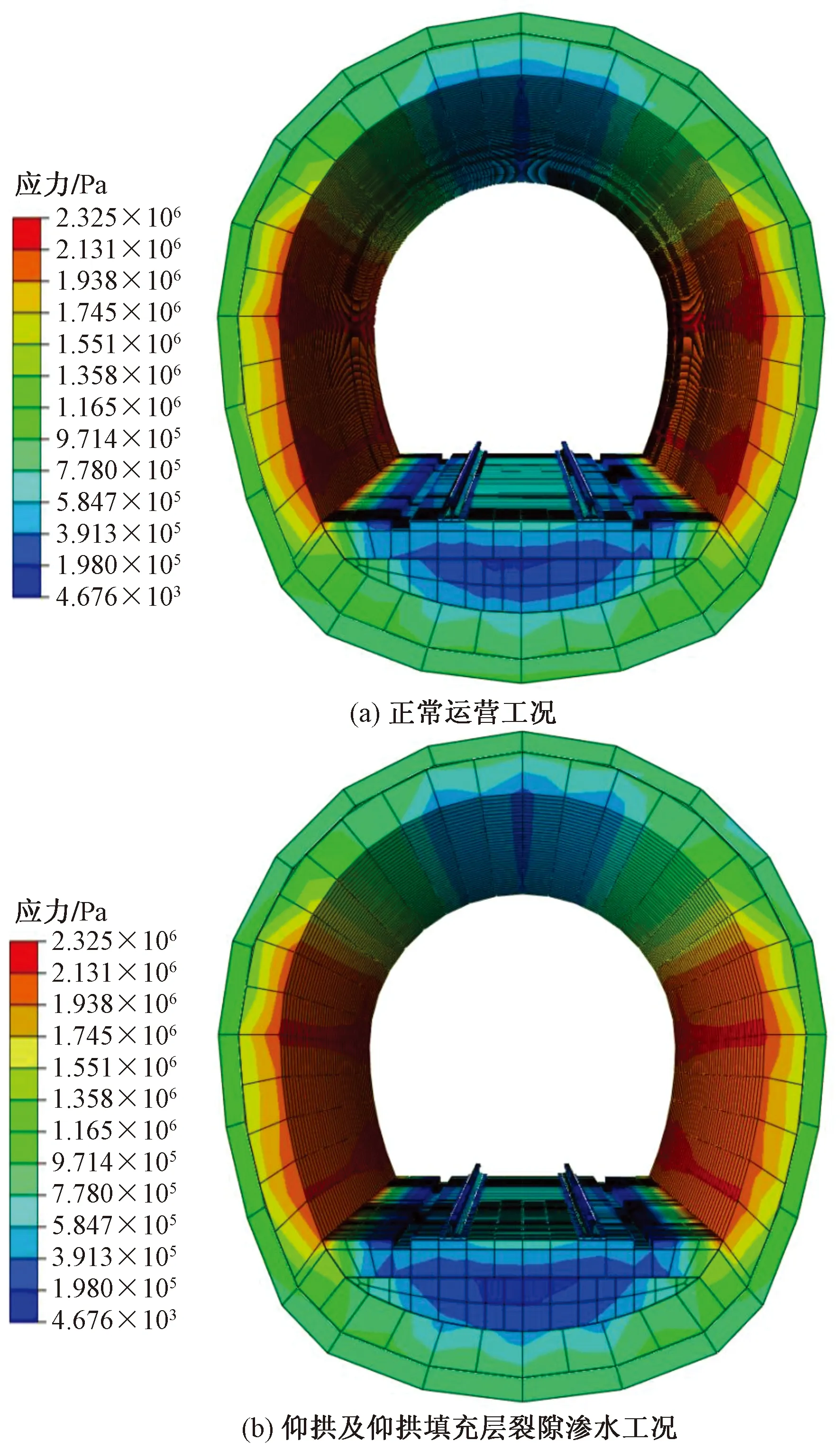
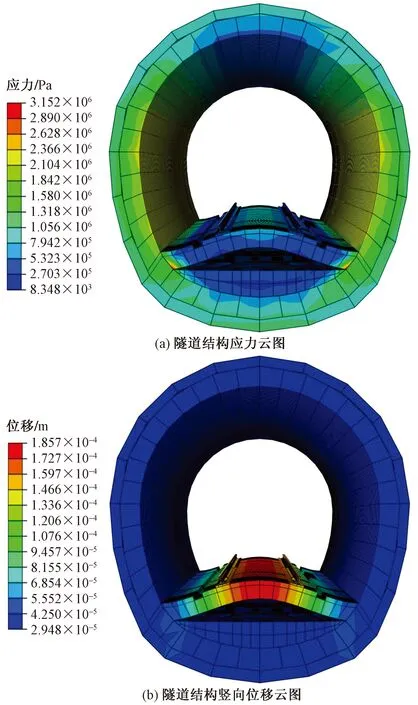
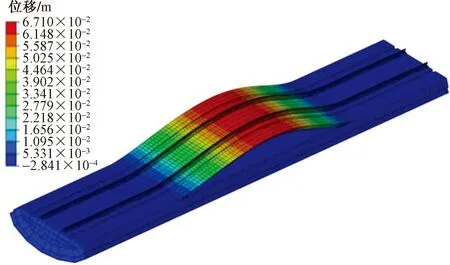
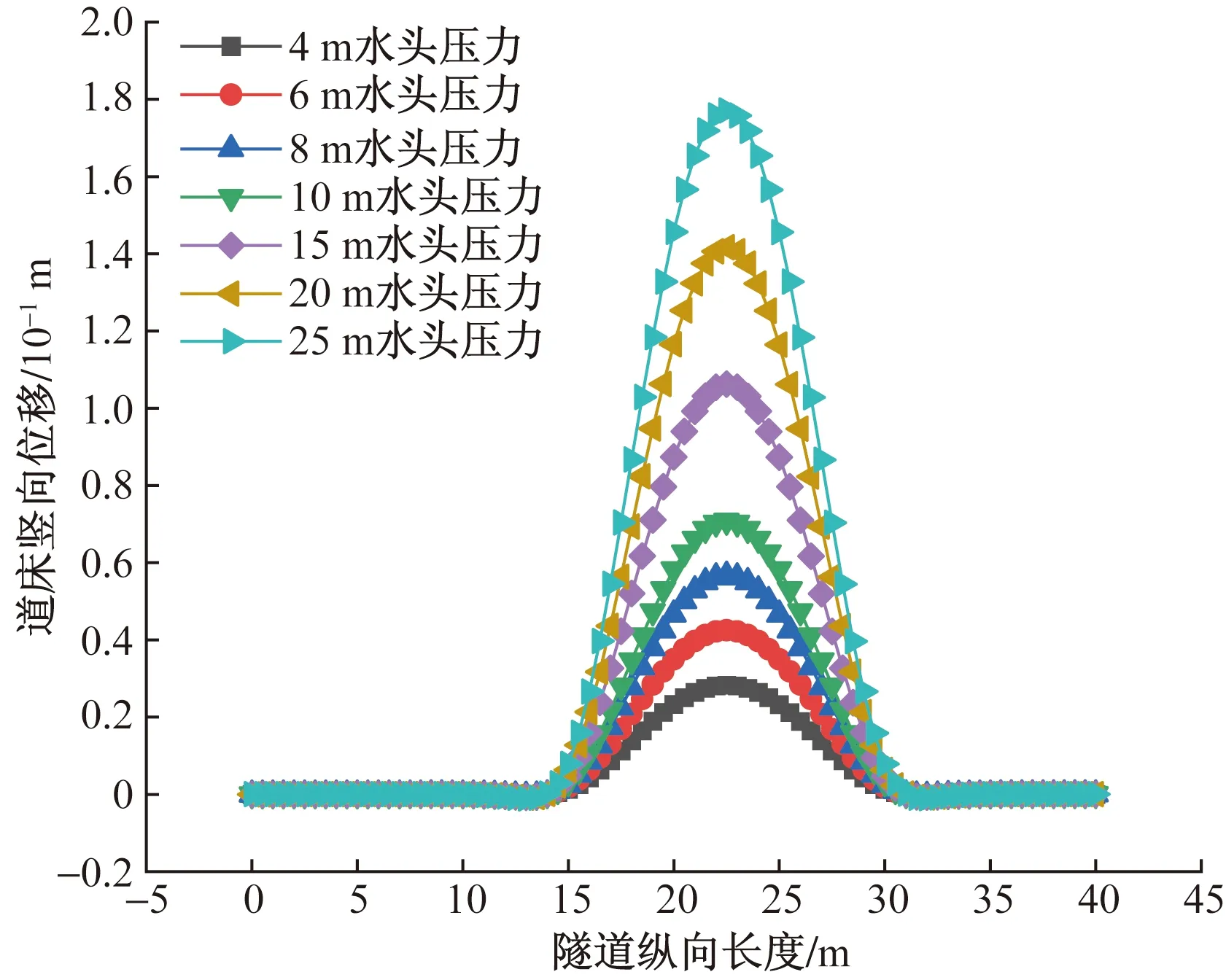
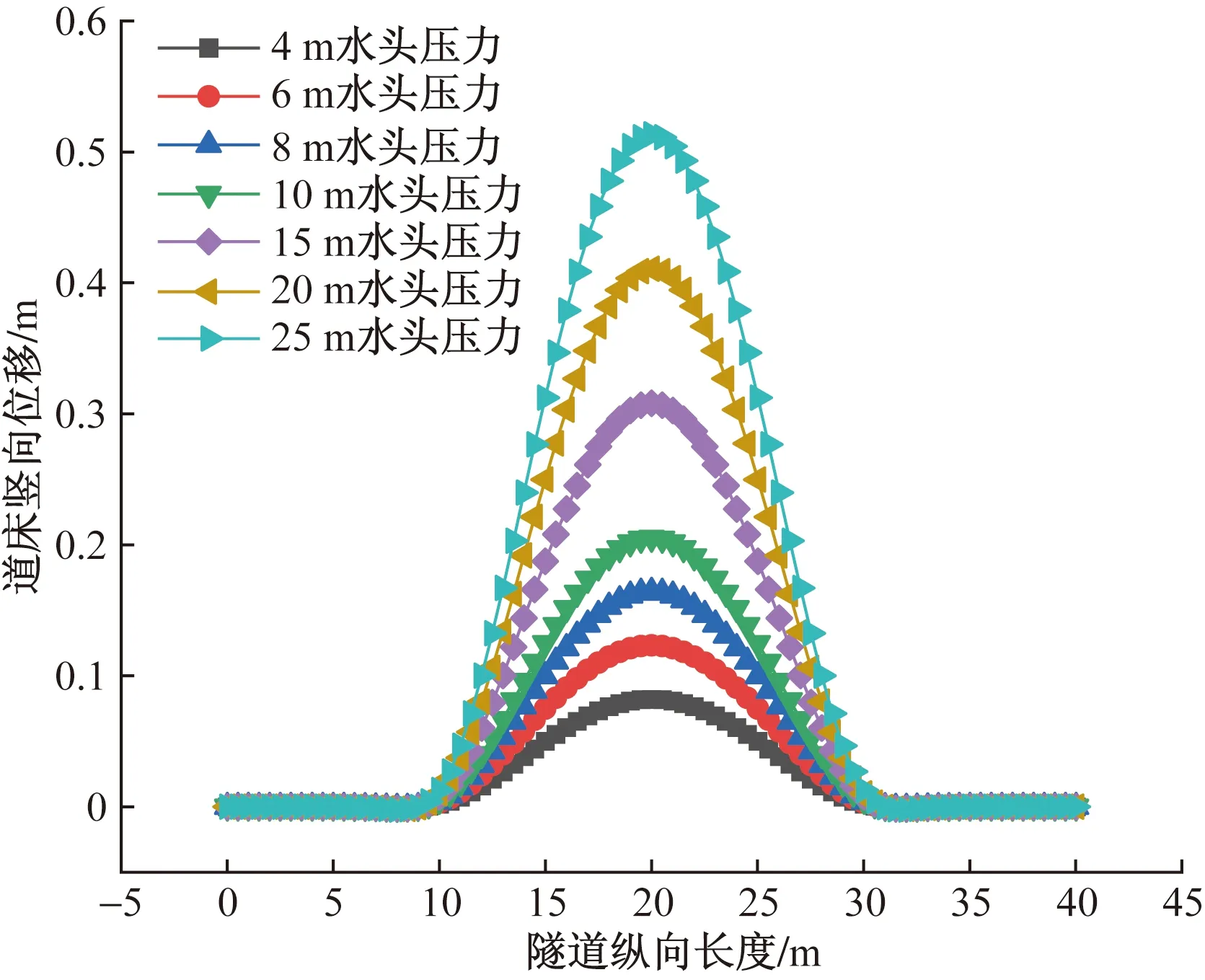
沿隧道纵向取1 m长度(单位长度),此时渗流长度即为r,当rr (6) (7) (8) 同理对于rg (9) (10) 因为Q1=Q2=Q3,联立方程组得 (11) 将h2解出得 (12) 则结构背水压力为 (13) 推导结构背水压力计算公式[式(13)]与高新强[20]提出深埋隧道限排情况下衬砌背后水压力公式相似。 根据典型工程案例的设计方案资料,采用ABAQUS有限元软件对单线隧道道床所处的正常运营、仰拱与仰拱填充层裂隙渗水、仰拱与仰拱填充层裂隙渗水且道床水平脱空、仰拱与仰拱填充层裂隙渗水且道床纵向脱空4种工况进行数值模拟。对比分析处于不同工况下随水压力上升以及脱空长度增加的道床上浮值,研究分析理论道床上浮曲线与数值模拟道床上浮曲线的差异,探究影响道床上浮值的关键因素,具体工况详见表1。 表1 数值试验工况Table 1 Numerical test conditions 数值计算模型上边界为地表,建立隧道-围岩三维数值计算模型,围岩竖向和横向取30 m,沿隧道纵向为40 m。隧道为深埋隧道,根据成拱效应计算的土压力,等效为上覆土层厚度9.3 m。孔隙水压力沿埋深变化加载对应深度围岩。等效覆土层厚度小于水压力高度时,在模型上表面加载高出部分水压力后沿围岩深度不断增加。地表为自由边界,其余5个面均约束法向变形,各部件接触采用绑定接触,模型共划分了38 666个六面体单元,数值计算模型如图3所示。 图3 整体数值模型Fig.3 Integral model 2.2.1 数值模型参数的选取 隧道结构模型中喷射混凝土、混凝土材料、轨道钢材采用线弹性模型;按照工程地质勘察资料,结合经验值选取,上覆地层参数采用莫尔-库伦模型,模型中材料的物理力学参数见表2。 表2 数值模型参数Table 2 Numerical model parameters 2.2.2 工况模拟方法 通过温度场变化改变仰拱与仰拱填充层的孔隙率,从而模拟仰拱与仰拱填充层裂隙渗水。 通过道床与仰拱填充层间接触面绑定约束的解除或取消,来模拟道床脱空。在道床脱空后,对脱空面施加对应埋深的水压力,模拟道床脱空后在水压力作用下发生上浮。 若隧道为浅埋隧道且为全包型防水,衬砌完全不透水,衬砌背后不设排水系统,则衬砌背后的水压力即为静水压力,不进行折减。 该工况的隧道仰拱底部处于20 m深的水压力环境中图3为案例工程正常运营工况与仰拱、仰拱填充层产生裂隙渗水工况的孔隙水压力、应力、竖向位移云图。可以看出,仰拱与仰拱填充层开始渗水后,仰拱与仰拱填充层的孔隙水压力开始降低,而道床孔隙水压力开始增高。图5中,在仰拱与仰拱填充层渗水后,道床应力减小,是因为地下水的浮力对道床自重应力产生了抵消。图6显示,整个隧道结构的正常运营工况在重力作用下产生了向下的位移。而当仰拱与仰拱填充层渗水后,由于仰拱底部孔隙水压力的减小,造成了隧道结构所受浮力减小,导致了渗水段隧道结构进一步的下沉,道床下沉总值最大为0.50 mm,如图7所示。如图8(a)所示,提取左、右轨道与隧道中线竖向位移。正常运营工况与渗水工况的道床下沉最大差值为0.04 mm,显示道床黏结性良好的情况下,仰拱与仰拱填充层渗水对道床上浮的影响可以忽略[图8(b)]。 图5 围岩-隧道三维模型孔隙水压力云图Fig.5 Nephogram of pore water pressure of surrounding rock tunnel three-dimensional model 图6 隧道结构应力云图Fig.6 Stress nephogram of tunnel structure 图8 无砟道床竖向位移曲线Fig.8 Vertical displacement curve of ballastless track bed 解除道床与仰拱填充层的绑定约束,横向两端仍绑定于衬砌,通过仰拱与仰拱填充裂隙作用于道床的地下水压力用等效压强代替。图9为道床在地下水深为20 m的环境中的应力、位移云图,可知:道床与衬砌接触部位应力值为1.85 MPa,出现应力集中现象;道床中部为道床最大上浮位置,上浮值为0.18 mm≤8.00 mm,不影响轨道交通正常运营。改变道床所处的不同水压力环境后,道床横向上浮曲线如图10所示,可以看到随水压力的增大,道床上浮值增量不足以影响轨道交通运行,道床处于25 m深的水压力环境中,最大上浮值也仅有0.22 mm。 图9 隧道结构云图Fig.9 Cloud diagram of tunnel structure 图10 道床横向上浮值Fig.10 Cloud diagram of tunnel structure 沿隧道纵向解除道床与仰拱填充层的绑定约束,通过仰拱与仰拱填充层裂隙作用于道床的地下水压力用等效压强代替,隧道基底受地下水水压影响,开展纵向道床脱空上浮工况,水压力及脱空示意图如图11所示。图12和图13为工程案例背景中道床处于地下水深为20 m的环境中,并产生20 m长纵向脱空上浮的应力、位移云图。可以看出,道床上浮分界部位产生了应力集中,应力值为40.81 MPa,在此应力状态下必定会造成混凝土道床的压碎与开裂,这与现场实际状况一致。道床沿纵向上浮,最大上浮值位于道床纵向中部,数值为6.71 cm,远大于正常运营的轨道交通道床上浮阈值8.00 mm。 图12 道床板脱空上浮应力云图Fig.12 Nephogram of floating stress of track bed slab 图13 道床板脱空上浮位移云图Fig.13 Nephogram of track bed slab floating displacement 分别取脱空道床纵向长度为5、10、15、20 m,使脱空道床处于逐渐增高的水压力环境下,提取道床中线的竖向位移曲线。如图14所示,当道床脱空上浮段为5 m时,道床在4~25 m深的水压力环境下,均不会产生影响轨道交通运营的上浮值,道床在25 m深的水压力环境中,最大上浮值也仅有0.78 mm,远小于正常运营的轨道交通道床上浮阈值8.00 mm,但当道床在20 m深的水压力环境中,模拟上浮曲线峰值0.62 mm。 如图15所示,当道床脱空上浮段增大至10 m时,道床在4~25 m深的水压力环境下,在隧道道床上浮值允许范围内,在25 m深的水压力环境中,道床最大上浮值为6.83 mm,逐渐向正常运营的轨道交通道床上浮阈值8.00 mm接近,道床在20 m深的水压力环境中,上浮曲线峰值5.47 mm。 图15 10 m道床脱空上浮值Fig.15 Free floating value of 10 m track bed 如图16所示,当道床脱空上浮段长度增加至15 m时,处于8 m以上深的水压力环境中,便会产生影响轨道交通正常运营的道床上浮值,当道床在20 m深的水压力环境中,模型计算道床上浮曲线峰值2.31 cm。 图16 15 m道床脱空上浮值Fig.16 Free floating value of 15 m track bed 如图17所示,当道床脱空上浮段长度增加至20 m时,道床仅在4 m深的水压力环境中,道床也会产生超过阈值8 mm的上浮,且在20 m深的水压力环境下,道床上浮模拟曲线峰值6.71 cm,随着道床承受水压力增大,道床上浮模拟值发展趋势较快。 图17 20 m道床脱空上浮值Fig.17 Free floating value of 20 m track bed 建议隧道道床上浮预防措施:一方面应加强隧道防水,控制仰拱与仰拱填充层质量,消除隧道渗水;另一方面可以采取仰拱底部或道床底部的降压排水措施,减小结构所受水压力。再有道床浇筑前重视浇筑面(仰拱填充面)的凿毛、清洗,必要时预埋植筋或锚杆,做好新老混凝土的连接,保证黏结强度,是防止道床上浮的有效措施。 通过前述的分析可知:在道床与仰拱填充层黏结良好的情况下,渗水段隧道会在孔隙水压力的减小下,发生不影响隧道运营安全的下沉。当一定大小的孔隙水压力作用于脱空段道床后,道床开始与仰拱填充层分离并发生上浮。 其中,道床若仅发生横断面上的脱空上浮,由于道床脱空上浮段落较小,并不会产生影响轨道交通运营的上浮值,但在纵向发生道床上浮,随着道床脱空上浮段长度的增加,会产生远大于道床上浮阈值8.00 mm的上浮值,并且相较于水压力增大引起的道床上浮值增大,道床脱空上浮段长度的增加对道床上浮影响更加明显,可见,相较于地下水压力大小的难以控制,以及隧道净空固定与材料造价对道床抗弯刚度的限制,减小道床脱空上浮段的长度能有效减小道床上浮值。 围绕轨道交通隧道道床上浮底鼓问题,建立基于岩溶隧道道床上浮机理的底鼓力学计算模型,采用理论分析与ABAQUS数值计算结合方法,讨论隧道道床上浮机制及抑制措施。结果如下。 (1)采用数值计算方法得到隧道道床横向脱空与纵向脱空两大类的上浮影响曲线,可划分三种阶段,包括:第一阶段地下水入渗阶段;第二阶段黏结失效阶段;第三阶段道床局部上浮脱空阶段。 (2)第一阶段中仰拱填充层粘接良好的无砟道床工况下,得到6 MPa的隧道水压力,可以发生道床脱空上浮。表明隧道无砟道床脱空上浮主要是由仰拱填充层-道床的新老混凝土接触面黏结力较弱或失效造成。 (3)研究临界水头高度与道床板厚度、道床与仰拱填充间黏结强度之间的关系,得出由于道床横截面长度较短,发生局部脱空后,在水压力作用下上浮值较小,但当道床纵向截面发生整体脱空,将引起较大的道床上浮位移。道床脱空上浮长度是控制无砟道床上浮值的主要参数。 (4)通过计算分析得到道床上浮临界水头高度,当道床上浮值超越黏结强度阈值后,隧道道床上浮底鼓,利用道床上浮计算峰值公式带入上浮阈值8.00 mm,反算补打锚杆纵向间距,补打道床锚杆,增强道床与仰拱填充层的黏结强度,可有效治理道床上浮。同时,道床应急钻孔、切割边沟泄水,将涌水导入道床边沟排出,控制上浮道床标高降低趋于稳定。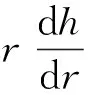
2 数值仿真模型
2.1 数值试验工况与参数

2.2 数值模型建立与参数

3 计算结果与分析
3.1 道床黏结状态下的位移情况


3.2 道床横向中部脱空的位移情况

3.3 道床纵向局部脱空的位移情况


4 结论

