基于K近邻算法的钢筋混凝土柱地震破坏模式判别方法
杨程, 颜海泉, 董正方*
(1.河南大学土木建筑学院, 开封 475004; 2.上海市政工程设计研究总院(集团)有限公司, 上海 230031)
钢筋混凝土(reinforced concrete,RC)柱作为工程中常见的承重结构[1],在建筑结构工程中发挥着重要的作用,受到地震作用会呈现三种不同的破坏模式(弯曲破坏、弯剪破坏、剪切破坏),对工程结构造成重大影响[2]。不同的破坏模式会导致RC柱地震损伤特征具有差异性[3]。所以,通过寻找参数与破坏模式之间的规律,并建立一种合适的地震破坏模式判别方法,更有利于钢筋混凝土结构抗震性能评价和加固的开展。
目前,RC柱的地震破坏模式判别方法大致可以分为传统经验法和机器学习法二大类。传统经验法主要对实验数据归纳与分析,将某一个参数或者多个参数与地震破坏模式联系起来。例如,文献[4-5]分别基于单一的抗剪需求与抗剪承载力之比或者剪跨比给出了RC柱不同地震破坏模式的判别区间;文献[6]则以轴压比、剪跨比、箍筋参数、纵筋参数4个参数以概率方法提出一种综合判断指标判别法,并给出了判别表达式。经验法的特点是使用方便,但判断结果可靠性较低[7]。
近几年机器学习在土木工程方向发展较为迅速[8],与传统经验法方法相比,其优点是可以通过探索参数与3种地震破坏模式之间存在的某种内在联系。例如,文献[9]对比了6种不同机器学习算法对地震破坏模式判别精度;文献[10]基于朴素贝叶斯分类算法建立了RC柱地震破坏模式的判别方法;文献[11]建立了随机森林算法与RC柱地震破坏模式之间的关系。上述机器学习方法在一定程度上比传统经验法准确率要高,但是仍存在以下不足:一是数据集样本不均衡时,导致机器学习算法对少数类破坏模式判别精度较低[12];二是没有筛选出最佳参数,所建立的模型常常将所有的参数作为模型输入指标,会导致使用判别模型时较复杂。例如,文献[9]在使用K-近邻(K-nearest neighbor,KNN)方法建立模型时没有进行参数的筛选,导致计算模型复杂,判别准确率较低。因此,需要均衡少数类样本数据集,筛选出使RC柱地震破坏模式判别模型准确率达到最佳的参数,并建立相应的地震破坏模式判别模型。
现首先基于合成少数过采样技术(synthetic minority over-sampling technique,SMOTE)算法生成初始均衡数据,接着依据编辑近邻(edited nearest neighbours,ENN)算法分别筛选出判别弯曲破坏和非弯曲破坏、弯剪破坏和剪切破坏的最佳参数;通过TomekLinks算法合理剔除噪音样本,然后根据筛选的最佳参数并结合KNN算法[13],建立两阶段KNN模型,达到准确判别RC柱破坏模式的目的。通过与传统KNN模型以及3种传统经验法做对比,验证模型所提模型的优异性。
1 处理不平均衡数据的算法
SMOTE算法主要是利用将少数类样本通过人工合成新的样本来对其进行扩充,从而使整个样本达到均衡。RC柱破坏模式不平衡数据问题可以描述为
Tm+n={Am,Bn}
(1)
Am={Ai|i=1,2,…,m}
(2)
Bn={Bi|i=1,2,…,n}
(3)
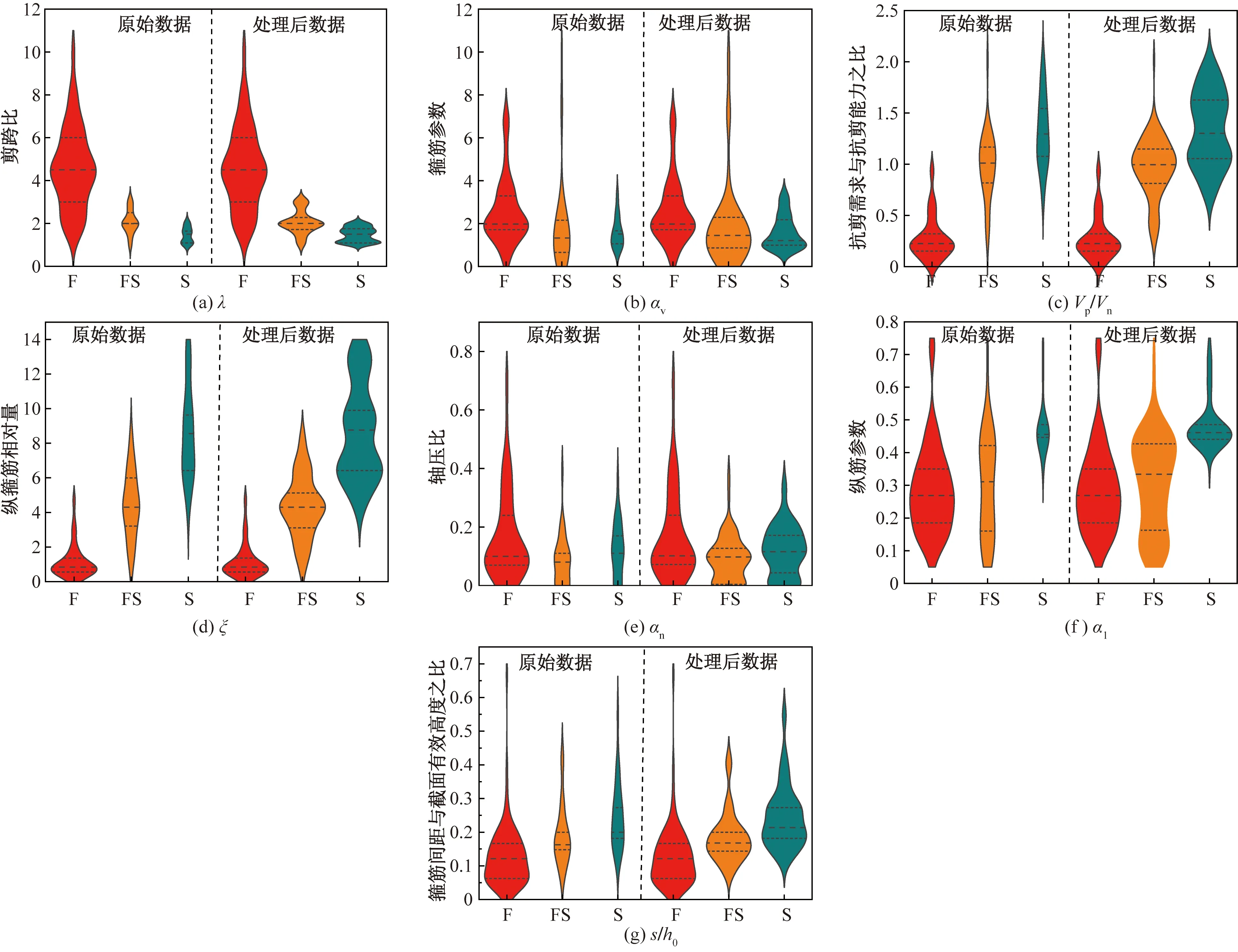
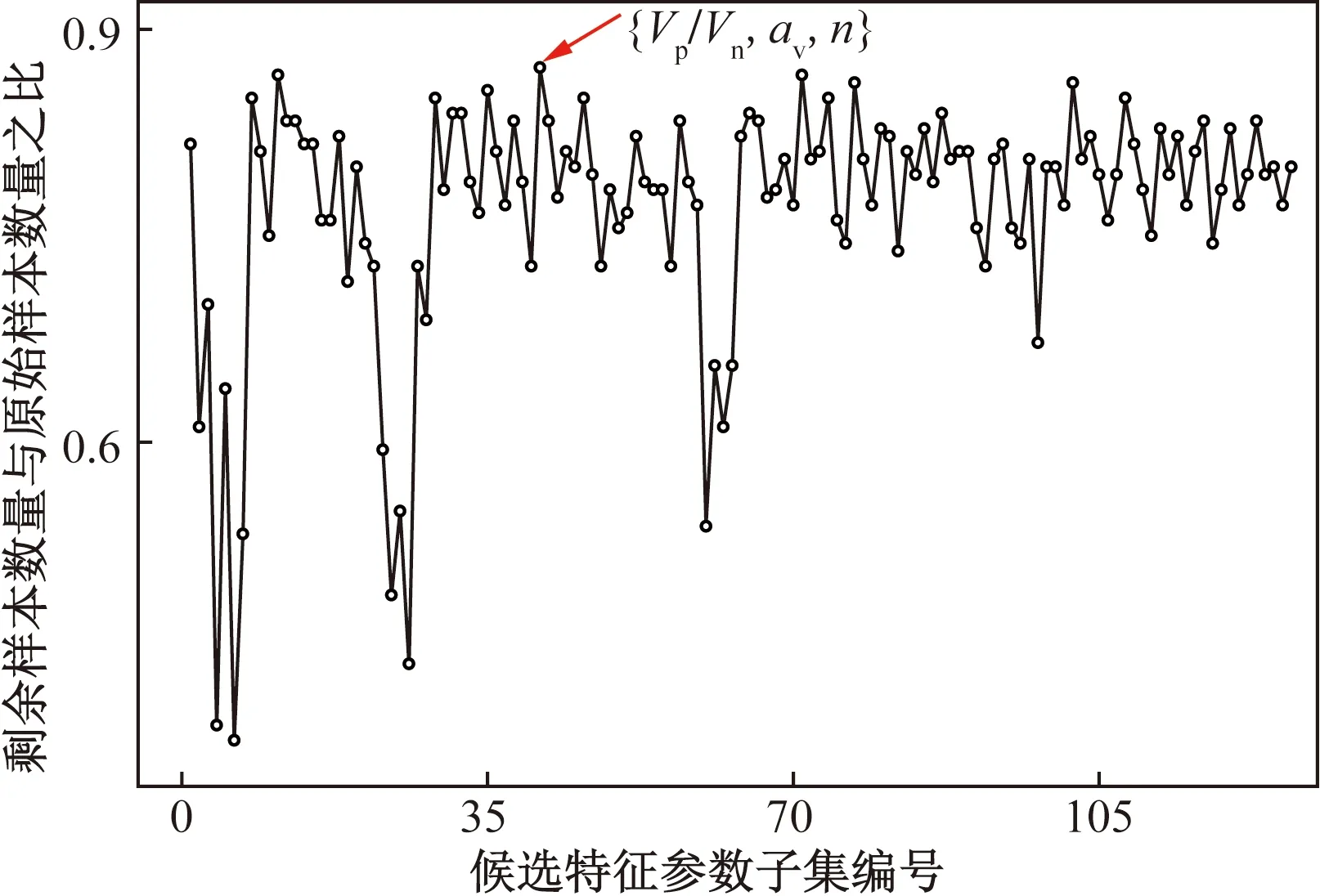
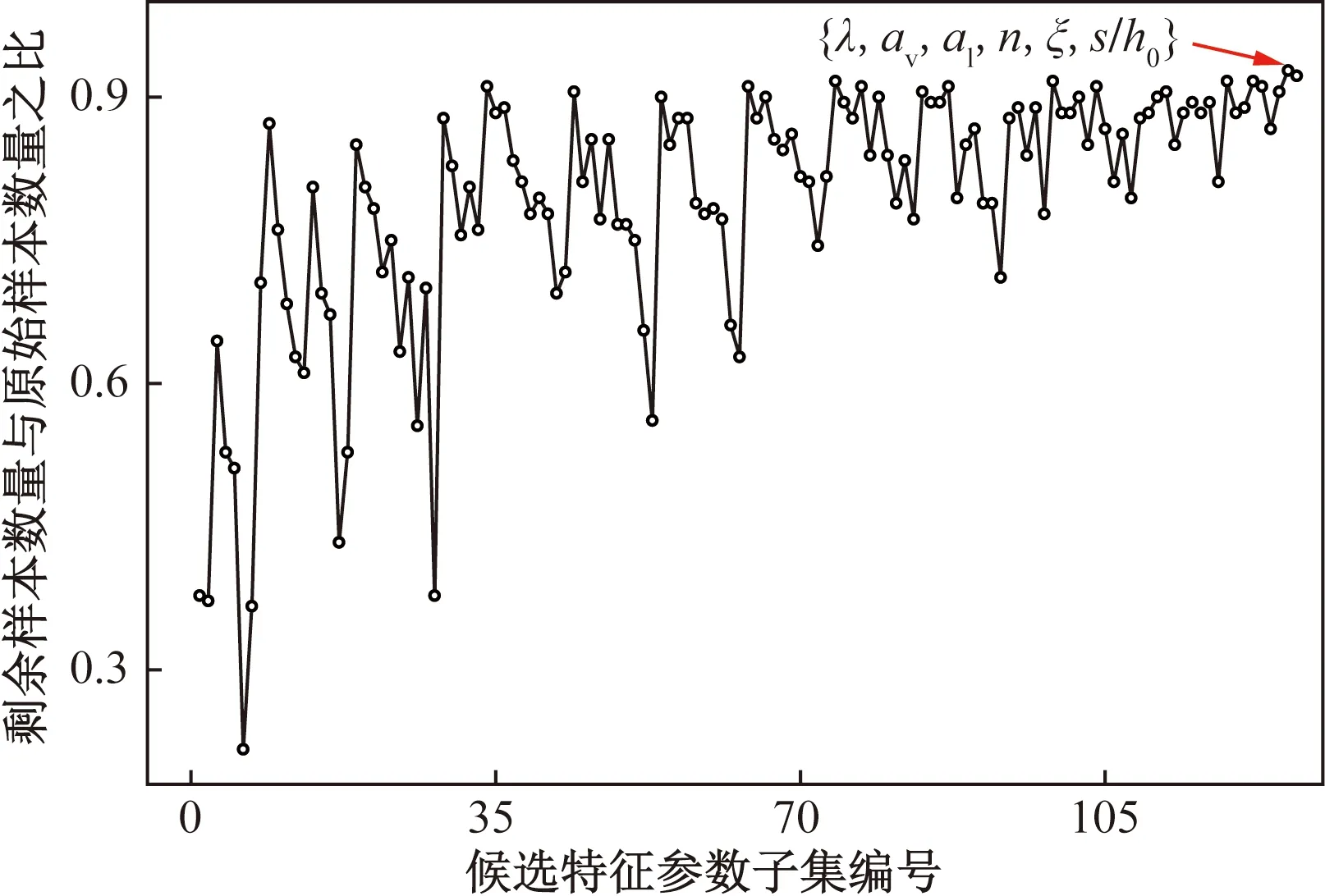
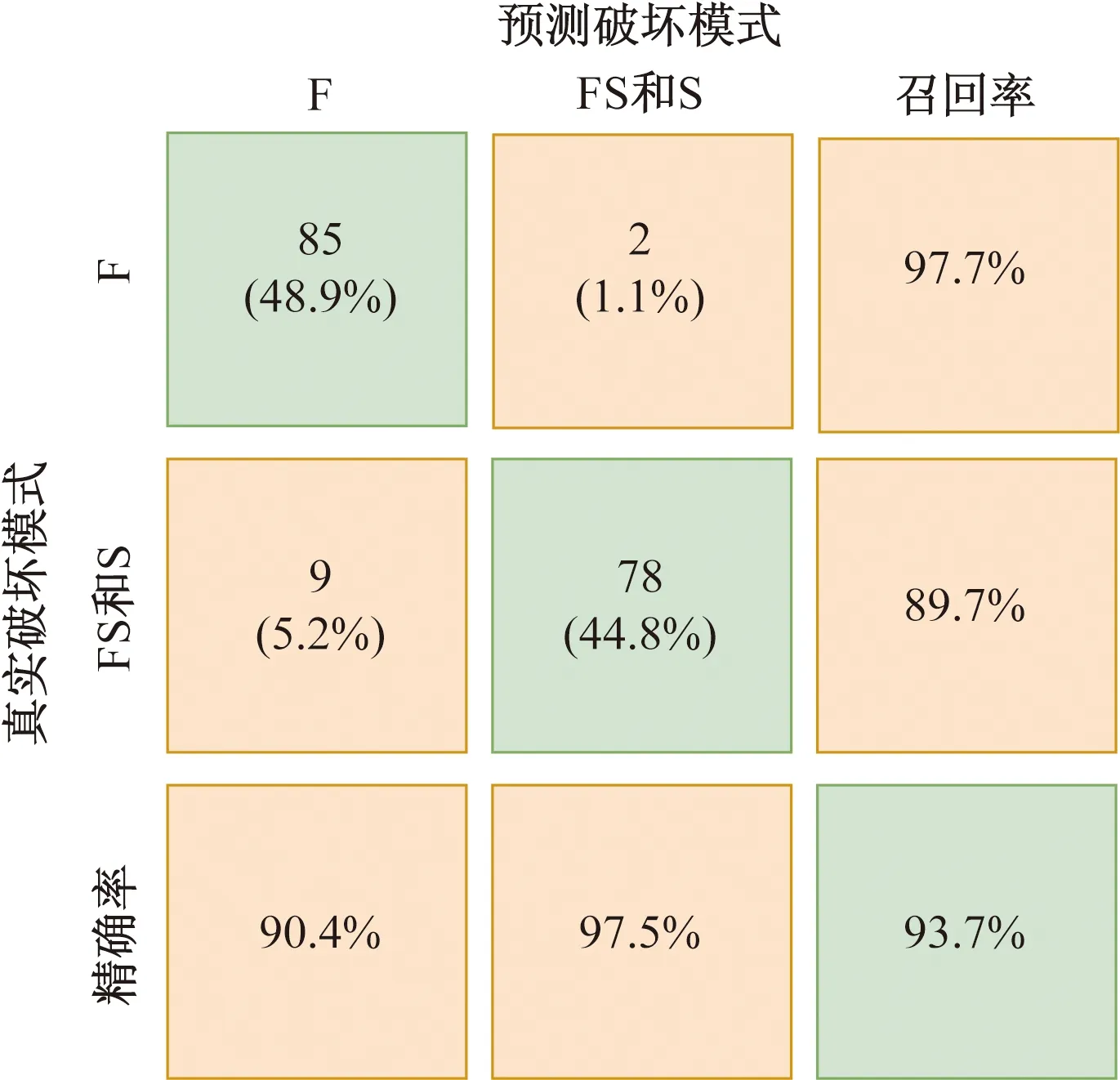
式中:Tm+n为不平衡数据集;Am为少数类破坏模式的数据集(如剪切破坏或弯剪破坏);Bn为多数类破坏模式数据集(如弯曲破坏);Ai和Bi分别为少数类样本和多数类样本的第i个样本点;m和n分别为少数类和多数类破坏模式数据集的样本个数,且m 如图1所示,根据SMOTE算法[14]选定与Ai距离最近的ki个同类样本点Aik(k=1,2,…,ki),在样本点Ai与Aik之间可以合成新样本点A′ik,表达式为 图1 基于SMOTE算法的过采样过程Fig.1 Oversampling process based on SMOTE A′ik=Ai+η(Aik-Ai) (4) 式(4)中:η为(0,1)的随机数。对于少数类样本数据集Am中的每个样本Ai(i=1,2,…,m),可以根据式(4)随机合成ki个新样本点。所以使用SMOTE算法进行采样,可以将少数类样本个数由m个调整到n个,进而达到初始平衡数据。 不同参数对RC柱的地震破坏模式影响程度不尽相同,目前较为常用的有抗剪需求与抗剪承载力之比(Vp/Vn)[4]、剪跨比(a/h0)[5]、纵箍筋相对量(ξ=∑Aslfy/∑Asvfyv)[15]、纵筋参数(αl=ρlfy/f′c)、箍筋参数(αv=ρvfyv/ft)、轴压比(n)[6]、箍筋间距与截面有效高度比(s/h0)[16]等。其中a为剪跨,h0为截面有效高度,∑Asl为柱子截面的单侧受拉纵筋的面积,∑Asv为柱高范围内所有箍筋的截面面积之和,fyv为箍筋的屈服强度,fy为纵筋的屈服强度,ρl为配筋率,f′c为混凝土抗压强度,ρv为配箍率,ft为混凝土抗拉强度,s为箍筋间距。为了探究上述7个参数与RC柱地震破坏模式之间的关系,从PEER数据库[17]中收集了148组(弯曲破坏90组、弯剪破坏33组和剪切破坏25组)圆形截面RC柱的破坏试验数据。 为了验证SMOTE算法生成数据集的合理性,得到不同地震破坏模式下各参数的小提琴图如图2所示。其中。分析图2可知,SMOTE算法生成数据不会改变原始数据集数据分布特点,说明SMOTE算法生成数据具有一定合理性;另外从图2中可以看出,参数Vp/Vn、s/h0、ξ和αl越大,或者αv和a/h0越小,RC柱的越容易发生剪切破坏;反之RC柱越容易发生弯曲破坏;参数n对3种破坏模式并没有特别大的影响。 F为弯曲破坏RC柱,FS为弯剪破坏RC柱,S为剪切破坏RC柱;小提琴外部形状为核密度估计图;每个小提琴图中的虚线从下到上分别为该样本中所有数值由小到大排列后第25%、50%、75%的数字图2 各参数在不同地震破坏模式下的小提琴图Fig.2 Violin diagram of characteristic parameters for different earthquake failure modes 为了进一步分析参数对RC柱地震破坏模式的影响,得到各参数不同破坏模式之间数据均值的增长率或减少率(以剪跨比为例,弯曲破坏均值为4.56、弯剪破坏均值 2.01、剪切破坏均值为1.33,则弯曲破坏到弯剪破坏的减少率为56%、弯剪破坏到剪切破坏的减少率为34%)如表1所示。 表1 各参数不同破坏模式之间增长率或减少率Table 1 Change rate of different failure modes of different parameters 由表1可知,通过观察各种参数的之间的变化率,可以看出不同特征之间变化率差异比较明显,所以需要考虑不同参数对地震破坏模式的影响;通过观察同一参数不同破坏模式之间变化率,可以看出变化率也比较大,所以有必要将破坏模式进行分开研究,分别研究不同破坏模式之间参数对其影响。 综合以上分析研究,首先分别筛选出第一阶段和第二阶段RC柱地震破坏模式的最佳参数,根据最佳参数分别建立不同阶段的判别模型,具体判别流程如下:第一阶段判别RC柱是发生弯曲破坏还是非弯曲破坏,根据第一阶段的结果判断是否进行第二阶段,第二阶段需要针对非弯曲破坏进一步判断,判别RC柱是发生弯剪破坏还是剪切破坏。 ENN[18]算法是对数据集每一个样本采用KNN模型检测,若检测结果与实际类别标签相悖,则认为该样本为噪声样本,并剔除相应样本。最终是基于KNN算法做判别模型,针对上述7个参数总计127(即27-1)参数组合情况,对于每一种组合情况采用ENN进行去噪,通过剩余样本数量与原始样本数量的比值大小来确定最佳组合,考虑到ENN算法去噪原理是基于KNN算法,剩余样本数量与原始样本数量比值越大就说明该组合选取越合理,这样使KNN算法做判别模型的效果达到最好。上述7个参数都是无量纲的,因此可以排除量纲对本文模型的影响。但是通过上述小提琴图可以看出不同的参数的取值范围有着较大差异,这样会导致取值范围较大的参数会比取值范围较小的参数在模型训练中提供更多的信息,导致对判别的结果有影响。因此,为了消除此影响,对每个参数的取值范围做了规定,即 (5) 式(5)中:A为原始参数;Amin为原始参数中的最小值;Amax为原始参数中最大值;A′为处理后的数据。 为筛选第一阶段模型(用来判别弯曲破坏和非弯曲破坏)的最佳参数,根据前述7个参数组成的原始参数集{Vp/Vn,s/h0,a/h0,αl,ξ,n,αv}生成127(27-1)个参数候选子集;根据180组试验数据(弯曲破坏和非弯曲破坏都为90组),通过ENN算法,得到结果如图3所示。当候选参数子集编号k为41时(此时参数子集为{Vp/Vn,αv,n}),剩余样本数量与初始样本数据比值达到最高;随着k不断增大,比值并不会有较大的变化,甚至还会有降低的趋势;所以第一阶段kNN模型最佳参数子集为{Vp/Vn,αv,n}。 图3 第一阶段最佳参数的筛选Fig.3 The selection of optimal characteristic parameters in the first stage 同理,为了筛选出第二阶段模型(用来判别弯剪破坏和剪切破坏)的最佳参数,采用由前述7个参数组成的原始参数集{Vp/Vn,s/h0,a/h0,αl,ξ,n,αv}生成的127个参数候选子集;基于180组试验数据(弯剪破坏和剪切破坏都为90组),通过ENN算法,其结果如图4所示。随着k的增加,剩余样本数量与初始样本数量的比值整体呈增大趋势,当候选参数子集编号k为126时(此时参数子集为{λ,αl,αv,n,ξ,s/h0}),剩余样本数量与初始样本数据比值达到最高。所以,第二阶段KNN模型最佳参数子集为{λ,αl,αv,n,ξ,s/h0}。 图4 第二阶段最佳参数筛选Fig.4 Optimal feature parameter selection in the second stage 综上所述,对于弯曲破坏和非弯曲破坏,可以通过{Vp/Vn,αv,n}3个参数来建立判别模型,对于弯剪破坏和剪切破坏可以通过{λ,αl,αv,n,ξ,s/h0} 6个参数来建立判别模型。通过上述参数筛选,对于弯曲破坏与非弯曲破坏(弯剪破坏与剪切破坏)从原始的7个参数简化到3个参数,对于弯剪破坏与剪切破坏从原始7个参数简化到6个参数,一定程度上简化了判别模型。 基于SMOTE算法进行过采样合成少数类样本数据集的过程中会有随机性,会产生噪声数据样本点,干扰分类器的分类性能,导致判别精度下降。TomekLinks[19]算法是一种欠采样算法;TomekLinks算法会剔除每对 TomekLink(如果A和B分别来自两个不同类别的样本且A和B互为最近,A和B就为一对TomekLink)中的多数类样本,假如两个样本个数一样多,则会剔除这一对。 当建立第一阶段模型(判别弯曲破坏和非弯曲破坏) 时,对174组(经过TomekLinks算法剔除噪声样本后,其中弯曲破坏和非弯曲破坏都为87组)RC柱地震破坏模式样本数据基于KNN算法进行分类,通过10折交叉验证得到判别RC柱地震破坏模式的第一阶段KNN模型的混淆矩阵如图5所示。 F为弯曲破坏RC柱,FS为弯剪破坏RC柱,S为剪切破坏RC柱;精确率表示预测样本中真实样本所占的比例,召回率表示真实样本被预测正确比例;混淆矩阵对角线上的绿色格上数值代表正确判别个数,带括号的百分数为正确样本个数占总样本的百分比,不带括号的百分数为样本的总体判别准确率;橙色格上的数值代表错误判别的个数,带括号的百分数为错误样本个数占总样本的百分比,不带括号的百分数分别代表各自破坏模式的精确率和召回率图5 第一阶段KNN模型Fig.5 The first stage KNN method 对于第一阶段KNN模型,弯曲破坏样本有2个样本被误判为非弯曲破坏,非弯曲破坏样本有9个样本被误判为弯曲破坏,模型整体准确率为93.7%。由此可见,第一阶段KNN模型的判别准确率相对较高。 当建立第二模型(判别弯剪破坏和剪切破坏)时,对180组(经过TomekLinks算法剔除噪声样本后,其中弯剪破坏和剪切破坏都为90组)RC柱地震破坏模式样本数据基于KNN算法进行分类,通过10折交叉验证得到最终结果。其结果如图6所示。图6中,对于第二阶段KNN模型,弯剪破坏样本有12个样本被误判为剪切破坏,剪切破坏样本有1个样本被误判为弯剪破坏,模型整体准确率为92.8%。由此可见,第二阶段KNN模型的判别准确率相对较高。 图6 第二阶段KNN模型Fig.6 The second stage KNN method 为了验证本模型的最终准确率,将实验的267组数据(弯曲破坏87组,弯剪破坏90组,剪切破坏90组)用上述两阶段模型进行判别,得到判别结果的混淆矩阵如图7所示。 图7 两阶段KNN模型最终结果Fig.7 Final result of two-stage KNN model 由图7可知,两阶段KNN模型对3种破坏模式(弯曲破坏、弯剪破坏、剪切破坏)召回率和精确率都较高,分别为98.9%、91.1%、98.9%和92.5%、97.6%、98.9%,整体准确率是96.3%,由此说明本文模型的误判率较低,对于3种破坏模式判错率都低于10%。 本文模型可以通过输入钢筋混凝土柱设计参数进行判断,第一阶段需要通过输入{Vp/Vn,αv,n} 3个参数来进行判别,判别RC柱的破坏模式是否是弯曲破坏,假如是弯曲破坏则不需要进行第二阶段判别,假如不是弯曲破坏则需要进行第二阶段判别,第二阶段通过输入{λ,αl,αv,n,ξ,s/h0} 6个参数来判别RC柱发生弯剪破坏还是剪切破坏。 为了验证两阶段KNN模型准确率的优异性,将该方法与传统KNN模型、3种传统经验法[4-6](表2)判别性能进行对比分析。用148组RC柱破坏模式实验样本(F:90组、FS:33组、S:25组)去验证传统KNN模型以及3种传统经验法(分别记为模型1、模型2、模型3)的准确率,得到的判别结果如图8所示。 表2 传统经验法RC柱破坏模式判别方法Table 2 Traditional empirical method to distinguish failure mode of RC column 由图8(a)可知,传统KNN模型对弯曲破坏、弯剪破坏、剪切破坏判别错误个数分别为5、12、4,召回率分别为94.4%、63.6%、84.0%,精确率分别为92.4%、70.0%、80.7%,模型整体的准确率为85.5%,可见传统KNN模型对于弯曲破坏和剪切破坏判别准确率较高,对于弯剪破坏判别准确率较低;由图8(b)可知,模型1对弯曲破坏、弯剪破坏、剪切破坏判别错误个数分别为12、20、4,召回率分别为86.7%、39.3%、84.0%,精确率分别为92.9%、46.4%、58.3%,模型1整体的准确率为75.7%,可见模型1对于弯曲破坏和剪切破坏判别准确率较高,对于弯剪破坏判别准确率较低;由图8(c)可知,模型2型对弯曲破坏、弯剪破坏、剪切破坏判别错误个数分别为27、18、5,召回率分别为70.0%、45.5%、80.0%,精确率分别为100%、41.7%、40.8%,模型2整体的准确率为62.2%,可见模型2模型对于弯曲破坏和剪切破坏判别准确率较高,对于弯剪破坏判别准确率较低;由图8(d)可以看出,模型3对弯曲破坏、弯剪破坏、剪切破坏判别错误个数分别为0、30、10,召回率分别为100%、9.1%、60%,精确率分别为81.8%、37.5%、50%,模型3整体的准确率为73.0%,可见模型3对于弯曲破坏和剪切破坏判别准确率较高,对于弯剪破坏判别准确率较低。说明传统KNN模型、模型1、模型2、模型3这4种方法对于弯曲破坏样本和剪切破坏样本一定程度上能够准确判别,但是弯剪破坏样本被误判较多。所以上述4种模型虽然一定程度上能够对弯曲破坏样本和剪切破坏样本进行正确判断,但是对于弯剪破坏样本判别准确率较低,不能够兼容整体上的准确率。 综合以上分析,传统的KNN模型、基于抗剪需求与抗剪承载力之比判别模型、基于剪跨比判别模型、多参数判别模型不能够同时保证3种破坏模式有着较高的准确率,有较多弯剪破坏样本被误判,从而使弯剪破坏精确率和召回率较低,而本文模型不仅能够很大程度上提升弯剪破坏模式准确率,对于弯曲破坏模式和剪切破坏模式也有一定程度的提升,而且3种破坏模式的精确率和高召回率都可达90%以上。 通过处理不平衡数据、筛选最佳参数、剔除噪声样本等手段对KNN模型改进,并进行了方法之间的对比,得到下列结论。 (1)通过SMOTE算法生成的平衡数据,并根据ENN算法,筛选出了第一阶段和第二阶段KNN模型的最佳参数,分别为{Vp/Vn,αv,n}、{Vp/Vn,s/h0,a/h0,αl,ξ,n,αv}。 (2)通过引入TomekLinks算法,来寻找样本中的TomekLink对,可以有效剔除在初始平衡数据集生成阶段产生的噪声数据,从而获得高质量的平衡数据。 (3)两阶段KNN模型对于RC柱的3种破坏模式召回率和精确率以及整体准确率均可达到90%以上,比传统KNN模型整体判别准确率大约高10%,比基于抗剪需求与抗剪承载力之比判别模型整体准确率和多参数判别模型整体准确率高20%左右,比基于剪跨比判别模型整体准确率高34%。 本文方法不仅适用于RC柱的破坏模式判别,也可以用于其他钢筋混凝土构件破坏模式的判别以及其他同类型的问题;另外随着样本数量增加,本文模型精度会进一步提高。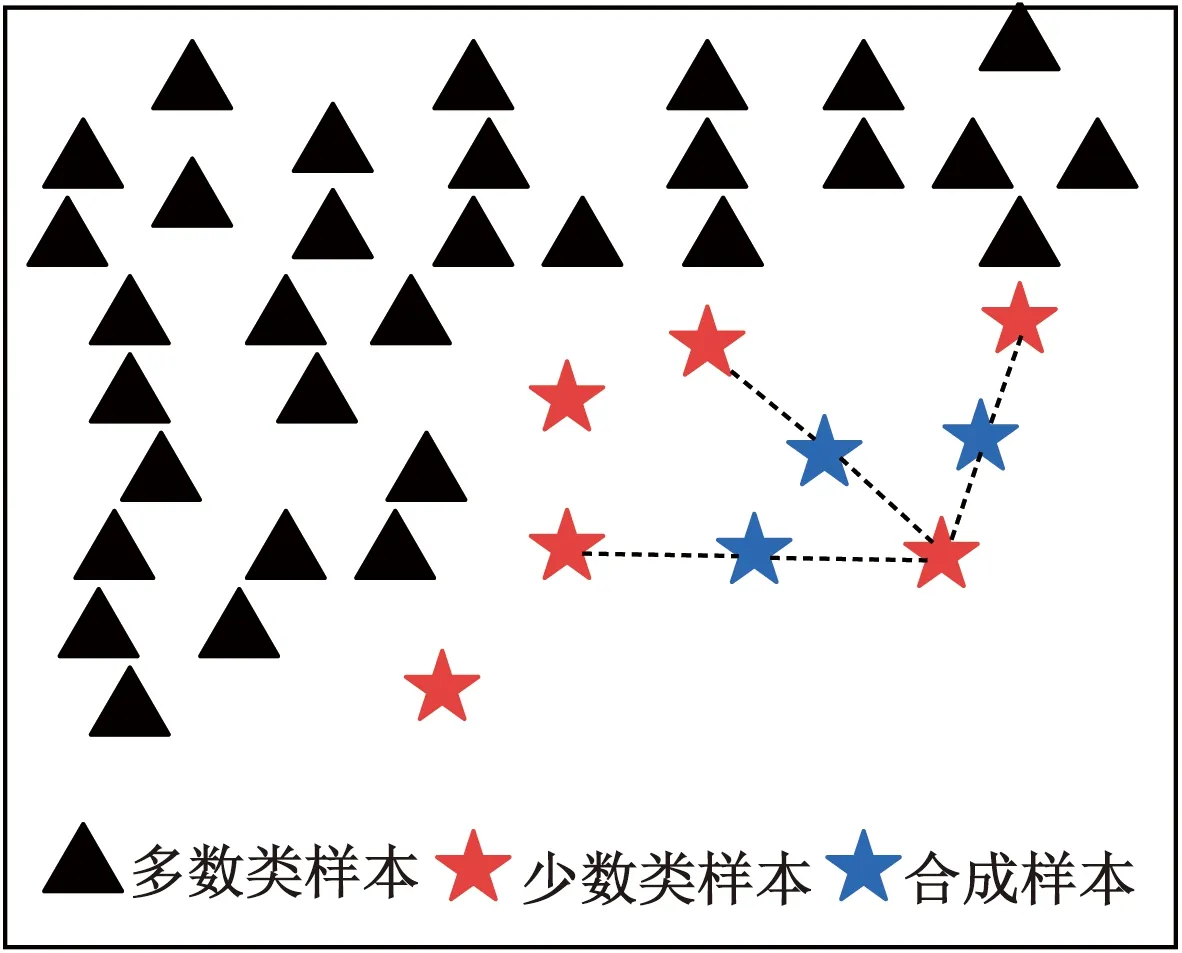
2 地震破坏模式参数分析

3 最佳参数筛选
4 地震破坏模式判别的两阶段模型


5 对比验证分析

6 结论

