基于流形距离的滚珠丝杠副性能评估
袁航, 雷振兴, 张会娟, 刘建娟
(河南工业大学电气工程学院, 郑州 450001)
滚珠丝杠副作为传动部件,在数控机床进给传动系统中,将旋转运动转化为高精度、高效率的直线运动。由于长时间承受高速运转、载荷冲击和加工粉尘等因素作用,不可避免地会出现磨损与退化现象,进而导致各种故障的发生,严重影响着机床加工精度和工件质量,甚至演变成整个机床的故障,给制造加工过程带来安全隐患。因此,在滚珠丝杠副的全寿命周期内,对其进行性能评估具有重要意义。依据评估结果,对其开展视情维修维护,进而降低故障发生风险与维护成本,提高设备运行的可靠性、安全性和经济性。
设备性能评估通过分析设备部件的各类型监测数据,如控制数据、过程数据、新增传感器数据等,实现其运行状态的识别与定量评价[1]。目前,滚珠丝杠副的性能评估可分为基于模型的方法和基于数据驱动的方法。基于模型的性能评估具有较高的准确度,但对复杂环境和系统建模较为困难,例如,Ni等[2]从设备失效机理分析,通过建立物理系统模型结合摩擦力矩以及接触应力来准确监测滚珠丝杠健康状况,但该方法易受到部件变化和故障类型多样性的影响。Zhou等[3]基于滚动轴承摩擦力矩的经验公式,提出了一种预测滚珠丝杠摩擦力矩和机械效率的新模型,但对于建立的非线性摩擦模型未考虑静态摩擦、库伦摩擦和黏滞摩擦等。基于数据驱动的性能退化评估技术以系统运行数据(如电压、电流、功率、振动、压力、温度等)为基础,从数据中挖掘隐含的信息,通过模型的学习进行评估,该类方法具有较强的适应性,但在评估精准度及运算效率方面具有较大提升空间。例如,赵帅等[4]从距离分析,通过对转矩信号拉普拉斯处理降维,采用马氏距离来表征滚珠丝杠健康度,在高维特征空间此种方法将受到限制;Zhang等[5]从能量分析,依据振动信号小波包能量和结合深度信念网络(deep belief network,DBN)深度学习方法划分滚珠丝杠副健康状态,但学习过程对运算性能要求较高,不适当的参数选择会导致学习收敛于局部最优解;Wen等[6]利用核密度估计概率分布结合变分自动编码器[7]深度学习方法来评估滚珠丝杠副的退化,在对信号压缩重构过程中会使得特征有所损失,并且需要大量数据来训练。
现通过对滚珠丝杠副滑块运动机理分析,利用加速度监测数据识别滑块运动状态,在此基础上,结合数据驱动方法,提取监测数据模糊熵以及时域特征指标来构建融合特征,进而在高维特征空间中计算流形距离,实现滚珠丝杠副的性能评估。该研究一方面考虑滚珠丝杠副滑块运动方向对其监测数据的影响,采用同向运动监测数据分析来降低评估误差;另一方面考虑监测数据的复杂性,采用高维空间流形距离进行距离计算,相对于欧氏距离与马氏距离,以期更好地从数据的空间结构去探索数据内部的本质特征。
1 理论分析
由于受到机械结构、材料特性、工作环境等因素的影响,在滚珠丝杠副全寿命周期的不同阶段,其故障模式与退化程度也各不相同,其中,润滑不足与粉尘污染是其常见故障类型。滚珠丝杠副在连续长时间运行过程中,若维护不及时,造成润滑不足或粉尘污染,设备性能会持续衰退,导致摩擦阻力增大,对应转矩不平顺程度增加,进而引发恒速保持能力降低,运行速度波动加剧,影响加工定位精度。
该研究所提出的滚珠丝杠副性能评估方法主要包括监测数据分段、多维特征提取、流形距离计算三大部分,具体如图1所示。首先,由于滚珠丝杠副的运动属于循环往复运动,振动加速度传感器所采集的振动信号包含多个正反向运动数据集,为提高评估准确性,针对正反向两种工况进行数据分段。之后,对数据分段后的正常信号和测试信号分别进行特征提取,所提取特征包含模糊熵特征和典型时域特征,进而基于所提取特征构建高维特征空间。最后,在高维特征空间中计算正常数据特征和测试数据特征之间的流形距离,再将计算得到的流形距离转化为置信值(confidence value,CV),获取滚珠丝杠副的健康度。
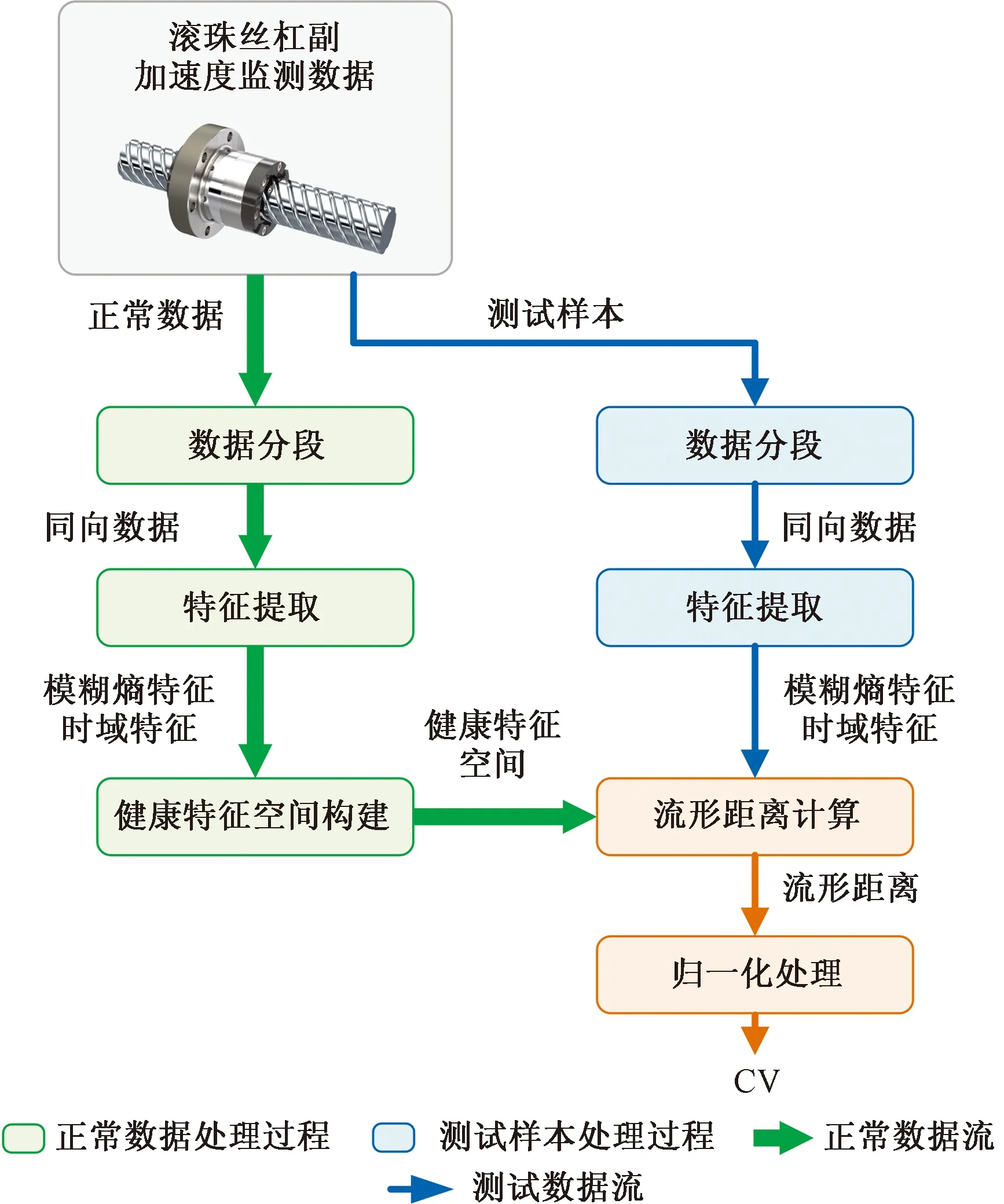
图1 滚珠丝杠副性能退化评估流程图Fig.1 Flow chart of ball screw pair performance degradation evaluation
1.1 数据分段
由于滚珠丝杠副的循环往复运动,其正反向行程数据存在一定的差异性,该研究对其正反向识别后分别进行评估,以此提高对滚珠丝杠副性能退化评估的准确性,数据分段算法流程如图2所示。
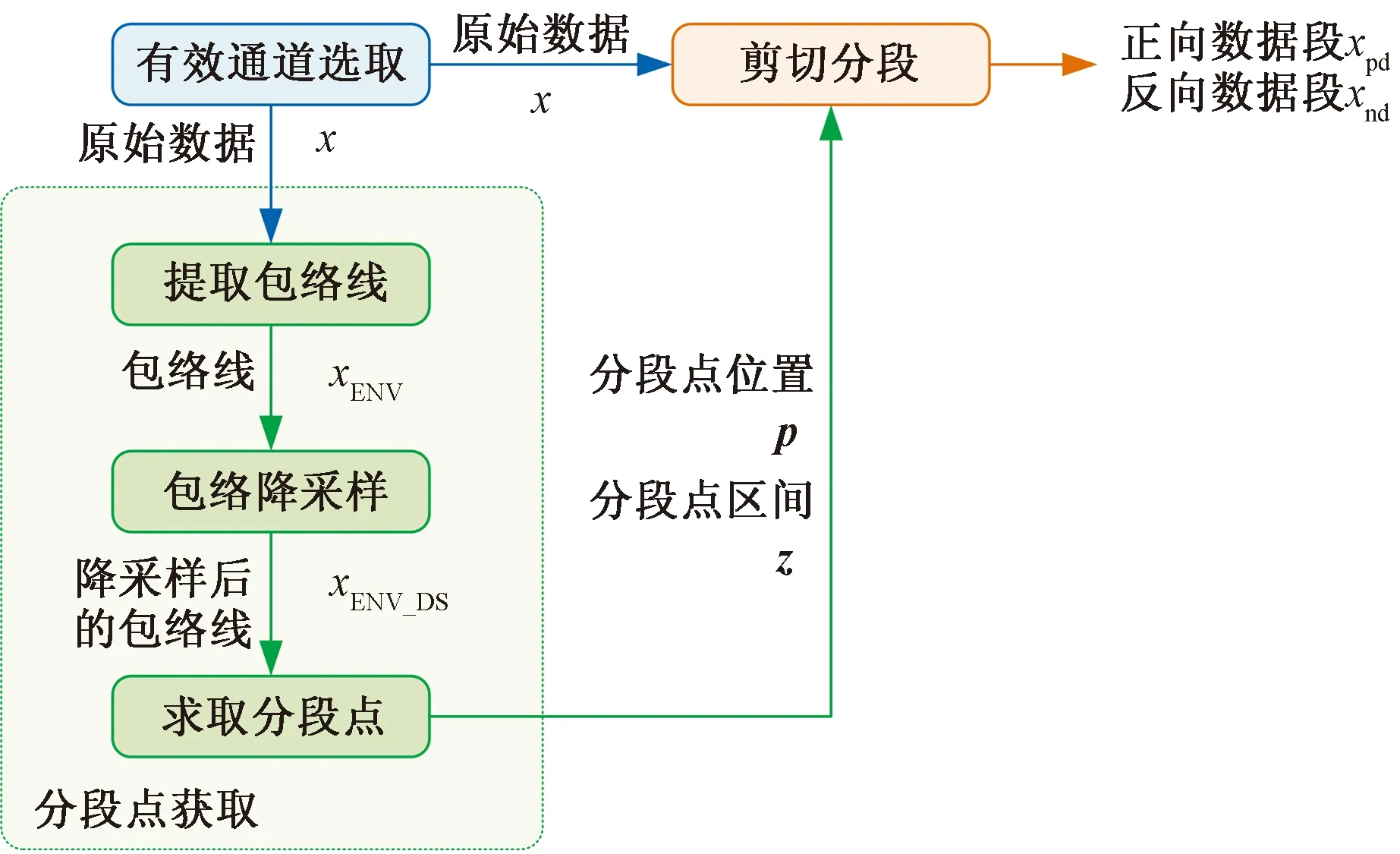
图2 数据分段流程图Fig.2 Data segmentation flow chart
原始数据分段点的位置确定分为两步,首先确定分段点区间,然后再确定分段点位置,该研究对滚珠丝杠副的分段点确定步骤如下。
1.1.1 输入
通道原始数据x,大小为Nt×1;期望段长L;其中Nt=fst,fs为采样频率,t为采样时间。
1.1.2 输出
正向数据xpd,大小为L×npd;反向数据xnd,大小为L×nnd;其中,npd和nnd分别为正向、反向数据段数,具体视信号情况而定。
1.1.3 中间变量
粗寻分段点位置集合为z,细寻分段点位置集合为p。
1.1.4 运算步骤
步骤1包络。
xENV=f1(x),其中,f1为RMS上包络函数,xENV大小为Nt×1。
步骤2降采样去重。
xENV_DS=f2(xENV,m),其中,f2为降采样函数,m为降采样率;xENV_DS大小为N×1,N=Nt/m。
xENV_DS_INC=f3(xENV_DS),其中,f3为升序排列函数,xENV_DS_INC大小为N×1。
S=f4(xENV_DS_INC),其中,函数f4通过去除重复元素,仅保留xENV_DS_INC中独立元素(多个重复仅保留一个元素)。
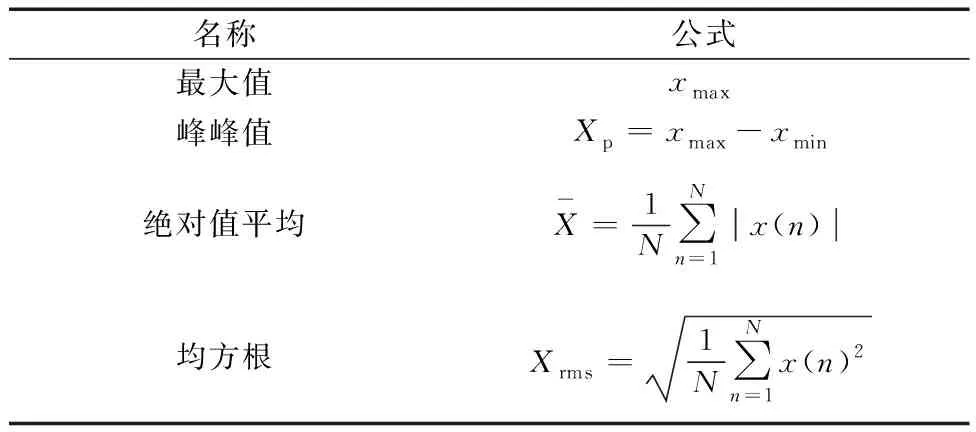
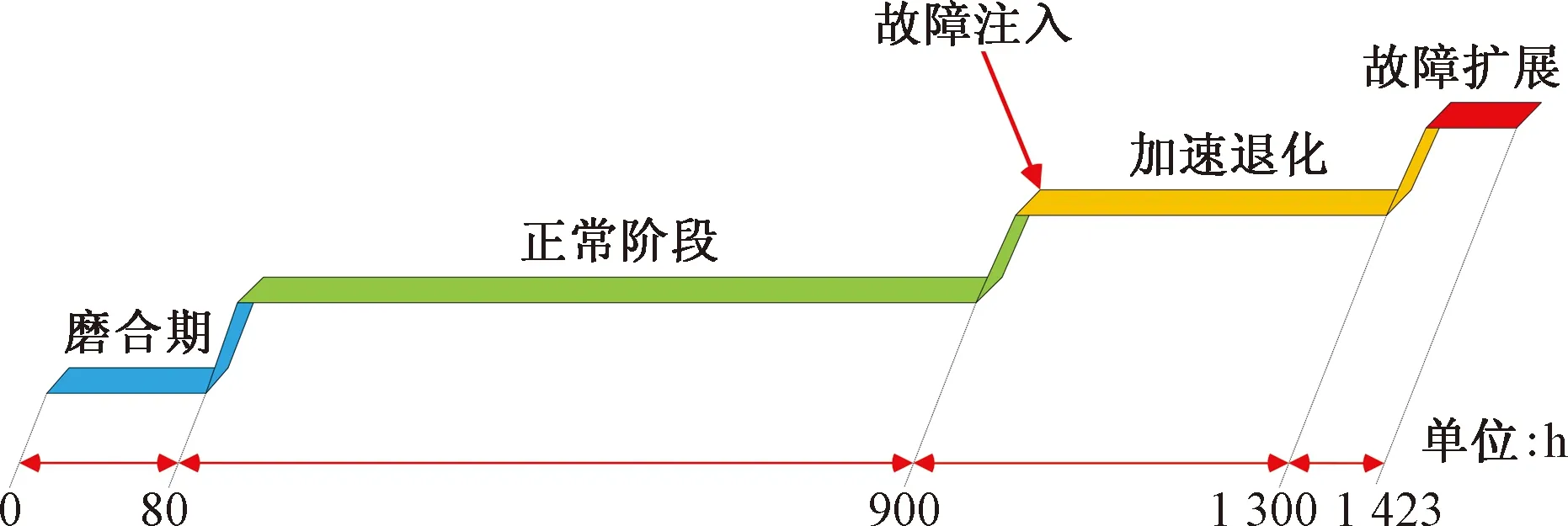
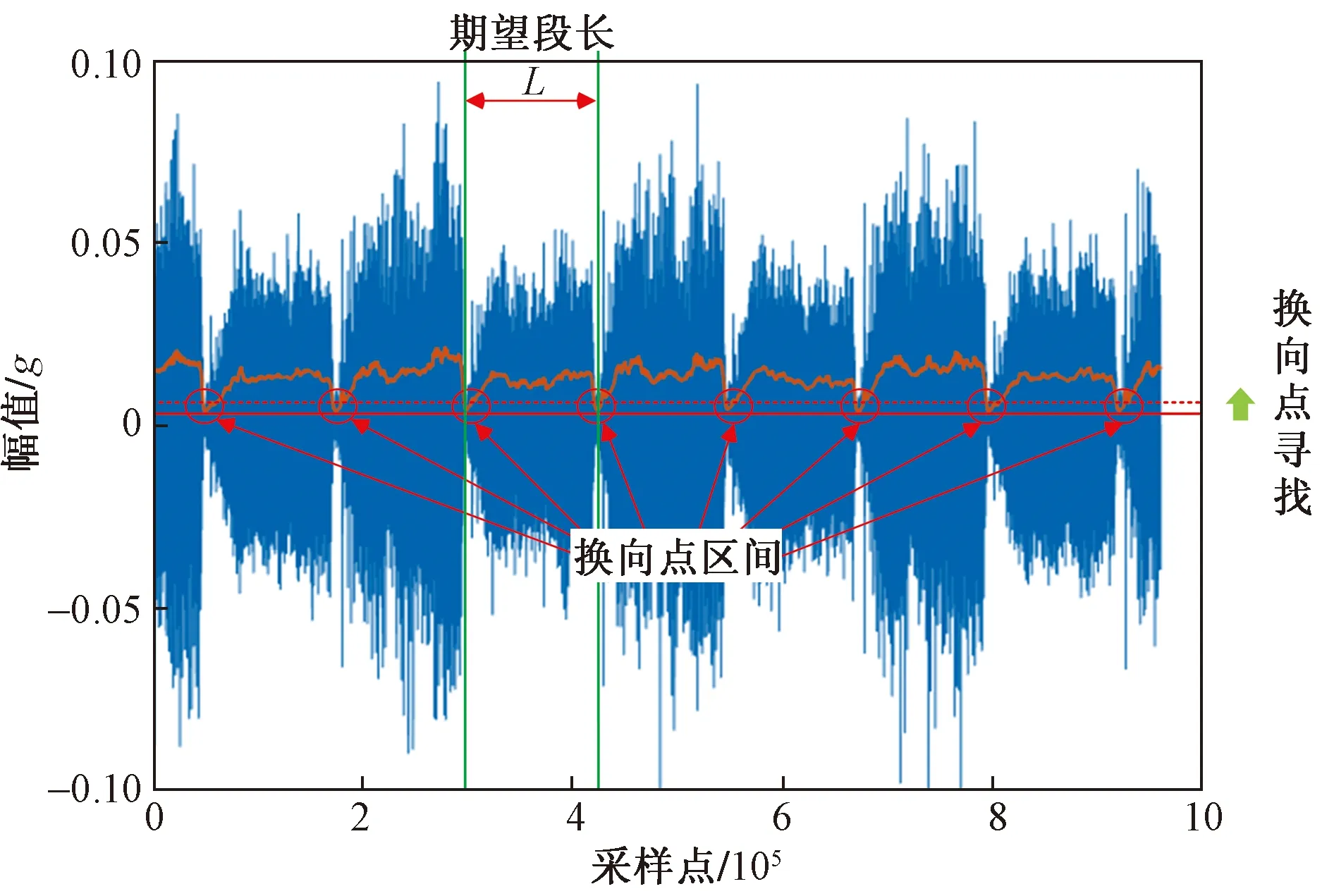
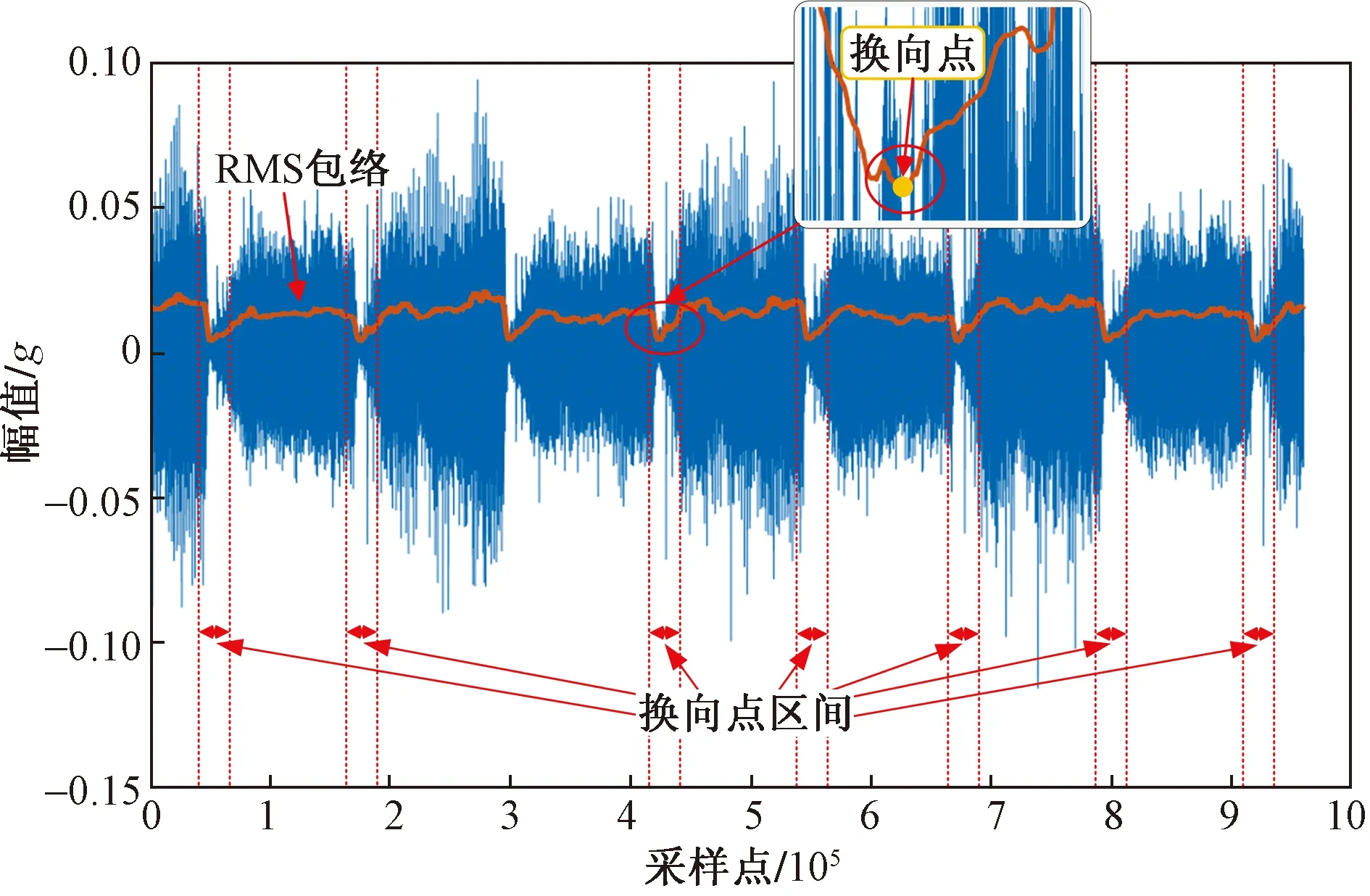
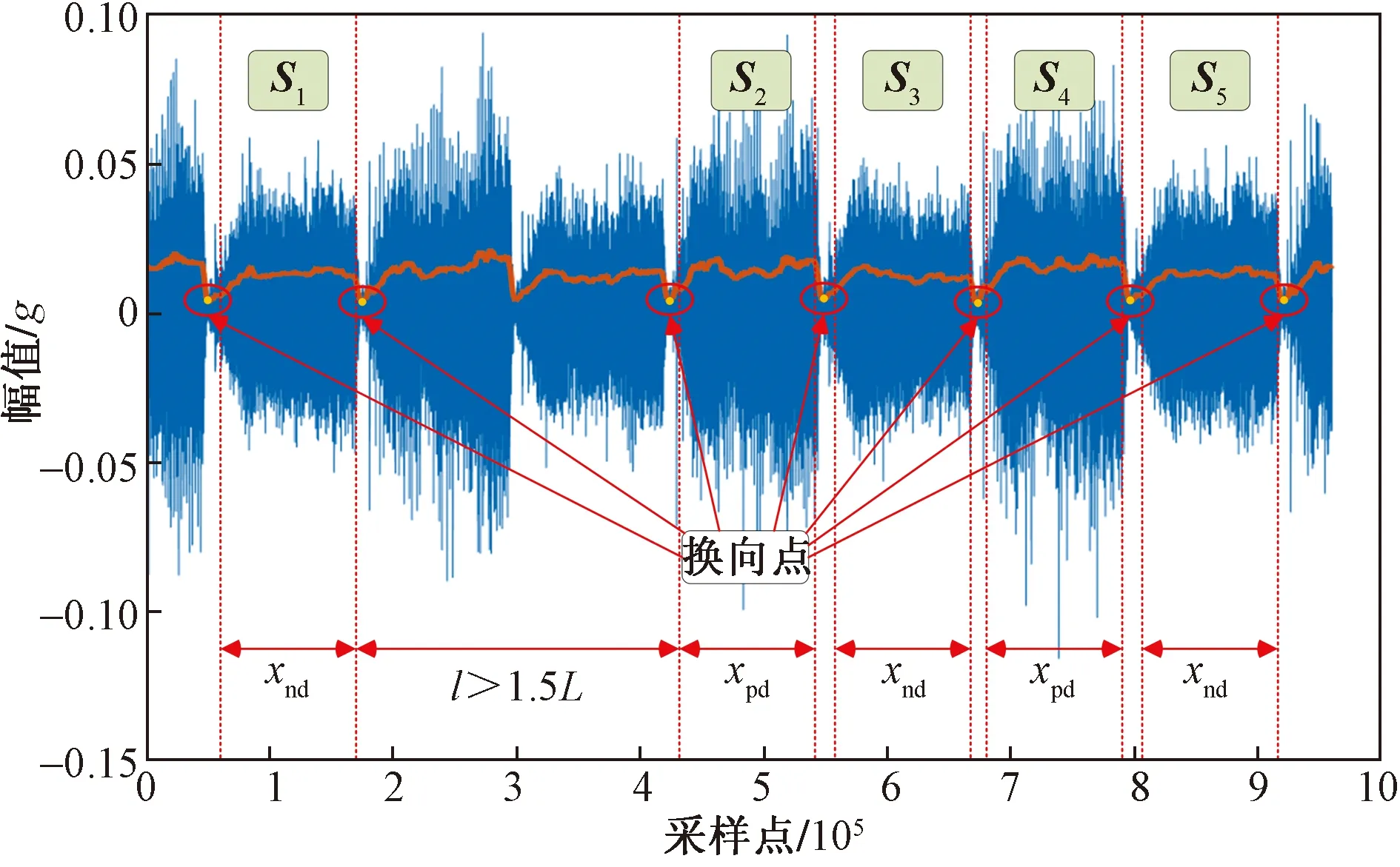
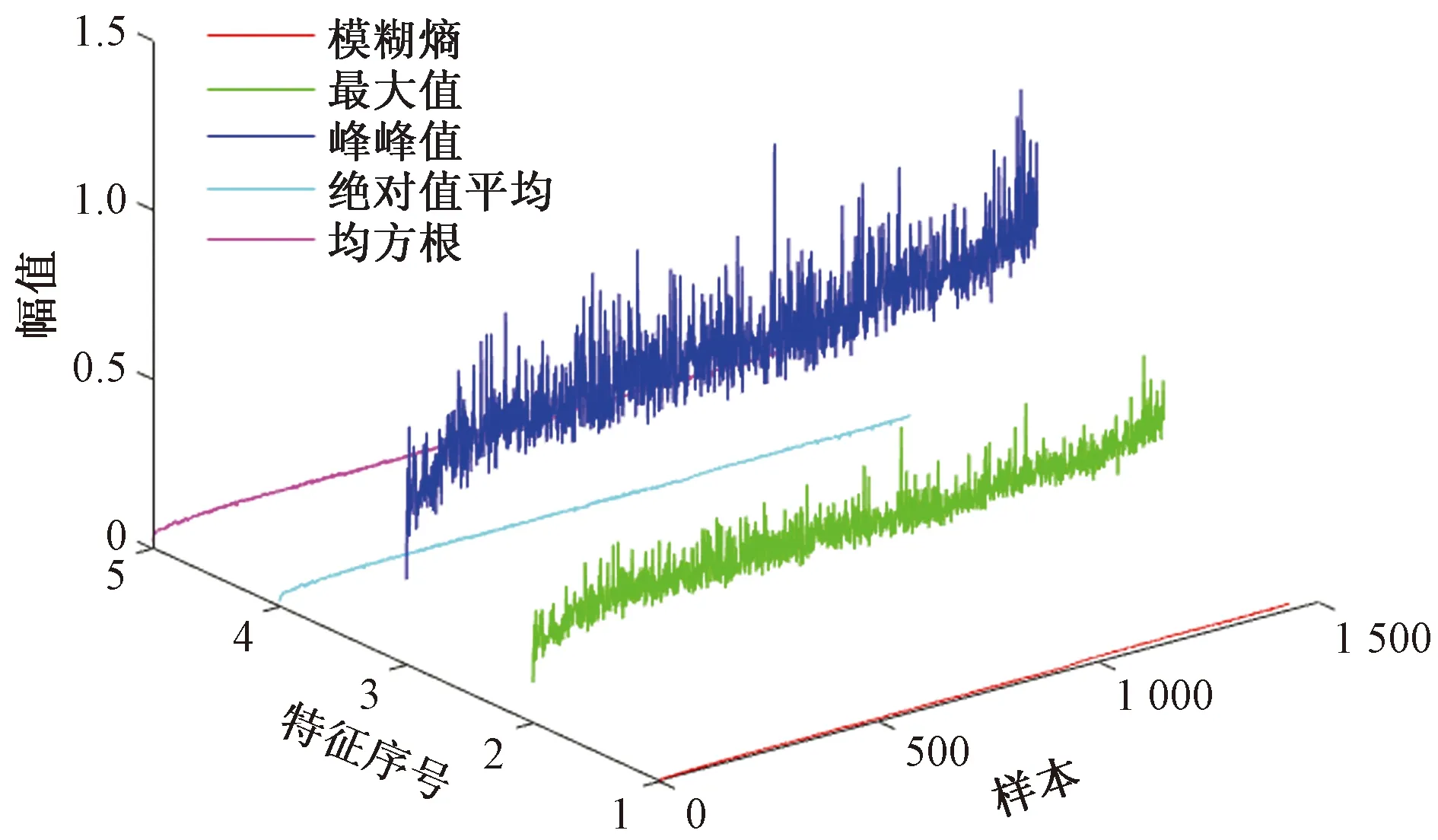
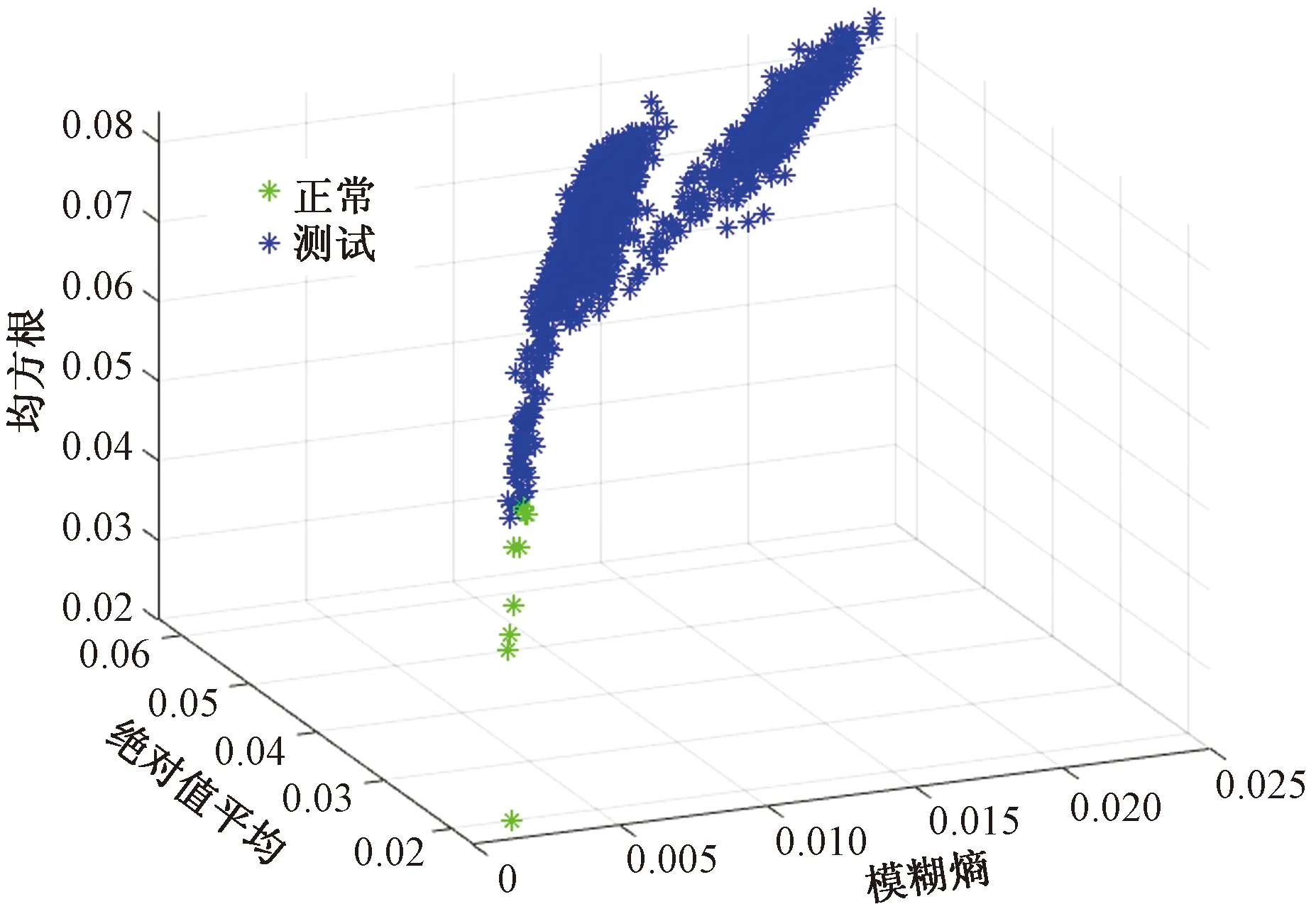
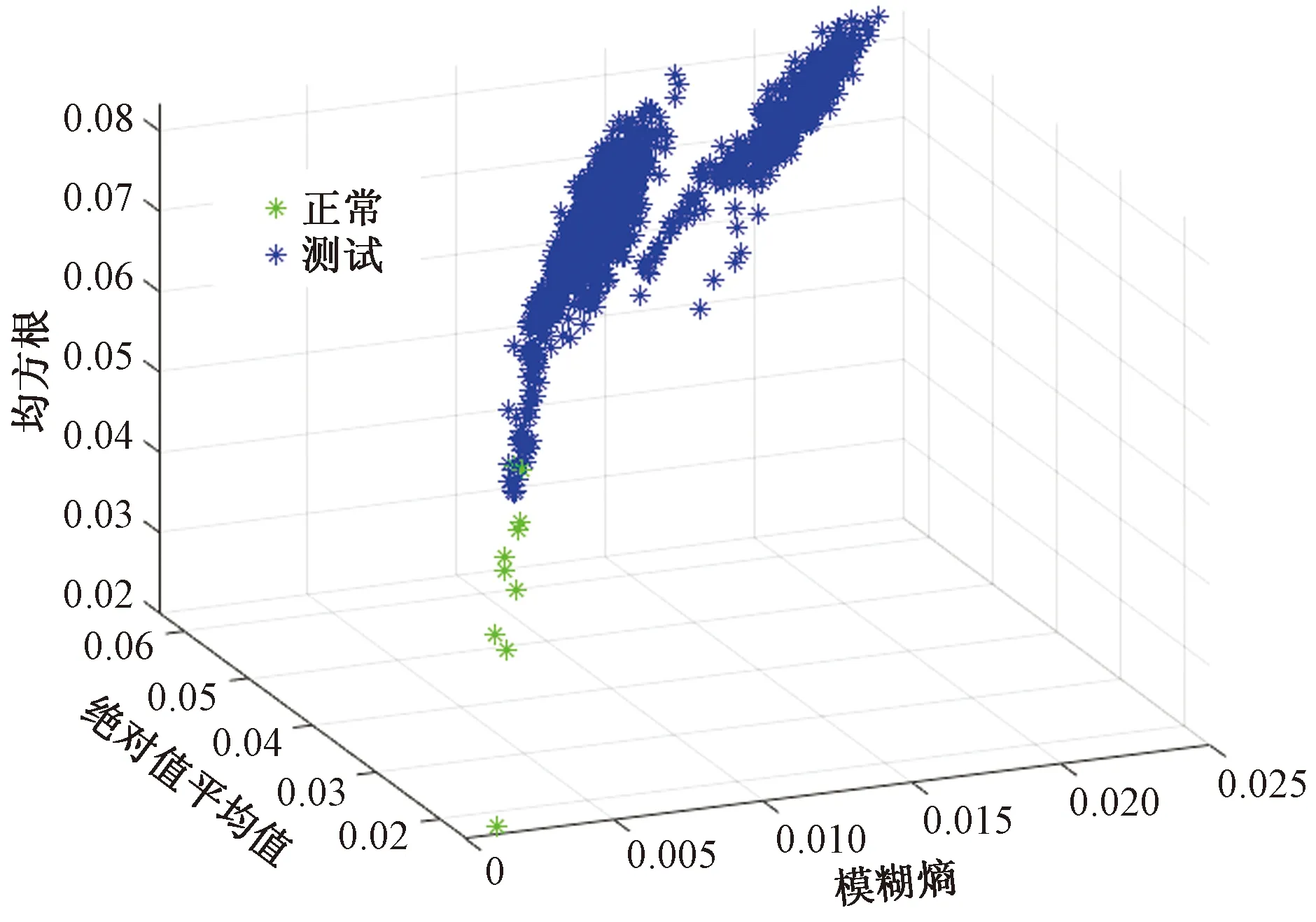
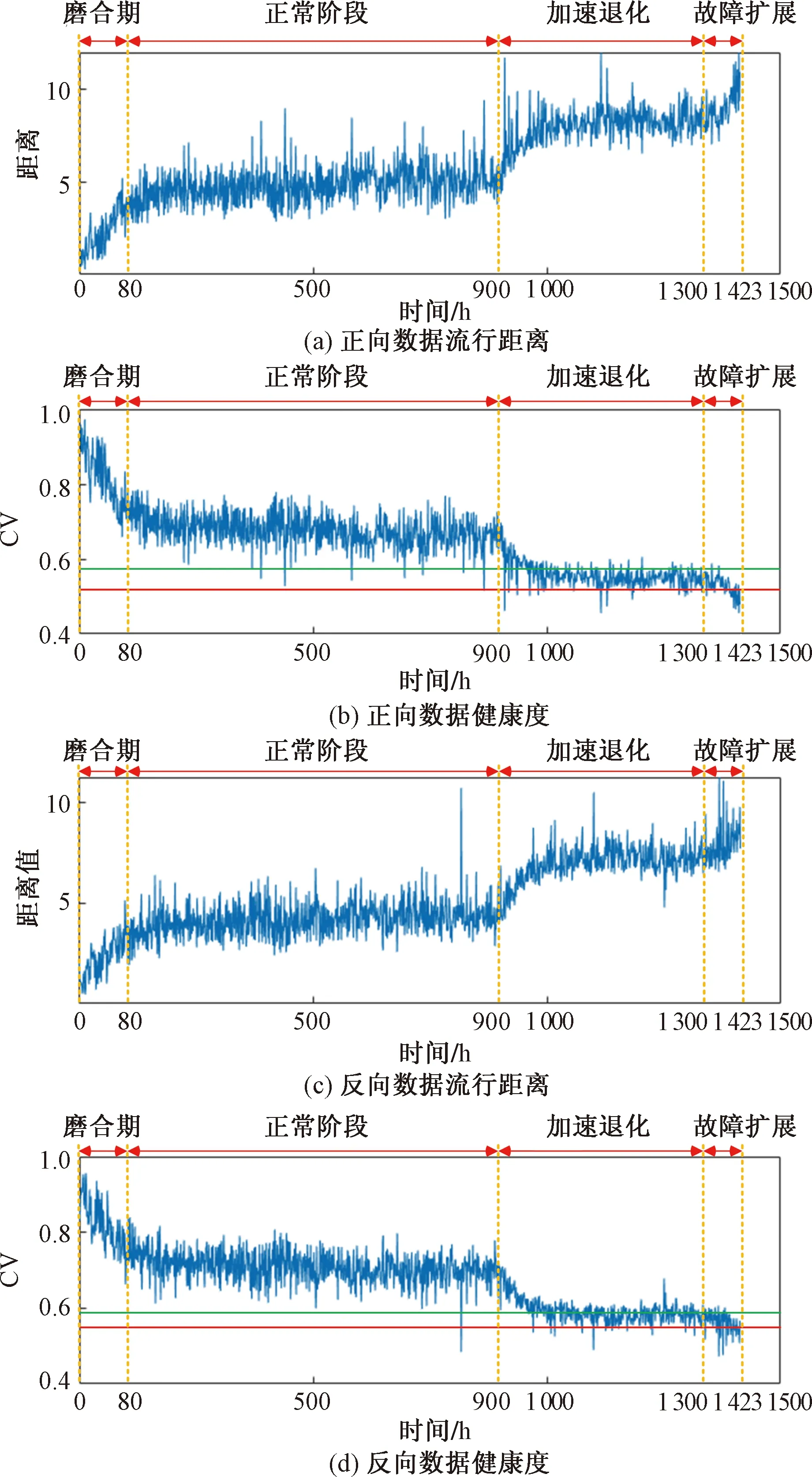
S=[s1,s2,…,sQ],S大小为Q×1,Q 步骤3粗寻分段点。 初始化: 定义水平线:y=s1。 定义:r=floor(Nt/L),其中,r为期望粗寻分段点个数(也即分段点区间个数)。 z1=f5(w1),其中,f5函数仅保留w1中相互距离不小于L/m的元素。 z=z∪z1,其中,z=[z1,z2,…]。 迭代: fori=1,2,…,Q y=si; zi=f6(wi); z=z∪zi; if length(z)==r break; end end 其中,f6函数仅保留wi中元素最小距离不小于L/m的元素。 步骤4细寻分段点。 由步骤1~步骤3可得到粗寻分段点位置集合z=[z1,z2,…,zr],大小为r×1。 forj=1,2,…,r lj=f7(zj); pj=f8(lj); p∪pj; end 其中,函数f7将粗寻分段点位置还原成位置区间,lj=[zjm-m,zjm-m+1,…,zjm+m-1]大小为2m×1;函数f8取位置区间所属数据最小值位置。 步骤5剪切分段。 由步骤1~步骤4可得到细寻分段点位置集合p=[p1,p2,…,pr],大小为r×1。 依据得到的分段点位置剪切分段原始数据,截取符合期望段长L的区间数据(相邻换向点距离满足L~1.5L,取相邻换向点中位数,在此中位数左右各截取L/2区间数据);采用邻域面积比较法对区间数据进行判定时,规定面积数值大的为正行程区间数据xpd,面积小的为负行程区间数据xnd。 确定分段点区间(也即粗寻分段点)操作示意图如图3所示,单行程数据量为两分段点间数据段,各单行程段长基本相等。取粗寻分段点过程中期望数据段长为L/m,Dmin为水平线与包络线单个交点到原分段点的最小距离,由于原始数据起始位置影响,分段点区间个数(也即粗寻分段点个数)从重采样RMS包络线波谷个数确定。 图3 分段点区间的确定示意图Fig.3 Schematic diagram for determination of subsection point interval 确定分段点位置(也即细寻分段点)如图4所示,在分段点区间上确定的最小值位置即为原始数据的一个分段点位置。 图4 分段点位置的确定示意图Fig.4 Schematic diagram for determining the position of subsection points 依据得到的分段点位置剪切分段原始数据,如图4所示,截取相邻分段点符合期望段长L的区间数据时,取符合期望段长L的相邻分段点中位数,在中位数左右各截取L/2的区间数据,L≤xpd<1.5L,L≤xnd<1.5L。 采用邻域面积比较法对相邻分段点区间数据进行判定,规定面积数值大的为正行程区间数据,面积小的为反行程区间数据,如图5所示,相邻面积比较S1 图5 剪切分段示意图Fig.5 Sectional diagram of shearing 为了监测滚珠丝杠副的状态,需要利用多个特征尽可能准确表征滚珠丝杠副从正常状态到失效状态的退化趋势。随着滚珠丝杠副的持续运行,滚珠与滚道润滑逐渐不足,会产生一系列异常振动信号,采用合适的特征提取方法提取出敏感度高、表征性强的特征,可有效提高滚珠丝杠副的故障诊断和性能评估的准确性。该研究对滚珠丝杠副的性能评估采取多特征融合的方法[8],从多个角度提取表征滚珠丝杠副性能退化的相关特征。 1.2.1 模糊熵特征 熵作为一种统计测度,通过考虑时间序列的非线性行为来量化复杂性并监测动态变化[9]。随着非线性科学的发展,近年来多种非线性分析方法,如近似熵、样本熵、排列熵等已广泛应用于机械故障诊断领域。与传统分析方法相比较而言,基于熵的方法具有聚类能力强、分类精度高、抗噪声能力强以及不依赖先验知识等优点[10]。模糊熵(fuzzy entropy,FE)在样本熵和近似熵的基础上发展而来,利用模糊隶属度函数代替常规熵中的硬阈值判据,充分利用其模糊信息处理能力,增强了统计效果的稳定性。模糊熵衡量的是新模式产生的概率大小,该值越大,新模式产生的概率越大,序列复杂度越大,将该特征应用于滚珠丝杠副状态表征,即与正常状态偏离度越大,因此,模糊熵可较好地利用振动监测数据对滚珠丝杠副的性能状态进行表征。 假设给定的时间序列为{Xi}={x1,x2,…,xN},模糊熵FuzzyEn计算过程如下。 步骤1对于给定的时间序列为{Xi}={x1,x2,…,xN}按顺序以m为窗,将时间序列分为k个序列,其中k=N-m+1。 (1) (2) uj(t)]|},k=0,1,…,m-1; i,j=1,2,…,k且i≠j (3) (4) 式(4)中:r为相似容限参数,定义为原一维时间序列标准差的R倍,即r=Rδ。 同时,对除自身以外所有隶属度求平均,公式为 (5) 步骤4将窗m增长为m+1,重复步骤1~步骤4。 步骤5计算模糊熵。 FuzzyEn(t)=ln[φm(t)]-ln[φm+1(t)] (6) 1.2.2 时域特征 在机械设备状态监测、故障诊断与健康管理过程中,时域信号作为振动试验获得的原始信号,保留了最全面、最完整的信息[11]。在时域分析方法中,信号的基本统计特征和概率分布可划分为有量纲指标和无量纲指标。如表1所示,研究针对所采集滚珠丝杠副振动数据,提取能较好反映其故障退化的典型时域特征指标最大值、峰峰值、绝对值平均、均方根来进行融合特征评估。 表1 典型时域特征指标Table 1 Typical time domain characteristic index 最大值和峰峰值反映了信号的振幅波动情况,适用于检测具有瞬时冲击的故障类型;绝对值平均反映了信号振动幅度的平均水平,适合监测磨损类故障;均方根反映了信号的能量大小,为二阶矩,可反映振幅随时间的缓慢变化,而磨损也是一种由缓及重的变化过程,因此均方根可用来表征滚珠丝杠副的磨损程度。 通过比较待评估样本的特征向量和标准健康样本的特征向量之间的距离,或者二者之间的相似度来评估健康度是目前较为常用的设备性能评估方法之一[12]。常用的有欧氏距离、马氏距离、余弦相似度等方法。欧氏距离将样本的不同属性(即各指标或各向量)之间的差别等同处理,在样本距离较近时,易互相干扰,影响评估准确度。马氏距离[13]表示数据的协方差距离,它是一种有效的计算两个未知样本集的相似度的方法,马氏距离不受量纲影响,还可以排除变量之间的相关性的干扰,但受局部微小变量影响较大,对全局性反映不足。在高维空间中,为了克服欧氏距离与马氏距离的不足,该研究引入流形距离对滚珠丝杠副进行性能评估。 流形学习[14]从数据的空间结构去深度挖掘数据内部的本质特征,简化了数据的复杂度。流形距离[15]使用了微分几何中测地线的思想,它计算数据从高维空间在向低维空间映射之后流形上的测地线距离。流形距离评估计算步骤如下。 步骤1假定高维数据集X由n个样本组成,X={x1,x2,…,xn},定义L(xi,xj)为样本xi与xj之间在流形空间上的直线长度。 L(xi,xj)=ρdist(xi,xj)-1 (7) 式(7)中:dist(xi,xj) 为样本xi与xj之间的欧氏距离;ρ>1为收缩膨胀系数。 步骤2建立近邻图。将数据视为加权图G=(V,E)的顶点V,将边集E={Wij}视为每对数据点之间定义的流形长度。p={p1,p2,…,pl}∈Vl,p1与p2的边界(pk,pk+1)∈E,1≤k 步骤3计算最短路径。 (8) 式(8)中:L(pk,pk+1)为xi与xj之间路径的流形长度。 步骤4流形距离归一化,转化为置信值。 (9) 式(9)中:di为计算得到的流形距离;a为可调整的归一化参数,通过调整参数a,可以调整CV对故障不同阶段的敏感程度。 如图6所示,滚珠丝杠副试验台包括伺服驱动器、伺服电机、滚珠丝杠副和控制电路。使用4个加速度传感器采集振动数据,传感器1安装在滑块顶部与地面垂直方向,传感器2安装滑块侧面与轨道垂直方向,传感器3安装在轨道中点侧面与轨道垂直方向,传感器4安装在轨道支承座端部。试验采用的加速度传感器为IEPE型,量程50g(g为重力加速度),灵敏度100 mV/g,所采集信号为电压信号。丝杠直径为16 mm,导程为10 mm,有效行程100~1 500 mm,定位精度0.02 mm。伺服电机额定转速3 000 r/min,环境温度为室温。 图6 滚珠丝杠试验台Fig.6 Ball screw test bench 设定滚珠丝杠副滑块往返运动区间长度为50 cm。振动数据每60 min采集一次,采样率为32 kHz,每次采样时间为30 s。试验操作运行流程时间如图7所示,试验开始前用清洗剂对丝杠清洗处理,试验开始后重新加入润滑脂,连续运行,从0 h开始采集监测数据。为了模拟工业现场粉尘污染对滚珠丝杠副的影响,在试验的第900 h开始,对试验台的丝杠及滑块加入典型工业粉尘颗粒大小10 μm的铁粉。 图7 试验时间轴Fig.7 Test timeline 2.2.1 数据分段 试验中针对4个通道采集数据发现4号加速度传感器通道数据适合数据分段,2号加速度传感器通道数据适合做评估。由于原始数据量过于庞大,对滚珠丝杠副性能评估时,原始数据多个正反行程只选取第一次正向和第一次反向数据,并每8个点对原始数据进行重采样,重采样后每12 500个点进行特征提取。该研究将试验数据集的前10 h的数据(第1~10组数据)作为正常情况,后续1 423 h数据(第11~1 433组数据)做测试评估。 根据滚珠丝杠副4号加速度传感器通道数据,粗寻换向点区间个数及期望段长的确定如图8所示,换向点位置的确定如图9所示。依据换向点位置信息,数据剪切分段结果如图10所示。 图8 换向点区间确定示意图Fig.8 Schematic diagram for determining reversing point interval 图9 换向点位置确定示意图Fig.9 Schematic diagram for determining reversing point position 图10 剪切分段示意图Fig.10 Sectional diagram of shearing 2.2.2 特征提取 对每一组数据提取模糊熵特征,最大值、绝对值平均、峰峰值、均方根时域特征,归一化之后进行流形距离计算。如表2所示为部分试验提取特征结果,其中正常数据和测试数据正反向各选取了连续3组,由于试验采用加速度传感器采集电压信号,将其转换成加速度后会更小。图11、图12为研究所提取的5种特征指标。其中,选取模糊熵、绝对值平均、均方根在三维空间内聚类效果如图13、图14所示。 图11 正向特征提取结果Fig.11 Forward feature extraction results 图12 反向特征提取结果Fig.12 Reverse feature extraction results 图13 正向数据特征模糊熵、绝对值平均、均方根三维效果Fig.13 Three-dimensional effect of fuzzy entropy, absolute value average and root mean square of forward data features 图14 反向数据特征模糊熵、绝对值平均、均方根三维效果Fig.14 Three-dimensional effect of fuzzy entropy, absolute value average and root mean square of reverse data features 2.2.3 性能评估 在获取模糊熵和时域特征后,通过计算流形距离得到正常数据和测试数据的流形距离,然后将得到的距离进行归一化,将流形距离转化为表示滚珠丝杠副健康状态的CV。 图15(a)和图15(b)分别为正向正常数据和测试数据之间的流形距离和CV。受到机械装配精度影响,起始段0~80 h为新设备初始投入使用“磨合期”,磨合期过后滚珠丝杠副运行平稳,进入80~900 h“正常”阶段。依据经验,健康状态阈值选择为0.68,亚健康状态阈值为0.59,由于滚珠丝杠副设备从投入使用到完全故障退化周期较长,试验考虑在丝杠导轨加入直径10 μm铁粉,加速退化试验。因此从健康状态运行约900 h后注入故障,从900~1 300 h由于注入了加速磨损故障,设备进入“加速退化”阶段,健康度下降,后续进入短暂稳定期。加速磨损退化阶段由于设备继续长时间运行,1 300~1 423 h故障损伤逐渐显现积累,设备进入“故障扩展”阶段,随着运行时间加长设备健康度继续下降,CV下降到0.56以下。图15(c)和图15(d)为滚珠丝杠副正反向性能退化流形距离和CV评估对比。 图15 正反向流形距离和CV值对比Fig.15 Comparison of forward and backward manifold distance and CV value 提出了一种基于数据分段、模糊熵、时域特征和流形距离的滚珠丝杠副健康评估方法。该方法对往复运动的非线性振动信号具有良好的适用性。利用数据分段可以将原始信号分为正向和反向,从而更精确评估滚珠丝杠副的健康状态。在数据分段完成后,针对单方向原始数据提取模糊熵和典型时域特征构建特征空间,再利用流形距离计算距离,然后将流形距离归一化为CV,从而得到滚珠丝杠副的健康程度。试验表明,数据分段、模糊熵与时域特征融合和流形距离可以有效地表征滚珠丝杠副的退化过程和健康程度。然而,该研究在特征提取方面还有一定的不足,后续,将通过多维度方法,挖掘深层次的故障信息,以便于在更深层次对滚珠丝杠副故障状态进行表征,以此来提高性能评估准确性;除此之外,还将开展多工况、复杂环境下的滚珠丝杠副性能评估。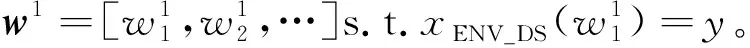



1.2 特征提取
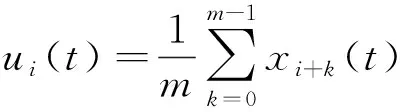
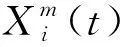

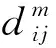
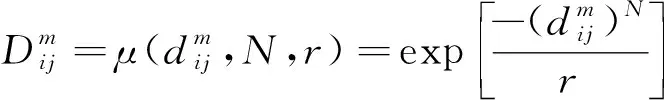
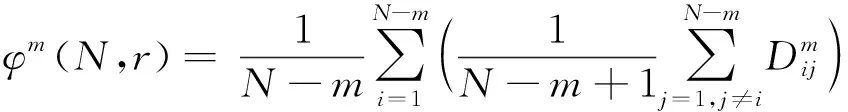
1.3 流形评估


2 试验验证
2.1 试验设置

2.2 数据分析

3 结论

