基于多特征融合与机器学习的井架钢结构智能诊断

黄岩, 韩东颖*, 朱国庆, 时培明

(1.燕山大学车辆与能源学院, 秦皇岛 066004; 2.燕山大学电气工程学院, 秦皇岛 066004)

井架钢结构是石油钻机八大系统的重要组成部分,属于大型承载钢结构[1]。随着二次采油、三次采油和海洋油气钻探等的迅速发展,井架钢结构在长期恶劣的野外环境中作业,并且受到频繁搬迁、安装过程中各种因素的影响[2]。根据长期实践经验,研究者发现此时井架钢结构的内部结构会逐渐产生不同程度的腐蚀、变形、疲劳等损伤,且这些损伤几乎都是从节点破坏开始的,较少是由于结构整体刚度或强度不足引起,这给钻采作业带来了潜在安全隐患,所以对井架钢结构进行智能诊断对避免安全事故具有重大意义[3]。

与正常井架钢结构相比,存在损伤的井架钢结构在冲击力的作用下,其各点加速度信号的时域分布会有所变化,而在振动下产生的加速度信号具有非平稳性和非线性,传统的方法和单一的时域特征无法反映其整体变化[4-5],故需对多个特征进行融合。主成分分析法(principle component analysis,PCA)[6-8]在1901年由皮尔逊提出,属于因子分析的一种[9]。PCA主要运用了降维思想,将多个特征通过计算的方法融合,提取出少数几个不相关的或一个可以代表特征大部分信息的新特征。在应用此方法时,无需考虑各传感器间以及各原始特征间的相关性对损伤识别结果的影响,从而获得一个相对平衡的新的综合性特征。支持向量机(support vector machine,SVM)是90年代中期发展起来的以统计学习为基础的机器学习方法[10-11],通过探求结构化风险最低以提高学习机器的泛化能力,实现结构风险的最小化,是识别井架钢结构损伤的理想方法。

现结合时域多参数信息融合与机器学习,利用主成分分析法将多个时域特征融合成为一个归一化的特征,以此作为损伤识别支持向量机分类器的输入向量,实现针对井架钢结构单一损伤位置和多损伤位置快速、准确的识别,并对井架钢结构进行建模与仿真计算,通过实验室井架钢结构进行模拟试验,验证方法的可行性。

1 时域多参数信息融合与机器学习

1.1 时域多参数信息融合方法

在进行时域多参数信息融合时采用主成分分析法,其原理是将原来的多个特征做线性组合作为新的综合特征,将线性组合根据所包含信息的多少进行降序排列,排列后的第一个线性组合即为第一主成分[12]。其中信息由线性组合的方差来表示,即第一主成分的方差最大,表示第一主成分包含的信息最多。选取两个特征的具体分析过程对主成分分析法的步骤进行如下说明。

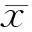
(1)

式(1)中:M为样本数量;xi为第i个样本值。

步骤2求协方差矩阵C。表达式为

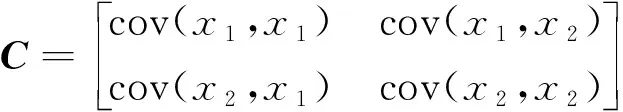
(2)

式(2)中: cov(x1,x1)为特征x1的方差;cov(x2,x2)分别为特征x2的方差;cov(x1,x2)、cov(x2,x1)分别为特征x1和x2协方差。

协方差大于0时,两特征数值呈正相关,协方差小于0时,呈负相关,且协方差的绝对值越大,两者对彼此的影响越大,反之越小。其中,cov(x1,x1)的求解公式如下,其他类似。

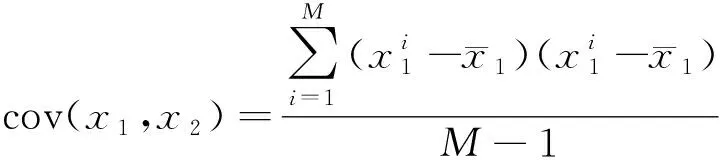
(3)

步骤3求协方差矩阵的特征值λ和特征向量μ。表达式为

Cμ=λμ

(4)

特征值会有N个,每一个特征向量对应一个特征值,在信号处理中,认为信号具有较大方差,而噪声具有较小方差,则将特征值按照降序排列,选取前k个,则会得到对应的一组矩阵{(λ1,μ1),(λ2,μ2),…,(λk,μk)}。原始特征只有两维,则令k=1可得最大的λ1和其对应的μ1。

步骤4将原始特征投影到选取的特征向量上,得到处理后新的综合性特征。计算公式为

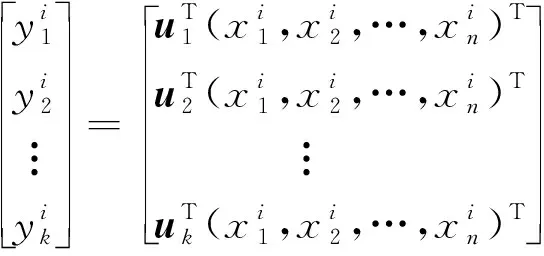
(5)

1.2 机器学习方法

在进行损伤识别的过程中采用机器学习方法中的支持向量机,它是一种二分类模型,在解决非线性、小样本、高维模式识别以及局部极小等问题中具有许多特有优势,是理想的模式识别方法[13]。SVM将低维空间中的不可分问题转化至高位空间内进行解决,寻求一个最优的分类面[14-17]。

SVM基于已有的训练集D={(x1,y1), (x2,y2),…, (xm,ym)},yi∈{+1,-1},在该训练集的样本空间内寻求一个最优超平面,使得样本数据被划分为两类,且两类样本数据到该平面的距离之和为各超平面中最大的。当样本线性可分时,寻求的超平面和最优超平面分别如图1所示。

图1 最优超平面示意图Fig.1 Schematic diagram of the optimal hyperplane

在训练集样本空间中,决定超平面的方程如式(6)所示,由于该超平面由w和b确定,所以记该面为(w,b),则训练集样本空间中的样本点到该超平面的距离如式(7)所示。

wTx+b=0

(6)

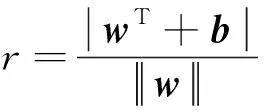
(7)

式中:w=(w1,w2,…,wd)为决定超平面的法向量;b为超平面到原点的距离。

距离超平面最近的几个训练样本被称为支持向量,使两个不同类支持向量到超平面的距离之和最大的超平面即为最优超平面[18]。

当训练集样本线性不可分时,则引入核函数将原来的空间映射到更高维的空间内,使其线性可分。本文选用的是径向基函数(radical basis function,RBF),识别原理示意图如图2所示,核函数映射如图3所示。

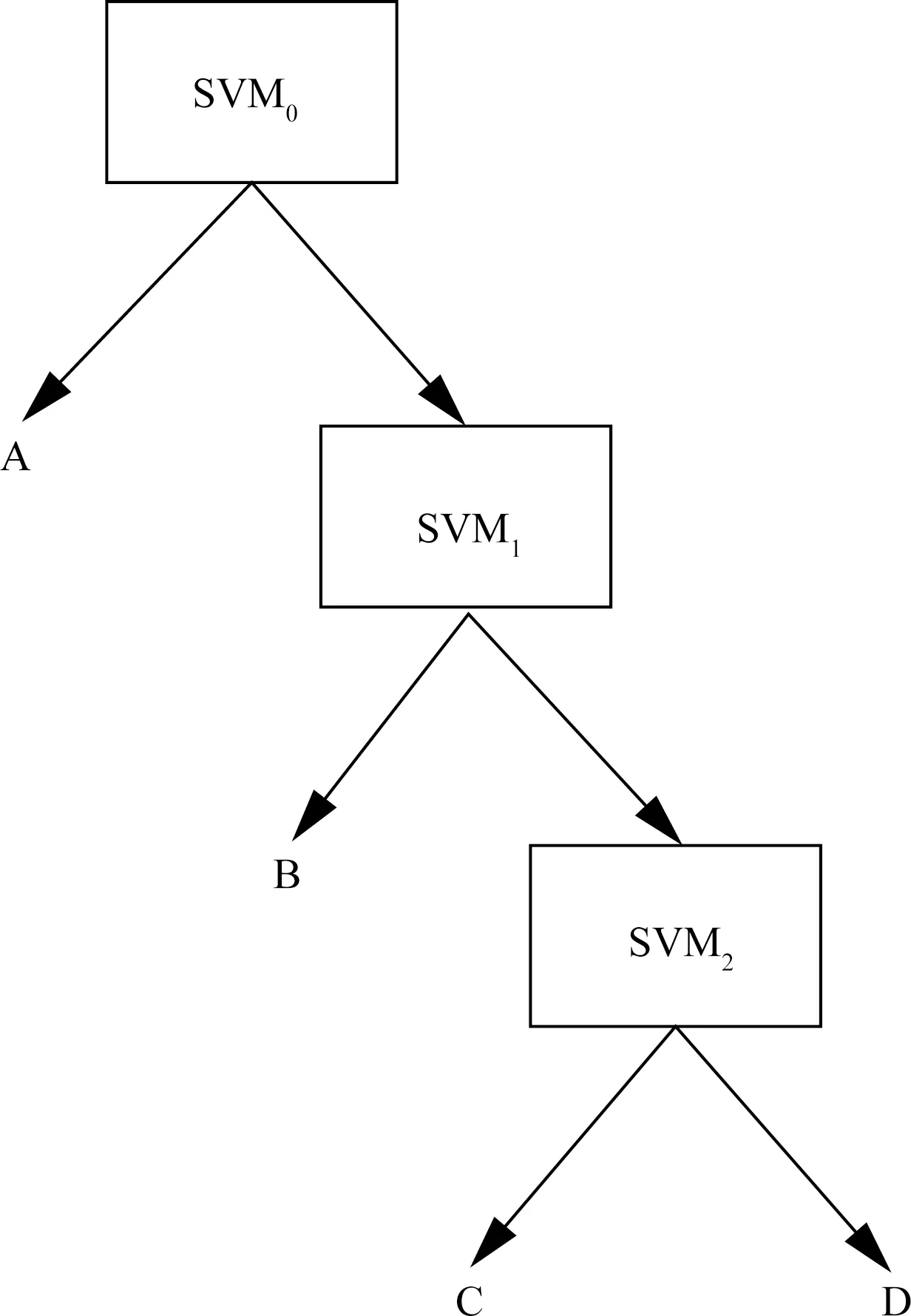
A为类型A;B为类型B;C为类型C;D为类型D;SVM0为支持向量机第一次分类;SVM1为支持内量机第二次分类;SVM3为支持向量机第三次分类图2 识别原理示意图Fig.2 Schematic diagram of identification principle

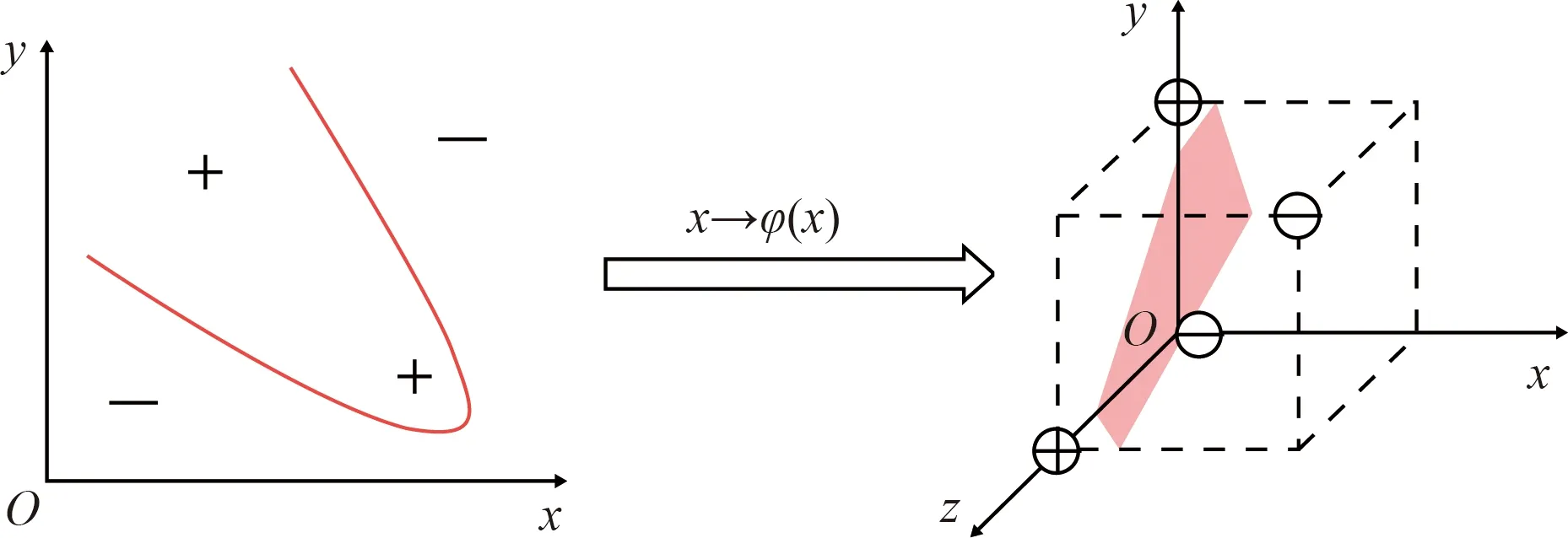
图3 核函数映射示意图Fig.3 Schematic diagram of kernel function mapping

2 提取井架钢结构信号特征

ZJ70型井架钢结构实验室模型高度为2.95 m,整体材料为Q235钢,其属性如表1所示。根据该模型参数建立仿真模型,井架钢结构模型节点位置如图4(a)所示,由上到下共设置20个节点。井架钢结构在工作过程中,其立柱和斜撑比较容易受到损伤[1],故选取的井架钢结构模型损伤单元编号如图4(b)所示,由上至下共设置3个损伤单元。

表1 ZJ70型井架钢结构材料属性Table 1 Material properties of ZJ70 type derrick steel structure

图4 井架钢结构模型编号示意图Fig.4 Schematic diagram of model number of derrick steel structure

2.1 井架钢结构模型分析

根据实验室井架钢结构模型参数建立井架钢结构的有限元模型,仿真模型建立过程中根据截面参数的不同设置21种截面属性,模型共分为292个梁单元,235个节点,其中2个固定铰支点(井架钢结构支脚处),其余均为刚性节点。对其施加冲击载荷进行激励,冲击载荷大小为200 N,载荷作用时间为1×10-4s,载荷作用位置与方向如图5所示,即右前立柱顶端,Y轴负方向。在无损伤状态下随机选取3号节点某一次模拟为例得到的加速度响应信号如图6所示,对应实验室井架钢结构加速度响应信号如图7所示,波形趋势相同。同样利用瞬态动力学分析对其他节点进行求解,可得到有限元模型编号1～20的节点加速度数据信息,与示例点波形趋势相同。

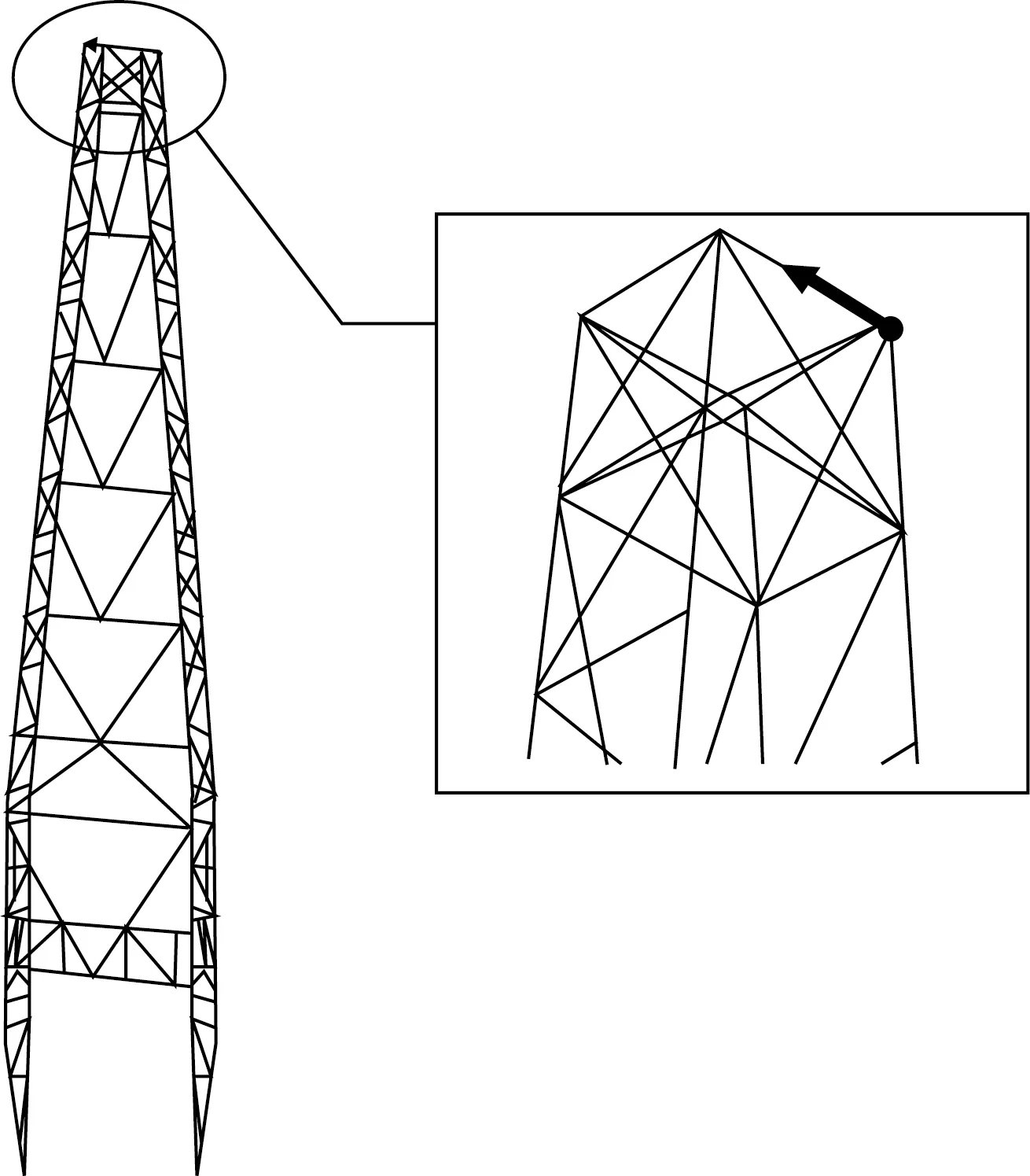
图5 冲击载荷施加位置、方向示意图Fig.5 Schematic diagram of impact load application position and direction

图6 井架钢结构有限元模型3号节点加速度响应信号Fig.6 Acceleration response signal of node 3 of the finite element model of the steel structure of the derrick

图7 实验室井架钢结构对应节点加速度响应信号Fig.7 Acceleration response signals of nodes corresponding to steel structures of laboratory derricks

2.2 提取多个时域特征

以3号节点为例,对提取的加速度响应信号进行时域特征提取,提取的时域特征分别为脉冲因子F1、裕度因子F2、峭度F3。

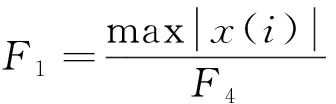
(8)

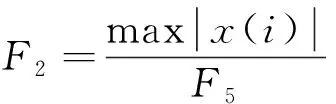
(9)

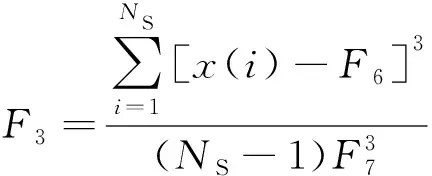
(10)

式中:x(i)为i时刻的加速度;F4为方根幅值;F5为有效值;NS为该时间段内数据的数目;F6为平均值;F7为标准差。

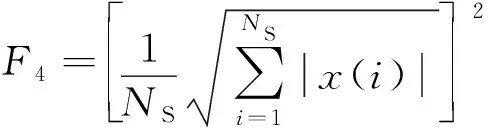
(11)

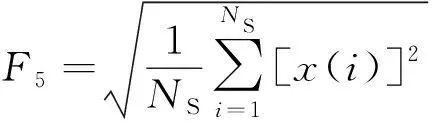
(12)

(13)

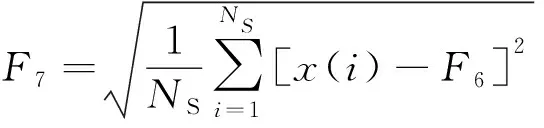
(14)

采用主成分分析法(PCA)对提取的时域特征进行处理,使多个特征融合成为一个新的包含大量信息的综合性特征,无损伤状态下各节点得到的综合性特征如图8所示。同理,可获得各种损伤状况下的综合性特征作为支持向量机方法的输入量进行井架钢结构的损伤识别。

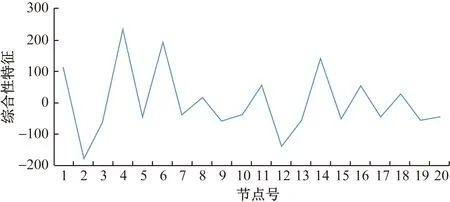
图8 无损伤状态下各节点综合性特征Fig.8 Comprehensive characteristics of each node in a non-damaged state

3 井架钢结构仿真算例分析

3.1 损伤工况设计

选取编号1～3处单元为研究对象,分别研究了不同位置单一损伤和多处损伤的情况。

损伤主要通过降低损伤单元的结构刚度来进行设计,设置以当量损伤系数为标准的不同损伤程度体现井架钢结构的多种损伤形式[19],每种损伤位置都包含10%、15%、17%、20%、25%、30% 6种损伤程度来对应实验和实际工作过程中可能会出现的各种程度的损伤,井架钢结构单一损伤工况如表2所示,井架钢结构多处损伤工况如表3所示,各种工况分别代表在不同损伤位置情况下,井架钢结构在冲击载荷下的工作状况。

表2 井架钢结构单一损伤工况Table 2 Single damage condition of derrick steel structure

表3 井架钢结构多处损伤工况Table 3 Multiple damage conditions of derrick steel structure

3.2 识别损伤位置

在同一工况下分别进行不同损伤程度和不同冲击载荷大小的多次仿真模拟,提取每次模拟时节点1～节点20的加速度响应信号应用主成分分析法进行计算,得出综合性特征。井架钢结构单一损伤时共进行209次模拟,井架钢结构多处损伤时共进行198次模拟。

为保证损伤识别的准确性和普适性采用随机抽取的方法确定输入支持向量机模型的训练集和测试集数据。井架钢结构单一损伤工况中随机抽取174组数据作为训练集,35组数据作为测试集;井架钢结构多处损伤工况中随机抽取148组数据作为训练集,50组数据作为测试集。

3.3 识别结果评估

将训练集和测试集数据输入支持向量机模型中,井架钢结构单一损伤工况下的训练集和测试集的识别结果分别如图9(a)和图9(b)所示,测试集识别率94.28%,历时约1.4 s。井架钢结构多处损伤工况下的训练集和测试集的识别结果分别如图10(a)和图10(b)所示,测试集识别率100%,历时约1.2 s。单一损伤和多处损伤工况下的损伤情况和损伤识别为独立的,识别结果互不产生影响,不存在相关性。通过图9、图10可直观看出识别过程中模型的识别结果和对应的正确结果。

图9 井架钢结构单处损伤识别结果图Fig.9 Single damage identification results of derrick steel structure

图10 井架钢结构多处损伤识别结果图Fig.10 Multiple damage identification results of derrick steel structure

由图9、图10中数据可知,该方法在井架钢结构损伤识别中有较高的可行性,在井架钢结构多处损伤工况识别的过程中识别率高达100%,可能存在的问题为:在仿真模拟的过程中各种条件都处于理想状态,且没有噪声干扰。所以需要进一步验证在实验室条件下该方法是否同样可行。

4 井架钢结构实验室模型验证

以1∶18的比例建立ZJ70井架钢结构实验室实物模型,井架钢结构实验室模型高度为2.95 m,整体材料为Q235钢,其属性如表1所示,各部分以销钉连接,利用模型连接处模拟井架钢结构的销钉和斜撑的损伤,利用8个加速度传感器采集井架钢结构不同位置在受到冲击载荷时振动产生的加速度响应信号。井架钢结构实验室模型、传感器布置及损伤位置设计如图11所示,图11拍摄于实验室。

图11 传感器布置、损伤设置图Fig.11 Sensor layout and damage setting diagram

传感器布置过程中虽不均匀,但完整覆盖实验所需验证的范围,能够全面地收集到必要的响应信号,保证了损伤识别结果的正确性,传感器由上到下依次编号1～8号。在损伤形式设置时,编号1～3处为销钉损伤形式,编号4～6处为斜撑损伤形式。在井架钢结构实验室模型的试验过程中模型单一损伤工况设计和多处损伤工况设计分别如表4、表5所示。

表4 井架钢结构实验室模型单一损伤工况Table 4 Single damage condition of laboratory model of derrick steel structure

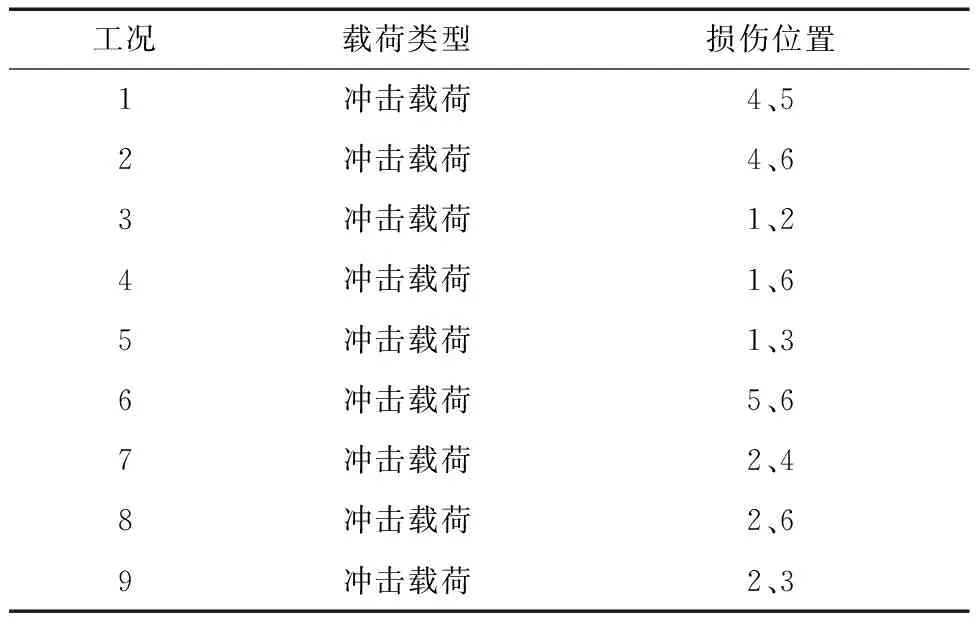
表5 井架钢结构实验室模型多处损伤工况Table 5 Multiple damage conditions of laboratory model of derrick steel structure

实验过程中在实验室井架钢结构模型顶部以橡胶锤敲击作为冲击激励,根据加速度传感器采集到的加速度响应信号提取脉冲因子、裕度因子和峭度的时域特征,利用主成分分析法融合形成每次实验各传感器处的综合性特征,将该综合性特征作为支持向量机模型的输入信号。井架钢结构实验室模型单一损伤工况下随机抽取230组数据作为训练集,75组数据作为测试集,井架钢结构实验室模型多处损伤工况下随机抽取390组数据作为训练集,130组数据作为测试集分别进行损伤识别。井架钢结构实验室模型单一损伤工况下测试集的识别结果和识别过程中的混淆矩阵分别如图12(a)、图12(b)所示,测试集识别率92%;井架钢结构实验室模型多处损伤工况下测试集的识别结果识别过程中的混淆矩阵分别如图13(a)、图13(b)所示,测试集识别率97.69%。通过混交矩阵又可以直接看出在识别过程中每类损伤工况下识别正确或错误的次数。

图12 井架钢结构实验室模型单处损伤识别结果Fig.12 Single damage identification results of laboratory model of derrick steel structure

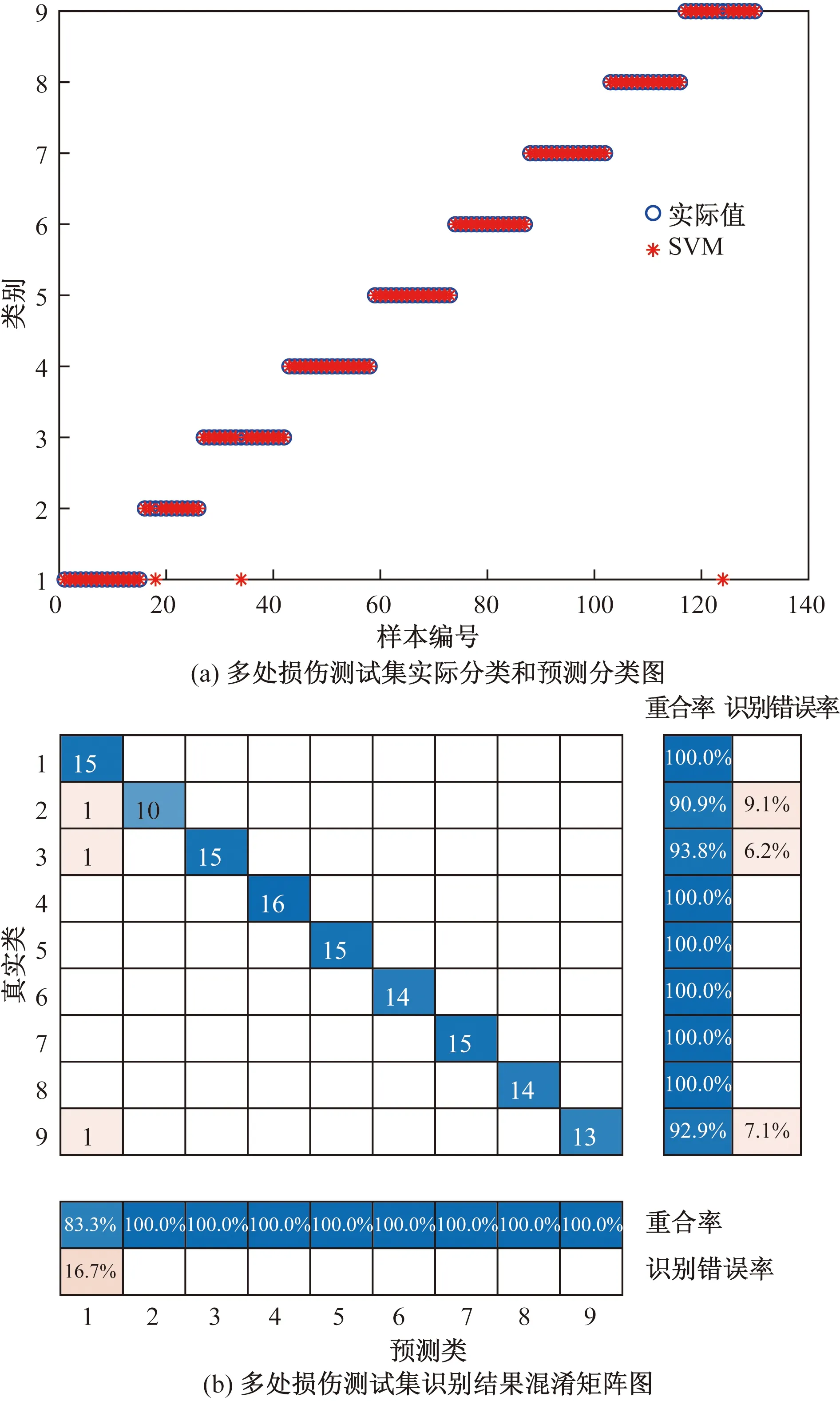
图13 井架钢结构实验室模型多处损伤识别结果Fig.13 Multiple damage identification results of laboratory model of derrick steel structure

通过利用井架钢结构实验室模型进行实验验证了PCA-SVM在对井架钢结构进行损伤识别时的有效性,因此该方法能够准确地识别不同工况下石油井架不同位置单一损伤或多处损伤的情况。

5 结论

仅利用井架钢结构的加速度响应信号,将主成分分析法与支持向量机模型结合起来创新的应用到了井架钢结构的损伤识别工作中,提出了基于PCA-SVM的井架钢结构损伤识别方法。

(1)利用主成分分析法能够将加速度响应信号的多个时频特征中尽可能多的信息融合到一起,形成一个新的综合性特征,有助于后续支持向量机模型对损伤位置的准确识别,并且压缩了数据集规模,大大提高了识别效率。

(2)通过对井架钢结构实验室模型进行实验,验证了在普通环境中PCA-SVM方法对井架钢结构损伤识别的准确性和适应性,所形成的结果图也较为直观易懂。

(3)PCA-SVM井架钢结构损伤识别方法只需要提取单一类型传感器的响应信号,且无需提取损伤前的数据,对设备和操作的要求较低,且识别时间较短,具有方便快捷的优点。