孤立波作用下振荡水柱波能转换装置的越浪研究

牟迪, 王荣泉, 宁德志, 陈丽芬

(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)

海啸常指地球地壳运动引起的海浪。通常引起海啸的原因包括但不限于:地震、风暴潮、水下爆炸等。当以上事件发生时,水面的突然抬升或者降低将产生沿各个方向传播的波浪,并产生海啸。结构物在海啸波作用下遭受猛烈的极端载荷并引起流体诸多强非线性现象。全球在过去的100年中,每年大约发生一次毁灭性海啸,在世界范围内造成严重的人员损失与财产破坏[1]。海啸在产生时,波幅较小,通常仅有1～2 m,但与当地水深相比,波长很长,通常在100 km左右。孤立波只有一个较大的波峰或波谷,其波形和水质点的运动与海啸极为相似,因此常被用来模拟海啸等浅水大波[2]。

从大量海洋灾害所造成破坏的案例看来,海啸引发的越浪现象,是造成海洋结构物破坏及财产损失的重要原因之一。自20世纪起,国内外众多学者已经对于越浪问题进行了大量的研究并取得了大量研究成果[3-5],但以往的研究多集中于海啸波与不同结构形式的海堤或者近岸跨海桥梁等海岸结构物作用时产生的越浪现象,而关于孤立波与振荡水柱式(oscillation water column, OWC)波浪能转换装置作用下引起的越浪现象研究较少。

OWC波能装置的主体带有一个下端开口的气室结构,气室上部有通气管道连接空气透平。在波浪作用下,水柱上下振荡迫使气室内部空气在通气管道处形成往复气流,气流通过推动空气透平带动发电机工作产生电能。其与普通海洋结构物不同之处主要在于结构内部气室的存在,气室内部上方气流由于气孔的阻碍作用使气压增大,进而抑制气室内部自由液面的上升。被抑制的水柱通过压强的传递进而影响波浪在前墙上的爬坡运动最终对越浪产生影响。以往对该装置的研究多从水动力转换效率角度出发,优化该装置结构,提升其波能转换能力[6-8]。而对于该装置在极端波况下的水动力特性,国内外大多学者关注点集中在装置的受力情况,如马子然[9]研究了在聚焦波作用下,离岸式OWC装置的受力情况。尽管如此,目前未见有关于极端波浪作用下,OWC波能装置越浪特性的研究。

所以本文基于以上背景,利用开源软件OpenFOAM 中waveIsoFoam求解器求解三维Navier-Stokes方程,对孤立波与OWC装置作用时发生的越浪现象进行数值模拟研究,分析与越浪相关的物理量如越浪量、越浪厚度、越浪流速度等随相对波高改变的变化规律,并展示越浪发生时的流场特性。为OWC波能装置的优化及安全设计提供理论指导。

1 数学模型

1.1 控制方程

本文假定流体不可压,无热传导。基于上述假定,N-S方程可分为连续性方程及动量方程:

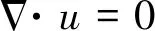
(1)

(2)

式中ρ、μ表示混合流体密度及流体粘度。u=(u,v,w)和x=(x,y,z)为笛卡尔坐标系下流体速度矢量与位置坐标,p*为动压,g为重力加速度。

1.2 自由液面捕捉

本文通过VOF方法获得自由液面运动。该方法求解运输方程(3)以获得体积分数:

(3)

式中:α为每个网格体心的体积分数,如果α的值界于0～1,则这个网格则被标记为包含自由液面的计算网格。当α=0时,对应为气相;当α=1时,对应水相。单元内流体物理属性为:

(4)

式中:角标a与w分别代表空气与水,尽管基于不可压缩假定,但是交界面处密度随计算时间步推进而时刻变化。

在本文中,用于重构自由液面的VOF方法为Iso-advector 方法,该方法是一种基于几何特征的重构方法。相比于基于代数重构的MULES方法,该方法在计算效率、收敛性、稳定性有着较强的优势,关于该方法详细描述见文献[10-11]。

1.3 孤立波方程

本文采用waves2Foam中提供的一阶孤立波波面方程进行数值造波,并在计算域两侧分别布置被动消波区域。其中孤立波波面方程为:

(5)

(6)

(7)

(8)

式中:η为孤立波波面;H为孤立波波高;d为水深;c为孤立波波速。

1.4 离散格式及边界条件

本文采用有限体积法将计算域离散成众多结构化网格。对于方程(2)中时间项采用一阶Euler隐式离散,对流项采用linearUpwind 二阶TVD格式离散,在保证计算精度的同时保证其求解的稳定性,速度梯度通过Gauss linear interpolation 方法进行插值计算。速度压力耦合通过pimple算法求解,pimple算法为simple算法与piso算法的结合,允许用户根据所设定的最大库郎数进行时间步的自适应调节[12],本文计算中库郎数为0.3。

本文中所采用的边界条件如下:对于所有结构物物面及底部地面,采用noslip无滑移边界条件并配合zeroGradient 零梯度压力边界条件;对于计算域顶部采用totalPressure及pressureInletOutlet边界,即在顶部指定总压,并仅允许空气流出,不允许回流。

2 模型验证

2.1 网格收敛性验证

为排除空间离散对数值结果产生的影响,本节将进行网格收敛性验证。表1列出了不同网格参数,结构物外部水平方向网格与垂向网格尺寸相等。由于气孔处通量变化较大,对其附近区域进行了局部加密(见图1)。数值模型中计算域尺寸与物模实验中保持一致(见下节)。图2展示了不同网格下由OpenFOAM模拟得到的x=9.3 m处波面历程,本文模拟中水深保持d=0.4 m。图2中,不同网格得到的结果差距较小,为平衡数值结果与计算量,最终选择中等程度的网格进行计算。

表1 网格尺度

图1 网格示意

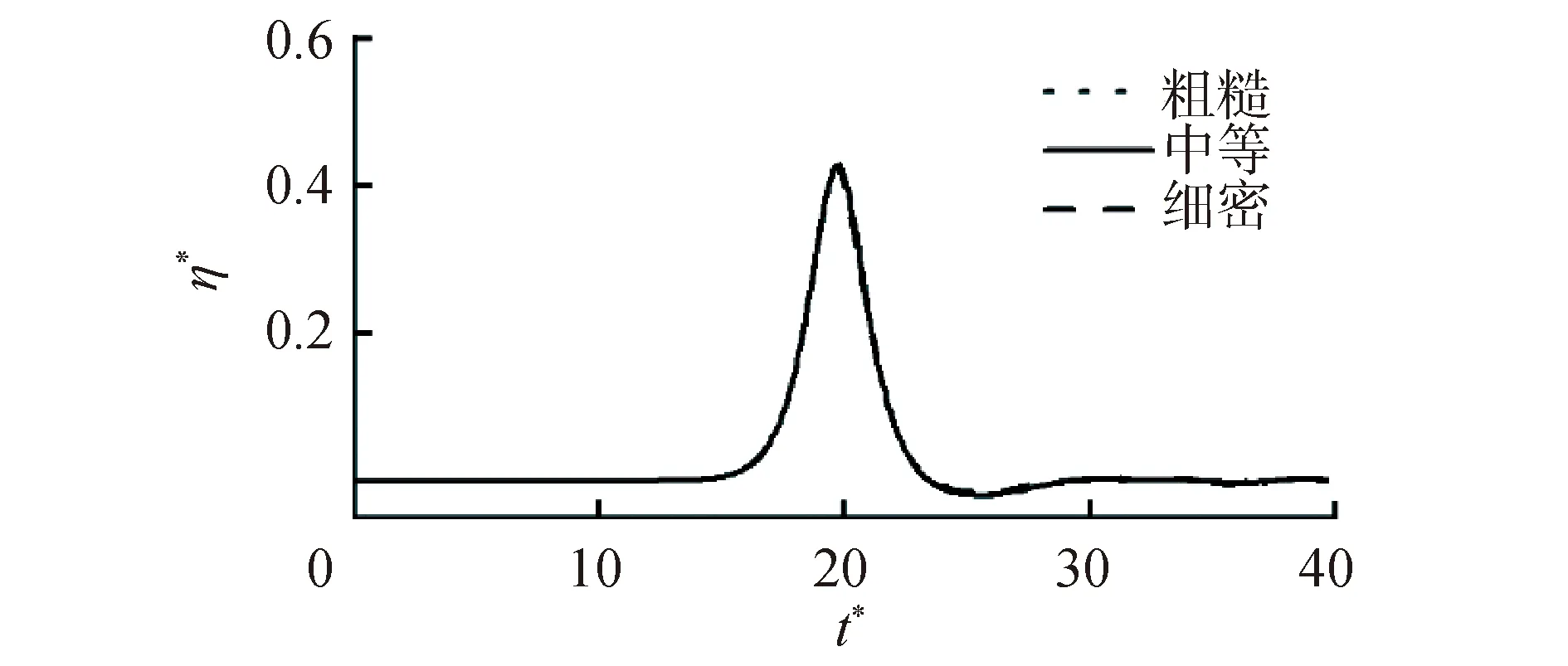
图2 H*=H/d=0.425时不同网格下波面历程(η*=η/d,t*=t(g/d)1/2)

2.2 模型验证

试验在大连理工大学海岸及近海工程实验室PIV水槽进行,水槽长22 m、宽0.45 m、高0.6 m。如图3所示,模型由厚度为0.012 m的有机玻璃制成,装置前墙固定于距造波板9.3 m处,以保证孤立波在传播过程进行充分演化。装置的具体几何尺寸见表2。由于水槽宽度较小,并且在孤立波作用时,自由液面伴随着强非线性破碎现象,难以准确测量距前墙较近处自由液面变化,故无接触式超声波浪高仪安置在距装置前墙2.6 m处。为避免测力计应变片微小运动而引起受力的不准确测量,2个测力计分别安装于装置顶部与后方底部并通过一钢架固定于水槽侧壁。实验结果表明,通过双测力计测量得到的总力,其结果误差小于3%。

表2 结构物尺寸

图3 本次实验示意

图4分别展示数值模拟结果与模型实验结果的对比。

图4(a)第1个峰值为入射波,第2个峰值为反射波。OpenFOAM计算得到的反射波峰值略大于实验结果,其原因为实验水槽侧壁高度受限,波浪与前墙作用时部分水体由水槽两侧溢出而导致能量部分损失,最终使反射波波高有所降低。图4(b)展示气室内气压对比,其中正压对应于OWC运动的上升阶段,当气室内液面高度达到最大时,气室内气压降至零。此后,OWC开始做下降运动,气室内部产生负压,外部空气被吸入至气室内部。图4(c)展示结构总水平力对比,受力曲线呈现单峰状,受力峰值与实验结果误差小于2%。总体来说,数值模拟结果与实验结果对比良好,验证了OpenFOAM模型的有效性。

3 结果与讨论

3.1 越浪量变化规律

采用Baldock等[13]提出的方法,选取孤立波在静水面以上的单宽水体体积作为特征量定义无量纲越浪量即:

q*=q/q0

式中:q为数值模拟得到的单宽越浪量;q0为孤立波在静水面以上的单宽水体体积,对方程(5)积分可得:

(9)

图5给出无量纲越浪量与相对波高的关系,所监测断面为前墙上方,其中定义相对波高H*=H/d。可以看出越浪量随相对波高增大而明显增大,曲线呈现出线性变化趋势,该结果与Baldock等[13]、张金牛等[14]实验所测孤立波与防波堤作用所得越浪量的变化规律类似。对比数值结果与不同经验公式,可以看出,3种结果虽然趋势保持一致,但越浪量大小有着明显区别,Baldock等[13]所提出的经验公式是基于孤立波与缓坡作用模型,而张金牛等[14]则通过模型实验提出了适用于孤立波与陡坡模型作用的经验公式,因此Baldock等[13]公式所得结果最大。相比于以上结果,本文的OWC模型更类似于以上适用条件的极限情况,因此所得结果最小。

图5 相对波高对越浪量影响(H*=H/d,q*=q/q0)

3.2 越浪厚度沿程变化规律

图6(a) 给出无量纲越浪厚度沿程衰减规律,其中,C0为OWC前墙上方越浪流厚度;Ci为OWC上顶板任意位置处的越浪流厚度;xi为上顶板任意位置距OWC前墙距离;以顺流方向为正。从图7中可以看出,除x*≈1.1处外,越浪流厚度均沿程变小,衰减系数随相对波高增大而增大,且在上顶板前半部分衰减速度大于后半部分。孤立波与OWC作用时,先沿前墙进行爬坡,靠近前墙附近的水体仅有垂直方向流速,但随着爬坡水体厚度增加,部分水体由于左侧水体作用仍具有部分水平速度(见4.4节),因而,越浪水体沿一角度入射至OWC上顶板,在上顶板底部形成一密闭空腔。由于空腔无法从两侧排出,随越浪流逐渐顺流运动,在x*≈1.1处破碎释放,所以引起水体厚度局部增大。尽管存在OWC气室的非线性作用,但本文所得结果趋势与Oumeraci等[15]提出的规则波与防波堤作用下的越浪厚度衰减经验公式趋势保持一致(图6(b)),但对比张金牛[14]针对于孤立波越浪提出的改进经验公式,在堤顶后方与本文模拟结果具有较大差别,可能是由于实验中防波堤后方水流较浅,难以准确测量导致。

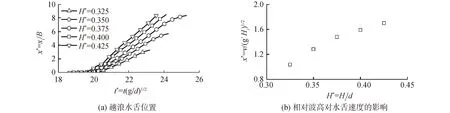
图7 越浪流传播情况

3.3 越浪流传播速度

越浪现象发生时,越浪流在结构物顶部传播的速度称为越浪流速度(水舌速度),越浪流速度大小将间接影响岸边结构物所受到的越浪冲击力。图7展示越浪水舌位置的时间历程,及越浪流速度随相对波高改变的变化规律。在越浪流传播后期,其主要受到底部切应力影响,最终自由液面会产生不连续现象,故图7(a)中水舌位置仅选取连续的水面过程。由图7中可以看出,在整个时间历程中,越浪流主要以匀速传播。图中在初始阶段有一明显的速度转折,原因与上节类似(越浪流呈一角度入射至上顶板)。越浪流传播速度通过匀速运动过程中位移曲线斜率获得。图7(b)给出该速度随相对波高变化关系,发现随相对波高增大越浪流传播速度增大,且在相对波高为0.375时存在一微小转折,此后速度增大程度稍有变缓的趋势。

3.4 越浪水体形态及砰击现象

借鉴Oumeraci等[15]研究越浪时把越浪划分成若干个阶段的方法,本文将整个过程划分为4个特征阶段。云图中,箭头仅代表流动方向,流速大小由云图颜色表示。

1)波浪到达前墙并与前墙作用产生变形,水体沿前墙继续爬升,由于前墙不透水,紧贴前墙一侧水体仅有垂直方向流速,而外侧水体仍带有部分水平速度分量(图8(a))。

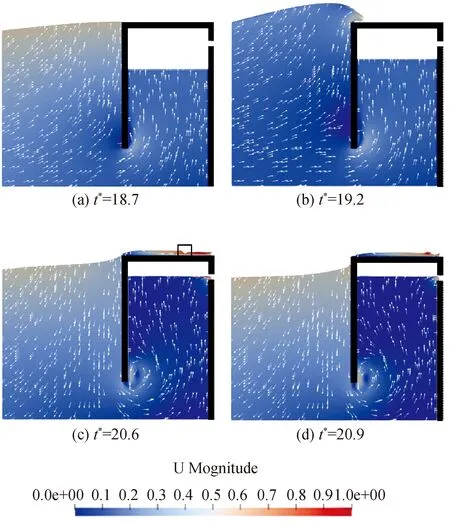
图8 越浪流场

2)波浪越过前墙,失去前墙作用的水体由于惯性继续向斜上方运动,最终受到重力作用产生回落,回落的水舌以一角度入射至上顶板,在与上顶板作用瞬间产生了较为明显的砰击现象,引起局部受力增大(图8(b))。

3)在砰击作用发生的瞬间,由于存在入射角度,小部分空气被卷入并由水体包裹随越浪流的演化顺流运动(图8(c) 方框线),此时随着越浪厚度逐渐减小,该空腔逐步被释放。当空腔经过采集位置时,造成瞬时越浪量减小与越浪厚度的突变。

4)随着越浪的继续进行,左侧波浪开始后退,波浪不再向上顶板输送水体,越浪流左侧动压降低,由于上顶板仍有水体存在,阻碍了水体继续向前流动,故在重力作用下,部分水体从左侧回流,此时出现了顶板后方水体厚度大于前方的情况(图8(d))。

图9展示上顶板在不同相对波高作用下,各测点波压力的极值沿水平位置的变化情况。由图9中可以看出,波压力极值随相对波高增大而明显减小,不同相对波高下,顶板波压力极值存在一个突变点,突变点处波压力明显增大并且随相对波高增大,突变量变大,作用位置逐渐向后方移动,突变点位置对应于砰击现象所发生的位置,即砰击点。根据Li[16]所述,越浪流在与前墙作用后,与上顶板作用前,垂直方向作自由落体运动,水平方向做匀速运动。由于初始入射速度随相对波高增加而增加,进而导致回落时间增加,所以当发生越浪现象时,水舌在空中水平运动距离变大,最终导致砰击点逐渐向后方移动。

4 结论

1)以往基于规则波或不规则波与防波堤作用模型所提出的越浪量经验公式与如今的数值模拟结果趋势相同,即越浪量均随相对波高的增大而线性增大,但其结果明显偏大,因此不适用于OWC模型。

2)越浪厚度与经验公式对比良好,随相对波高增大而增大,因此OWC气室的存在对越浪厚度影响较小。越浪流在顶部传播时以匀速阶段为主,该速度随相对波高增大而增加。

3)通过流场分析发现,在越浪现象发生的同时,由于越浪流沿一角度与上顶板作用,导致了顶板砰击现象的发生。砰击压强随相对波高增大而降低,砰击点也随之后移。因此需要在设计时考虑采取相应措施减小该砰击现象所带来的危害。

本文以期为振荡水柱波能转换装置的优化及安全设计提供理论指导。