基于补偿函数观测器的无人机吊挂飞行控制

刘肩山 唐毅 谢志明

摘  要：无人机吊挂飞行系统是多变量、欠驱动、强耦合的非线性系统，且该系统存在模型偏差和未知扰动，给无人机位置和吊挂飞行减摆控制带来了困难。文章设计了一种基于补偿函数观测器（CFO）的非线性控制方法。首先，基于拉格朗日方程建立系统的动力学模型。然后，设计了补偿函数观测器来估计未建模动态和扰动，并将估计值反馈给控制器以大幅减弱其给吊挂飞行减摆控制带来的不利影响。仿真实验对比了线性自抗扰控制（LADRC）以及线性二次型调节器（LQR）两种控制方法，结果表明设计的控制器抗扰性更好、鲁棒性更强、控制精度更高。

关键词：外界干扰；补偿函数观测器；障碍Lyapunov函数；反步控制器；减摆控制

中图分类号：TP273.1   文献标识码：A   文章编号：2096-4706（2023）16-0062-05

Control of Unmanned Aerial Vehicle with a Slung-load Based on

Compensation Function Observer

LIU Jianshan， TANG Yi， XIE Zhiming

（Changsha Aeronautical Vocational and Technical College， Changsha  410124， China）

Abstract： Unmanned Aerial Vehicle with a slung-load flight system is a multi-variable， underactuated and strong coupling nonlinear system， and the system has model bias and wind disturbance which increase the difficulty of UAV position and anti-swing control of slung-load flight. This paper designs a nonlinear control method based on CFO. Firstly， the system dynamic model is built by using Lagrangian mechanics equation. Then， a CFO is designed to estimate the unmodelled dynamics and disturbances， and the estimated values are feed back to the controller to greatly reduce its adverse effects on the slung-load flight anti-swing control. The simulation experiment compares the two control methods of LADRC and LQR， and results show that the designed controller has better disturbance immunity， stronger robustness and higher control precision.

Keywords： external disturbance; Compensation Function Observer; barrier Lyapunov function; backstepping controller; anti-swing control

0  引  言

四旋翼無人机吊挂飞行因其具有无须考虑吊挂负载外形影响、不受地理条件限制、效率高、成本低、操作灵活等优点，在军用和民用的各个领域得到应用，如物资运输、抢险救灾、水质监测取样、雷区探测扫描等[1，2]。四旋翼吊挂无人机是一个多变量、非线性、欠驱动、强耦合以及时变的系统，在实际飞行中，系统稳定性会受到负载摆动的影响，且存在系统参数变化、外界干扰、模型不精确等问题，使无人机吊挂飞行控制变得复杂。因此，为了扩展其应用范围，设计具有高抗扰能力的控制器就显得十分有必要，也成为近年来研究的热点和难点。

由于吊挂负载并不能给系统增加控制输入，四旋翼无人机吊挂系统是欠驱动的，对该系统的建模主要使用欧拉—拉格朗日方程[3]，该方法基于能量平衡原理，不需要求解吊挂系绳上的作用力。文献[4，5]在建模过程中考虑了更多的细节，如系绳的弹性、有无张力、以及负载空气动力学对无人机飞行控制的影响。Lee将无人机吊挂系统控制输入分解为机体系的垂直分量和水平分量，在水平分量上采用反馈线性化控制[6]，不过该方法控制效果取决于系统模型是否精确。文献[7]针对负载轨迹跟踪控制，基于反步法设计了Lyapunov函数，证明了闭环系统的渐近稳定性，实际的飞行实验也验证了无人机吊挂系统所有状态的一致有界。文献[8]采用分层滑模控制方法来解决控制变量耦合问题，并利用吊挂刀锯摆角信息设计了无人机位置和负载摆角综合控制器。

无人机吊挂系统需要考虑建模不精确、参数摄动和外扰对飞行控制的影响，为提高系统的动态性能和鲁棒性，文献[9]提出将被控对象存在的耦合、内扰和外扰等直接视为总扰动，设计扩张观测器（ESO）估计总扰动。文献[10]提出了补偿函数观测器，通过添加补偿函数来抵消未知函数对估计精度的影响，能高精度估计未建模动态和扰动。

本文基于拉格朗日方程建立了四旋翼无人机吊挂系统动力学模型，考虑到强耦合、空气阻力、未建模动态和风扰等因素对飞行控制的影响，将无人机的位置和负载摆角综合为一个控制向量，对被控变量进行同频率控制；设计CFO对扰动和模型偏差进行估计，并将估计值反馈给比例微分控制器，提高了系统的准确性和稳定性；最后，将本文设计的控制算法与基于LADRC和LQR的控制算法进行了比较，结果表明本文设计的控制算法具有更好的控制效果。

1  系统模型分析

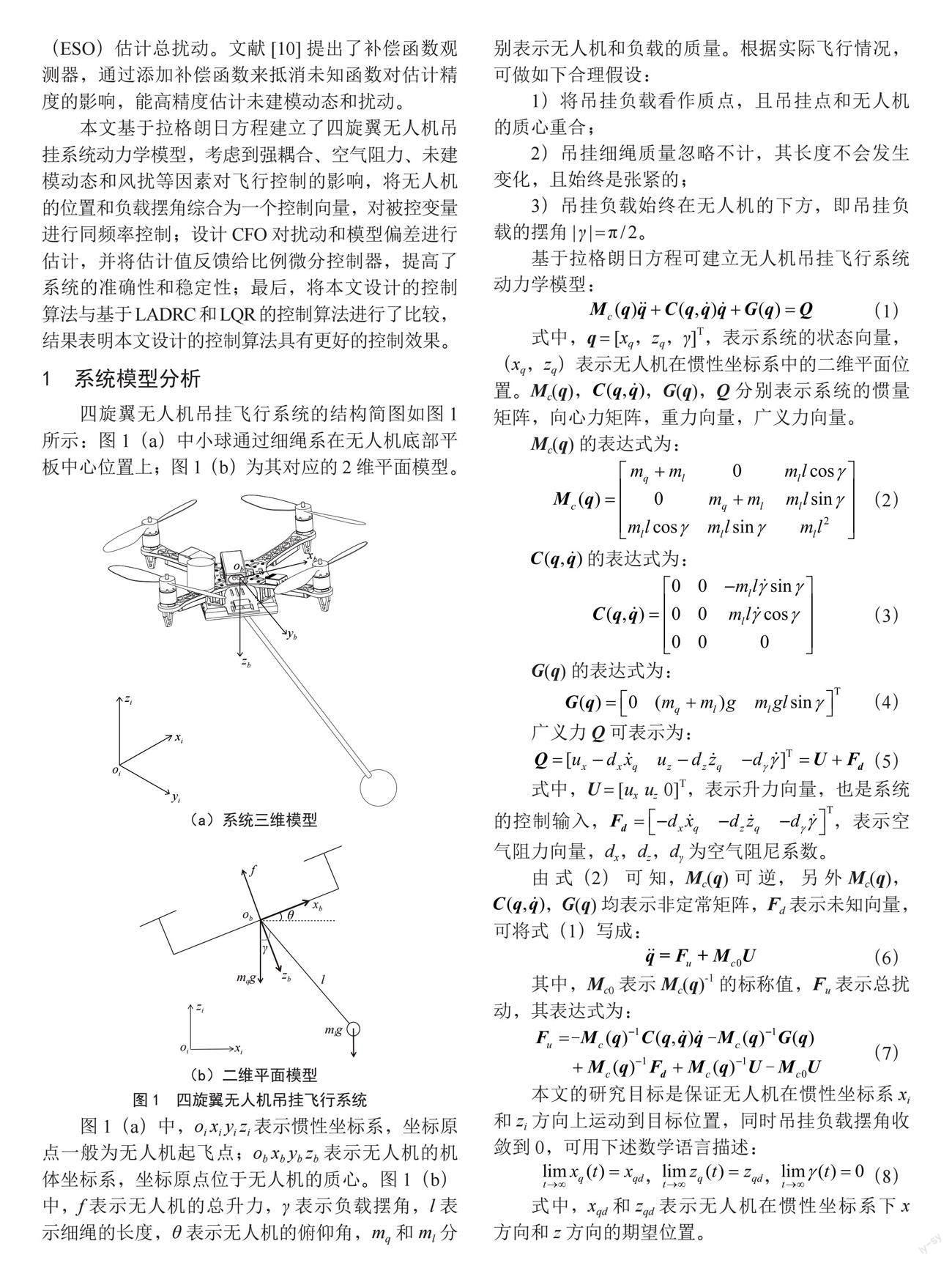
四旋翼无人机吊挂飞行系统的结构简图如图1所示：图1（a）中小球通过细绳系在无人机底部平板中心位置上；图1（b）为其对应的2维平面模型。

图1（a）中，oi xi yi zi 表示惯性坐标系，坐标原点一般为无人机起飞点；ob xb yb zb表示无人机的机体坐标系，坐标原点位于无人机的质心。图1（b）中，f表示无人机的总升力，γ表示负载摆角，l表示细绳的长度，θ表示无人机的俯仰角，mq和ml分别表示无人机和负载的质量。根据实际飞行情况，可做如下合理假设：

1）将吊挂负载看作质点，且吊挂点和无人机的质心重合；

2）吊挂细绳质量忽略不计，其长度不会发生变化，且始终是张紧的；

3）吊挂负载始终在无人机的下方，即吊挂负载的摆角| γ | = π / 2。

基于拉格朗日方程可建立无人机吊挂飞行系统动力学模型：

（1）

式中，q = [xq，zq，γ]T，表示系统的状态向量，（xq，zq）表示无人机在惯性坐标系中的二维平面位置。Mc（q），，G（q），Q分别表示系统的惯量矩阵，向心力矩阵，重力向量，广义力向量。

Mc（q）的表达式为：

（2）

的表达式为：

（3）

G（q）的表达式为：

（4）

广义力Q可表示为：

（5）

式中，U = [ux uz 0]T，表示升力向量，也是系统的控制输入，，表示空气阻力向量，dx，dz，dγ为空气阻尼系数。

由式（2）可知，Mc（q）可逆，另外Mc（q），，G（q）均表示非定常矩阵，Fd表示未知向量，可将式（1）写成：

（6）

其中，Mc0表示Mc（q）-1的标称值，Fu表示总扰

动，其表达式为：

（7）

本文的研究目标是保证无人机在惯性坐标系xi和zi方向上运动到目标位置，同时吊挂负载摆角收敛到0，可用下述数学语言描述：

，，（8）

式中，xqd和zqd表示无人机在惯性坐标系下x方向和z方向的期望位置。

2  控制器设计

2.1  补偿函数观测器

CFO比ESO多使用了狀态向量的微分信息，且通过对状态向量误差及其微分进行积分来补偿未知模型函数项Fu的影响。CFO比ESO高两个型别，为Ⅲ型系统，其精确度和收敛性都要优于ESO。另外，CFO是指数收敛的，在Fu为三阶无穷小函数向量的条件下，其扩张状态向量能以零稳态误差收敛到Fu。由式（6）可得系统的状态方程：

（9）

其中，x1 = q，U表示控制输入向量。由式（9）可得CFO表达式：

（10）

其中， 表示对q的估计值， 表示对总扰动Fu的估计值， 表示误差矩阵，λ表示滤波参数矩阵，L = [l1，l2]表示增益矩阵，l1，l2，λ均表示三阶对角矩阵，其表达式如下：

，，（11）

式中，l1i，l2i，λi（i = x，z，γ）满足如下特征方程：

s3 + l1i s2 + （ λi l1i + l2i ） s + λi l2i = 0        （12）

配置观测器的极点为s1 = -wi，s2， 3 = -4wi，有l1i = 9wi，l2i = 12wi2，λi = 4 / 3 wi，wi表示通道的带宽。

2.2  控制器设计

通过CFO对系统的观测，可以得到总扰动估计值 ，结合总扰动主动补偿和跟踪误差比例微分反馈的控制律设计如下：

（13）

其中，qd = [xqd，zqd，γqd]T表示无人机位置x、位置z和吊挂负载摆角γ的期望值组成的列向量，KP和Kd的表达式如下：

，（14）

式中，ωcx、ωcz和ωcγ分别表示控制器在位置x，位置z和摆角γ通道的带宽。

3  仿真实验

为验证设计的控制器对无人机吊挂飞行系统的控制效果，在[10，20] s将如图2所示的风扰注入系统的x通道和z通道，在仿真的第30 s至35 s模拟了吊挂负载质量持续减少一半的控制效果，并通过与LADRC和LQR控制方法进行对比，以验证所提算法的有效性及优越性。四旋翼无人机吊挂系统的参数为：mq = 1.008 2 kg，ml = 0.076 kg，l = 1.085 m，g = 9.81 m/s2。设定吊挂飞行系统的初始位置为：xq0 = 0 m、zq0 = 1.5 m，目标位置为：xqd = -1.5 m、zqd = 3 m。

本文设计的CFO的相关参数为：wx = 6，wz = 6，wγ = 6，用于对比的ESO的相关参数为：ωox = 80，ωoz = 80，ωoγ = 500，ωox、ωoz和ωoγ分别表示ESO在位置x、位置z和摆角γ通道的带宽。

为了对比CFO和ESO的收敛性和精度，本文设计的比例微分控制器和自抗扰控制器相关参数均为：ωcx = 1.5，ωcz = 1.5，ωcγ = 0.2，ωcx、ωcz和ωcγ分别表示控制器在位置x，位置z和摆角γ通道的带宽。用于对比的LQR控制器参数是通过对系统在平衡点处进行线性化处理后借助MATLAB中Simulink的Linear Analysis Tool求得。

图3描述了CFO-PD、LADRC和LQR三种控制方法下无人机位置及负载摆角随时间变化的情况。由图3可知，LQR方法在无人机位置跟踪方面和吊挂负载的减摆控制方面表现不佳，需要超过5 s的时间才能完成位置指令的零稳态误差跟踪，并且在无人机飞往目标位置过程中，负载摆角有明显的振荡。而CFO-PD和LADRC方法在位置跟踪和负载减摆控制方面性能接近，在无人机飞往目标点过程中，负载均无摆动，且CFO-PD在位置z通道跟踪快速性方面要优于LADRC方法。当飞行器受到风扰时，LQR方法下的位置通道和摆角通道都出现了较大幅度的振荡，抗干扰性能较差，其中吊挂负载的最大摆角甚至达到了13°，位置x通道的最大超调量为75%，位置z通道的最大超调量为80%；当扰动消失后，LQR需要4.5 s的调整时间以让稳态误差消失。采用LADRC和CFO-PD控制器的系统在受到风扰后，都表现出了良好的抗扰性能，无人机位置和摆角仅出现了很小幅度的波动，且在扰动消失后，很快就恢复到原来的状态，但是从图中可以看出，CFO-PD的鲁棒性要明显优于LADRC，位置和吊挂负载摆角几乎无任何波动，这是因为CFO是Ⅲ型系统，对扰动的估计精度更高。另外，当吊挂负载质量减少时，可以发现LQR方法不能保证位置z的跟踪，出现了0.4 m的稳态误差，而CFO-PD和LADRC方法几乎不受影响。

图4为三种控制方法下无人机的控制输入随时间变化情况，可以发现CFO-PD和LADRC方法均对控制指令在短时间做出了响应，而LQR方法响应较慢，而且控制输入相比CFO-PD和LADRC小得多。在风扰期间，CFO-PD和LADRC方法下的控制输入均能很好地根据外部扰动及时做出响应，能跟上风扰的变化，而LQR方法下的控制输入则有明显的滞后，且并不能快速跟上风扰的变化。在吊挂负载质量持续减少时，通过图4（b）中局部放大区域可以看到，CFO-PD方法下的控制输入响应最为迅速，LADRC次之，LQR则最慢。

综上，本文提出的CFO-BLF反步控制器能使无人机吊挂飞行系统快速、高精度飞往目标位置，且在飞行过程中能极大抑制吊挂负载的摆动，同时在对抗外部风扰和内扰方面具有极强的鲁棒性。

4  结  论

针对风扰和系统内扰下的无人机吊挂飞行系统减摆控制问题，本文通过对系统动力学模型分析得到系统状态方程，并设计了基于补偿函数观测器的非线性控制器。补偿函数观测器可以有效估计内扰和外界干扰，并将这些总扰动精确地补偿给PD控制器，抑制总扰动对系统带来的不利影响。仿真实验表明，本文设计的非线性控制器实现了无人机吊挂飞行系统的精确位置控制和吊挂负载的减摆控制，具有比LADRC和LQR控制器更快的跟踪速度、更强的鲁棒性和更高的跟踪精度。由于条件和时间有限，本文是从仿真的角度进行研究，下一步的工作将在实际系统中进行试验验证。

参考文献：

[1] 齐俊桐，平原.无人机吊挂飞行控制技术综述 [J].无人系统技术，2018，1（1）：83-90.

[2] 梁晓，胡欲立.四旋翼吊挂运输系统动态反馈线性化轨迹控制 [J].自动化学报，2020，46（9）：1993-2002.

[3] DE ANGELIS E L，GIULIETTI F，PIPELEERS G. Two-time-scale control of a multirotor aircraft for suspended load transportation [J].Aerospace Science and Technology，2019，84：193-203.

[4] SHIRANI B，NAJAFI M，IZADI I. Cooperative load transportation using multiple UAVs [J].Aerospace Science & Technology，2019，84（Jan）：158-169.

[5] KOTARU P，WU G，SREENATH K. Dynamics and control of a quadrotor with a payload suspended through an elastic cable [C]//2017 American Control Conference （ACC）.Windsor：IEEE，2017：1-4.

[6] LEE T. Geometric control of quadrotor UAVs transporting a cable-suspended rigid body [J].IEEE Transactions on Control Systems Technology，2017，26（1）：255-264.

[7] YU G，CABECINHAS D，CUNHA R，et al. Nonlinear backstepping control of a quadrotor-slung load system [J].IEEE/ASME Transactions on Mechatronics，2019，24（5）：2304-2315.

[8] 常樂.吊挂刀锯树障清理空中机器人控制技术研究 [D].南京：南京航空航天大学，2020.

[9] 高志强.自抗扰控制思想探究 [J].控制理论与应用，2013，30（12）：1498-1510.

[10] 齐国元，李阔，王琨.基于补偿函数观测器的四旋翼无人机姿态受限控制 [J].吉林大学学报：工学版，2023，53（3）：853-862.

作者简介：刘肩山（1989—），男，汉族，江西九江人，讲师，硕士研究生，研究方向：无人机非线性控制；唐毅（1979—），男，汉族，湖南长沙人，讲师，硕士研究生，研究方向：无人机飞控开发；谢志明（1981—），男，汉族，湖南株洲人，讲师，硕士研究生，研究方向：无人机应用与系统开发。