一种配网线损在线监测数据缺失自适应填补方法设计

曹 晶，谢文浩，周志飞，刘旭阳

（1.国网湖南省电力公司，长沙 410004；2.国网湖南供电服务中心（计量中心），长沙 410004）

配电网结构相对复杂，存在拓扑多变、监测难度大以及整定难度大的问题。随着配电网应用范围和用户数量不断上升，配网线损问题也越来越严重。配网线损在线监测数据缺失不仅会影响配电网的运行、调度、分析等工作，还对线路运行质量造成了一定程度的损害，导致配电网工作效率和质量有所下降。

在配网线损在线监测数据累积量较多的现状下，文献[1]提出基于次序依赖的配电网数据自动填补修复模型构建方法，但方法逐步查找计算的工作量较大，应用在实际电网线损检测中不易实现；文献[2]提出基于DBSCAN 二次聚类的配电网缺失数据填补方法，由于配电网中不只存在一种属性数据，是多种数据叠加，特征规律难以查找和捕捉，运用该方法进行数据缺失填补的误差较大。

结合上述分析，本文以配网线损的数据损失函数为基础，提出基于加权类平均的配网线损在线监测数据缺失自适应填补方法，并通过实验验证了该方法的有效性。

1 配网线损在线监测数据的聚类处理

本文采用聚类算法对配网线损全部数据进行聚类处理，具体操作步骤如下：

（1）将配电线路中特征表现最为明显的线损点作为数据样本X=｛x1，x2，…，xn｝（n 为样本数量），将样本数据的线损特征作为无量纲指标[3]，选用极值法对全部数据进行无量纲化处理。

（2）以步骤（1）预处理后的线损数据特征作为初始输入值，将样本集X 划分为c（c＞1）个类别，以此实现数据聚类。根据求得的每个样本的隶属度[4]uij值，计算其与聚类中心vi的距离，通过距离判定数据的所属类别范围。聚类目标函数JFCM为

（3）结合上述分析输出最终配网线损在线监测数据聚类结果。按照上述过程，通过初始数据输入求得配电线路中目标点距线损点的距离值，根据该距离值设定线损影响范围，可以为后续的数据缺失自适应调补奠定坚实的基础。

2 缺失数据区域定位

本文通过分析配网线损数据特征，建立损失函数[7]，通过损失函数尽可能找到缺失数据的真实区域，提高填补精准性。损失函数f（x）定义为

为了提升数据质量，需要保证配网线损缺失数据损失函数最小化，结果如下：

对于真实样本y 而言，要想提高配网线损计算的准确性，需要确保输出结果D（G（z））与期望结果之间的贴合度足够大，此时，线损计算结果才能不断逼近真实值。

将损失函数f（x）逼近问题转换为min-max 可得到：

由于配电网数据具有实时变化特性[10]，需要不断更新并输入特征计算，这样求得的损失结果才更贴近真实值，结合该结果进行缺失数据区域定位。

3 数据缺失自适应填补方法设计

在定位配网线损数据缺失数据区域后，计算不同数据之间的相似度[11]。通过相似度判定可大大降低多次查找效率，即可根据一组缺失数据的属性分析，查找与其存在正向关联的数据，提高配网线损在线监测数据缺失自适应填补效率[12]。

设An、Bn为同一聚类簇中的2 条缺失数据记录，其中αi、βi为数据i 的不同的属性值，将二者之间的损失量定义为

αi、βi的相似度定义为

式中：lmax表示数据i 属性相似性最大差异。通过式（8）可得到配网线损缺失数据的基本取值范围Si（αi，βi）为0～1 之间，查找损失量最大且与该样本相似性最高的数据点即可判定缺失点位置。

本文以缺失数据的属性特征、采样点数量以及缺失连续性为参照基础，采取针对性的填补策略。缺失数据采样点和连续性对配电网的影响如图1所示。

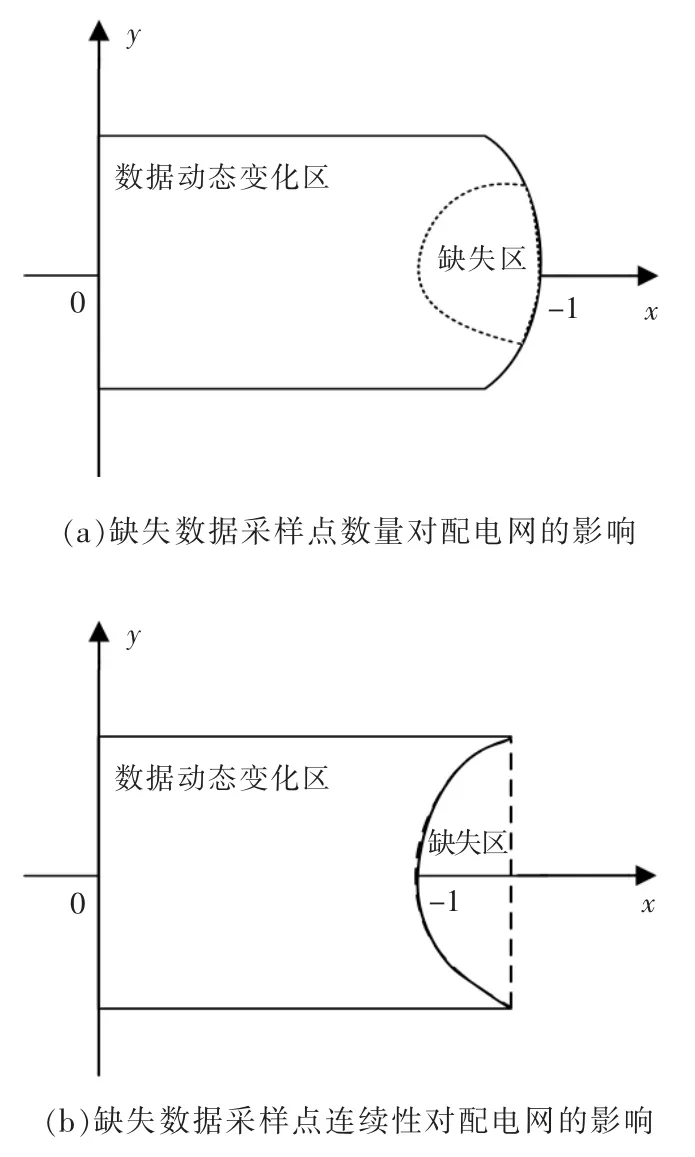
图1 缺失数据采样点和连续性对配电网的影响Fig.1 Impact of missing data sampling points and continuity on distribution networks

由图1 可知，当缺失数据数量出现大范围变化时，会造成电网其他区域的数据缺失，其中采样点连续性的整体影响面较大。根据不同状态下的配电区域缺失数据变化，结合上述过程的相似性数据判定分析，将缺失数据集状态矩阵表示为

若状态矩阵参数xij（i=1，2，…，n；j=1，2，…，m）为配网线损缺失数据项，配网线损在线监测数据缺失自适应填补的实现过程如下：将第j 个配网线损在线监测数据与其他相关联属性数据组成K 个组，假设缺失数据xij在第k（k=1，2，…，K）组中，此时，对缺失数据xij的填补数据方差为

式中：E 表示期望变量；Y2表示自适应填补参数。通常情况下，在配网线损在线监测数据缺失进行自适应填补时，由于缺失属性判定不一致导致的填补误差较大，且过于粗糙。针对该问题，采用加权类平均填补法，赋予每组缺失数据不同的损失函数权重，按照权重匹配实现配网线损在线监测数据缺失精确化填补，表达公式为

式中：ωk表示该组数据的填补权重；μk表示修正系数。通过上述过程，可以实现配网线损在线监测数据缺失自适应填补，且所需运算较少，通过赋予每组缺失数据不同的权重确保了填补的精准性，整体实用价值较高。

4 性能测试

4.1 实验设置

为验证文中提出配网线损在线监测缺失数据自适应填补方法的有效性，选取2022 年5 月1 日～6 月1 日间某地区的配网线损在线监测数据作为实验数据。为提高缺失数据填补效果的对比性，在原本不存在缺失数据的原始数据集中设置有25%的监测数据缺失，缺失区域有5 个。实验数据相关参数如表1 所示。

表1 实验数据相关参数Tab.1 Experimental data related parameters

4.2 缺失区域定位

以上文数据集为基础，运用本文聚类方法进行缺失区域定位，缺失区域定位结果如图2 所示。

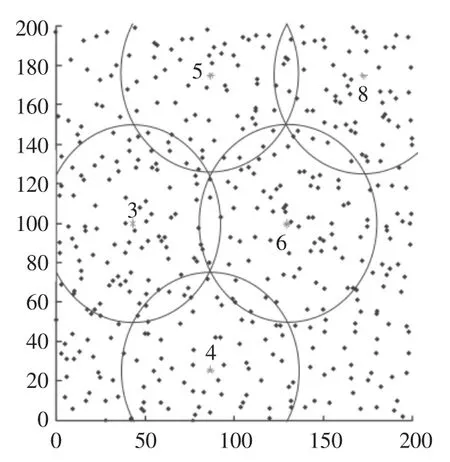
图2 缺失区域的定位Fig.2 Location of missing areas

通过图2 可以看出，本文方法很好地定位出5个数据缺失区域，定位效果较好。

4.3 缺失数据自适应填补结果对比分析

将基于次序依赖的配电网损坏数据自动填补算法、基于DBSCAN 二次聚类的配电网缺失数据修补法作为实验对比方法，并将未填补前配网线损在线监测数据作为参照，实现精准比对，实验结果如图3～图6 所示。

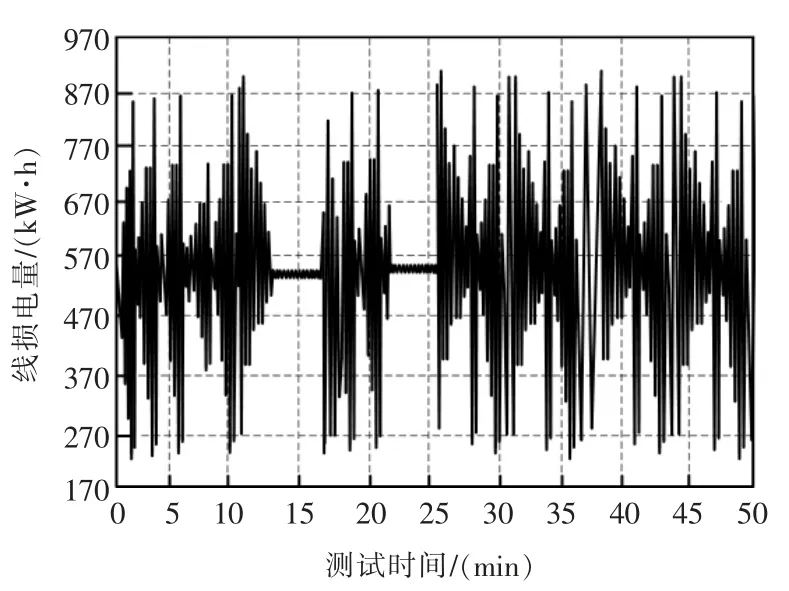
图3 未填补前配网线损在线监测数据变化Fig.3 Changes in online monitoring data of distribution line loss before filling

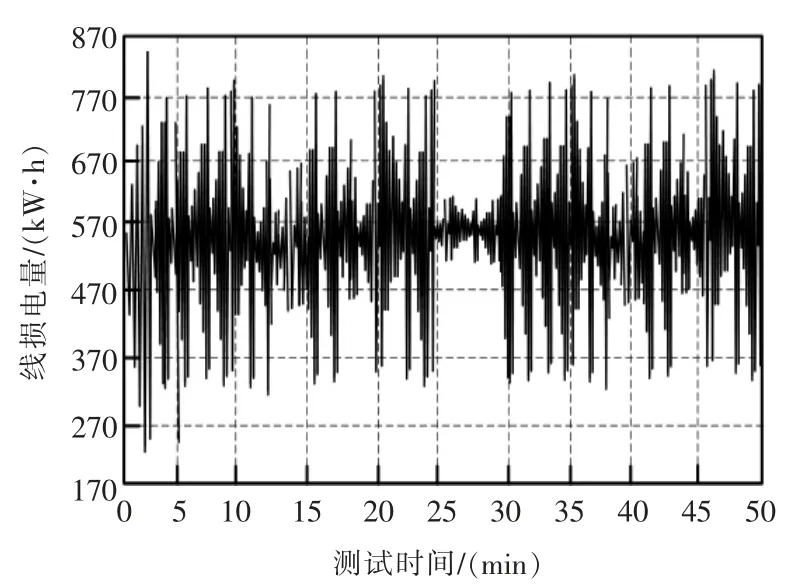
图4 次序依赖法填补后的数据变化Fig.4 Data changes after filling in the order dependency method

图5 DBSCAN 二次聚类法填补后数据变化Fig.5 Data changes after filling in DBSCAN secondary clustering method

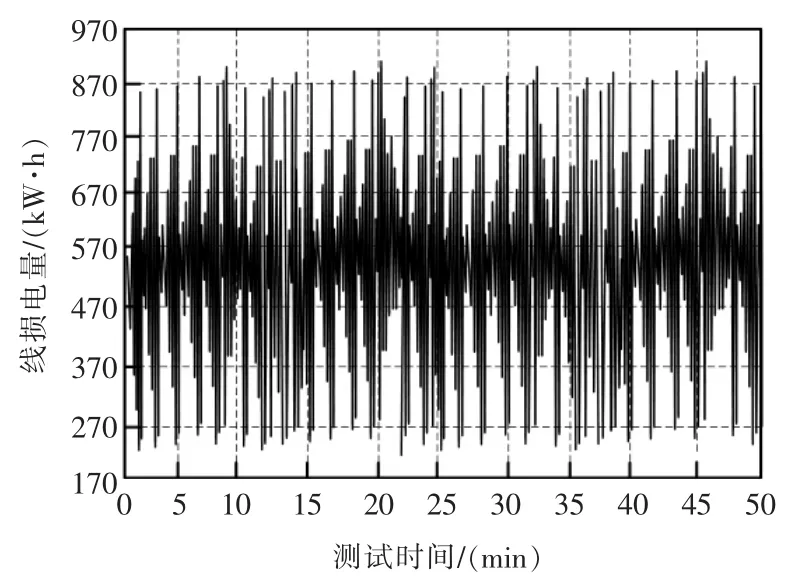
图6 本文方法填补后数据变化Fig.6 Data changes after filling in the method in this article

分析未进行自适应填补前配网线损在线监测数据变化情况可知，整体呈现较为混乱的变动趋势，线损电量曲线存在较大空缺和留白，不存在规律变化，说明受缺失数据影响，电网运行不稳定。经过3 种方法的自适应填补后，线损电量曲线得到明显的改善，但从细节对比可发现，本文的填补效果表现最佳，填补节点位置与原始数据缺失位置一致，填补后线损电量分布更为规律，更加稳定；而另外2 种方法填补效果明显不佳，填补位置与实际缺失位置不匹配，存在一定的填补误差，精准度较低，实用效果不佳，应用价值较低。

3 种方法填补结果的绝对误差值与相对误差值对比结果如表2 与表3 所示。

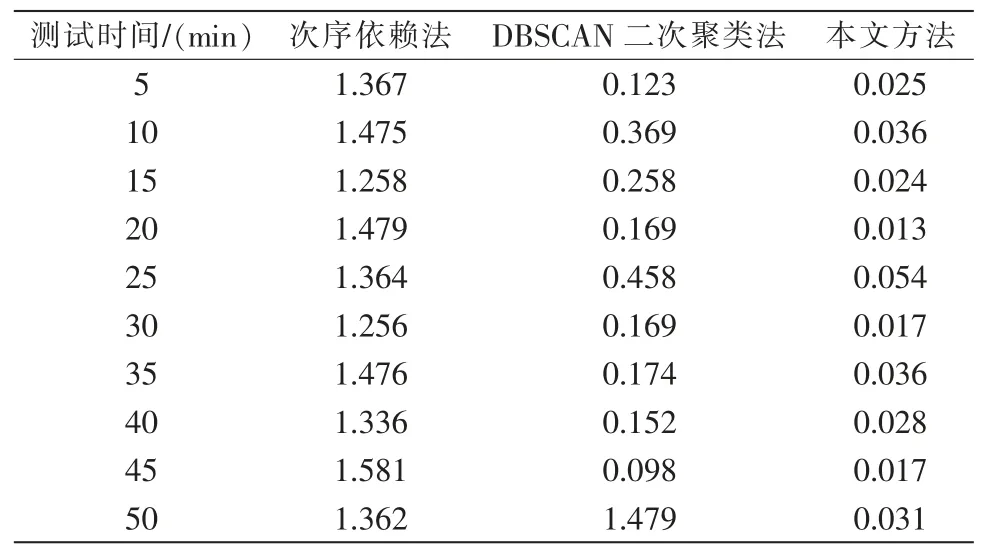
表2 3 种方法的绝对误差值比较Tab.2 Comparison of absolute error values of three methods

表3 3 种方法的相对误差值比较Tab.3 Comparison of relative error values of three methods

分析表2 与表3 中的数据可知，与次序依赖法、DBSCAN 二次聚类法这2 种方法相比，本文方法的配网线损在线监测数据缺失自适应填补结果的绝对误差值与相对误差值均保持在较低的水平，说明本文方法的填补效果更好。

5 结语

本文以配网线损在线监测数据缺失情况为基础，采用加权类平均算法进行自适应填补研究，得出以下几点结论：①本文考虑到电网在线监测数据量较大，基数较高，缺失数据种类较多的问题，在进行填补前，采用聚类算法对数据进行聚类处理，形成包含同种属性的聚类簇，通过查找损失量最大且与该样本相似性最高的数据点确定缺失点位置；②采用加权类平均填补法赋予每组缺失数据不同的权重，通过权重匹配实现数据缺失自适应填补。实验数据证明，本文方法对自适应填补效果较好，填补后电网运行更稳定，且填补结果的绝对误差值与相对误差值均保持在较低的水平，实际应用效果好。