基于序列二次规划法的铝型材截面优化设计*

张 衡,凌四营,张志豪,刘远航,凌 明

(大连理工大学微纳米技术及系统辽宁省重点实验室,大连 116024)

0 引言

工业快速发展的同时也伴随着严重的能源短缺和环境恶化问题,在机械结构设计过程中,为了保证构件使用的安全性,所设计的结构大部分拥有过多的强度储备[1],虽然在一定程度上大幅度提高了单个零件的使用寿命,但却使得整个装置变得笨重,最终在集成化、轻量化技术快速发展的过程中逐步被淘汰。因此节能和环保作为工业发展的重要方向,新材料、新结构、新工艺等轻量化技术是实现节能和环保的有效途径之一,其技术的广泛应用对制造业有着举足轻重的影响[2]。铝型材作为一种优质的铝合金材料,具有硬度高、耐磨性能好等突出特点,其耐腐蚀性能在经过阳极氧化处理后也会大幅度提高,在潮湿环境中不易生锈,同时化学性能稳定,可以重复回收利用,尤其在汽车工业领域及轨道交通发展等方面铝型材有着巨大的需求[3]。为了满足工业快速发展的需求以及提高铝型材生产的经济效益,就必须采用轻量化技术降低新产品的开发成本。

经过国内外专家学者的不断努力,智能优化算法快速发展并在轻量化技术方面得到了极大的应用。GRAF等[4]提出采用粒子群优化算法、最小二乘法以及基于有限元分析结果的新的非迭代尺寸匹配和缩放方法进行实现格子结构轻质和高刚性的能力;WEHRLE[5]采用无源数字解调算法得到强度噪声传播的统计模型,进行包括耐撞性在内的电动汽车结构轻量化设计;杨丁等[6]采用中心引力搜索算法进行起重机箱梁结构轻量化设计;李佐斌等[7]采用拓扑结构轻量化设计方法及变密度法分别对起重机的主梁和腹板进行拓扑优化;申士林等[8]采用基于神经网络的响应面法与多目标遗传算法相结合进行吊臂结构的优化设计,具有广阔的应用前景和使用价值。

上述方法优化效果不一,同时也推动了智能优化算法在轻量化技术中的应用,在一定程度上提升了收敛效率,但对于一些非线性程度较大的极限状态方程仍存在收敛性及计算精度不足的问题。本文采用有限元分析及序列二次规划算法进行铝型材的截面优化设计,在保证可靠性的同时提高收敛效率,达到结构轻量化的目的。

1 铝型材截面结构分析

1.1 性能指标

选定的铝合金型材型号为YK3984(6063-T5),铝型材初始截面如图1所示,截面中部直径为φ12 mm的圆孔需要攻丝(M14),截面四角使用时同样需要攻丝(M6),初始截面面积为967.00 mm2,线密度为2.62 kg/m,且截面的初始惯性矩已知(Ix=63.247 1 cm4,Ix=16.596 7 cm4),该截面图形为中心对称结构。

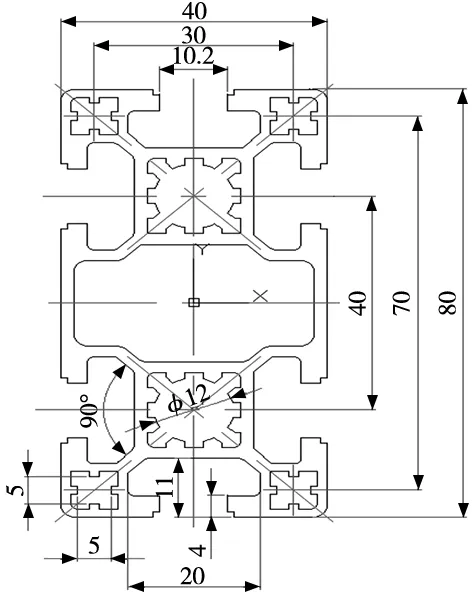
图1 铝合金型材截面

由于铝合金型材在使用过程中主要受到弯矩及扭矩的作用,需要保证其使用性能,即铝型材的抗弯及抗扭能力[9],在铝型材的型号选定的情况下,由下列抗弯及抗扭式(1)和式(2)可知其抗弯及抗扭性能取决于截面惯性矩。

(1)

(2)

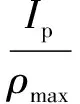
1.2 有限元分析

采用有限元分析的目的是观察铝型材截面承受载荷情况下,整体及截面的应力及应变,便于进行结构改进及截面设计参数的选取。

根据CAD二维图纸数据,首先在UG12.0软件中绘制草图,然后建立图2所示实体模型,并导入至ANYSYS软件中,单击工具栏中指派材料图标为实体模型选取材料,根据6063型号铝型材的属性填入相关的弹性模量、密度、泊松比等参数,如表1所示。

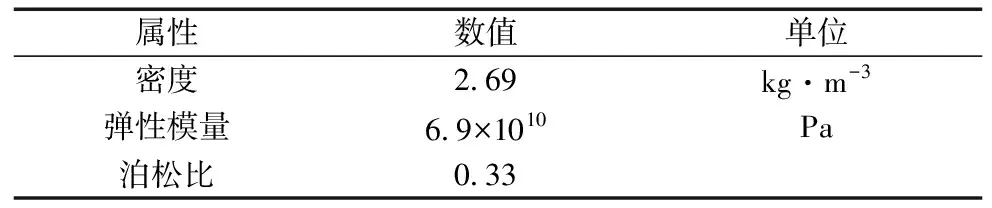
表1 铝型材材料属性

图2 铝型材三维模型

在工具栏中采用3D四面体网格,选定铝型材实体,选择网格单元大小及其他参数设置,施加载荷及约束,考虑到铝型材在实际应用中[10],大多情况下在两端处与相同件进行连接,中间跨距不大,且适当距离由支撑连接,因此约束形式为两端固定的方式,在中部施加均匀载荷。

点击求解后会出现多个对话框,等求解完毕后关闭对话框即可,求解完成后查看左下角结果,查看铝型材的应力云图,如图3所示。

图3 应力云图

由图3可知,铝型材在使用过程中受力情况,在中部最大形变截面处,开有安装槽部位受载荷影响较小,型材外围平面受载荷影响相对较大,为之后截面结构优化提供依据。

1.3 结构优化参数

设任意平面图形的形心为C,面积为A,xc轴和yc轴为图形的形心轴,y轴平行于yc,两轴之间的距离为b,x轴平行于xc,两轴之间的距离为a,由惯性矩的平行移轴公式可知,平面图形对于任意轴的惯性矩,等于图形对与该轴平行的形心轴的惯性矩加上图形的面积与两周距离的平方,可表示为:

Ix=Ixc+a2A

(3)

Iy=Iyc+b2A

(4)

根据式(3)和式(4)可知,材料集中在离轴线约远越好,所以尽量减少离轴线近的材料,增加离轴线远的材料,但也要兼顾铝型材的受力情况,以满足正常的使用要求。结合有限元分析情况,将靠近中心轴线且受载荷影响不敏感的截面面积减小,增大离中心轴线距离远且受载荷影响较大的区域面积。选定区域后,结合CAD中面域指令,在选定区域内将原图形截面结构进行优化调整,初步得到如图4所示改进后的铝型材截面结构。

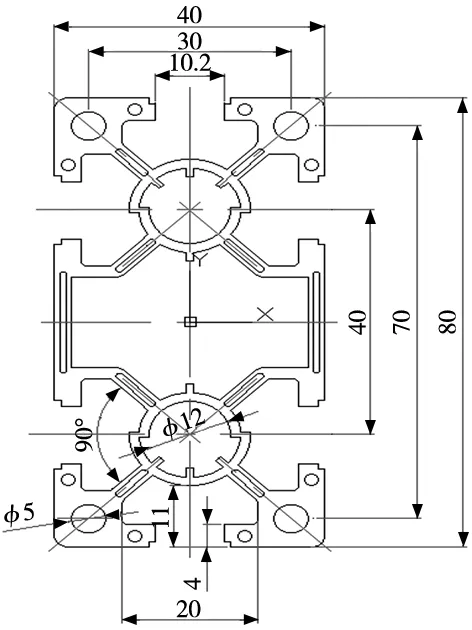
图4 截面结构优化图

图4为中心对称结构,因此只需对截面的1/4部分进行分析。以截面左上角部分为例,选定的截面设计变量空间位置如图5所示,设计变量的取值区间及初始值如表2所示。

表2 设计变量及区间

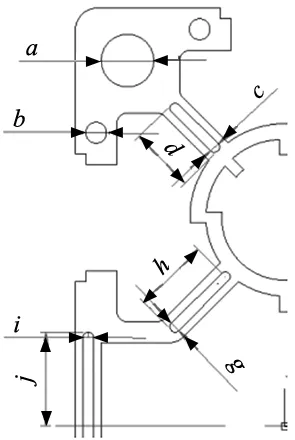
图5 设计变量

2 铝型材截面参数化

2.1 截面面积

设计参数变化引起截面面积发生变化,因此采取以面积最小时的图形为基准,加上与参数有关的面积,容易得到截面图形面积S公式,可表示为:

S=1072.5917-πa2-2πb2-4(cd+gh+ij)

(5)

2.2 截面惯性矩

根据截面惯性矩的定义[11],任意组合图形对某一轴的惯性矩等于组成它的各个简单图形对同一轴惯性矩之和,所以在计算截面惯性矩时,采用与计算面积相同的原理,由初始截面惯性矩和参数取值范围得到截面惯性矩的最小值,然后加上含参数的截面惯性矩。

静矩作为构件的一个重要的截面特性,表示微元面积与每一个微元与截面上指定轴线距离乘积的积分,同时也可表示为截面上某一部分的面积乘以此面积的形心至整个截面的型心轴线之间的距离[12]。取微面积dA,dA的坐标分别为y和x,则ydA和xdA分别称为微面积dA对于x轴和y轴的静矩,它们对整个截面图形面积的积分分别称为整个截面图形对于x轴和y轴的静矩(Sx,Sy),可分别表示为:

(6)

(7)

平面图形对某轴线的静矩等于其面积A与形心坐标(形心至该轴线的距离)的乘积,平面图形的形心坐标可以表示为:

(8)

(9)

在结构设计和计算的过程中,需要计算构件在弯矩作用下分别绕x、y轴的截面抗弯刚度,以满足构件的使用需求。惯性矩Ix、Iy为截面各个微元面积与各微元至与x、y轴线平行或重合的中心轴距离二次方乘积的积分,可表示为:

(10)

(11)

采用上述公式,截面图形的惯性矩可表示为:

(12)

(13)

3 优化方法

3.1 优化问题

优化问题的设计目标是使铝型材截面面积S最小化,限制条件为设计变量的取值范围及截面惯性矩不减的要求。

3.2 优化过程

非线性约束最优化问题:

minf(X)
s.t.gu(X)≤0 (u=1,2,…,p)
hv(X)=0 (v=1,2,…,m)

(14)

式中:f(X)为优化目标,gu(X)、hv(X)分别为不等式、等式的约束条件。

利用泰勒展开把非线性约束问题式(14)的目标函数在迭代点X简化成二次函数,把约束函数简化成线性函数后得到的就是如下的二次规划问题:

(15)

为了解决近似原约束最优化问题的解不一定是原问题可行点的情况,所以令:

S=X-Xk

(16)

将上述二次规划问题转变成关于变量的S的问题,可表示为:

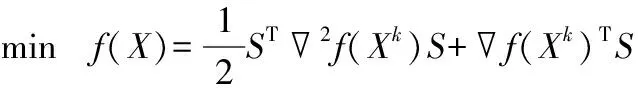
(17)

令:

H=2f(Xk)
C=f(Xk)
Aeq=[h1(X),h2(X),…,hm(X)]T
A=[g1(Xk),g2(Xk),…,gp(Xk)]T
Beq=[h1(X),h2(X),…,hm(X)]T
B=[g1(Xk),g2(Xk),…,gp(Xk)]T

式(17)所述的二次规划问题的一般形式可表示为:

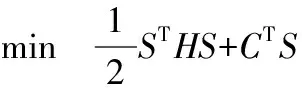
(18)

利用变尺度法中的DFP公式或BFGS公式进行二阶导数矩阵的近似计算,可分别表示为:

(19)

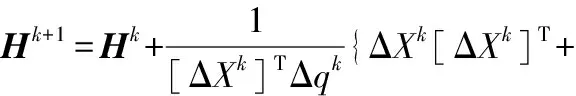
(20)

为解决上述二次规划问题,在迭代点Xk上先进行矩阵Hk的变更,构造和求解相应的二次规划子问题,并将该问题最优解S*作为下一次迭代的搜索方向Sk。然后在该方向上对原非线性最优化问题目标函数进行约束一维搜索,就可以得到下一个迭代点Xk+1,同时判断收敛精度是否满足要求,重复上述过程直至达到迭代点Xk+1满足终止准则,即可得到原非线性最约束问题的最优解Xk。

综上所述,序列二次规划算法的迭代步骤[14]为:

步骤1:首先给定初始点X0、设定收敛精度,令H0=1(单位矩阵),设置k=0;

步骤2:在点Xk将原问题简化为一般二次规划问题进行求解;

步骤3:求解一般二次规划问题,并令Sk=S*;

步骤4:在方向Sk上对原问题目标函数进行约束一维搜索,得到点Xk+1;

步骤5:如果Xk+1满足给定精度的终止准则,那么令X*=Xk+1,f*=(Xk+1),输出约束问题的最优解,终止计算,否则进行下一步;

步骤6:按式(19)或式(20)修正Hk+1,令k=k+1,转到步骤2继续进行迭代。

3.3 优化结果

将设计变量及截面参数模型代入优化算法得到设计变量的最优解如表3所示。

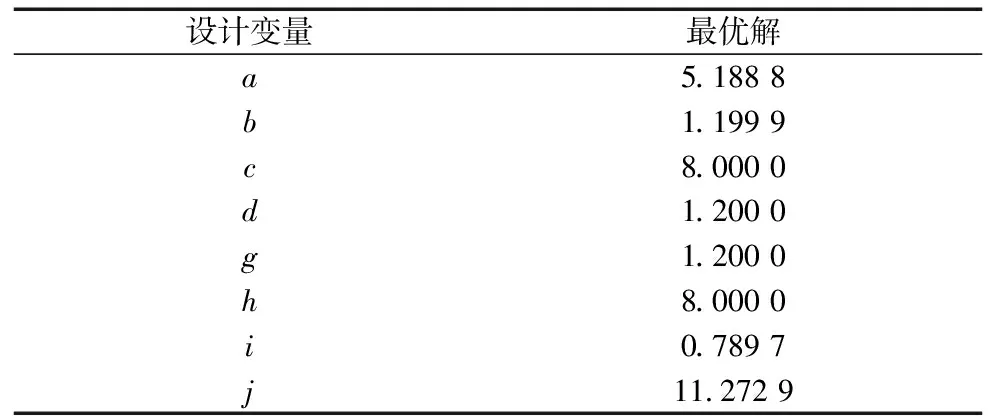
表3 设计变量最优解 (mm)

经过序列二次规划算法得出满足要求的最优解,将其分别代入式(5)、式(12)和式(13)可以得到优化后的截面面积及惯性矩。

由表4可知,通过对比优化前后的结果,发现优化后的截面惯性矩不减,截面面积优化后相比优化前减少了10%。

表4 优化结果

4 结论

通过分析铝型材的抗弯及抗扭性能,得到其性能指标,采用有限元分析软件对铝型材截面结构进行改进,选用合适的设计变量并建立了截面面积及惯性矩的参数化模型,与CAD辅助计算结果相比误差不大于0.5%,基于序列二次规划算法完成了铝型材的截面优化设计,在保持铝型材截面惯性矩不减的情况下,通过优化减小其截面面积以达到铝型材轻量化的目的,优化后截面面积减少了10%,实现了铝型材截面优化设计及轻量化的目标。