特长隧道内列车车内压力波模拟方法分析

陈春俊 ，王熙茹，周敏

(1.西南交通大学 机械工程学院，四川 成都 610031；2.轨道交通运维技术与装备四川省重点实验室，四川 成都 610031)

西部山区铁路是我国“十四五”规划国家铁路建设的头号工程。其中某线路整体走向“八起八伏”，累计爬升高度达到1.4万m，修建难度举世罕见。为适应复杂线路环境，沿线设计了大量隧道，其中长度超过30 km 的隧道有6 座，最长的隧道甚至达到了42.5 km[1]。按照划分标准，长度在10 km 以上的隧道称为特长隧道，西部山区铁路背景下大量特长隧道的设计对运行列车的动态气密性和车内压力控制提出了更高的要求与挑战。因此，开展该工况下的空气动力学问题研究对保障线路安全运行、提高舒适性有着重大意义。但由于西部山区铁路正在修建中，无法通过现场测试为研究提供数据支撑，如何获得西部山区铁路特长隧道工况下的车内压力波动数据成为了一项亟待解决的问题。当前研究中，获取车内压力大致有2种方法。一种是线路测试，学者们通过测试获得压力数据，对不同隧道长度[2-3]、列车维修等级[4]的气密性、压力舒适性进行分析。另一种是数值模拟或数学模型计算，根据计算原理可大致分为3类：1) 三维数值模拟。GOELZ 等[5]利用该方法对车厢通风系统的结构设计提供指导；LI 等[6-7]研究了不同线路和泄漏面积下列车的气密性；骆建军等[8-9]也分析了海拔高度的影响，提出了不同海拔下的列车气密性指数要求。2) 一维数值模拟。WILLIAM-LOUIS 等[10]提出了车内外压力波动的一维数值模拟方法；PALMERO 等[11]借此研究了特长大坡度隧道内的压力舒适性问题；梅元贵等[12]在此基础上结合广义黎曼特征线法进行求解，对高速磁浮单列车通过隧道[13]和在隧道内交会工况下[14]的压力波动进行了研究。3) 车内外压力传递模型。KWON[15]利用气密性指数计算公式提出了车内压力的数学计算公式；陈春俊等[16-18]从车内外压力传递机理出发，提出了多因素耦合作用下的车内外压力传递函数模型。综上所述，对于难以进行线路测试的隧道工况，学者们提出了多种车内压力模拟方法，但由于模拟方法的计算原理、模型机理不同，其模拟效率、计算精度和适用场景也有所差异。目前，未见对于不同车内压力模拟方法的系统比较，不同特征工况下车内压力模拟方法的选择存在缺乏支撑依据、计算精度难以准确评估等问题。为此，本文基于西部山区铁路特长隧道车内压力模拟研究的应用背景，对三维数值模拟、一维数值模拟和车内外压力传递模型3种车内压力模拟方式进行分析评价，将不同模拟方法在同一工况下的计算结果与实测结果进行对比，评价各模拟方法的计算精度。评价指标包括4 个方面：车内压力波动均方根误差、峰值、变化量最大值和动态气密性指数。根据评价结果，结合模拟效率、计算条件对不同模拟方法的适用场景进行分析，为特长隧道耦合作用下的车内压力模拟方法的选择提供依据。

1 车内压力模拟方法理论基础

1.1 三维数值模拟方法

车内压力的数值模拟是通过建立空气流动方程，用合适的算法和边界条件对离散后计算域内各节点的流动参数值进行求解，并用离散值代替实际物理场上连续参数值的计算方法。在三维数值模拟中，流动方程为三维空间中建立的质量、能量、动量守恒和气体状态方程。该方法适用性强，应用面广，能够对复杂几何结构和边界条件的计算域进行求解，但计算量较大，需要较高的计算机配置。

以某型号高速列车二等车车厢为研究对象，建立如图1(a)所示的1∶1 三维计算模型，并基于三维不可压缩非定常雷诺时均Navier-Stokes 方程和Realizablek-ε2 个方程的湍流模型对换气风道和车体缝隙影响下的车内压力展开计算[19-20]。控制方程离散格式采用2阶迎风格式，离散控制方程组的求解采用SIMPLE 算法，瞬态计算时间步长为1×10-4s。其中，车厢全长24.8 m，宽3.27 m，高3.89 m，模型内包括空调机组、列车风道等部件。此外，为模拟车体缝隙等效泄漏面积动态变化的影响，将不同时段的气密缝隙泄漏面积转化为直径不同的等效泄漏圆孔[7]，其转换结果如图1(b)所示。在图1(b)中，A 和B 区域使用固定值替代连续变化值，其中Actual Leakage Area 为实测泄漏面积，Equivalent Leakage Area 为等效后泄漏圆孔面积，对应图1(a)中不同直径等效泄漏圆管的面积，管长为车体厚度。在后续的计算中，通过将各时刻对应面积的等效泄漏圆孔底面设置为空气交换边界，即可模拟列车运行过程中等效泄漏面积的变化。

计算域包含2个部分，分别为车厢内流场和用于在等效泄漏孔外部加载压力波的压力传递区，二者通过等效泄漏圆孔连接，如图2 所示。其中，列车新风口和压力传递区入口为压力入口边界，压力值为利用UDF 编译的实测车外压力。废排口和压力传递区出口为压力出口边界，压力值为大气压力值。压力传递区的其余壁面设置为滑移壁面边界条件。换气装置采用风机边界，设定实测风机流量曲线为压头函数，模拟泄漏孔在面积变化处为内部面边界，车体模型及泄漏孔的其余边界均设置为静止壁面边界。

图2 计算域及边界条件Fig.2 Computational domains and boundary conditions

参考文献[20]，采用四面体非结构化网格划分计算域，为消除网格尺寸对计算结果的影响，划分3套不同尺寸网格，并选用车内中部压力和泄露孔流量作为检验标准，结果如表1所示。随着网格数量的增加，压力和流量计算误差分别为1.1%，1.6%和1.5%，1.6%，满足计算精度要求。故选用中等网格组，计算域最大网格尺寸为90 mm，风口最大尺寸为10 mm，泄漏孔最大尺寸为3 mm。划分结果如图3所示。

表1 不同网格密度下t=2 s时刻车内中部压力及泄露孔流量Table 1 Air pressure and leakage hole flow in the middle of the train at time t=2 s under different grid densities

图3 网格划分结果Fig.3 Meshing result

1.2 一维数值模拟方法

隧道内空气动力学现象研究表明[21]，长度尺度远大于径向尺度隧道内的空气流动具有显著的一维流动特征。基于此，学者们提出了一维数值模拟方法[10]，该方法忽略了径向截面上的气体流动，将流动方程由三维简化为一维。一维数值模拟计算思路与三维的相近，同样是对偏微分方程进行离散和数值求解，但方程的简化降低了计算量，使得在三维模拟中难以计算的长隧道能够利用该方法计算。但由于计算方法中离散与近似的思想，使得结果很大程度上依赖于所建立的数学模型，故该简化势必会造成一定的计算误差。

本文所用一维模拟方法如文献[21]所述，视车内压力波动由列车当量泄漏面积引起，计算思路为：将当量泄漏面积视为均匀分布在车体长度范围上的小细孔，根据喷嘴流量公式可知气体交换流量的计算式：

式中：下标Q 表示流入空间；下标R 表示流出空间；γ为比热比；a为声速；p为空气压力；t为时间；FT为小细孔的有效流道横截面积，可通过车体静态气密性试验[22]确定。与三维数值模拟需已知车外压力不同，车内压力的一维数值模拟是耦合计算的，可直接计算出车外压力，并利用公式(1)进一步得出车内压力。

1.3 车内外压力传递模型

车内外压力传递模型是从车内外气压传递机理出发，为优化列车压力控制系统，缓解压力舒适性问题而提出的。该模型基于动态气密性试验、车体流固耦合计算和换气风机工作曲线测试结果，分析了气密性缝隙、车体变形和换气风道3个因素对车内压力的影响，建立了多因素耦合作用下的车内外压力传递模型[16-18]。该模型计算量小，可利用车外压力快速得出车内压力，适用于车内压力控制问题的研究。但由于将各因素的影响转换成了数学模型，会造成一定的计算误差，影响该方法的适用性。

其中，通过气密性缝隙的气体质量流量表达式qg见公式(2)，不同阀门开度下的新风机和废排风机气体质量流量qN和qW的表达式见公式(3)和(4)，不同压差作用下车厢体积V(k)的计算式见公式(5)。

由于车内外气体传递遵守质量守恒定律，联立气体绝热等熵方程和理想气体状态方程，可得如公式(6)所示车内压力变化量ΔPi与气体质量流量变化量之间的关系式，随后代入公式(7)可求得下一时刻车内压力：

式中：Pi为车内压力；Pe为车外压力；ρ为气体密度；Seq为等效泄漏面积；Cv为阀门相对流量系数；M为气体摩尔质量；T为热力学温度；R 为理想气体常数；Δk为时间步长；V0为车内净体积。

2 车内压力模拟方法的精度分析

本节将同一工况下3种模拟方法计算结果与线路测试结果对比，分析不同车内压力模拟方法的计算精度。考虑到车内压力的主要研究内容，从以下4 个方面进行对比：车内压力波动均方根误差、峰值、压力变化量最大值和动态气密性指数。

线路测试以某型动车组中间车为测试对象，测量其以300 km/h 的速度通过1 067 m 长的隧道时的车内外压力。数据采集系统采用IMC 8通道数据采集器，采样频率1 000 Hz，传感器为贴片压阻式压力传感器，量程为105 kPa，灵敏度为1.92 mV/kPa。如图4(a)所示，测点布置在列车中部同一横截面上，车外测点在靠近隧道壁面一侧的外表面上，车内测点在乘客头部位置附近的车体内表面上。为验证线路测试结果的重复性和可靠性，进行了2 次测试，其结果如图4(b)所示，其中Pi为车内压力，峰峰值为390.84 Pa 和380.27 Pa，误差为2.70%。Pe为车外压力，峰峰值为2 561.13 Pa 和2 540.32 Pa，误差为0.81%。由上述测试结果可知，该测试结果重复性好、可靠性高。选用第1次测试结果与模拟结果对比，分析各模拟方法的计算精度。

图4 现场测试测点分布及测试结果Fig.4 Distribution of test points and test results

2.1 车内压力波动均方根误差分析

图5 为3 种模拟方法在同一工况下的计算结果与线路测试结果的对比图，图中Pi表示车内压力，Actual Measured 为测试结果，Three Dimension 为三维数值模拟结果，One Dimension 为一维数值模拟结果，Model 为车内外压力传递模型计算结果。为了更好地评价模拟结果与实测结果在波动趋势上的吻合程度，使用均方根误差值来衡量模拟结果与实测结果之间的差距，其中均方根误差值的定义式为：

图5 车内压力模拟结果Fig.5 Simulation result of train internal pressure

式中：erms为均方根误差值；N为数据点数；Pi为模拟得到的车内压力数据；A_Pi为实测车内压力数据。

根据公式(8)计算得到的均方根误差值如表2所示。由图5 及表2 可知，上述3 种模拟方法都能大致模拟出车内压力波动趋势，其中一维数值模拟的均方根误差值最小，准确性最高，而三维数值模拟结果与实测结果相差较大，主要体现在图中A1和B1区域，是模拟中对等效泄漏面积的简化处理导致的，对应图1(b)中的A和B区域。三维数值模拟在等效计算过程中以固定值为等效泄漏圆孔面积，替代了实际上随时间不断减小的气密性缝隙，故在图5 对应的A1和B1区域中三维数值模拟结果在波动趋势上与实测结果存在一定差距。

表2 车内压力的均方根误差值Table 2 Root mean square error of train internal pressure

2.2 车内压力波动峰值分析

表3为线路测试结果与计算结果在压力峰峰值上的对比情况，表中峰峰值为具体压力值，百分比表示模拟结果与实测峰峰值的百分比。由表3可知，一维数值模拟结果与测试结果最为相近，比值达到99%，三维数值模拟和车内外压力传递模拟的计算结果相近，但计算精度较低，比值仅达到实测结果的84%。

表3 车内压力峰峰值Table 3 Peak value of pressure inside the train

2.3 车内压力变化量最大值分析

人耳平衡外部压力变化所用时间一般为3～4 s，当外部压力变化剧烈，人耳无法及时平衡耳膜两侧压差，将引起人耳感不适[23]。故从车内压力舒适性评价指标出发，取1，3 和4 s 时间间隔，计算不同时间间隔内压力变化量的最大值。其中，压力变化量是指压力在一定时间内最大值与最小值之差，计算公式为：

式中：Pi表示车内压力；ΔPn为ns时间内车内压力变化量(n=1，3，4)。

根据公式(9)计算得到的车内压力变化量最大值如图6所示，柱状图的高度对应压力变化量最大值的数值，图中的百分比为不同时间间隔内模拟计算结果与实际测试结果的比值。由图6可知，随着时间间隔的增加，车内压力变化量最大值的数值大小也逐渐增加。三维模拟仿真对压力变化量最大值计算结果的计算精度较高，占实测结果的80%以上，但随着时间间隔的增大精度有所降低。一维数值模拟和车内外压力传递模型都是随着时间间隔的增大，计算结果与实测结果更为贴近。在4 s 时间间隔内，一维数值模拟结果达到了实测结果的86%，车内外压力传递模型计算结果达到了实测结果的65%。

图6 不同模拟方法车内压力变化量最大值对比Fig.6 Maximum variation of train internal pressure with different simulation methods

2.4 动态气密性指数分析

车体动态气密性指数是评估列车线路运行过程中气密性能的指标，反映了列车在隧道内运行时车辆真实的气密性指数[7]，其计算公式为：

式中：Pi为车内压力；Pe为车外压力；Δt为传感器的采样的时间步长；τ为车体动态气密性指数。

3 种模拟方法计算结果对应的动态气密性指数如表4所示。其中，车内外压力传递模型的计算结果与实测结果最接近，一维数值模拟仿真和三维数值模拟结果都与实测结果相差较大。这是由于车内外压力传递模型在计算车内压力时，综合考虑了通风系统、车体变形和车体气密性缝隙的影响，更贴合于实际情况。

表4 不同车内压力模拟方法的动态气密性指数Table 4 Dynamic airtightness index with different simulation methods

3 特长隧道车内压力模拟方法分析与模拟计算

为满足西部山区铁路特长隧道背景下列车空气动力学问题的研究需要，结合上述分析结果，对3种车内压力模拟方法的适用场景进行讨论，并综合考虑西部山区铁路特长隧道工况特征，为该应用背景下不同空气动力学问题研究时车内压力模拟方法的选用提供建议。

3.1 车内压力模拟方法分析

从模拟效率、计算精度和适用性出发，对不同车内压力模拟方法的适用场景进行分析。

其中，为了直观地体现不同模拟方法在模拟效率上的差距，对前文所述工况下的3种模拟方法的计算设备和计算时间进行介绍。三维数值模拟是在配备32 核心2.5 GHz 主频的x86 处理器，16 GB DDR4 2666 ECC REG 八通道内存的超算平台进行计算，计算时长为2083 核时。一维数值模拟和车内外压力传递函数模型计算是在配备2.4 GHz intel core i5 CPU,16 GB 1 600 MHz DDR4 双通道内存的笔记本电脑上进行计算，程序分别由FORTRAN 和MATLAB 编码，一维数值模拟耗时11.103 s，车内外压力传递模型为1.184 s。

综合3种模拟方法在不同指标中计算精度的分析结果可知：在所用的3 种车内压力模拟方法中，三维数值模拟计算结果的准确性是最高的，计算原理也是与实际空气流动情况最为贴近的，适用性强，应用面广。但存在计算量大、依赖于高性能设备等缺点，并需已知车外压力作为附加条件。因此，综合考虑计算效率，该方法更适用于中长或短隧道内列车空气动力学问题的研究。

所用的一维数值模拟计算结果在准确性上略低于三维模拟，但计算时间大大减少，且在计算中为耦合计算，无需已知车外压力，适用性强。因此，综合来看，一维数值模拟适用于长隧道、特长隧道内空气动力学问题的研究，或用于难以进行线路测试的隧道工况下车内压力波动问题的研究。

车内外压力传递模型的计算时间最短，但计算精度也最低。且由于将各因素的影响转换成了数学模型，适用性也是3种方法中最低的，同样需要已知车外压力作为计算条件。因此，车内外压力传递模型更适合在研究车内压力控制系统的优化中使用，通过控制车内压力波动以缓解乘客压力舒适性问题。

3.2 特长隧道工况下车内压力的模拟计算

根据上述车内压力模拟方法分析可知，在西部山区铁路特长隧道工况下，推荐使用一维数值模拟方法。为了验证该模拟方法在计算特长隧道工况时的正确性，将计算结果与文献[11]中的计算结果进行比较，工况为列车以300 km/h 通过长度为28.4 km 的特长隧道时列车头车的车内外压力波动，对比结果如图7(a)所示。其中，一维数值模拟计算结果与文献结果吻合较好，车外和车内压力峰峰值计算结果与文献结果的误差分别为2.00%和5.42%，该差异可能是文献中未完全给出计算所需空气动力学参数所导致的。

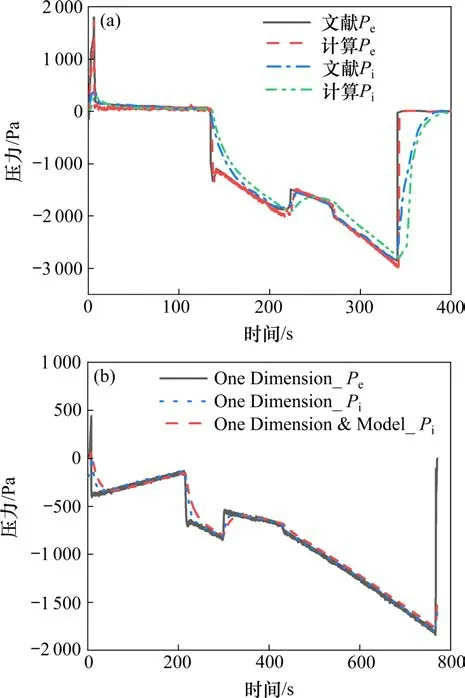
图7 特长隧道中头车车内外压力波动Fig.7 Pressure fluctuation inside and outside the head vehicle in extra-long tunnel

此外，考虑到西部山区铁路特长隧道背景下车内压力舒适性问题的研究需要，可使用一维数值模拟与车内外压力传递模型相结合的方法进行研究。即将一维数值模拟计算得到的车外压力代入车内外压力传递模型，计算出车内压力波动情况。该方法可对特长隧道内车内压力波动情况进行分析，为西部山区铁路背景下列车压力控制系统的优化提供支撑。开展特长隧道工况下的车内压力波动控制算法研究，即可通过抑制车内压力波动缓解特长隧道内的乘客压力舒适性问题。

为证明一维数值模拟与车内外压力传递模型相结合的计算方法的正确性，以西部山区铁路特长隧道的设计方案为参照，将该方法的计算结果与一维数值模拟直接计算结果进行对比。工况为列车以200 km/h 速度通过42.5 km 特长隧道，隧道净空面积为52 m2，其余隧道相关参数设定参考特长隧道设计情况，列车相关参数设定参考线路测试列车情况，其头车的车内外压力波动情况对比结果如图7(b)所示。其中，Pi为车内压力，Pe为车外压力，One Dimension 为一维数值模拟法，One Dimension &Model 为2 种方法相结合。由图7 可知，2 种方法计算结果吻合良好，峰峰值误差仅为1.36%。

4 结论

1) 综合来看，在本文所用的车内压力模拟方法中，三维数值模拟在预测车内压力变化时准确性最高，但受所需计算资源限制，考虑其计算效率，更适用于中长、短隧道工况下的车内压力模拟计算。

2) 一维数值模拟在预测车内压力波动时计算精度略低于三维数值模拟，但其计算量小于三维数值模拟，且无需已知车外压力作为计算条件。因此，该方法更适用于在建隧道、长隧道或特长隧道工况下的车内压力模拟计算，也是西部山区铁路特长隧道工况下推荐使用的压力模拟方法。

3) 车内外压力传递模型计算量最小，但计算精度和适用性差。相比于其他模拟方法，更适用于车内压力控制系统的优化设计研究。

4) 在研究特长隧道内的压力控制问题时，可将一维数值模拟方法与车内外压力传递模型结合使用，该方法计算结果与一维数值模拟直接计算结果吻合良好，车内压力峰峰值计算误差为1.36%。