自适应纹理区域的多尺度融合立体匹配算法
陈 艺,于纪言,于洪森
南京理工大学机械工程学院,南京210094
近年来,随着双目立体视觉在3D地图重建、目标检测、无人驾驶和虚拟现实等领域的广泛应用,双目立体视觉已经成为计算机视觉领域研究的热点。立体匹配是在同一时间点拍摄的不同视角的两幅或者多幅图像中寻找同一场景的像素匹配点,再通过逐像素点计算匹配代价,找到最优匹配像素点,计算出视差,进而得到真实空间的三维深度信息。Scharstein等人在总结已有的立体匹配算法后,提出了立体匹配的基本流程:匹配代价计算、代价聚合、视差计算和视差优化四个步骤。在采集双目匹配图像前,需要进行相机标定,主要可分为经典相机标定法、自标定法、主动标定法和基于深度学习标定法[1]。根据代价计算的方式不同,可以将传统匹配算法分为全局、半全局和局部三大类算法。其中全局匹配算法是通过建立全局能量函数,由优化理论求解最优化全局能量函数,常见的全局匹配算法有图割(graph cuts,GC)[2]、置信传播(belief propagation,BP)[3]和动态规划(dynamic programming)[4]等;半全局匹配算法(SGM)[5]虽然依然采用全局框架,但其在计算能量函数最小化的步骤时使用高效的一维路径聚合方法来取代全局算法中的二维最小化算法(即用一维来近似二维最优),相较于全局匹配算法,在得到的视差图误匹配率相差不大的前提下,其计算效率明显提升,但是其互信息法代价计算原理较为复杂,并且需要迭代计算,效率不高;局部匹配算法是依据一定大小的窗口内像素点,并计算寻找另外图像中像匹配像素点窗口,从而获得视差图,其有着匹配速度快,匹配精度较高,能够很好地应用于图像实时处理的过程中,常见的此类算法有灰度差绝对值(AD)、灰度差绝对值之和(SAD)、灰度差绝对值之和平方(SSD)和Census等。Mei等人[6]将AD和Census结合作为代价计算函数,相较于单一的代价函数计算函数,其能够很好地适应重复纹理和光照变化,闫利等人[7]将梯度与Census 结合起来作为代价函数,能够适应弱纹理区域,鲁棒性较好,Zhu等人[8]将颜色、梯度和Census变换相结合,将多尺度的变化量相结合,Nguyen和Ahn[9]将AD和SSD 代价函数加以改进,不仅可估计相应视差值,而且还利用扩展值r确定目标图像中的对应像素点,同时还改进了归一化函数NCC,并取得不错的匹配精度,冯彬彬等人[10]将SGM(半全局匹配算法)部署在FPGA上,实现了算法硬件加速,实时性大幅提升,Zhang等人[11]提出一种改进的最小生成树(MST)的代价聚合算法,取得了较高的匹配精度和匹配速度,Yao 等人[12]提出了一种混合代价聚合方法,可以评估像素之间的对应关系,在深度-不连续性区域中获得了较好的精度,宋嘉菲等人[13]对立体匹配深度学习模型中的采样方式进行改进,对于传统线性插值采样方式无法利用领域信息的缺点,其利用权重卷积窗口实现低分辨率采用高分辨率输出,Xu等人[14]提出自适应形状支持窗口的成本聚合方法,通过构建一个四方向的局部支持聚合骨架,同时扩展引导滤波来聚合成本量,其在深度不连续性和分段平滑区域方面取得了较好的匹配性能,畅雅雯等人[15]将HSV引入立体匹配的过程中,用Census 和梯度作为匹配代价函数,有效降低了对光照的敏感性。
针对传统单一算法的适应性不强,同时提高算法的强健性,能够应用在不同的场合,提出一种自适应纹理区域的多尺度融合立体匹配算法,在代价计算阶段,首先计算并划分出强纹理区域、弱纹理和无纹理区域,针对强纹理区域,使用AD 和Census 相结合计算代价,对于弱纹理和无纹理区域,考虑到梯度算子更能够反应微小像素值的变换,故采用AD和梯度相结合的算法计算代价;在代价聚合阶段,在强纹理区域,采用像素点距离和像素值之差作为十字交叉臂区域的构建约束条件,在弱纹理和无纹理区域,采用像素点距离和梯度值之差作为构建约束条件;最后,采用Winner-Take-All(WTA)策略进行视差计算,并利用扫描线优化和多步骤视差优化进行优化后处理,得到最终的视差图。
1 算法描述
所提算法的输入为经过矫正的双目摄像机立体图片,对输入左右图像进行代价计算、代价聚合、视差计算和视差优化后处理,整体流程图见图1所示。匹配代价计算时,针对强纹理区域、弱纹理和无纹理区域,分别选择AD+Census 和AD+梯度的代价计算函数,同时在划分区域过程中自适应调整阈值;代价聚合时,选用动态十字交叉域构造方法,在不同纹理区域分别选择不同的构建约束条件;视差计算采用WAT 策略计算每个像素点的最小代价值,进而得到视差图;最终对得到的视差图进行一系列后处理步骤,并输出视差图。

图1 整体算法流程图Fig.1 Overall algorithm flow chart
1.1 匹配代价计算
匹配代价计算是比较待匹配像素点和候选像素点之间的相关性,两像素点之间的代价越小,则说明两点的相关性越大(即两点为同名点的概率也越大)。通常用一个三维矩阵DSI(disparity space image)储存代价计算的结果,DSI的大小为H×W×D,其中H和W分别为图像的高和宽,D为视差范围。AD函数能适应重复区域匹配计算,且计算速度快,但是其对光照和噪声敏感,在弱纹理和无纹理区域的匹配精度很低[15];Census变换具有良好的鲁棒性,能够适应不同的光照和噪声,且弱纹理区域的匹配精度高,但其对于重复区域匹配精度很低[16];梯度算子能够显著提升弱纹理区域和无纹理区域的匹配精度,同时能够提高视差不连续区域和遮挡区域的匹配效果[17]。为了在所有可能出现的场景中都获得较高的匹配精度,例如重复区域、弱纹理区域、无纹理区域以及光照等外界因素,同时考虑到上述代价函数的特点,提出基于纹理区域的多尺度融合代价计算函数,在图像上不同的区域运用不同的代价计算函数,并自适应调节相应阈值,从而获得较高的匹配精度。同时由于没有预先实验,所以代价函数部分参数参考Liu等人所提出算法[18]中的实验结果。
首先需要区分开图像中的强纹理、弱纹理和无纹理区域,分别表示为Us、Uw、Un,将任意像素点周围n个像素点值进行相加并取平均值,常见的n可设置为四方向或者八方向,设置判断阈值τ,计算公式如下:
式(1)为利用周围像素点灰度值均值与阈值进行比较判断,式(2)为利用周围像素点三通道颜色值均值与阈值τ进行比较判断,Gi为像素点i的灰度值,flag为判断标志位,若为1,则此像素点属于Us;反之,则属于Uw和Un。
经过上式计算后,在强纹理区域使用AD 和Census相结合的代价计算函数,在弱纹理和无纹理区域使用AD和梯度相结合的代价计算函数。
AD函数的主要策略是不断比较左右图像中两点像素值大小,将待匹配图像的某一像素点的像素值取出,同时在另一幅待索引的图像中去寻找视差范围内最小代价值的像素点,计算表达式如下:
式(3)和式(4)分别为像素点灰度值和颜色值的代价计算公式,CAD( )p,q代表像素点p和q之间的AD函数计算代价值,G代表灰度值,I代表彩色三通道值,L和R分别代表左右相机两幅图像,p和q代表左右图像中的像素点。
Census 函数能够很好地检测出局部区域的结构特征,具有较高的匹配精度,对光照等外界因素适应性强,其主要策略是定义一个矩形窗口,长宽都为奇数,再用此矩形窗口遍历整个待匹配和待索引图像区域,并将窗口中心点的像素值设为中心值,同时对窗口内除中心点外的其他像素值与中心值进行比较,大于中心值则记为1;反之则记为0,将所得值映射为一个比特串,再对左右两幅图像的比特串进行异或,累加比特1的数目即可得到代价值。
式(5)~(7)中,p代表中心点,q代表中心点领域内的其他像素点,U为窗口内中心点的领域,Bp为求得的中心点处比特串,Bq为领域像素点比特串,将求得的左右图像比特串代入式(7)中得到汉明距,即Census代价值。本算法中梯度函数主要是使用sobel算子求解图像像素点的梯度值,主要计算方式如下:
上式中Gx和Gy分别为x和y两个方向上的运算子,将两个方向的运算子分别和左图像L和右图像R卷积得到两个方向上的梯度幅值,此处为简化运算,将两方向梯度绝对值相加得到总幅值。
所提算法将不同的代价函数加权融合,得到最终的代价计算公式,如下:
上式中将不同的代价函数归一化,且依据划分出的不同区域,使用不同的代价计算函数,cost取值范围在[0,2],λAD、λCensus、λGrad分别为三种代价函数归一化换算系数。
为了验证此算法代价计算的有效性,选择2003 年Middlebury数据集中图像cones,且都不经过代价聚合,只进行代价计算,获得的视差图见图2 所示。从图2 中可以看出,传统AD和Census结合的代价函数对于上侧深色框中的背景弱纹理处理效果优于传统AD 和梯度结合的代价函数,但对于下侧浅色框中的前后遮挡区域,AD 和梯度结合的代价函数处理效果优于AD 和Census结合的代价函数,而本文所提出的算法能够很好地综合前两者的优点,既能在背景弱纹理区域能取得比较好的效果,也能在遮挡区域和视差不连续区域获得较好的视差值。

图2 基于不同代价计算方法的cones图像的初始化视差图Fig.2 Initial parallax diagram of cones image based on different cost calculation methods
1.2 匹配聚合计算
传统的代价聚合都是采用统一的十字臂区域构建约束条件,即在弱纹理、无纹理区域以及强纹理区域都采用统一的臂长构建方法,这样的构建方式不能够适应复杂多变的环境,而且还有可能增加聚合中像素点代价的错误赋值,从而导致最终的误匹配率增加。例如在弱纹理和无纹理区域臂长设置过小,从而会导致中心点的像素代价值不准确。故所提算法在十字臂的构建过程中弱化了像素点值(颜色值或者灰度值)之差约束条件,而且添加梯度幅值之差的约束条件,使得在图片的弱纹理和无纹理区域的构建臂长变长,提高聚合的精度。传统CBCA算法[19]中十字交叉域构造的构建判断条件如下:
式(11)和式(12)中是为了限制两像素点p和q之间的颜色值之差的最大值,同时限制q与其相邻点q1的颜色值之差的最大值,其中q为领域像素点,p为中心像素点,Dc(p,q)表示p和q之间的像素点值之差,Ds(p,q)表示p和q之间的空间长度之差,并设置阈值τ1;式(13)中是为了限制两相邻像素点的空间位置长度,并设置阈值L。
后面为了使得十字交叉区域包含更多的像素点,将空间长度扩大L1>L,同时设置更加严格的颜色阈值τ2,在上面的基础上添加的判断条件表达式如下:
上式中当p和q两像素点的空间距离在[L2,L1] 之间时,将颜色值之差阈值设置为τ2(τ2<τ1),从而得到更大的臂长。
所提算法在代价计算过程中划分出不同纹理区域的基础上,在不同区域设置不同的判断条件,在强纹理区域设置颜色值之差和空间臂长之差两约束条件;在弱纹理和无纹理区域设置梯度和空间臂长之差两约束条件。具体表达式如下:
基于纹理区域动态十字臂区域构建结果如图3 所示,图3(a)和图3(b)中非空白区域为像素点动态支持域,深色为构建过程中的竖直臂和水平臂,构建支持域有两种策略,即先竖直后水平或者先水平后竖直,见图3所示。

图3 十字臂两种构建策略图Fig.3 Two construction strategies of cross arm
从图4(a)和(b)可以看出在弱纹理区域,传统CBCA算法中构建的十字支持域臂长小于本文所提出的十字臂长,即本文在弱纹理区域所构建的支持域能够包含更多的像素点;同时在强纹理区域,本文构建的支持域和传统的CBCA算法构建的支持域相差不大,都能取得很好的效果,如图4(c)和(d)所示。

图4 强纹理和弱纹理区域的十字交叉臂对比Fig.4 Cross arm comparison between strong texture and weak texture areas
1.3 视差计算
在代价聚合后,采用WAT(赢家通吃)策略计算每个像素点的最小代价,从而获得视差值,如式(16):
式(16)中D为视差范围,从而得到最终的视差值disp。
1.4 视差优化
经过代价聚合后的像素点视差值仍然有很多错误的匹配点,为了进一步降低误匹配率,需要进行后处理,步骤可以参照Liu 等人[20]和Guo 等人[21]提出的算法,先后进行左右一致性检查(L-R check),迭代局部投票和子像素优化三步。其中左右一致性检查是基于视差唯一性约束,剔除错误视差,表达式如下:
式(17)中DL(p)为左视差图的视差值,DR(p-dL)为右视差图对应点的视差值,通过比较两者的差值来提取出错误匹配点。
再对上面左右一致性检查处理后的无效像素点进行迭代局部投票,统计支持域内像素点在视差范围内直方图的得票,最终选择得票最多的像素点的视差值,判断表达式如下:
最后再进行子像素优化[22],通过一元二次拟合得到精度更高的视差值,表达式如下:
2 实验结果与分析
为了验证本算法的有效性和鲁棒性,采用Middlebury 2006数据集,实验中各参数设置如表1所示,用误匹配率来衡量算法的精度,设置视差阈值为1。

表1 实验参数设置Table 1 Experimental parameter setting
2.1 匹配代价计算验证
为了验证本算法的有效性和图像失真时鲁棒性,这里选取四种代价函数相对比,分别为SAD 和Census 相结合(SAD+Census)[23]、AD和Census相结合(AD+Census)[24]、AD和梯度相结合(AD+梯度)[20]及本文提出的基于纹理区域自适应代价计算。测试图像选择Middlebury 2006数据集中的4 组立体图像对(Aloe、Baby1、Cloth3 和Wood1)分别在不同的光照、曝光条件和无失真的条件下进行实验,并且不进行代价聚合和后处理,实验结果图像如图5~图7 所示。表2~4 分别为不同代价函数在不同的光照、曝光条件和无失真的条件下的4组图像的误匹配率,表中Avg为平均误匹配率。
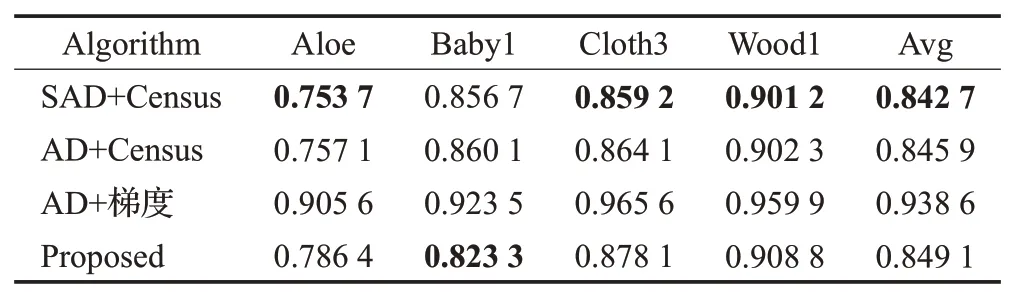
表2 不同代价函数在不同光照下的误匹配率Table 2 Mismatch rate of different cost functions under different illumination

图5 Aloe、Baby1和Wood1在不同光照下不同代价函数视差图Fig.5 Parallax diagram of different cost functions of Aloe,Baby1 and Wood1 under different illumination

图6 Aloe、Baby1和Wood1在不同曝光下不同代价函数视差图Fig.6 Parallax diagrams of different cost functions of Aloe,Baby1 and Wood1 under different exposures

图7 Aloe、Baby1和Wood1在无失真下不同代价函数视差图Fig.7 Parallax diagram of different cost functions of Aloe,Baby1 and Wood1 without distortion
从表2到表4中,可以看出SAD和Census结合的代价函数与AD和Census结合的代价函数在不同光照、不同曝光和无失真情况下的误匹配率相当,且相较于AD和梯度相结合的算法,误匹配率下降16.55%,所以本文提出的代价函数在强纹理区域选择AD 和Census 结合的代价函数计算代价;同时对于表4 中的弱纹理图像Wood1,AD 和梯度相结合的算法相较于SAD 和Census结合的代价函数以及AD 和Census 结合的代价函数而言,误匹配率下降5.33%,所以在弱纹理和无纹理区域,本文选择AD 和梯度结合的代价函数计算代价;由表2和表3可知,梯度受到光照和曝光等外部因素的影响很大,由实验结果可知,本文所提出的代价函数不仅能够适用于强纹理区域,而且在弱纹理和无纹理区域也有很好的鲁棒性,能够适用于多种复杂的外部环境。
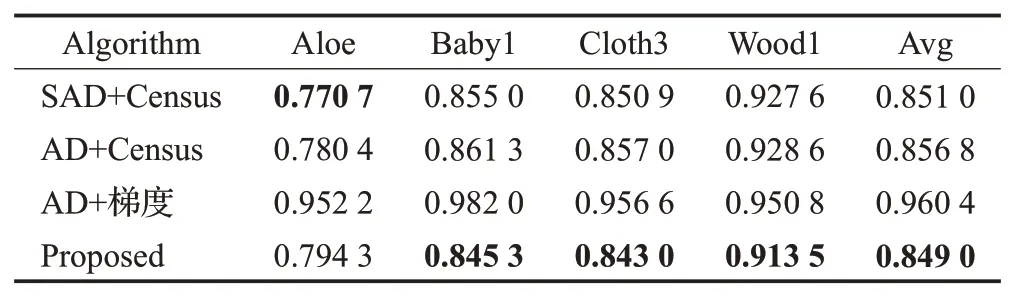
表3 不同代价函数在不同曝光下的误匹配率Table 3 Mismatch rates of different cost functions under different exposures

表4 不同代价函数在无失真下的误匹配率Table 4 Mismatch rates of different cost functions without distortion
2.2 代价聚合算法验证
为了验证本文所提出的十字臂构建策略在代价聚合中的有效性,本文选择Middlebury数据集作为测试图像,实验均采用相同的代价计算函数,且都不进行视差后处理。实验对比了本文算法及SAD+Census、AD+Census、SGM[10]、IGF[16]、ADSR_CIF[17]、LESC[18]和ELAS[19]算法,实验结果见图8 所示,与传统SAD+Census、AD+Census 和SGM 算法相比,所提算法在弱纹理和无纹理区域取得更加精确的匹配效果;同时与IGF、ADSR_CIF和ELAS算法相比,所提算法在丰富纹理图像上的匹配精度更高,但前者在视差不连续区域匹配精度更高,与适应性最好的LESC 匹配效果相当,但所提算法更简单,能应用于实时匹配。由表5 数据可知,本文算法相较于其他算法中效果次好的ELAS算法,误匹配率下降了3.57个百分点,相较于LESC算法,实时性相对更强。由于在弱纹理和无纹理区域所包含的像素点更多,所以聚合后的视差更能接近真实视差值;在代价聚合后,可以进行视差后处理步骤,能够进一步提高最终视差图的匹配精度,最终,Cones、Teddy、Wood2、Cloth3、Rock2、Plastic、Aloe和Baby1图像经过后处理优化后,误匹配率分别为12.04%、13.34%、12.86%、9.15%、11.84%、12.58%、10.94%和12.16%。
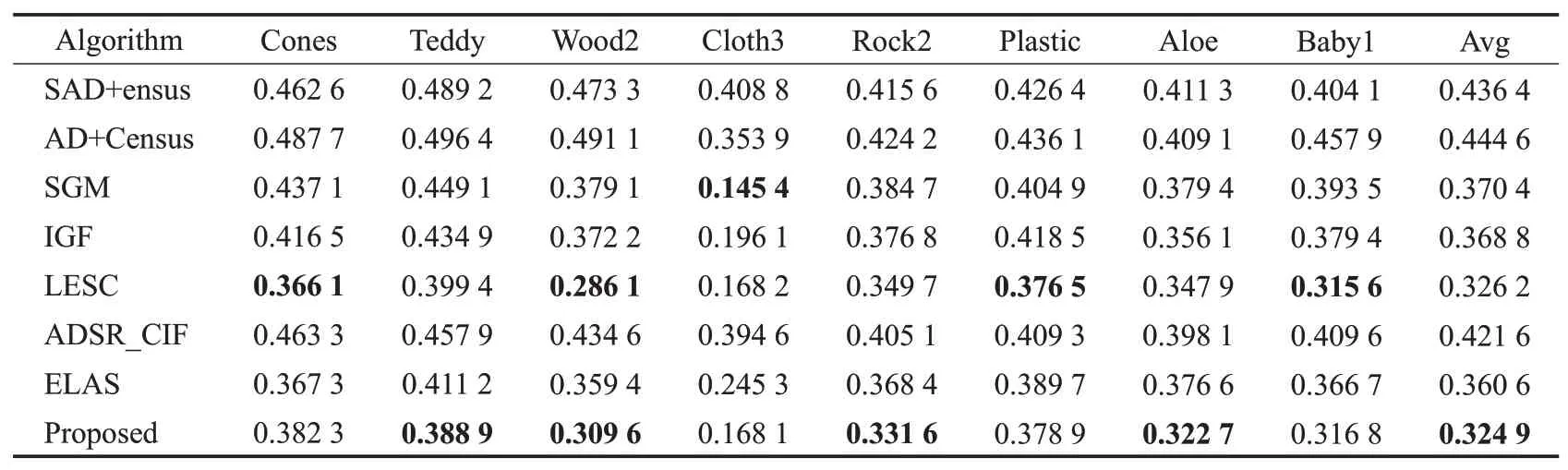
表5 所提算法与其他算法聚合后的误匹配率Table 5 Error matching rate after aggregation of proposed algorithm and other algorithms

图8 不同立体匹配算法聚合后视差图Fig.8 Parallax map after aggregation of different stereo matching algorithms
3 参数分析
为了分析不同的参数对实验结果的影响,对实验过程中的9个主要参数进行分析,本算法在纹理区域判断的阈值τ设为4(即四个方向的像素点差值都设置为1)。立体匹配图像选用Middlebury 2003 数据集中的Cones和Teddy,实验结果如图9所示。其中,参数λGrad、λCensus和λAD是匹配代价计算中的三个主要参数,而参数L1和L2以及t1~t4都是代价聚合过程中的主要参数。由不同参数实验匹配精度结果可知,由(a)知参数λGrad在60之后的匹配精度无明显变化,故取值为60;由(b)知,随着λCensus值的递增,误匹配率在不断上升,由曲线Cones可见,在30 时取到最小值,但曲线Teddy 上则是不断递增,故为综合两曲线,取值为20;由(c)知λAD对两条曲线的误匹配率影响趋势不同,且曲线Cones 在150 之后趋势变缓,故取值为150;由(d)知随着L1递增,误匹配率在不断上升,且对于曲线Teddy,在26~28之间有一个突变下降,故综合两条曲线,取值为28;由(e)知L2对两条曲线的影响不同,对Cones 无显著影响,对Teddy 而言,随着L2递增,误匹配率不断上升,故最终取值为13;由(f)知随着t1递增,两条曲线的误匹配率都在不断下降,故取值为24;由(g)知t2对两条曲线的影响不相同,且曲线Cones在t2取7后,误匹配率无显著变化,故取值为7;由(h)知参数t3对曲线Cones 而言,除了在开始不断下降外,总体上都是无明显变化,故取值为250;由(i)知随着t4递增,两条曲线误匹配率不断上升,故取值为1,将所有参数设置为上述分析的值后,可以获得精度更好的视差图。

图9 不同参数实验结果图Fig.9 Experimental results of different parameters
4 结束语
文章提出了一种自适应纹理区域的多尺度融合立体匹配算法,在代价计算阶段,首先划分出强纹理、弱纹理和无纹理区域,再在强纹理区域采用AD和Census相结合的代价函数,在弱纹理和无纹理区域采用AD和梯度相结合的代价函数,使得本文提出的代价函数能够适应不同纹理区域,并取得相当好的匹配精度;在代价聚合阶段,在强纹理区域采用颜色和空间距离相结合的十字臂支持域构建条件,在弱纹理和无纹理区域采用梯度和空间距离结合的构建条件,与传统的CBCA构建方法相比,本文提出的构建方法能够适应不同的纹理区域,且在弱纹理和无纹理区域能够包含更多的像素点,得到更长的臂长。实验选择不同光照、不同曝光和无失真三种情况,对比不同代价函数的匹配精度,从而构建出此算法的代价函数;同时再对比此算法和其他七种主流算法在代价聚合后的匹配精度,实验结果表明,此算法较于ELAS,最终平均误匹配率下降3.57个百分点,相较于LESC,实时性更强;最后经过参数分析后,得到对于此算法匹配效果较好的参数取值,提高算法的稳健性,能够较好地适应不同的场景,但此算法在视差不连续区域的匹配精度还有待提高,今后将进一步进行研究。

