多尺度时空特征聚合的全参考视频质量评价

张 威，赵世灵，刘银豪，王鸿奎，殷海兵

杭州电子科技大学通信工程学院，杭州310000

随着移动多媒体设备的普及，人们对高质量视频的需求与日俱增。但是在有限的带宽条件下，视频数据的压缩和传输不可避免地会导致视频质量下降。因此，设备端需要精确地评估视频质量，为调整编解码器的相关参数[1]提供参考依据。而主观视频质量评估需要组织观测者给出视频质量得分，在工业生产中并不适用，这促使研究人员寻求能与人类视觉系统（human vision system，HVS）感知一致的客观计算方法。

在早期阶段，研究者们迁移图像质量评估（image quality assessment，IQA）的知识来预测视频质量，通过对视频中所有帧的质量进行简单的时域平均池化得到视频质量得分。虽然此类方法实现简单且时间复杂度低，但由于缺少针对视频中复杂的时域特征建模[2]，其预测结果与实际人类主观感知结果仍有一定差距。

时间尺度是视频的重要特征，在过去几年间，研究者花费大量精力分析如何把时域信息应用于视频质量评价。在TLVQM 中，Korhonen 等[3]从小时间尺度的角度出发，逐帧分析运动光流与时域失真的关系，通过统计光流的变化来测量视频中的运动失真。随后，Liu等[4]提出FAST，每次间隔9 帧对视频序列提取固定长度的运动轨迹，在较大的时间尺度下，比较失真视频与原视频间运动内容的差异来描述运动轨迹的失真。近年来随着卷积神经网络的运用，研究者们也试图利用深度学习的方法解决视频质量评价存在的问题。在Kim等[5]提出的DeepVQA中，通过提取HVS的时空敏感度图来预测单帧质量，并利用敏感度图对视频帧进行加权获得视频质量。在C3DVQA中，Xu等[6]引入2D卷积网络和3D卷积网络相结合的方法学习时空特征，通过对大量的特征进行聚合回归得到预测得分。在Liu等的SDM[7]中重新对FAST 进行优化，通过卷积神经网络对光流信息进行二次特征提取与降维，并引入注意力机制预测视频质量。

然而这些基于传统特征[3-4]或基于深度学习[5-7]的全参考视频质量评价方法（full-referenc video quality assessment，FR-VQA），普遍都是在固定时间尺度下对视频进行处理。小时间尺度下提取的细粒度时空特征尽管具有较高的分辨率，但是对全局信息的刻画能力不足。而大时间尺度下提取的粗粒度时空特征虽能更快速感知视频整体内容，但却不能对局部场景详细描述。根据反向层次理论[8]（reverse hierarchy theory，RHT），视觉神经将眼睛捕捉的图像传输到外侧膝状核，后者通过前馈连接将信息传递到由V1 区域到V5 区域组成的视觉皮质，在高级皮层对全局场景建模；而高层皮质区域（V2、V3、V4、V5）还存在到低层皮质区域（如V1）的反馈连接，由大脑引导眼球转动对局部细节感知。因此，建立一个能够有效聚合多尺度时空域特征的预测模型对于视频质量评价至关重要。

针对现有FR-VQA方法存在的问题，本文提出多尺度时空域特征聚合网络（multi-scale temporal feature aggregation network，MTN）。首先，依据HVS连续性依赖机制[9]（serial dependence in visual perception，SDP）中观测者更关注失真片段的特性，模型自适应采样失真明显的片段；其次，模型结合长短时记忆网络[10]（long short-term memory network，LSTM），通过多个LSTM网络层堆叠增加网络感受野，进而感知多时间步长的采样片段，提取各个尺度的时域上下文特征。为探索如何对多尺度特征有效聚合，本文模拟大脑正反向多次迭代感知的过程，通过在多个记忆网络层之间建立连接，以前馈与反馈串联的路径对多粒度的时域上下文信息进行聚合；最后，引入多通道自注意力机制对各时间尺度的视频序列分别进行预测，视频质量得分由不同时间尺度下预测得分的均值构成。

1 多尺度时空域特征聚合网络

如图1所示，本文所提的视频质量评价算法主要包括自适应采样模块及信息聚合模块两部分。首先，输入视频数据至自适应采样模块，SDM 中关于连续性依赖机制实验[7]已证明感知过程中最差感知质量帧会造成更显著影响，故自适应采样模块明确选择失真较为明显的帧进行着重分析。

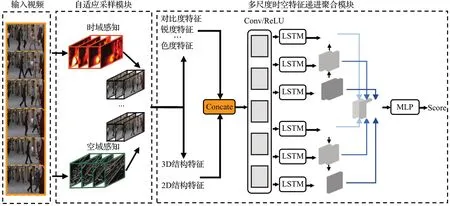
图1 多尺度时空域特征聚合模型总框图Fig.1 Overall structure of proposed multi-scale spatiotemporal feature aggregation model

其次，本文结合循环神经网络（recurrent neural network，RNN）在时间序列方面展现出的强大建模能力，利用堆叠的LSTM 网络提取多时间尺度下的时空依赖特征。最后，本文依据视觉神经研究中的反向层次理论探究对多尺度特征的有效融合方式，尝试刻画与人类感知相符的聚合方法。

1.1 基于感知依赖机制的自适应采样策略

现有FR-VQA 模型提取高层次的时空域特征时往往需要大量计算。为降低算法复杂度，模型大多会通过采样策略对视频数据进行筛选。而固定间隔采样策略能够保持数据分布的均匀性且使用简单，已有VQA 算法普遍都采用此策略。

然而最近的视觉神经研究已经证明人眼感知过程中存在连续性依赖机制[9]，当受测者受到视频信号刺激时，大脑总是试图使用先前的视觉感知信息来指导对当前视觉输入的感知。SDM中的实验进而证明受测者对视频的观看体验更易受到视频中失真严重帧所造成的影响。但是固定间隔采样却忽视此感知特性，直接从视频序列中按照固定步长采样若干帧，这无疑会丢失部分具有显著影响的失真帧，进而导致VQA 模型预测准确度的降低。

为准确衡量视频中逐帧的感知失真进而对序列进行采样，与自然图像的空域失真相比，视频中的图像还受到时域掩蔽效应影响。本文考虑到当相邻帧间出现较剧烈的运动时，由于运动掩蔽效应[11]，人眼聚焦能力迅速下降，运动模糊隐藏部分失真。为充分刻画运动掩蔽效应对空域失真的影响，本文受到MOVIE[12]中处理时空域掩蔽方法的启发，首先利用帧间运动剧烈程度FMT(t)的倒数表征运动掩蔽效应的强弱FAT(t)；其次依据当前时刻运动掩蔽的程度对空域失真FQS(t)做加权处理；最后本文提出感知运动失真度指标（perceived motion distortion，PMD）来描述第t帧在运动情况下的失真程度。

视频质量感知是一个复杂的过程，视觉系统可以被视为由不同皮质区域组成多层次结构，其中纹外皮质的连续皮质层MT/V5 在运动知觉中发挥重要作用，皮质层上的大量神经元具有空间频率和方向选择性，对沿特定方向移动的刺激反应最强烈。因此，为充分刻画帧间运动程度的指标FMT( )t，模型需要同时对运动强度与运动方向进行描述。参考感知运动能量[13]的计算方法，视频帧被划分为N块不重叠48×48 大小的宏块，并用宏块级运动矢量幅度的均值表示当前帧的运动强度，其中mi,j(t)是指是第t时刻帧i,j位置宏块的运动矢量幅度。通过计算视频帧的光流直方图HOF(t,k)，得到在第t时刻分布在k角度范围内的光流幅度，而帧内运动矢量的主导运动方向θ由幅度最大的光流决定。统计所有方向光流得到第t帧的主导运动方向本文将2π划分为n个角度，n的大小与FAST中的参数设定一致，设置为8。定义帧间运动程度FMT(t)为帧级运动强度与主导运动方向乘积：

N()⋅表示归一化操作，运动程度FMT( )t被线性归一化在0-1之间。当FMT( )t =0 时，表示该帧的内容保持静止状态；当FMT( )t =1 时，表示帧内运动程度最为剧烈。图2 分别展示视频序列中处于不同时刻帧内的运动矢量方向与感知运动能量分布。

图2 CSIQ数据集中名为“Basketball”失真视频的若干帧Fig.2 Frames of distorted video named“Basketball”inCSIQ dataset

与许多其他VQA算法类似，本文也使用现有的IQA算法来测量逐帧空域失真FQS(t)。权衡算法复杂度与测量精确度，模型使用图像结构失真度[14（]gradient magnitude similarity deviation，GMSD）衡量视频信号中t时刻帧的空域失真程度。GMS为图中N个块的梯度幅度差异，而GMSM为帧内GMS的均值：

为确保分母非零，取γ值为1 的常数，当FMT(t)+γ=1 时，表示前后帧间没有运动，此时感知失真程度为FQS(t)；当FMT(t)+γ大于1 时，表示相邻帧间存在运动掩蔽效性而隐藏部分噪声，此时感知失真程度应小于FQS(t)。

受测者观看视频时，只能感知到较短时间内的若干帧。普通视频帧率约为30，而大脑并不能在1/30 s内对每帧做出反应[15]。因此合理假设视觉感知数目为T帧的视频片段。为确保采样数据分布均衡，本文将序列平均切分成N段T帧的子视频段，依据SDM 与FAST 进行参数设置，视频段数N=10，帧长度T=18。考虑到失真总是分布于连续的若干帧中，所以在每段子视频中确定最大PMD 指标帧所在的位置，从该位置往两端延伸T/2 个连续帧作为具有显著影响片段，图3展示自适应采样与固定间隔采样数据分布差异。

图3 固定间隔采样与自适应采样结果对比图Fig.3 Difference between fixed interval frame sampling and adaptively frame sampling

图3中蓝色曲线为感知运动失真度PMD，越大的PMD 指标表明感知失真越严重。红色与紫色线段对应的x轴坐标分别为固定间隔与自适应采样得到的视频帧索引。以SDM中使用的固定间隔采样策略[7]为例，每隔7帧采样一段长度为18帧的视频片段，由于忽略HVS更关注严重失真帧的特点，所以图3（a）中标出的红色填充区间丢失对失真严重帧的选取。而自适应采样考虑失真帧总会造成更显著影响，图3（b）中所标注的紫色填充区间可以发现，在每个视频片段中都能取到最大PMD指标的帧。

1.2 多尺度时空域特征递进聚合网络

多尺度信息是时间序列建模过程中所需的关键要素。而大多数现有方法只利用单一时间尺度时空域特征对每个序列样本进行表征，这忽略了各样本间内容的差异性。本文为此专门设计了多尺度特征迭代递进网络，整个框架如图4所示。

图4 多尺度特征迭代递进网络Fig.4 Architecture of multi-scale feature progressive network

直观来说，对于场景切换较多的视频，其内容需要较小尺度的LSTM网络来捕捉短期依赖，而对于场景切换较少的视频，则需要更大的尺度来捕捉长期依赖。因此，只提取单个固定尺度的时空特征并不足以刻画数据集中具有不同内容的视频序列，而本文提出的特征聚合模块能够对序列提取多个时间尺度的语义特征，通过多通道注意力网络对各尺度特征进行拟合。

为追求合理的算法复杂性，本文结合HVS 感知特性，选择每段子视频中失真最严重帧作为代表帧，用以描述对应视频段的空域失真分布。而提取代表帧空域特征可以通过卷积网络感知深层语义或基于统计特性人为设计。考虑到在小数据集上大量的语义特征极易造成模型过拟合，而传统手工特征[3]具有复杂度低，鲁棒性强的优点。故本文提取饱和度特征γsat、块效应特征γblo、锐度特征γsha、对比度特征γcon和噪声特征γnoi来描述代表帧的空域信息，通过串联拼接得到N个空域特征图St。分析数据集中的视频可知，测试序列的内容大多为用户拍摄实际场景的短视频，通常只包含2~3个场景切换，故并不需要过多粒度的特征对视频感知。因此，对空域特征图St只进行3 种时间步长{α1,α2,α3}的采样，得到αi粒度的空域特征分布Sαit；并利用堆叠的LSTM网络对进行感知得到时域感知特征图，以Lαi代表采样颗粒度为αi的LSTM层；其中空域采样粒度与时域采样粒度保持一致被设置成{0，2，4}。

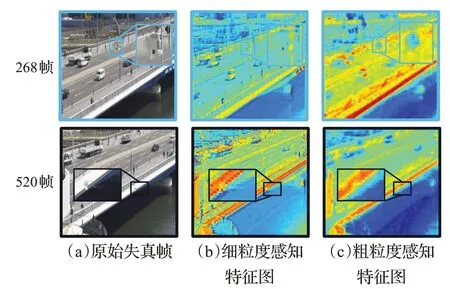
图5 CSIQ数据集中名为“BQTerrace”失真视频Fig.5 Frames of distorted video named“BQTerrace”in CSIQ dataset

图5（b）为小时间尺度下提取的细粒度特征图，帧内局部纹理凸显；图5（c）为大时间尺度提取的粗粒度特征图，侧重对帧的全局信息进行刻画。

以下公式中h′为网络隐藏层的初始状态，默认各项设置为0.1。其中F()⋅、δ()⋅、A()⋅分别表示全连接层、ReLu激活层、平均池化层，代表第t段子视频的预测得分。

在过去的研究中，通常使用时域的平均池化来拟合预测得分，这忽略HVS 感知机制的影响。而自注意力机制能够学习各段视频之间的相关性，保留各视频段的上下文关系。故引入多通道的自注意力网络，关注感知最差时刻神经网络所提取语义特征，将完整视频的语义特征表示为，通过缩放点积的方法比较与Hαi中每段视频特征分布的相似性，进而自适应的完成权重分配，其中dh为隐藏层的大小。

经过对多尺度的序列内容感知，提取丰富时间语义特征，拟合每一段视频的预测得分，完整视频的预测得分可以表示为。利用多通道的自注意力机制对各段视频进行比较，得到自适应权重Wαi=最终视频的得分Q表示为不同时间尺度下预测得分的均值：

2 实验结果与分析

为保证实验的有效性，本文在香港中文大学图像与视频处理实验室提供的IVPL 数据集以及广泛使用的LIVE与CSIQ[16]数据集分别进行实验。数据集具体信息如表1所示。

表1 数据集信息Table 1 Information of dataset

本文遵循与主流文献一致的测试流程，随机选择80%的参考视频进行训练，剩下的20%用于验证。一旦某个参考视频被划分到训练集或测试集，由它生成的所有失真视频将被放入对应的数据集中，以保证训练集与测试集之间没有交集。在随机划分数据集重复实验10次的条件下，使用斯皮尔曼等级相关系数（Spearman’s correlation coefficient，SRCC）、肯德尔等级相关系数（Kendall’s tau coefficient，KRCC）和皮尔逊线性相关系数（Pearson correlation coefficient，PLCC）进行性能比较。

（1）PLCC 用于衡量预测得分Ypre与主观评分Xlab之间的线性相关程度，令∂Xlab与∂Ypre分别为其标准差，通过cov()⋅计算其协方差，则PLCC可以表示为：

PLCC的取值范围为[0，1]，该数值越大表示预测结果与实际主观评分线性相关程度越强，模型预测越准确。

（2）SRCC 和KRCC 用于衡量预测得分与主观得分间的等级相关性，取n为数据对的总数，di为预测得分与主观得分间的等级差异，nd为得分不一致的数据对数，ns为得分一致的数据对数。这两者可以表示为：

SRCC 与KRCC 的取值范围为[]-1,+1 ，当预测值与标签值的变化趋势完全相同时，这两个变量之间的相关系数可以达到+1；若两个变量的变化趋势完全相反，则相关系数达到-1。对于VQA 问题，SRCC 或KRCC越接近+1，代表模型效果越好。

2.1 模型性能比较

为全面地比较本算法，本文将所提方法与现有的10个FR-VQA模型进行比较，即PSNR、MS-SSIM[17]、GMSD、MOVIE、Vis3[16]、VMAF[18]和FAST，以及近些年提出的基于深度学习FR-VQA模型DeepVQA、C3DVQA和SDM。本文对已开源的算法按照相同的流程进行验证，性能结果以*号注明，其余模型的性能均取自相关文献。表2列出三个公开数据集上各种FR-VQA模型的总体性能。

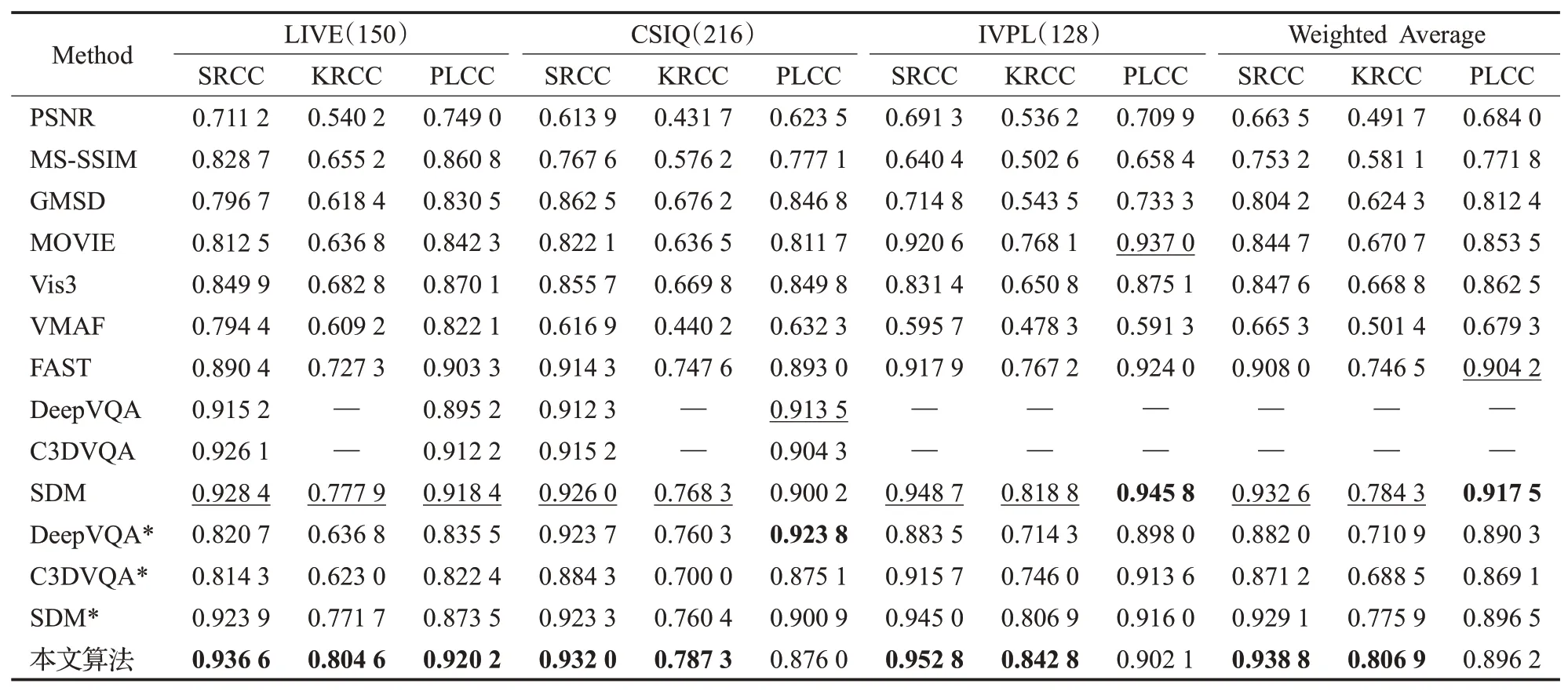
表2 VQA算法在各个数据集上的性能Table 2 Performance comparison of video quality evaluation algorithms on various dataset

通过比较SRCC、KRCC 指标可以看出：（1）传统全参考图像质量评价算法如PSNR、MS-SSIM、GMSD 忽略视频在时间域上的失真，导致算法性能表现比较差；（2）利用传统统计特征的FR-VQA 算法如MOVIE、VMAF、Vis3、FAST 等通过加入前后帧间的光流特征对时域失真表征，较IQA 算法性能有部分提升，但仍与人类主观感知有差距；（3）而基于深度学习的FR-VQA 算法如C3DVQA、DeepVQA 等总体性能较传统方法都有大幅提升，但C3DVQA 或者DeepVQA 在LIVE 数据集实测的性能并不出色，这是由于深度学习方法在传统小数据集上由于样本量少参数量多，模型极易出现过拟合，从而导致模型泛用性下降，其预测结果容易受到数据集划分的影响。此外，上述三种FR-VQA算法都采用固定间隔采样策略，并没有深入考虑将采样策略与HVS的感知特性相联系。

本文所提算法在公开数据集中绝大部分指标都取得最优或者次优的结果，且SRCC 指标都高于0.93，这表明本算法具有更强的稳定性与泛化能力，始终与人类感知保持良好的一致性。图6给出多种IQA与VQA算法的性能分布情况，橙色横线代表性能的中位数，绿色三角形代表其平均值。

图6 模型的性能结果（SRCC与PLCC）对比Fig.6 Performance comparison（SRCC and PLCC）

由箱线图可以观察到部分算法预测结果较为分散。如图6（b）中MS-SSIM 算法获得的PLCC 指标最高达到0.943 8，而最低得分却只有0.538 6，所以得分的分布范围也是比较算法的标准之一。从此角度看，在不同数据集的多个指标中，本文提出的方法不仅拥有更加优越的性能而且预测得分的分布也更加紧凑，证明该方法具有更强的有效性和鲁棒性。

视频预测得分与真实得分被归一化到0-1 范围内，预测得分越接近图7 中的对角线，表明预测精确度越高。图7中将此前性能最优算法SDM与本文算法在LIVE数据集上进行比较。从图中可以看出本算法的预测数据主要分布在对角线的两侧，展现更良好的拟合效果。

图7 模型主观得分与预测得分的分布图Fig.7 Subjective score and predicted score distribution diagram

2.2 消融实验

为充分验证算法中不同模块的有效性，本文以SRCC、KRCC、PLCC 以及RMSE 为指标在三个公开数据集中进行消融实验，分别对固定间隔采样模块（fixed interval frame sampling module，FFS）、自适应采样模块（adaptively frame sampling，AFS）、多尺度时域信息融合模块及多通道自注意力模块进行增量实验，比较各模块对性能的影响。

如表3所示，随着各个模块的加入绝大部分指标都有提升。例如LIVE 数据集中，初始仅利用固定间隔采样策略SRCC与KRCC仅为0.923 9和0.771 7，而加入本文所提出的自适应采样模块，模型对严重帧失真进行感知，SRCC与KRCC指标略有提升；再接入多尺度感知网络感知时序特征，SRCC与KRCC指标显著提升到0.936 4与0.802 3；最后接入多通道的注意力机制对时序特征回归，得到预测得分，虽然SRCC 与KRCC 提升较小但是PLCC 提升显著，由此验证注意力机制对于模型预测准确性的提升。虽然LIVE数据集中多模块的组合在每项指标都取得最好成绩，但在CSIQ 数据集中PLCC 与RMSE却有所损失，原因为其视频帧率在25~60 之间不等，三种尺度感知特征并不具有完整代表意义，进而影响模型性能。本文以SRCC为指标，对引入的模块在三个数据集中进行增量实验，实验结果在柱形图8中进行展示。

表3 不同模块在各个数据集上的性能比较Table 3 Performance comparison of different modules on various dataset

图8 不同数据集下，不同模块组合的性能结果对比Fig.8 Comparison of results of different modules combinations on various dataset

实验结果证明，AFS+MTN+MTA的组合在CSIQ数据集中实测所得PLCC与RMSE指标虽并未取得最优，但综合考虑其他数据集中的多项指标表现来看，其仍取得最优的性能。

对帧内空域特征进行刻画时，为比较基于神经网络提取的深度特征与人为设计的传统特征在性能和复杂度的区别，本文在仅改变空域特征提取方式的条件下，以SRCC 为指标测试完整模型在各数据集的性能表现以及模型前向推理耗费的时间。其中，深度特征的提取方式与CNN-TLVQM[19]一致，利用预训练的ResNet-50网络对视频帧进行感知得到深度特征图Srest，而传统手工特征以字符Strat表示。针对不同分辨率视频，CPU上的测试结果以秒为最小时间单位统计。具体结果如表4所示，其中{XXX}frs@{YYY}p分别表示视频包含帧数以及视频分辨率。

表4 不同特征提取方式耗费时间对比Table 4 Comparison of time taken by different feature extraction methods单位：s

为验证基于深度学习的特征图Srest与利用传统手工特征拼接特征图Strat的有效性，本文在多个公开数据集以SRCC为指标进行对比实验，最终结果如表5所示，并在图9中展示多次实验所得分数的分布范围。

表5 各数据集中不同特征提取方式性能对比Table 5 Performance comparison of different feature extraction methodson various dataset

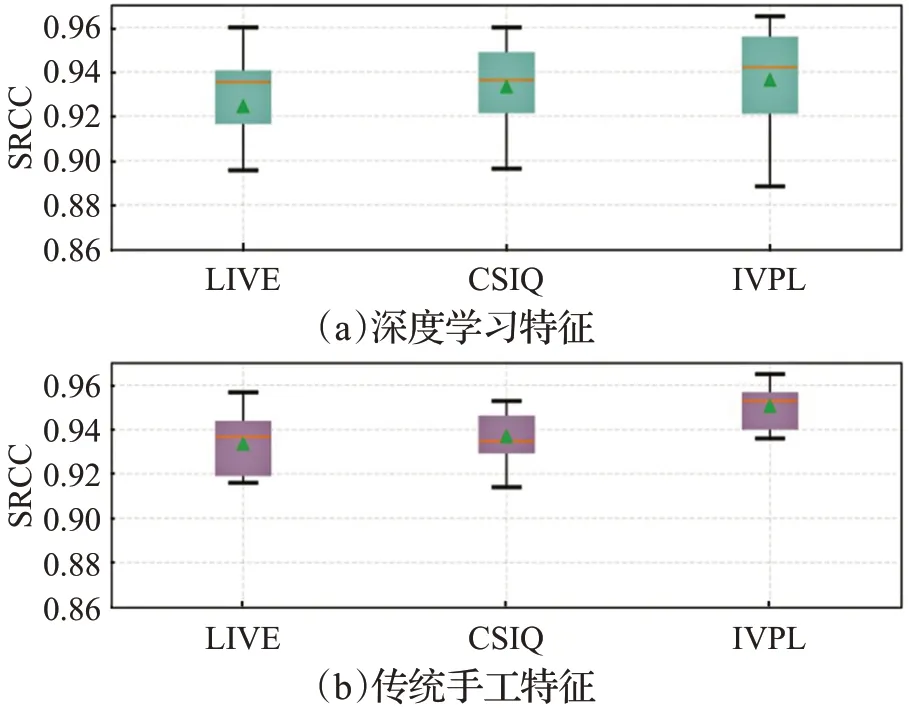
图9 各数据集中不同特征提取方式性能对比Fig.9 Performance comparison of different feature extraction combinations on various dataset

由图9 可知基于深度学习的特征与基于统计特性的传统手工特征在各数据集上性能相差并不大，但是神经网络模型计算复杂度较高，特征提取耗费时间较长，而传统手工特征拥有更低计算复杂度。此外，利用传统手工特征得到的实验结果上下浮动较小且下限较高，而利用深度学习特征得到的实验结果差异较大。这主要因为预训练的神经网络模型包含上百万的参数，而全参考数据集较小极容易得到过拟合的特征图，导致模型的鲁棒性下降。

3 结论

首先，本文结合感知失真度与感知连续机制提出自适应采样策略，成功克服传统方法中固定间隔采样丢失关键帧的弊端；其次，为解决单一尺度特征对视频整体失真刻画不充分的问题，本文从HVS 的长期记忆机制出发，利用堆叠的LSTM 网络提取多尺度的时空域特征，并结合人类视觉复杂的前反馈感知机制，进而探究聚合多尺度特征的有效方式，提出基于多尺度时空特征聚合网络的全参考视频质量评价算法。通过全面的消融实验，验证了所提各模块的有效性。在多个公开数据集的实验结果表明，本文模型具有更优的泛化能力，且与人类感知基本一致，相对于目前最优FR-VQA方法表现出更出色的性能。