利用halo导航星的地月空间联合自主轨道确定
刘 磊,刘 也,程 潏,刘 勇
(1. 北京航天飞行控制中心航天飞行动力学技术重点实验室,北京 100094;2. 北京跟踪与通信技术研究所,北京 100094;3. 北京邮电大学自动化学院,北京 100876)
0 引 言
作为人类开发宇宙和星际移民的前哨,地月空间目前受到高度关注,主要航天大国均制定了面向未来地月空间开发的探测计划,如美国正在实施“阿尔忒弥斯”(Artemis)重返月球计划,着力打造可以自由往返地月空间以及前往火星的“门户”空间站[1]。中国于2020年底成功实现月球采样返回,此前已完成了日地和地月平动点飞行、小行星飞越探测、月球背面着陆探测等创新性任务[2-4],目前正在开展月球探测四期工程任务,后续将建设国际月球科研站,并积极推进载人登月任务。同时,有学者提出了开发利用地月空间的“地月空间经济区”概念,涉及航班化地月空间运输体系、空间资源探测与开发体系和空间基础设施体系等[5]。后续这些地月空间开发和利用中涉及大量地月往返、交会对接、着陆、对接等飞行任务,由此引发对导航定位的强烈需求。月球和深空探测任务的导航定位,当前依赖于地面测控网,其优点在于地面计算处理能力较强,可以采用多种类型测量手段以确保精度和可靠性,缺点在于需要建立分布广泛的地面观测台站,同时,深空探测任务通信延迟较大,某些特殊操控需求难以及时响应,任务长期运行也会造成地面测控资源紧张、人员工作负荷大等问题。随着星载设备性能的提高,可以有效缓解上述问题的空间自主导航定位技术得以充分发展和逐步应用。
目前,月球和深空探测任务的自主导航定位方法主要有惯性导航、视觉导航和天文导航[6-9],综合精度、性能和可靠性而言,卫星导航应是地月空间自主导航定位的首选手段。但是,常见的地球卫星导航系统,一方面受限于距离难以支持月球或深空探测器的导航定位,另一方面若采用传统的星星跟踪测量手段,导航卫星与用户星联合定轨时存在秩亏问题造成绝对位置无法解算[10]。2005年,Hill[11-12]提出了联合星际卫星自主导航(LiAISON)概念,在三体引力场中实现了仅利用星间测量的绝对定位[13-14],从而有效解决了上述问题,引起了广泛关注。基于LiAISON技术,Parker等[15-16]研究了环月卫星的导航问题,将地面站数量从6个减少为3个且有效提高了导航性能,Fujimoto等[17]研究了GEO卫星的导航,Zhang等[18]研究了地月L1、L2、L4和L5星座的导航性能,Turan等[19-20]研究了地月L2卫星与环月椭圆冻结轨道之间的导航,以及地月小卫星编队的自主轨道确定性能,Wang等[21]研究了DRO与地球轨道、地月转移轨道和环月轨道的导航,Gao等[22]研究了地月halo轨道与DRO轨道的导航,王丹丹[23]和杜兰等[24]研究了基于月球平动点轨道的自主定轨,Zhang等[25]研究了平动点导航星座的性能,熊欢欢[26]研究了平动点卫星与地球导航卫星联合自主定轨。这些工作从导航星和用户星轨道类型、测量数据类型、测量误差等方面,较为全面地研究了LiAISON导航技术在不同应用场景和条件下的性能,有力推动了该技术在未来任务中的潜在应用。2022年6月28日发射的美国Artemis任务验证星CAPSTONE前往地月NRHO轨道与环月卫星LRO开展LiAISON导航技术验证[27],从而将该技术推向实际应用。因此,LiAISON有望成为未来地月空间自主导航定位的主要技术手段。
从研究现状可见,作为研究对象的用户星集中于地心或者月心轨道,对于地月空间任务的重要轨道类型——地月转移轨道涉及非常少。为此,文章面向未来地月空间任务的自主导航定位需求,研究了地月halo导航星和地月空间卫星的联合自主定轨,建立了联合自主定轨模型,讨论了定轨系统的可观性,其中,导航星位于地月平动点halo轨道。为了研究和对比地月halo导航星对地月空间任务典型轨道的支撑能力,用户星轨道包括低地球轨道(LEO)、地月转移轨道(CTT)、环月低轨道(LLO),重点分析不同误差条件下的联合自主定轨精度,为LiAISON技术在后续月球和深空探测任务中的应用提供技术支撑。
1 联合自主定轨模型
LiAISON利用导航星和用户星的星间测量(SST)数据进行联合定轨解算[11-14]。在利用SST的轨道确定方面,美国于20世纪60年代考虑利用GEO卫星作为跟踪站,Vonbun于1967年提出利用同步卫星与其他卫星的星间测量数据进行轨道确定,分析了利用GEO卫星ATS-6和GEOS-3与NIMBUS-6卫星的星间测量定轨精度[28-29]。理论上,SST可以提供导航星和用户星轨道的大小、形状和相对方位信息,但是二体轨道的绝对方位并不唯一,需要地基测量配合才能实现自主定轨。否则,要求其中一颗卫星的轨道大小、形状和空间方位必须唯一,空间中的太阳辐射压、非对称引力场、第三体引力均可使得轨道满足上述要求,因此,LiAISON通过将一颗卫星放置于非对称引力场下的平动点轨道,利用导航星和用户星间的SST测量数据,联合解算二者运动以实现自主定轨,SST数据类型可以为距离、距离变化率或角度,或者同时使用多种数据以实现自主定轨。
采用SST进行地月halo导航星和用户星的联合自主轨道确定如图1所示。

图1 地月空间卫星联合自主定轨Fig.1 LAOD of satellites in the cislunar space
设地月会合坐标系中,地月halo导航星和用户星的位置向量分别为rs和ru,二者之间的距离ρ为
ρ=||ru-rs||=
(1)
设自主定轨的状态量X为
(2)
可得非线性状态方程
(3)
(4)
(5)
于是,可得方程的雅克比矩阵A(t)为
(6)
式中:03,I3和03×6依次为三维全0矩阵、三维单位矩阵、3行6列的0矩阵。
进而,线性化式(3)得到状态方程
ΔX=Φ(t,t0)ΔX0
(7)
式中:ΔX0和ΔX分别为初始时刻t0和时刻t的状态偏差,Φ(t,t0)为t0至t的状态转移矩阵,可根据式(6)求解[30]。
以ρ作为测量量Y,得测量方程
ΔY=HΔX
(8)
式中:观测矩阵H为
(9)
其中,01×3为三维全0行向量。
考虑测距误差和卫星初始轨道误差,且设二者均为零均值正态分布随机误差,其中,测距标准差为σρ,用户星和导航星的初始轨道误差相同,位置和速度标准差分别为σsp和σsv。因此,测量噪声R和初始协方差阵P0为
(10)
(11)
状态噪声阵的位置和速度分量根据试算分别取10-20和10-26。基于状态方程和测量方程,采用最小二乘批处理或者扩展卡尔曼滤波(EKF)方法[30],可以实现对导航星和用户星运动状态的联合估计,其中滤波方法可以满足实时或近实时处理需求。
2 联合自主定轨可观性
halo导航星与用户星联合自主定轨的可行性涉及到系统可观性问题,即需要状态方程和测量方程组成的系统完全可观,也即利用时刻t之前的观测量可以唯一确定轨道。
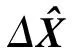
(12)
式中:权矩阵W为各测量噪声方差的倒数组成的对角阵。
式中的矩阵Λ即定轨系统的信息阵,只有Λ正定时,系统才完全可观[14,30-31]。因此,可利用Λ的正定性判断系统可观性,从而确定自主定轨的可行性。根据Λ的定义,若观测矩阵H满秩,则可以保证Λ的正定性。
为了衡量系统的定轨性能,利用Λ的条件数作为定轨系统的可观测度η
η=lg[cond(Λ)]
(13)
理论上,η数值越大,系统对误差越敏感,相应定轨性能越差。实际应用中,最终定轨精度受系统可观性和测量误差等因素共同影响,针对不同测量误差条件进行数值分析,可以获取精确量化结果。
3 数值分析
3.1 仿真条件
设地月导航星位于地月L2点北族halo轨道,幅值Az约29 000 km,导航星轨道在白道面上的投影与地月连线存在2个交点,定义距离地心较近的交点处轨道相位为0°,另一个交点的轨道相位为180°。若只利用1颗导航星,设其初始轨道相位为0°,若利用2颗导航星,则从实际应用考虑,设第2个导航星的初始轨道相位为180°,且为了降低任务成本和复杂程度,将2颗导航星布设于同一halo轨道。
用户星的LEO和LLO分别为地心和月心圆轨道,CTT转移时间Δt为5天,各颗星的升交点赤经可根据用户需要设定,轨道参数如表1所示。

表1 用户星轨道参数Table 1 Orbit parameters of the user satellites
取典型误差组合如表2所示,其中σsp取“1 000/10 000”的情况,前者为LEO和LLO的初始位置误差,后者为CTT的初始位置误差。

表2 测量误差和初始轨道误差Table 2 Errors of measurement and the initial orbit of the navigation and user satellites
导航星对LEO和LLO的连续观测时长为1天,对CTT的连续观测时长为5天,测量间隔均为60 s。采用蒙特卡洛方法进行自主定轨分析,各个误差组合均仿真100次,统计全部仿真结果的平均值作为用户星和导航星的联合定轨位置误差ΔRus和ΔRns。
3.2 可观性分析


表3 联合自主定轨系统可观性Table 3 Observability of linked autonomous orbit determination
由表3可见,三种情况下的观测矩阵均满秩,说明定轨系统可观,可以利用halo导航星与各用户星联合自主定轨。在可观测度上,导航星与LEO组合的可观测度最低,与CTT组合则最高,说明导航星与LEO联合自主定轨性能最好,与CTT联合自主定轨结果相对较差。
3.3 单导航星定轨精度
(1)halo-LEO
在仅利用单颗halo导航星的情况下,导航星与LEO的联合自主定轨结果如图2所示,图中数字表示误差组合的序号,相应曲线即该误差组合下的定轨结果。同时,给出各个采样时刻的定轨位置误差统计如表4所示。

表4 halo-LEO联合自主定轨位置误差统计Table 4 Average position errors of the halo-LEO LAOD

图2 halo-LEO联合自主定轨结果Fig.2 Results of the halo-LEO LAOD
由图2和表4可见,LEO的定轨误差明显小于导航星,前者基本优于50 m,后者基本可优于400 m。
至于测量误差和初始轨道误差的影响,首先,最大误差组合8的结果显然最差,最小误差组合1的结果最好,这符合直观认识,后续所有仿真也与此相同,不再赘述。其次,重点分析误差组合2~7对定轨结果的影响。对于LEO,误差组合2和3结果较好(9 h后均优于10 m),组合4~7稍差(9 h后均优于40 m),其中组合6在初始阶段最差;对于halo,误差组合2结果最好(9 h后均优于100 m),组合3、5和6的结果稍差(9 h后优于300 m),组合4和7结果相对最差(9 h后优于500 m)。
上述结果表明,测量误差是LEO和halo定轨误差的主要影响因素,对LEO的影响尤其明显。初始轨道误差是重要的影响因素,其中导航星初始位置误差对其定轨结果影响较大。
此外,尝试了两个地心圆轨道之间的测距自主定轨,定轨结果差于上述结果。
(2)halo-CTT
在仅利用单颗halo导航星的情况下,导航星与CTT的联合自主定轨结果如图3所示,由于误差组合4和8明显大于其他结果,为了清晰起见,图3中略去相应结果。各个采样时刻的定轨位置误差统计如表5所示。

表5 halo-CTT联合自主定轨位置误差统计Table 5 Average position errors of the halo-CTT LAOD
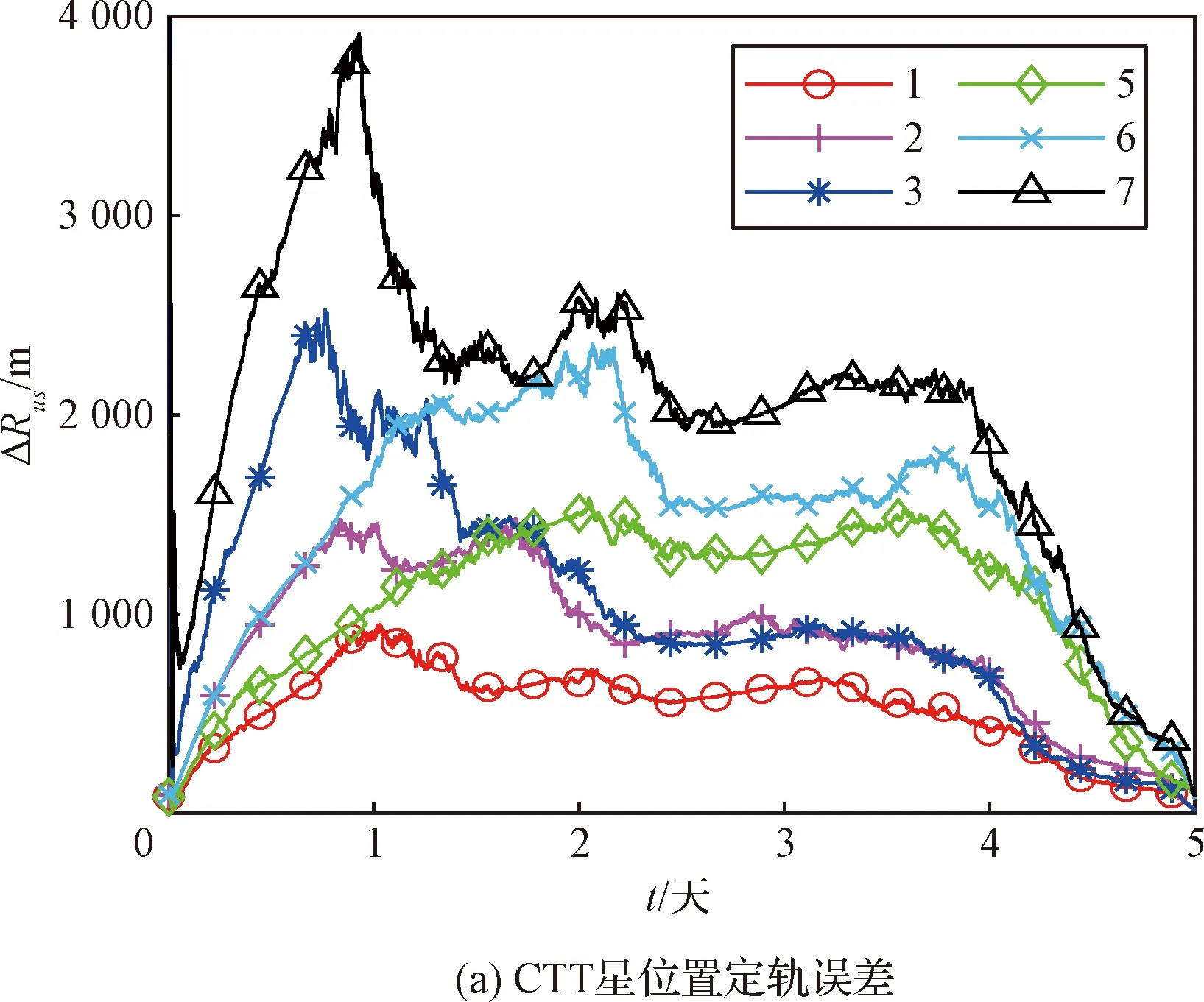
图3 halo-CTT联合自主定轨结果Fig.3 Results of the halo-CTT LAOD
由图3和表5可见,导航星的定轨误差小于CTT,虽然二者最终定轨结果相当,但是绝大多数时间内后者基本为前者的3~4倍。至于测量误差和初始轨道误差的影响,各误差组合对CTT和halo的定轨结果影响大致相同,误差组合2和3的结果较好且二者比较接近,误差组合5~7的结果较差,且6和7的结果较为近似。
上述结果表明,测量误差是CTT和halo定轨误差的主要影响因素,且影响程度明显大于初始轨道误差,除非初始轨道误差过大导致结果较差,如误差组合4。
此外,将定轨结果与初始轨道误差相比,仅在误差组合3和7下整个飞行过程中CTT的轨道精度有所改善,但是导航星的轨道精度在误差组合3、4、7和8下均得到明显提高,其他误差组合的结果与初始误差也在同一量级,说明halo-CTT联合自主定轨对导航星的价值高于用户星。
(3)halo-LLO
在仅利用单颗halo导航星的情况下,导航星与LLO的联合自主定轨结果如图4所示,各个采样时刻的定轨位置误差统计如表6所示。

表6 halo-LLO联合自主定轨位置误差统计Table 6 Average position errors of the halo-LLO LAOD

图4 halo-LLO联合自主定轨结果Fig.4 Results of the halo-LLO LAOD
由图4和表6可见,LLO的定轨误差明显小于导航星,前者基本优于50 m,后者则为前者10倍以上。至于测量误差和初始轨道误差的影响,各误差组合对LLO和halo的定轨结果影响不同,对于LEO,误差组合2、3和5结果较好(9 h后均优于30 m,最终优于10 m),组合6和7稍差(9 h后优于40 m,但是变化较大),组合4的结果最终接近组合8;对于halo,误差组合2和5结果最好(9 h后优于200 m),误差组合3、6和7的结果稍差(9 h后优于500 m,最终优于300 m),误差组合4结果最终与组合8近似。
上述结果表明,测量误差是LLO和halo定轨误差的主要影响因素,初始轨道误差是重要的影响因素,较大的初始轨道误差会极大程度地削弱高精度测量的作用。
综合对比三种用户星的自主定轨结果可见,同等误差下LEO定轨精度最高,LLO次之,CTT最差,这与3.2小节可观性分析结论完全一致。
3.4 双导航星定轨精度
从3.2小节结果可见,LEO和LLO类型的用户星均可以利用单颗halo导航星进行自主定轨,且可以在较短时间内大幅降低初始轨道误差。相比之下,CTT类型的用户星则难以借助单颗halo导航星改善其轨道精度。
针对上述问题,考虑增加1颗halo导航星,即利用2颗halo导航星与CTT用户星联合自主定轨,研究导航星数量对CTT轨道确定的作用,观测时长、频率、误差等条件与前述单颗导航星完全相同。
在2颗halo导航星的情况下,首先分析自主定轨系统的可观性和可观测度,结果表明系统可观,且可观测度参数η降低至15.675,说明自主定轨性能相对单颗halo导航星有明显改善。
导航星与CTT的联合自主定轨结果如图5所示,各个采样时刻的定轨位置误差统计如表7所示。由于第2颗导航星的定轨结果与第1颗较为接近,限于篇幅,图5和表7中略去相应结果。

表7 双导航星的halo-CTT联合自主定轨位置误差统计Table 7 Average position errors of the halo-CTT LAOD with two halo satellites

图5 双导航星的halo-CTT联合自主定轨结果Fig.5 Results of the halo-CTT LAOD with two halo satellites
由图5和表7可见,导航星的定轨误差与CTT大致相当,前者略优。至于测量误差和初始轨道误差的影响,误差组合2和5的结果较好(优于300 m),组合3、6和7的结果稍差(优于1 000 m),组合4的结果较差。该结果表明,双导航星测量条件下,测量误差和初始轨道误差对CTT和halo定轨误差的影响程度相当。
将定轨结果与初始轨道误差相比,各种误差组合的定轨结果均可以保持在初始轨道误差相同的量级,或者有较大程度改善。
此外,将双导航星联合定轨结果与单导航星相比,无论是用户星还是导航星,轨道精度均提高2倍以上,尤其是最大误差组合8的结果可以实现全程优于初始轨道,说明用户星和导航星均可受益于halo-CTT联合自主定轨。
4 结 论
文章研究了利用halo导航星的地月空间联合自主轨道确定,研究结果表明,利用地月halo导航星可以实现与地月空间卫星的联合自主定轨。综合对比地心轨道、地月转移轨道与月心轨道的自主定轨结果可见,在单颗halo导航星条件下,地心和月心轨道的定轨精度最高,halo导航星次之,地月转移轨道最差。但是,若增加1颗halo导航星,地月转移轨道的定轨精度可以提高2倍以上。同时,测量误差和初始轨道误差对不同用户星的联合自主定轨影响不同。
文中用户星轨道涵盖了地月空间任务的主要轨道类型,不过具体任务存在不同特征飞行阶段,如月面下降和上升、交会对接等,平动点导航星对于这些任务的自主定轨支持能力需开展进一步研究。此外,地月空间三体轨道类型丰富,选择其他类型的三体周期轨道作为导航星轨道对导航性能的影响,以及估值方法和测量手段的合理选择等,将是后续研究方向。

