风电机组载荷优化对变桨轴承力学行为影响研究*

顾光成,刘 勇,叶 锋,虞亚杰,蒋丹青,刘继鑫,陈家杰,施恒荣

(1.国电宁波风电开发有限公司,浙江 宁波 315000;2.浙江运达风电股份有限公司,浙江 杭州 310000;3.浙江省风力发电技术重点实验室,浙江 杭州 310000)

0 引 言

变速变桨风电机组通常采用PID控制器进行桨距角控制,但由于风速的大范围性及随机性,固定参数的PID控制器并不能满足所有风况场景的需求。在复杂场址高湍流以及极限阵风的影响下,风电机组变桨过程中会不可避免地产生载荷冲击,加大部件的可靠性风险。因此,为降低机组关键部位的载荷,实现载荷优化目标[1],需要在变桨控制时采用自适应的动态PI参数,以提高变桨系统响应,且需要机组根据外部风速波动以及发电机转速等参数动态调整变桨参数。

变桨轴承作为联接风电机组叶片与轮毂的关键部件,受载荷优化的直接影响,其可靠性对整机运行安全性与稳定性至关重要[2,3]。

得益于有限元分析(finite element analysis, FEA)技术的发展,研究人员可以对受载时变桨轴承的力学响应进行更为全面准确的计算分析[4]。近年来,很多学者对变桨轴承力学性能进行了研究。

OLAVE M等人[5]提出了一种基于FEA的四点接触回转支承轴承设计方法,突破了早期通用轴承设计采用的工程计算方法中,对轴承套圈及周边联接件所做的刚性假设。汪超等人[6]运用ANSYS软件构建了变桨轴承局部模型,并借此分析了轴承的最大载荷。SMOLNICKI T等人[7]应用试验和FEA方法,研究了大型轴承的载荷分布特性。郑辉等人[8]采用Newton-Raphson方法,计算了变桨轴承在外载荷作用下的变形情况,并应用FEA方法对其进行了准确度验证。田志亮等人[9,10]分别建立了考虑安装结构的变桨轴承有限元模型,研究了变桨轴承强度和套圈翘曲与椭圆变形对载荷分布的影响。庞健华等人[11]应用FEA方法,对变桨轴承套圈应力和疲劳强度进行了分析,并改进了设计,提高了轴承可靠性。张禄[12]建立了变桨轴承FEA模型及疲劳寿命计算公式,对多种可能影响变桨轴承疲劳寿命的因素进行了详细分析。何先照等人[13]基于在线测试与FEA方法,对风电机组运行过程中变桨轴承的动态柔性特性进行了研究。

以上这些研究主要关注的是变桨轴承本身的力学性能与设计改进,在载荷变化对变桨轴承力学行为影响规律方面,则缺乏系统性研究,以致难以定量预测载荷优化对变桨轴承可靠性提升产生的影响,不利于变桨控制策略的准确制定。

针对上述问题,笔者采取了以下措施:1)引入在线测试技术,实时测量某MW级风电机组载荷优化前后不同功率下的载荷与对应的变桨轴承内外套圈的相对位移,从而获得载荷优化对变桨轴承变形影响程度的实测数据;2)应用FEA方法构建变桨轴承系统有限元模型,使用实测载荷数据作为输入进行仿真计算,并对比载荷优化前后变桨轴承内外套圈相对位移的仿真解与实测数据,以验证并总结载荷优化下变桨轴承变形程度的变化规律。

此外,笔者应用FEA方法,计算并定量分析载荷优化对变桨轴承滚动体与滚道间接触应力、滚道边缘接触余量角的影响。

1 在线测试方案

1.1 载荷测试方案

风载作用于风电机组叶片后,经由叶根传递至变桨轴承,因此,变桨轴承所受载荷的主要组成为叶根位置的挥舞与摆振弯矩。根据IEC 61400-13标准[14],笔者可以采用在叶根处安装T型全桥应变片的方式对叶根弯矩载荷进行测量。

载荷测试方案如图1所示。

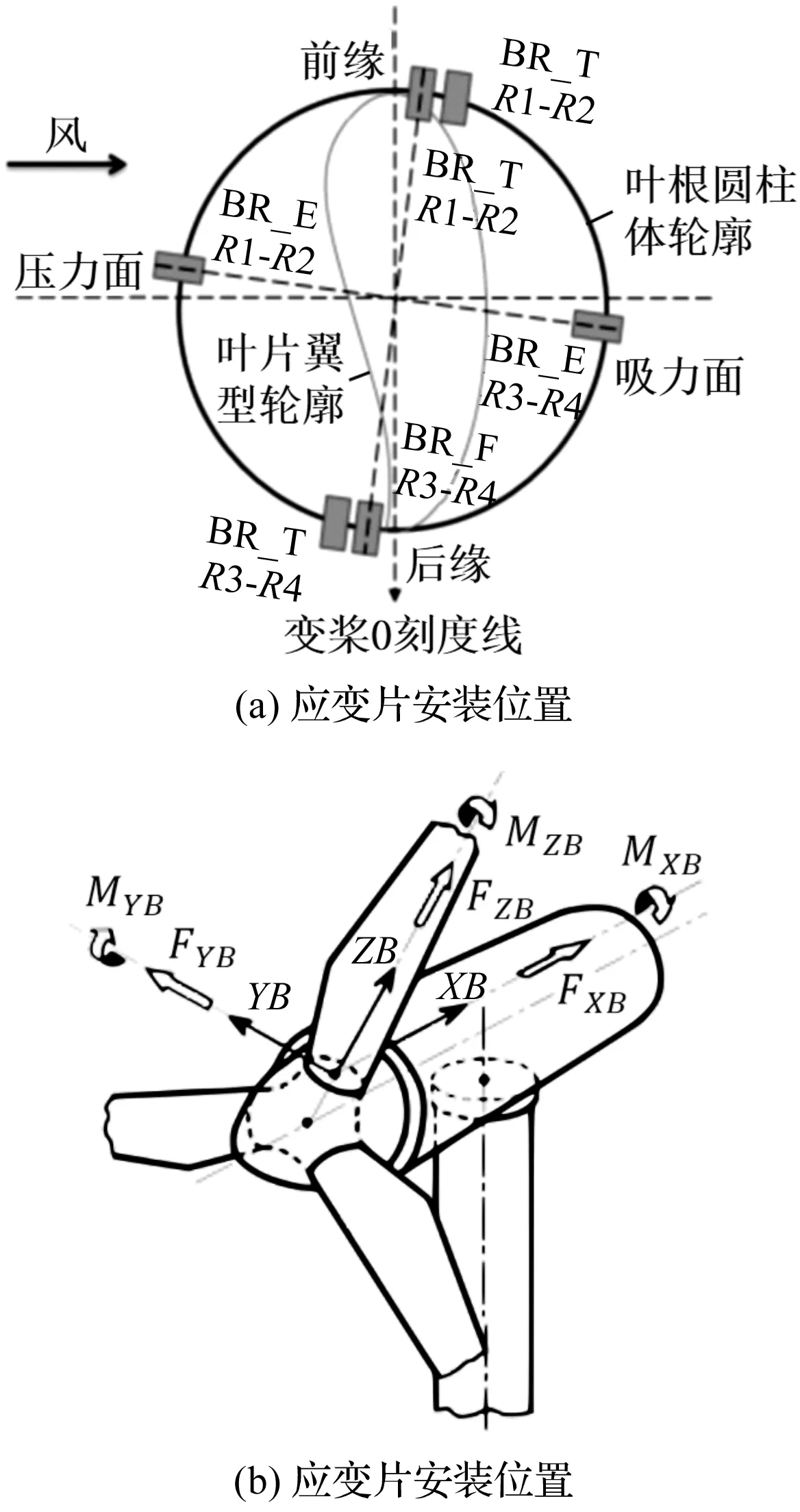
图1 载荷测试方案示意图

笔者在所关注的变桨轴承对应叶根的挥舞和摆振方向各安装2组HBM K-CXY3-0060-1-350-O应变片,进行弯矩测量。其中,应变片安装于叶根圆柱体四等分位置,距离叶根螺栓最深处0.5 m处,如图1(a)所示。

按照图1(b)所示,载荷坐标系实时测量载荷优化前后不同发电功率水平下的叶根弯矩MXB和MYB,其中,XB、YB分别为叶片的挥舞与摆振方向。

1.2 变桨轴承内外套圈相对位移测试方案

变桨轴承受叶根弯矩作用后会发生变形,变形程度可由内外套圈的轴向与径向相对位移进行表征。

变桨轴承内外套圈相对位移测试方案如图2所示。

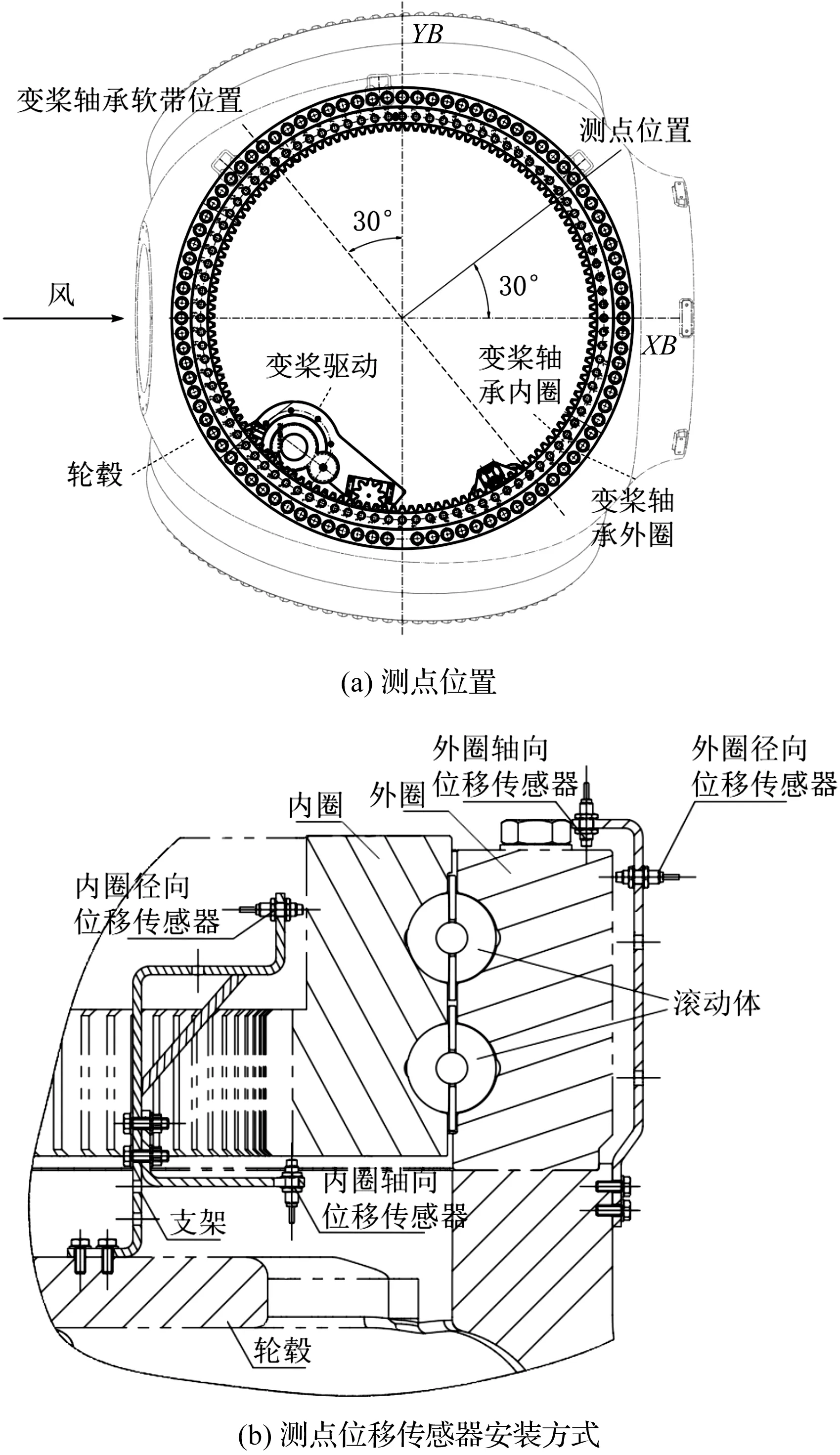
图2 变桨轴承内外套圈相对位移测试方案示意图

该研究中,变桨轴承的设计软带位置(即经验受载最小位置)在与YB夹角为30°的位置,且与之垂直,即与XB夹角为30°的位置为经验受载最大位置,其对应的受载后变桨轴承变形也最大。

笔者设置测点位置如图2(a)所示,根据风电机组设计经验,该位置的变桨轴承承受载荷最大,所产生的较大变形可方便笔者进行测试,且在此处安装测试设备不会对变桨驱动产生干涉。

按照图2(b)所示方式,笔者在测点位置将4个BAW004T电感式测距传感器安装在固定于轮毂的支架上,分别测量变桨轴承内外套圈测点相对于对应传感器的轴向与径向位移。轮毂相对于变桨轴承可视为固定不动的参照物,经换算可得到上述测量数据测点位置内外套圈的轴向与径向相对位移。

综上所述,笔者根据在线测量载荷优化前后不同功率水平下的叶根弯矩MXB和MYB,及对应的变桨轴承套圈轴向与径向相对位移,即可获得用以分析载荷优化对变桨轴承变形程度影响的实测数据。

2 仿真分析方法

2.1 有限元模型

笔者使用FEA方法对变桨轴承系统进行仿真分析,变桨轴承系统有限元模型如图3所示。

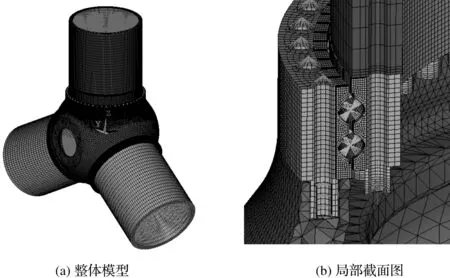
图3 变桨轴承系统有限元模型

笔者建立的模型包含了“叶根-轴承-轮毂”装配体,且考虑了变桨轴承自身及其周边支撑结构的柔性影响。其中,叶根部分包括桨叶假体与叶根法兰,均使用六面体实体单元进行建模;轮毂使用四面体实体单元进行建模;叶根与变桨轴承内圈、轮毂与变桨轴承外圈使用螺栓进行联接,其中的螺母使用六面体实体单元进行建模,螺杆及刚性联接使用梁单元进行建模;变桨轴承为四点接触球轴承结构,包括内外套圈与上下滚道滚动体,其中套圈使用六面体实体单元进行建模,滚动体使用刚性杆单元及承拉不承压的单向弹簧单元简化建模,该方法可用于有效分析轴承受载后包括滚道与滚动体间接触载荷与接触角等在内的力学响应[15]。

以单个滚动体为例,其简化建模方法如图4所示。

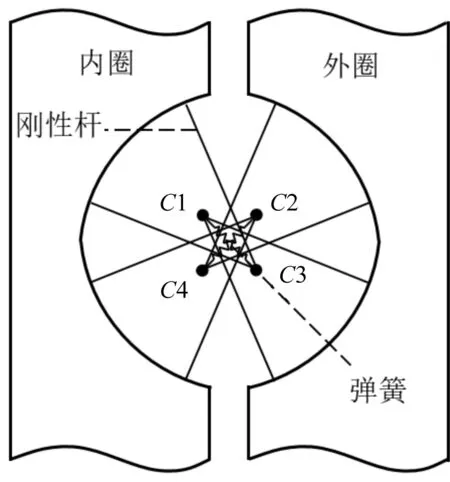
图4 变桨轴承滚动体简化建模示意图

图4中,C1、C2、C3、C4分别为外圈下滚道、内圈下滚道、内圈上滚道及外圈上滚道表面曲率中心。笔者使用刚性杆单元联接滚道表面节点及其对应的滚道曲率中心点,并使用承拉不承压的单向弹簧单元分别联接C1与C3、C2与C4。

为模拟滚动体与滚道接触时的载荷非线性传递特性,笔者使用Hertz接触理论,根据轴承几何参数及材料性能计算接触载荷与接触点的位移关系[16],并将该关系以“载荷-变形”曲线的形式作为非线性刚度属性赋予弹簧单元,如图5所示。

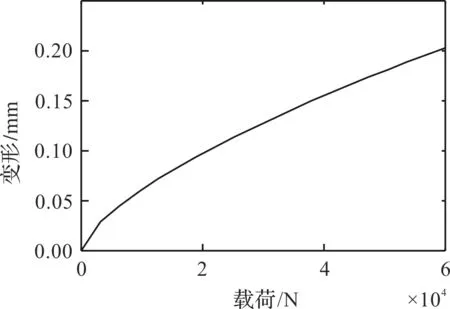
图5 弹簧单元“载荷-变形”曲线

仿真分析中,弹簧单元所产生的拉力即为接触载荷,弹簧单元与变桨轴承滚道节圆平面间的夹角即为滚动体与滚道间接触角。

2.2 有限元分析内容

笔者使用2.1节中描述的变桨轴承系统有限元模型,将1.1节中描述的在线测试方案所获得的实测叶根载荷作为计算输入,开展多方面的仿真分析研究,具体如下:

1)变桨轴承内外套圈相对位移

参照图2所示的在线测试方案,笔者在有限元模型中4个位移传感器所对应的测点位置设置节点;从有限元分析结果中提取各节点的轴向与径向位移解,经换算即可得到测点位置内外套圈的轴向与径向相对位移的仿真解;

2)滚动体与滚道间最大Hertz接触应力

根据文献[17],四点接触球轴承静承载安全系数SF表达式如下:

(1)

式中:Smax为滚动体与滚道间最大Hertz接触应力。

由式(1)可知,SF与Smax的三次方成反比关系,Smax对变桨轴承可靠性至关重要。

滚动体与滚道间的接触载荷及Hertz接触应力为变桨轴承内部力学响应,无法采用物理试验手段直接测量。如2.1节所述,笔者使用弹簧单元模拟滚动体的力学性能。在仿真分析中,变桨轴承受载后各弹簧单元的轴向拉力解即为对应滚动体与滚道间的接触载荷,由此可根据Hertz接触理论进一步计算出相应的Hertz接触应力,提取其中的最大值即为Smax。具体计算方法参见文献[16];

3)滚动体与滚道间最小边缘接触余量角

根据Hertz接触理论,变桨轴承受载后,滚动体与滚道发生接触时形成接触椭圆斑[18]。HARRIS T A[19]指出,轴承运行中应避免出现接触椭圆被滚道边缘截断的情况,否则可能造成边缘应力集中及不良润滑,从而影响轴承可靠性。针对这一可靠性要求,笔者提出了滚动体与滚道间边缘接触余量角的概念。

此处以单个滚动体为例,其相关角度定义如图6所示。

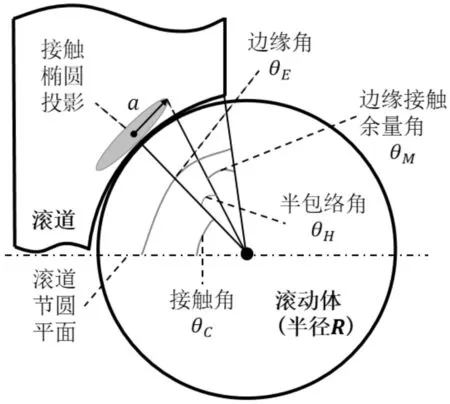
图6 变桨轴承接触相关角度定义示意图

笔者将接触椭圆投影中心至球心线段与滚道节圆平面间的夹角定义为接触角θC;以滚动体球心为顶点,将分别联接接触椭圆长轴边缘与接触椭圆中心所形成线段间的夹角定义为半包络角θH;将滚道边缘至球心连线与滚道节圆平面间的夹角定义为边缘角θE。

则边缘接触余量角θM定义如下:

θM=θE-(θC+θH)

(2)

式(2)中,角度变量均存在于变桨轴承内部,在变桨轴承受载情况下,难以采用物理试验手段直接测量相关角度变量。

在仿真分析中,笔者根据滚道边缘及滚动体球心(即弹簧单元中心)坐标求出θE;根据弹簧单元两端节点坐标求出弹簧单元与滚道节圆平面间的夹角,即θC。

θH计算如下:

(3)

式中:a为接触椭圆长半轴长度;R为滚动体半径。

根据Hertz接触理论,可基于轴承设计几何参数、材料性能及接触载荷计算得到a,具体计算方法参见文献[16]。

根据上述步骤计算各滚动体对应的θM,提取其中的最小值,记为θM_min。为了避免接触椭圆截断发生,θM_min应大或等于0°;且其数值越大,安全余量越高。

3 在线测试与仿真分析结果

3.1 在线测试结果

3.1.1 载荷测试结果

在正常发电工况下,风电机组稳定运行于某一功率水平时,叶根载荷具有周期性特点,叶轮旋转一圈即为一个循环周期。

按照1.1节所描述的载荷测试方案,笔者在被测风电机组开启自适应动态PI参数变桨控制策略进行载荷优化前后,以MYB最大为原则,对发电功率为150 kW、450 kW、850 kW、1 250 kW及1 600 kW时的载荷测试数据进行周期性筛选,各功率水平下获得MXB、MYB数据约500组。

统计结果汇总如表1所示。

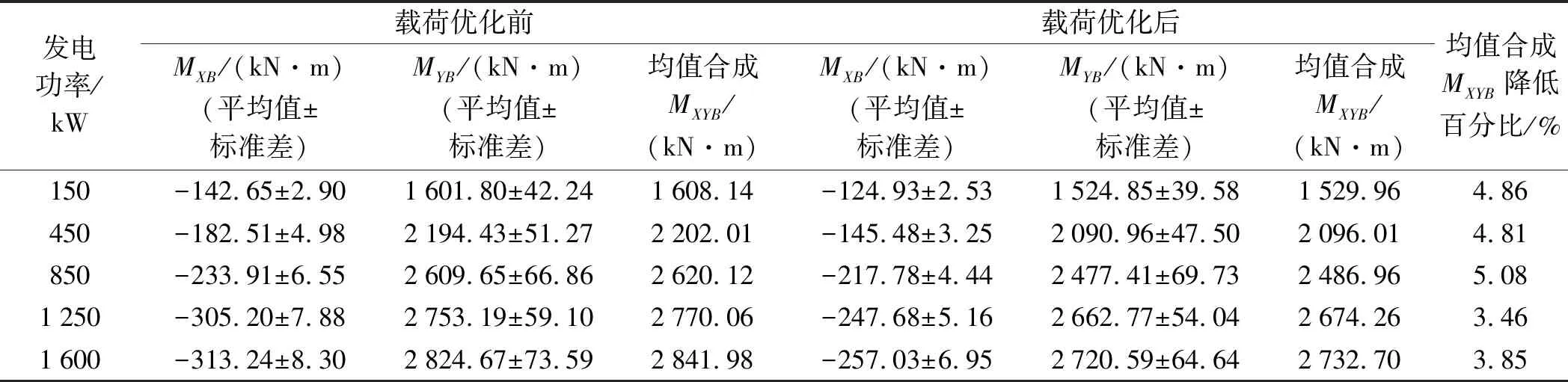
表1 载荷测试数据

根据MXB、MYB均值合成均值合弯矩MXYB可知,MXYB总体上随发电功率增大而增大。开启载荷优化控制策略后,在各功率水平下,均值MXYB可以实现3.46%～5.08%的降载效果。

3.1.2 变桨轴承内外套圈相对位移测试结果

按照1.2节所描述的变桨轴承内外套圈相对位移测试方案,笔者在载荷测试的同时提取测点位置载荷优化前后不同发电功率对应的位移传感器读数,并计算内外套圈径向与轴向相对位移。

笔者筛选出与3.1.1节所描述的载荷数据点所对应的相对位移测试数据并进行统计分析,变桨轴承内外套圈相对位移测试结果如表2所示。

表2 变桨轴承内外套圈相对位移测试结果

由表2测试结果可知:载荷优化前后变桨轴承内外套圈径向与轴向相对位移平均值随发电功率增大均呈现出增大趋势,且同功率条件下径向相对位移大于轴向相对位移;开启载荷优化控制策略,并实现降载后,各功率水平下的变桨轴承变形程度均相应减小[20,21],内外套圈径向与轴向相对位移平均值减少0.02 mm～0.05 mm。

3.2 仿真分析结果

3.2.1 变桨轴承内外套圈相对位移仿真分析结果

笔者按照第2节所描述的有限元建模方法,建立被测风机变桨轴承系统模型,以表1所示5个发电功率水平下载荷优化前后共计10组叶根载荷实测均值数据作为计算输入,进行仿真分析。

此处以载荷优化前发电功率1 600 kW工况为例,其有限元分析所得位移云图如图7所示(MXB=-313.24 kN·m,MYB=2 824.67 kN·m;变形效果放大倍数为50)。

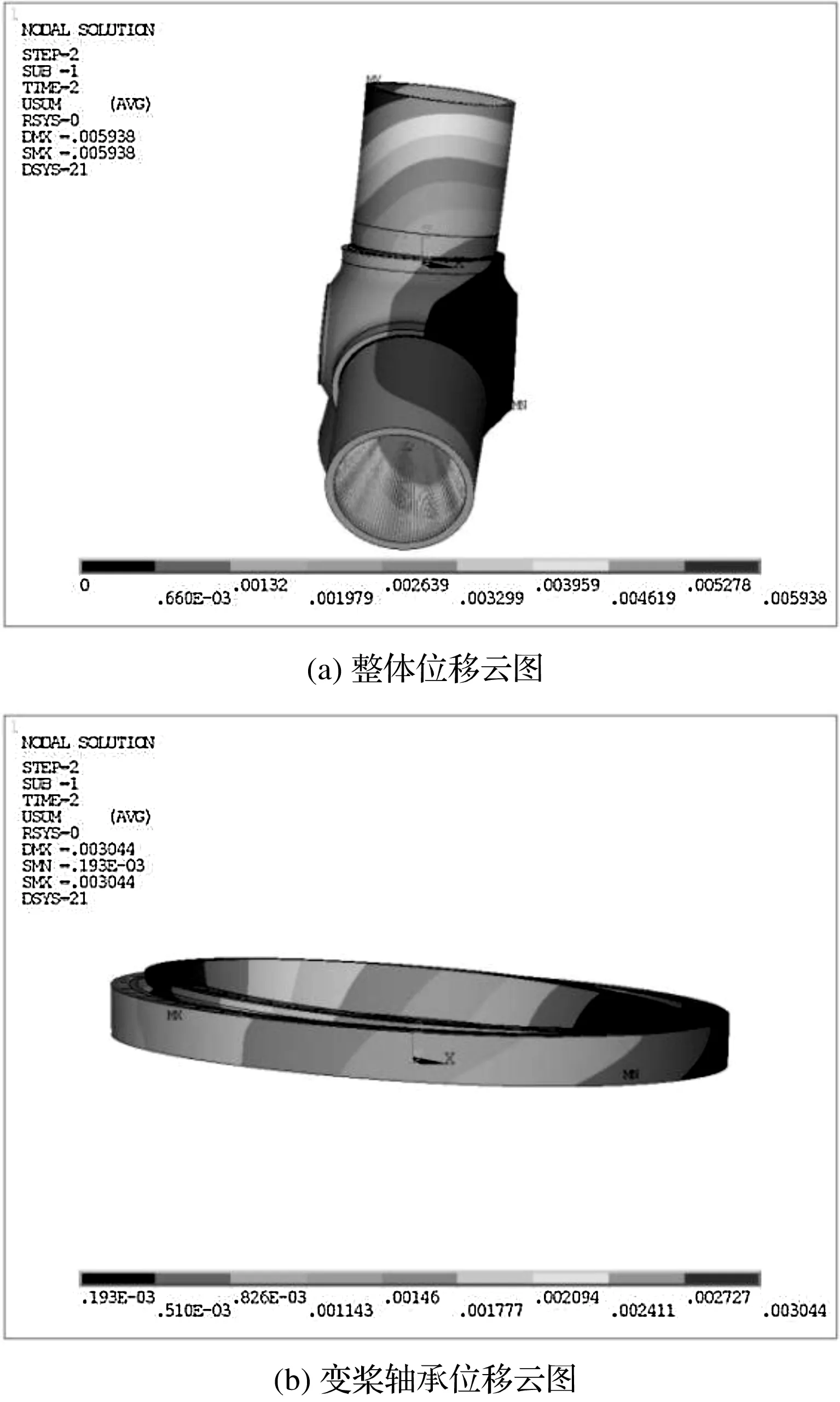
图7 仿真分析位移云图结果

笔者提取测点位置节点的位移解,即可计算出变桨轴承内外套圈径向与轴向相对位移。

全部仿真分析结果数据统计如表3所示。

表3 变桨轴承内外套圈相对位移仿真分析结果

对比表3和表2测试结果可知:同一发电功率水平下,仿真分析所得变桨轴承内外套圈径向、轴向相对位移及相对位移减少量均偏小,但处于同一量级,且规律相同:载荷优化前后,变桨轴承内外套圈径向与轴向相对位移随发电功率增大均呈现出增大趋势,且同功率条件下径向相对位移大于轴向相对位移;载荷优化后,各功率水平下变桨轴承变形程度均相应减小,内外套圈径向与轴向相对位移减少0.01 mm～0.02 mm。

由此可见,笔者所使用的仿真分析方法具备合理性,仿真分析与在线测试结果所体现的载荷优化对变桨轴承内外套圈相对位移的影响,其规律具有一致性。

3.2.2 滚动体与滚道间最大Hertz接触应力

按照2.2节所描述方法,笔者提取各工况有限元分析结果中弹簧单元的轴向拉力,即得到各滚动体与滚道间的接触载荷,进而根据Hertz接触理论计算得到Hertz接触应力,并提取最大值Smax。

相关结果数据如表4所示。

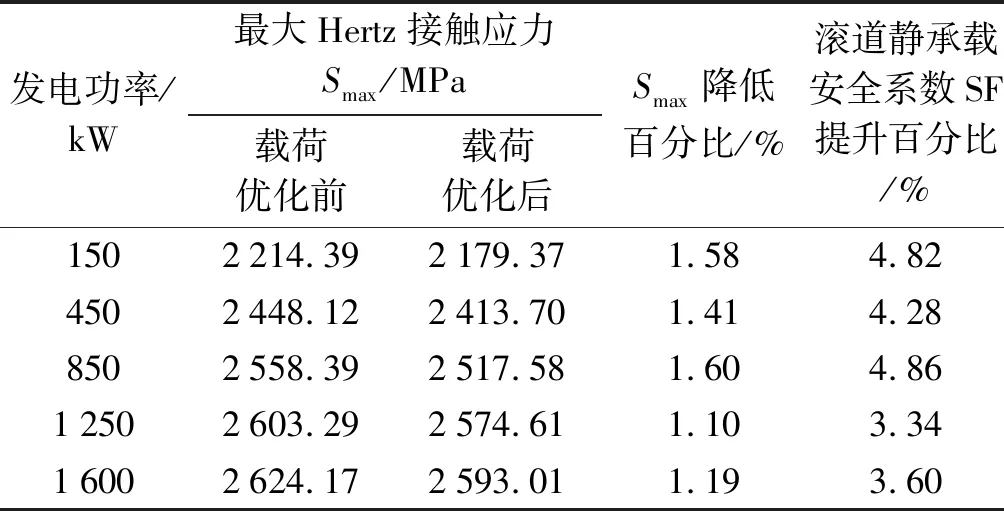
表4 变桨轴承滚动体与滚道接触相关仿真分析结果

由表4可知:在载荷优化前后,Smax随发电功率增大均呈现出增大趋势;载荷优化后,各发电功率水平下,Smax降低了1.10%～1.60%。

根据式(1)计算可得:相应的滚道静承载安全系数SF提高了3.34%～4.86%,说明滚道承载可靠性得到提高。

3.2.3 滚动体与滚道间最小边缘接触余量角

按照2.2节所描述方法及定义,笔者提取各工况有限元分析结果中变桨轴承受载后的滚动体与滚道间接触载荷、弹簧单元两端节点的位置坐标,根据变桨轴承设计固有几何参数与材料属性,基于Hertz接触理论,计算得到各滚动体与滚道间的边缘接触余量角,提取其中的最小值θM_min,并加以汇总。

滚动体与滚道间最小边缘接触余量角仿真分析结果如表5所示。

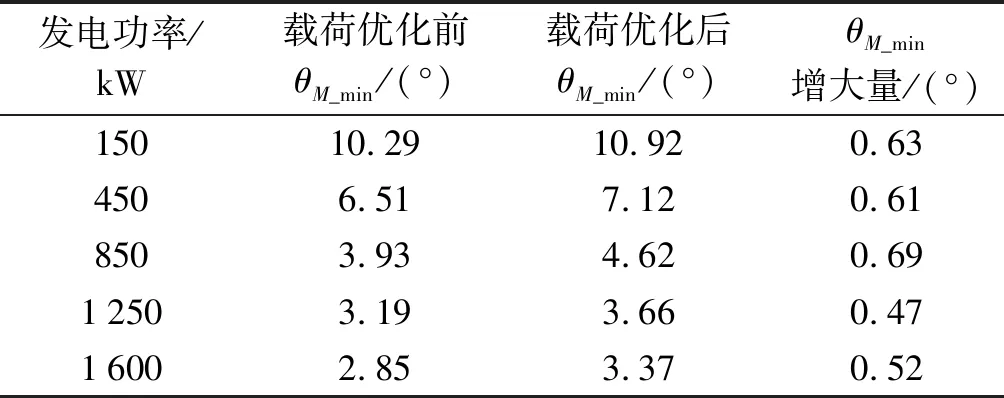
表5 滚动体与滚道间最小边缘接触余量角仿真分析结果

由表5可知:在载荷优化前后,θM_min随发电功率增大均呈现出减小趋势;各发电功率水平下,载荷优化后,θM_min增大了0.47°～0.69°,发生接触椭圆被滚道边缘截断的风险降低。

4 结束语

笔者采用在线测试方法,优化了某MW级风电机组载荷的降载效果,对变桨轴承变形的影响进行了现场测量;以实测载荷数据为输入,应用FEA方法,分析了载荷优化对变桨轴承变形、滚道与滚动体间最大Hertz接触应力及最小边缘接触余量角的影响规律。

研究结果表明:

1)在线测试结果显示,应用自适应动态PI参数变桨控制策略实现了3.46%～5.08%降载效果后,变桨轴承内外套圈径向与轴向相对位移平均值均减小了0.02 mm～0.05 mm,表明变桨轴承变形程度减小;

2)仿真分析结果同样显示载荷优化可以降低变桨轴承变形程度,其规律性与在线测试结果一致;

3)载荷优化可以降低最大Hertz接触应力达1.10%以上,从而提高了滚道静承载安全系数;

4)载荷优化可以增大最小边缘接触余量角达0.47°以上,从而减小了因发生接触椭圆截断而影响轴承可靠性的风险。

未来,针对不同型号与结构的风电机组,笔者拟采用上述在线测试和仿真分析方法,对其进行定制化分析;此外,拟拓展运用仿真分析方法,研究载荷优化对变桨轴承疲劳寿命的影响,从而为载荷优化控制策略的制定提供更为全面准确的依据。