波浪水头对大坝孔压及稳定性影响研究

刘 聪

(甘肃省张掖市临泽县水务局，甘肃 张掖 734200)

0 引言

近年来，随着水电工程建设的快速发展和技术的不断创新，越来越多的水电站建设在山区或河流弯曲处。这些场址通常会遭受到洪水、泥石流等自然灾害的威胁，需要考虑到大坝的稳定性和安全性问题。波浪水头的产生会对大坝孔压和稳定性造成一定的影响。因此，对波浪水头对大坝孔压及稳定性影响的研究具有重要的理论意义。通过对波浪水头对大坝孔压及稳定性影响机理的研究，可以为水电工程的设计和建设提供科学依据和技术支撑，进一步提高水电站的安全性。

目前有许多学者针对水头对大坝造成的影响进行了研究。刘文洁等人[1]以四方井水库粘土心墙坝为例，考虑库水位联合降雨工况下的坝坡渗透稳定性，并基于Monte-Carlo法分析了可靠度规律，结果表明降雨发生在库水位骤降后期最为危险，应加强监测以防止坝坡失稳灾害的发生。达明昌等人[2]基于非饱和渗流原理，考虑不同降雨强度和类型以及不同库水位变化速率，对心墙坝上下游坝坡的稳定性进行有限元模拟，结果表明降雨类型和强度是影响下游坝坡安全系数的主要因素，该研究为心墙坝极端工况下的风险分析和应急管理提供了参考。苏正洋等人[3]通过有限元模拟研究了中小型均质土石坝坝坡在不同类型降雨和库水位变动下的渗流和稳定性，结果表明不同类型降雨对下游坝坡安全系数影响不同，有无降雨及降雨类型的变化对上游坝坡影响较小，库水位的变动对上游坡影响较大，而降雨对下游坡安全系数的影响更大，为该类土石坝的日常风险管理提供依据。闫俊海[4]研究混凝土重力坝和基岩界面的断裂行为及裂纹尖端应力强度因子，以探讨裂缝位置和接触界面与裂缝相互作用对重力坝稳定性的影响，为相关工程提供参考。黄亮[5]利用BIM软件和FLAC3D有限元软件分别计算了某水电站水库边坡在暴雨和水位升降下的稳定性，结果表明在正常水位下边坡稳定，但在蓄水条件下前缘容易出现变形失稳并垮塌。虽然目前在大坝的稳定性上已经有着较多的研究成果，但缺乏针对波浪水头环境的研究。因此，本文基于数值模拟计算，对均质土坝在受到波浪水头作用时其内部孔压的变化情况进行了研究，分析稳定性和最小安全系数，为大坝的设计提供安全评价。

1 计算方法

1.1 计算模型

为研究波浪水头对均质大坝在渗透稳定性上的影响，以水库大坝为原型建立了均质大坝模型。具体的均质大坝计算模型如图1所示。

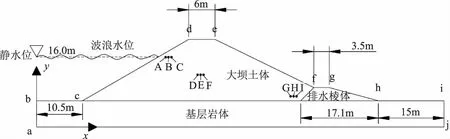
图1 均质土坝数值模拟计算模型

1.2 模型计算参数

在进行数值模拟之前，需要对计算模型在进行数值模拟时所需的材料参数进行确认，包括干密度ρd、有效粘聚力c′、有效内摩擦角φ′、渗透系数kw

以及大坝土体和排水棱体的持水特征曲线。根据该水库的设计图和设计过程采用的工程报告可以得到上述参数和持水特征曲线见表1和如图2所示。

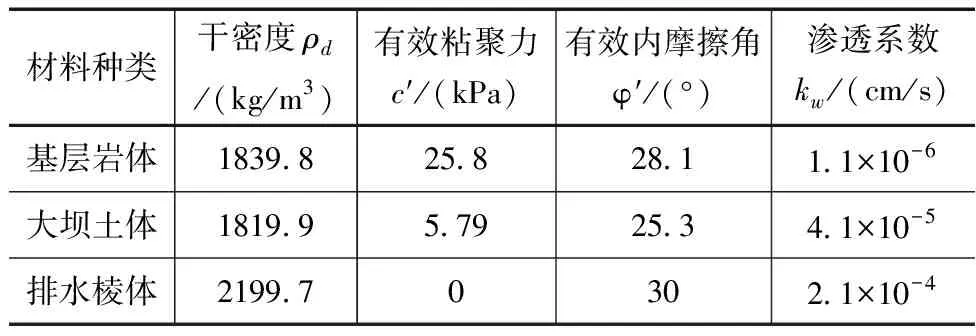
表1 该均质土坝坝体材料工程测量参数

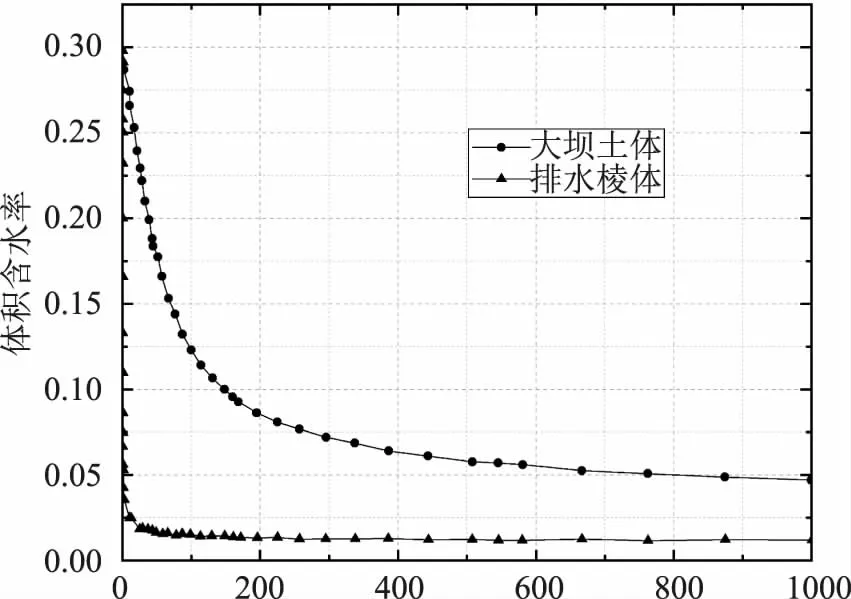
图2 大坝土体以及排水棱体的持水特征曲线

1.3 计算模型边界条件

在进行数值模拟计算时需要先确定计算模型的边界条件，由于本文研究的水头类型为波浪水头，与静水头相比波浪水头会随着时间的变化而发生周期性的变化，因此在进行数值模拟计算时可以将波浪水头采用波形函数表达式的方式去表示，根据已有的研究结果可以得到波浪水头的波形函数表达式如方程(1)所示：

H(t)=H0+(Rp+e)sin(2πt/Tm)

(1)

式中，H(t)—t时刻的波浪水头，m；Rp—波浪爬高，m；e—风壅水面高度，m；t—时间，s；H0—静水头；Tm—平均波周期，s。

根据图1所示的计算模型可以得知静水头的取值为16m，查询规范可得16m静水头所对应的波浪爬高为1.8m，风壅水面高度为0.017m，采用莆田试验站公式可以计算出平均波期为2.97s，因此方程(1)可以写为方程(2)：

H(t)=16+1.817sin(2πt/2.97)

(2)

1.4 模型计算求解方法

如图1所示，模型中被设置了A到I总计9个监测点，分别监测大坝上中下三个不同区域在受到波浪水头作用时内部孔隙压力的变化情况，以计算模型中的a点为坐标原点建立坐标轴后，9个监测点的具体坐标位置见表2。

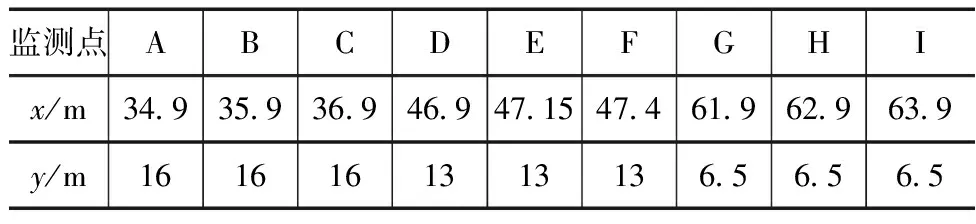
表2 A-I监测点的具体坐标位置

采用数值模拟软件Geostudio对模型进行数值模拟，即可得到大坝在受到波浪水头作用时内部孔隙压力的数值解。

2 孔压变化规律分析

计算模型采用Geostudio进行求解得到的上部区域A处孔压随时间变化曲线如图3所示，上部区域B处孔压随时间变化曲线如图4所示，上部区域C处孔压随时间变化曲线如图5所示。

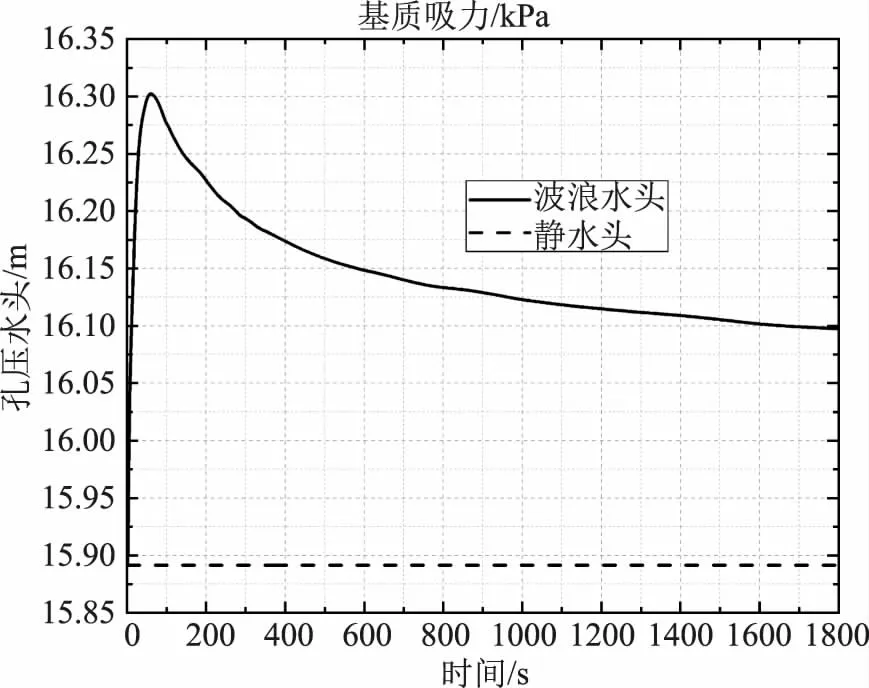
图3 监测点A处孔压变化

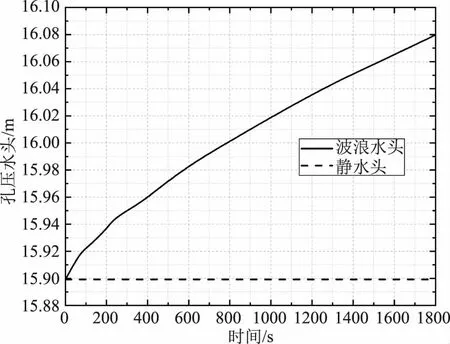
图4 监测点B处孔压变化

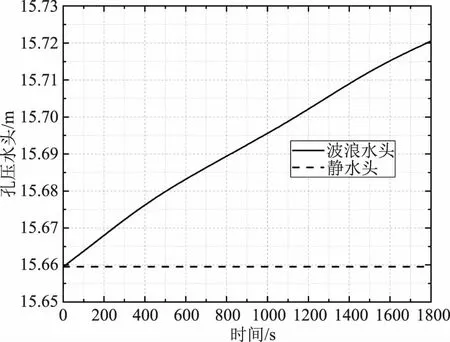
图5 监测点C处孔压变化

从图3—5中可以看出在最靠近水头的监测点A不论是在波浪水头的作用下或是静水头的作用下都有着上部监测点最高的孔压水头。在波浪水头的作用下A点处的孔压水头从15.9m上升到了16.3m，在后续波浪水头的作用下又逐渐降低至16.1m；在静水头的作用下A点处的孔压水头并未发生变化，但无论是在波浪水头的作用下或是在静水头的作用下最大值都在波浪水头的峰值17.8m以下，这种情况的发生是因为在波浪水头进入大坝的过程中并非是以堆积形式进入的，而是在进入的同时发生了孔隙水的渗流，虽然孔隙水的渗流速度小于波浪水头入渗的速度，但任然会发生此类状况。与监测点A相比，监测点B和监测点C处的孔压水头变化逐渐趋于平缓，说明波浪水头对大坝的作用主要集中在坡面处，随着作用距离远离坡面，波浪水头对大坝造成的影响也随之减小。

计算模型中部区域和下部区域的孔压变化曲线如图6—7所示。从图中可以发现中部区域与下部区域的孔压水头几乎不会受到波浪水头的影响，随着波浪水头作用时间的增加，这两个区域的孔压水头几乎保持不变。

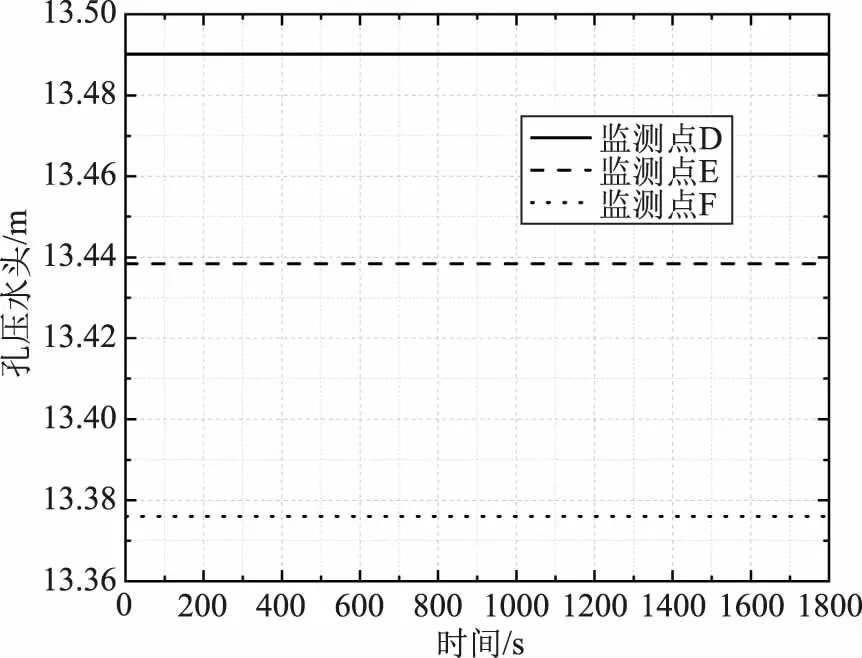
图6 中部监测点孔压水头变化

图7 下部监测点孔压水头变化

3 最小安全系数变化规律

从第2节的分析可以看出波浪水头对中部区域及下部区域几乎都没有造成影响，因此在对安全系数进行研究时仅对上部区域和下部区域进行分析，最小安全系数的计算采用Bishop法，上部区域及下部区域的最小安全系数变化曲线如图8所示。

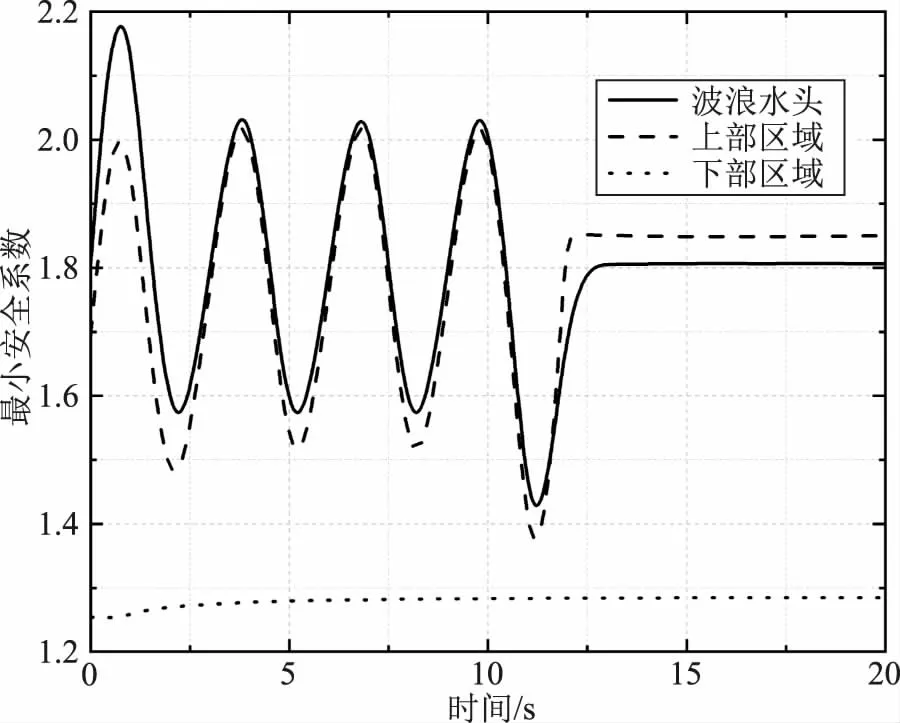
图8 上、下部区域最小安全系数变化曲线

从图8中可以看出本文计算模型在t=0s时的上部区域的最小安全系数为1.7，大于规范要求的最小安全系数1.2，达到了工程设计所需要的抗滑稳定要求；但是当波浪水头开始作用在大坝上时，上部区域的最小安全系数开始呈现出正弦波的变化趋势，其最小安全系数降低至1.02，低于规范要求的最小安全系数，因此上部区域并不满足实际工程应用，存在滑坡发生的风险。

对于下部区域来说，波浪水头的作用并未对下部区域的最小安全系数造成明显的影响，下部区域的最小安全系数仅在波浪水头的作用下从1.24上升至1.29后保持不变，大于规范要求的最小安全系数1.2，表明本文计算模型在受到波浪水头作用时下部区域一直处于安全稳定的状态。

4 结论

本文基于数值模拟法建立了均质大坝模型，采用Geostudio数值模拟软件模拟了波浪水头对均质大坝的影响。结果表明波浪水头对大坝的作用主要集中在坡面处，随着作用距离远离坡面，波浪水头对大坝造成的影响也随之减小。模型在上部区域的初始最小安全系数高于规范所要求的的最小安全系数，在波浪水头作用下安全系数会降低至规范要求之下，存在滑坡发生的风险。模型下部区域的最小安全系数几乎不会受到波浪水头的影响，大坝下部区域的初始安全系数大于规范要求，在波浪水头的作用依然保持良好的稳定性。由于波浪水头对不同大坝类型影响左右存在差异，因此，研究结果应用时需进一步研究。