多维度能量熵提取的不同负载下电机轴承故障诊断
唐 鸣, 王爱元, 朱振田
(上海电机学院 电气学院 上海 201306)
0 引 言
电机轴承对于电机来说是一个至关重要的部件,轴承一旦损坏,就会对电机的运行造成严重的影响。当轴承发生故障时,要迅速诊断出轴承哪个部位发生问题,并及时修复轴承,恢复运行。故障诊断最关键的两个步骤就是故障提取和模式识别。文献[1]采用了改进的时时变换的方法进行降噪然后将特征值提取出来,再对电机的故障类型进行识别。文献[2]先对电机的轴承进行分析,后采用正交小波对故障出现的位置进行诊断。文献[3]在传统模态分解法的基础上,提出了集合经验模态分解法(EEMD),有效避免了模态混叠,但是会造成信号分解的数量出现不同和算法效率低下的问题。文献[4]提出了基于变分模态分解与散布熵(VMD-DE)的坦克行星变速箱故障诊断方法,将变分模态分解(VMD)与散布熵(DE)结合提取其故障特征向量,从而提高故障模式识别的准确率。文献[5]提出了基于VMD的滚动轴承早期故障诊断方法,对采集得到的轴承故障信号用VMD分解提取故障特征输入到包络谱进行分析来判断故障类型。文献[6]提出了一种基于VMD和自回归(AR)模型为基础的转子裂纹故障诊断方法,利用VMD方法得到若干个平稳的本征模态函数并建立各分量的AR模型,把模型参数和残差的方差作为系统状态特征向量。文献[7]提出了小波包能量熵与深度置信网络(DBN)结合的方法对轴承故障进行诊断。先利用小波包分解轴承的故障振动信号,再以能量熵的形式组成特征向量,采用DBN的深度模型对能量熵特征向量进行故障识别。文献[8]采用了一维卷积神经网络的轴承故障诊断方法,在此基础上对超参数进行调节,最终得到了一个较好的模型。本文则采取VMD分解三个维度的故障振动信号并提取能量熵作为特征向量,使得故障的特征更精确地表现出来并输入到CNN模型进行训练并验证[9]。
1 VMD分解与能量熵提取
1.1 VMD分解原理
变分模态分析是一种应用于信号分析中的分析方法。该方法在获得分解成分时,用迭代式搜索变分模型的最优解,来决定各个成分的频率中心和带宽,这样就可以对信号进行频域剖分,并对各个成分进行有效地分离[10-11]。
利用VMD算法将故障信号分成若干个“本征模态函数”,可以表示为
uk(t)=wk(t)cos[φk(t)]
(1)
式中:uk(t)为VMD分解后的第k个的信号分量;wk(t)为信号的瞬时幅值;φk(t)为信号的相位。
信号的瞬时频率ωk(t)的表达式为
ωk(t)=dφk(t)/dt
(2)
通过VMD分解,可以得到k个模态分量uk(t),为了确保原信号和各个模态分量相等,使每个分量估计带宽之和最小,并确定各个分量的中心频率。
VMD算法的具体的步骤如下:
(1) 通过Hilbert变化计算出各个模态分量uk(t)的单边频谱:

(3)
(2) 对每一种模态分量,求出一个大概中心频率ωk,再把单边频谱转化为基频带,其表达式如下:

(4)
(3) 计算出基频带梯度范数的L2,求出大概的各个分量的带宽。

(5)
采用VMD算法分解信号时,将会受到约束,约束的表达式为
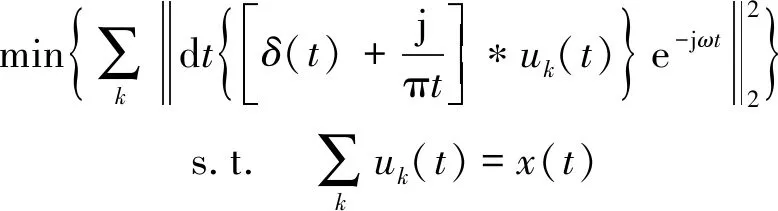
(6)
式中:δ(t)为单位脉冲函数;*是卷积;dt是对函数求导;s.t.是约束条件。
对式(6)引入二次惩罚因子α和拉格朗日乘法算子λ(t)后,其表达式如下:
L({uk},{ωt},λ)=

(7)
使用交替向乘子法(ADMM)算法进行不断地循环迭代,直到搜索到拉格朗日函数L的最小值,停止迭代,并更新uk、ωk、λ直到满足收敛误差ε大于相对误差e。
1.2 能量熵
通过VMD分解电机轴承故障信号,可以得到不同的内禀模态函数(IMF)分量。由于故障信号不同,其中的能量也各不相同。能量分布在所分解的各个分量中,可以作为特征向量来反映故障信号[12-13]。能量熵的表达式为[14]

(8)
式中:pr为第r个IMF分量的能量在总能量Esum中的占比,pr=Er/Esum;Hi表示第i个IMF能量熵,i=(1,2,…,n)。
2 卷积神经网络
卷积神经网络(CNN)由输入层、卷积层、池化层、全连接层以及输出层组成。通过构造合适的网络结构与参数组合,使原始样本数据在卷积层和池化层进行交替迭代,目的是达到对样本数据进行特征提取和学习。在卷积层中,利用卷积与上一层的特征激活图,对其进行卷积运算,再将操作结果代入到激活函数中,得到卷积层的输出。
第i卷积核的输出可表示为

(9)
式中:k是输入特征图的总个数;f(zl)为激活函数;w为卷积核;b为偏置量。
普通卷积的参数量大小计算公式为
C=Z*Z*K*N
(10)
式中:Z为卷积核的大小;K为输入特征图的数量;N为输出特征图的数量。
卷积运算图如图1所示。

图1 卷积运算图
3 故障诊断流程
由于电机轴承结构的复杂性和故障的相关性,使得其故障信号异常复杂,呈现出非平稳性和非线性的特征[15]。然而,以本文所提出的VMD能量熵输入到卷积神经网络故障诊断方法为基础,可以通过VMD分解出有用的 IMF分量。并计算IMF分量的能量熵,组成向量特征,代入训练好的CNN模型中,进行电机故障诊断[16-17]。其流程图如图2所示。

图2 电机故障诊断流程图
4 试验结果与分析
4.1 试验数据
本次轴承故障数据采用上海某电机厂的轴承数据,轴承故障分为内圈磨损、外圈磨损和保持架断裂三种类别。为了更加全面地诊断轴承情况,每种类别再分为负载0%、25%和50%,共9种不同的轴承故障。每个故障类别都提取三个维度的振动信号,即横向、径向和轴向。三个维度的振动信号都进行VMD分解,分解出的IMF分量再进行能量熵的提取组成特征向量,所以每个故障都有15个特征向量,这样提取出的故障信号更加精确,最大程度将故障的特征体现了出来。每种故障取50个故障样本,其中35个为训练样本,另外15个为测试样本。再分别为每种故障贴上标签,例如内圈磨损负载为0%的情况为1,然后根据不同的类别和不同的负载情况依次贴上标签,具体故障数据集如表1所示。
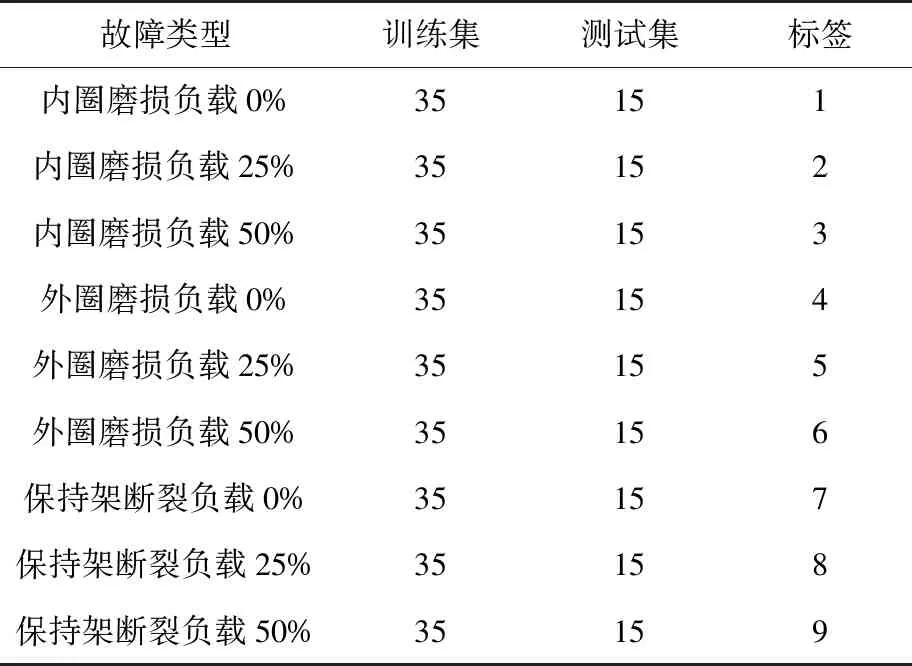
表1 故障数据集
4.2 VMD能量熵
VMD可以对信号中的相似成分进行有效地分离,并且具有良好的鲁棒性,可以有效地解决在信号末端的干扰效果问题。对每组数据样本进行VMD分解,其中分解层数K设置为5,惩罚因子α设置为2 500,其余都设置为默认值。图3~图11分别是各种故障类别的VMD分解图,由于篇幅关系只展示每个故障的横向分解图。
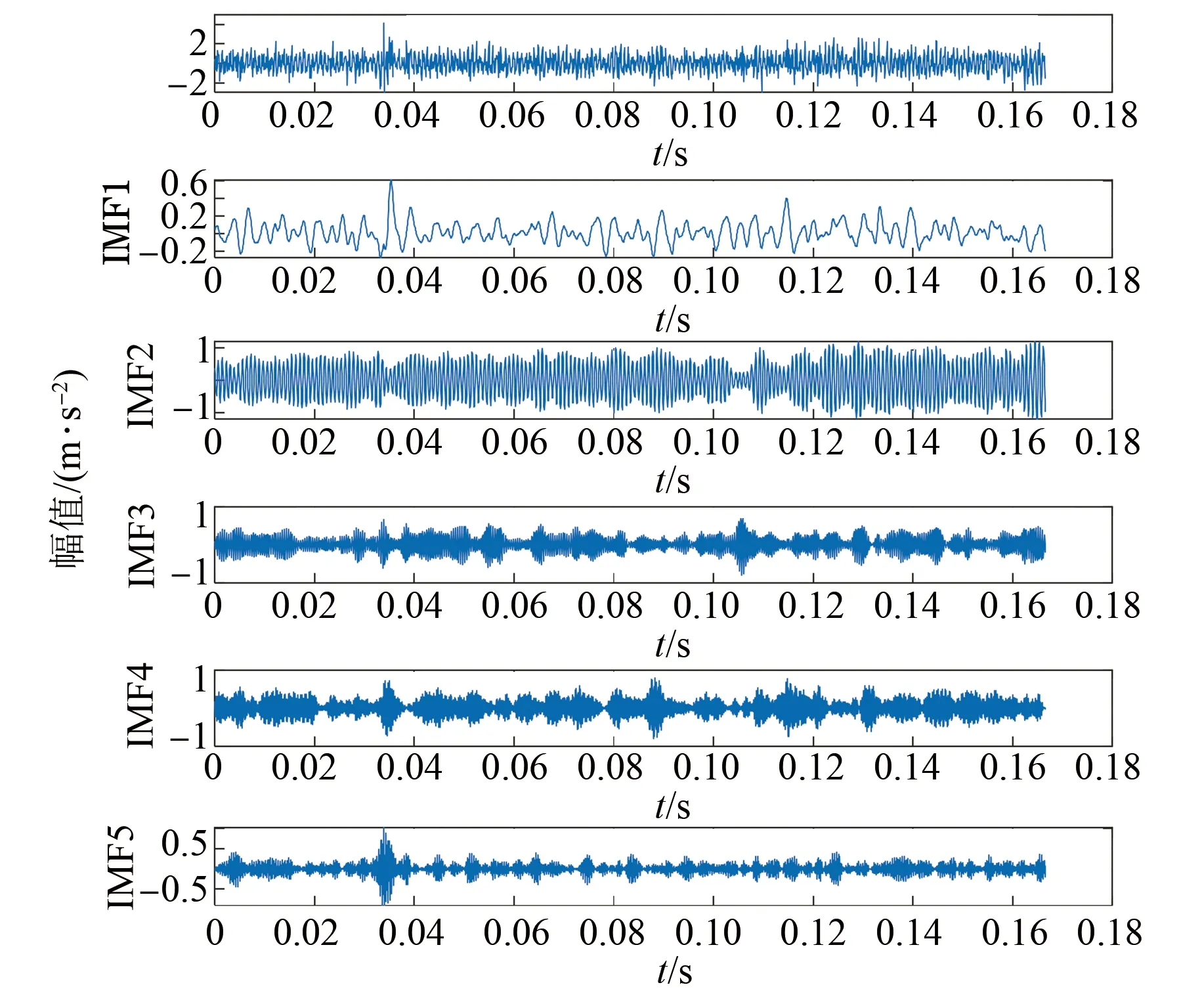
图3 内圈磨损负载为0%的分解图

图4 内圈磨损负载为25%的分解图
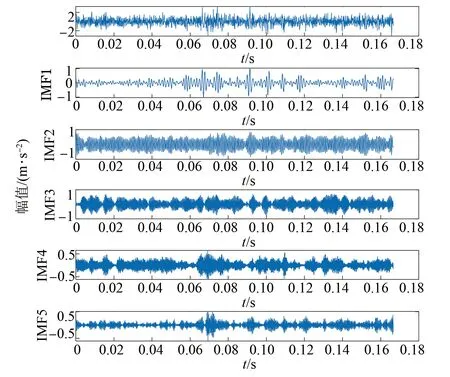
图5 内圈磨损负载为50%的分解图

图6 外圈磨损负载为0%的分解图
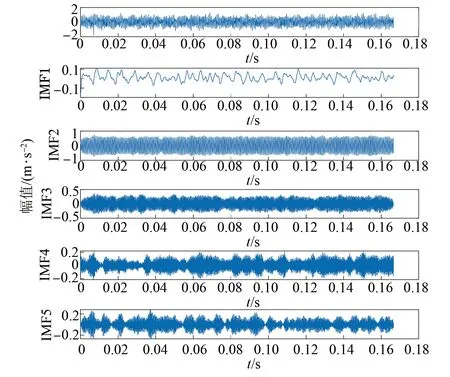
图8 外圈磨损负载为50%的分解图

图9 保持架断裂负载为0%的分解图

图10 保持架断裂负载为25%的分解图
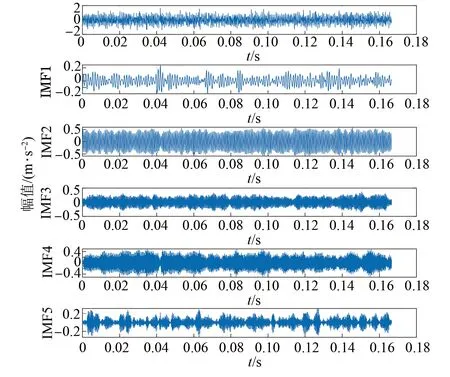
图11 保持架断裂负载为50%的分解图
对比这9个分解图的每种故障横向分解图可知,不同频段的能量不相同,故障的径向和轴向分解图亦是如此。在特征提取上采用VMD分析进行信号处理比直接进行信号处理更加准确。凭借此特性可以区分出轴承故障状态以及故障的类型。经过VMD分解后得到能量熵的故障特征向量,如表2~表4所示。
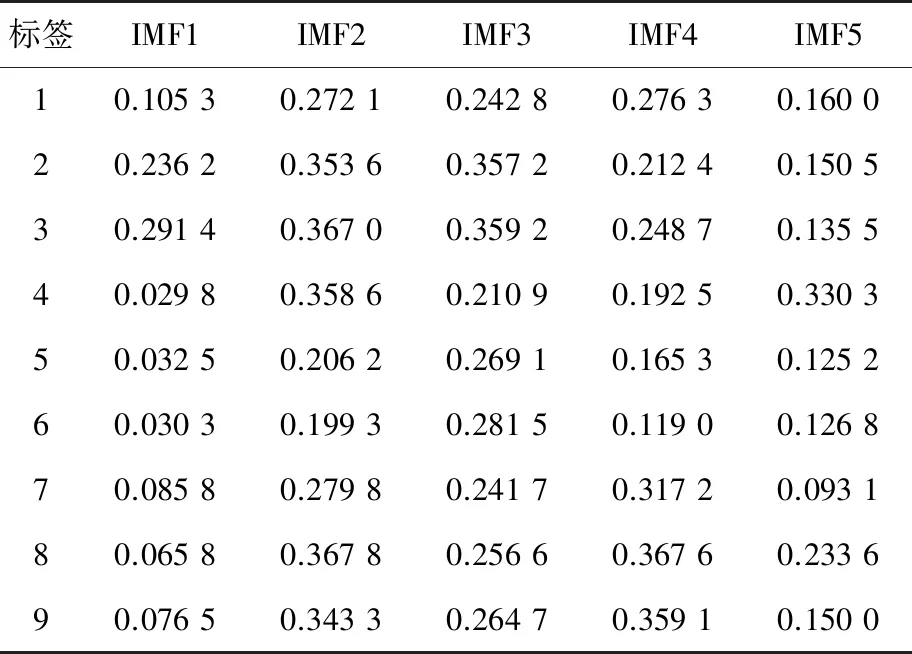
表2 横向各故障的特征向量
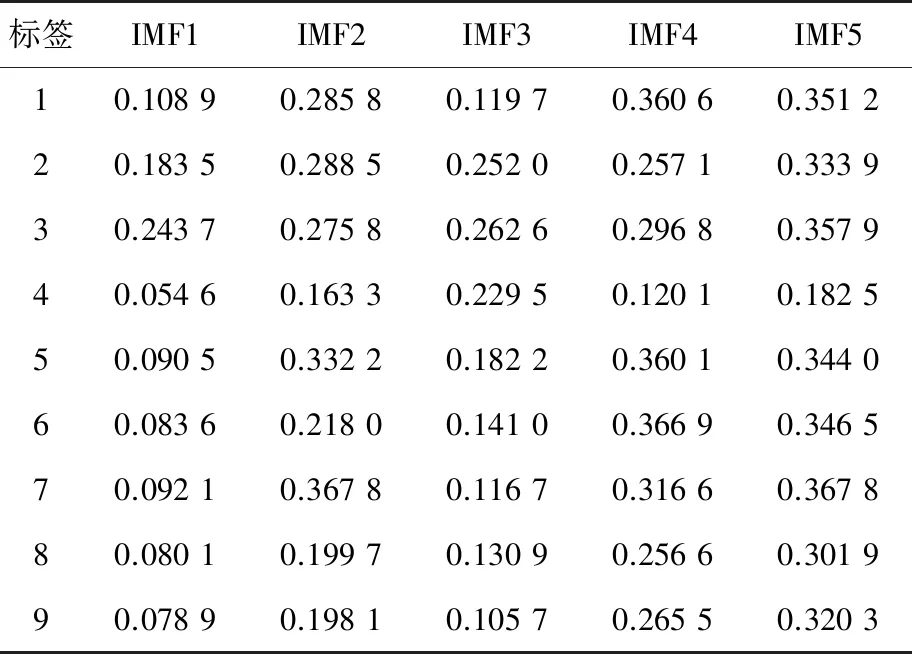
表3 径向各故障的特征向量
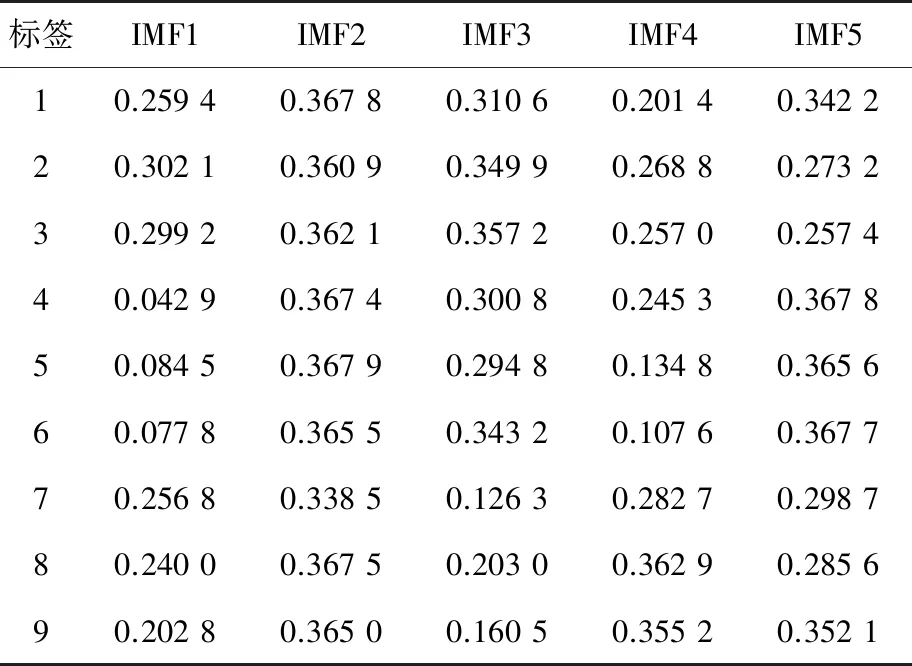
表4 轴向各故障的特征向量
从表2~表4可以看出经过VMD分解过的各个的IMF模态分量的特征向量都不一样,这样一来每一个轴承故障都有15个特征向量。显然用VMD分解后得到的能量熵对轴承故障识别是有效的,可以保留精确的有效信息,尽可能将故障的特征表现出来,从而为输入CNN模型后能够快速、精确地识别出故障类别打下基础。
4.3 故障识别
将不同的故障特征向量输入到CNN模型进行训练,再打乱进行测试。每个故障选取50个样本,共计450个样本进行测试。测试的结果如图12和图13所示。为了体现本文方法的可行性和精确度,采用控制变量法,只改变维度,与只采取横向的、径向的、轴向的能量熵的轴承故障识别作比较,结果如表5所示。

表5 不同维度提取的轴承故障识别正确率对比 %

图12 训练集分类结果

图13 测试集训练分类结果
根据图12和图13可知,训练集的315个样本全部预测正确,测试集的135个样本只有一个预测错误,正确率高达99.259 3%。根据表5可知,单个维度,无论是横向、径向和轴向都没有三维的故障识别正确率高,足以证明本文方法的可行性。
5 结 语
对于电机轴承故障信号难提取,难以全面精确地体现出来,类型难识别等问题,很多文献要么提取定子电流信号,要么只提取一个维度的故障特征。本文则采用了三个维度的VMD分解故障振动信号,提取了各个维度的能量熵并输入CNN模型进行训练相结合的方法来完成诊断。试验结果表明,该方法采取多个维度的能量熵的提取方式可以更加全面、精确地体现故障的特征,使故障诊断的正确率大大提高。

