基于ST-SVD与WOA-SVM模型的变压器绕组松动故障诊断方法*

薛健侗, 马宏忠

(河海大学 能源与电气学院,江苏 南京 211100)

0 引 言

变压器作为电力远距离输送的核心设备,其正常运行是维持电网安全、可靠的关键,因此也是变电站运维的重点对象[1-2]。然而,变压器绕组由于固有的运输安装过程中产生的轻微移位以及长期经受短路冲击电流造成的松动变形情况,使得该原因导致的事故发生率成为首位[3-4]。因此,研究变压器绕组松动故障诊断技术,及时发现、排查出变压器绕组故障隐患,对变压器稳定运行具有重要的现实意义[5-6]。

由于变压器绕组松动与变压器异常振动存在因果关系,因此目前振动法被广泛应用于变压器的故障诊断[7],基于变压器振动信号的时频分析一直是热点。文献[8]采用快速傅里叶变换(FFT)方法对变压器振动信号进行处理,揭示了振动信号50 Hz分量及其部分倍频分量等新特征频率来反映变压器内部绕组松动变形故障,并基于此建立了诊断模型,实现了绕组松动故障诊断与初步定位。文献[9]采用希尔伯特-黄变换(HHT)方法,对变压器振动信号经验模态分解(EMD)后的各层本征模态函数(IMF)进行希尔伯特变换,以三维希尔伯特能量谱及边界谱反映变压器隐含的铁心振动特征。文献[10]基于小波变换方法,对变压器开关切换产生的绕组振荡波进行时频特性分析,通过量化时频信号特征反映变压器绕组的机械状态。上述信号分析方法都在处理变压器振动信号方面取得了良好效果,但此类方法仍有其局限性,例如小波变换的母小波和分解层数的确定会直接影响信号分析效果,HHT对噪声敏感容易导致结果误差较大等。S变换(ST)是近年兴起的一种时频分析方法,其窗函数宽度随信号频率变化而变化,对信号的分辨率高且抗噪能力强,十分适合处理非平稳信号[11]。同时,奇异值分解(SVD)是一种成熟的矩阵特征提取技术,其已和多种时频分析方法结合,应用于图像处理、模式识别等许多领域[12]。

支持向量机(SVM)是一种常用的机器学习方法,在处理小样本集分类时展现出独特的优越性[13]。文献[14]将鲸鱼优化算法(WOA)引入SVM模型中对惩罚因子c与核函数参数g进行寻优,利用随机森林(RF)特征优选构建变压器油中溶解气体特征向量,实现变压器故障诊断模型的构建,验证了WOA-SVM模型的优越性,实现了较好的应用效果。

综上所述,本文提出一种基于ST-SVD与WOA-SVM模型的变压器绕组松动故障诊断方法。首先采用S变换得到变压器振动信号的时频矩阵,经转化为幅值矩阵后进行SVD得到相应的矩阵奇异值,然后定义特征奇异值并提取出来组成特征向量,最后采用WOA优化SVM的c、g参数,输入训练样本构建WOA-SVM模型并对测试样本进行分类诊断,通过与K-means聚类、SVM和粒子群优化(PSO)-SVM模型的诊断准确率进行对比,验证了本文所提方法的有效性与可行性。

1 S变换和SVD

1.1 S变换原理

S变换是Stockwell等[15]于1996年提出的信号处理方法,其综合了小波变换和短时傅里叶变换的特点,其窗函数与频率相关,对噪声不敏感,信号分辨率高,十分适合处理非平稳信号。

对于连续时间信号x(t),S变换如下:

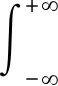
(1)

(2)

式中:w(τ-t,f)为高斯窗函数;t为平移因子;σ=1/f。

由此可以看出,S变换的高斯窗函数的宽度和高度随着频率f的变化而变化,因此在低频段具有高频率分辨率,在高频段具有高时间分辨率[16]。

实际应用中,S变换需离散化处理,可表示为

(3)

1.2 SVD特征提取

矩阵经过SVD得到的奇异值能够充分表示矩阵包含的信息[17],因而广泛应用于信号的特征提取。任意一个矩阵Mm×n,存在着正交矩阵Um×m和Vn×n,将其分解为

M=USVT

(4)

S=diag(σ1,σ2,…,σr,…,0)

(5)

式中:σ1,σ2,…,σr为矩阵M的奇异值。

变压器振动信号经S变换后得到的是时频矩阵,需将各元素求模后得到幅值矩阵再进行SVD。因此,得到奇异值σ1,σ2,…,σr反映的是所采集变压器振动信号的特征量,并且由相应幅值矩阵唯一确定[18]。由于奇异值个数受到幅值矩阵行列数大小的影响,一般数量很多,因此需进一步处理从而突出变压器振动信号在绕组正常与松动状态下的相对变化[19]。本文选择计算所有奇异值的最大值k1、平均值k2和标准差k3作为特征值。表达式如下:

k1=max(σ1,σ2,…,σr)

(6)

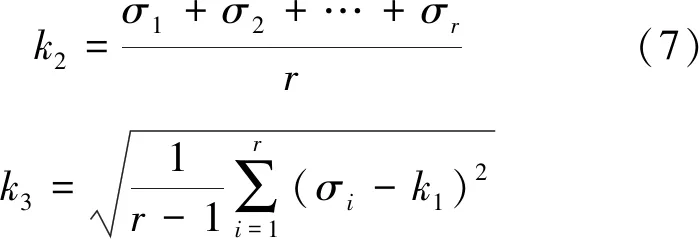
(8)

将三个特征值组成特征向量[k1,k2,k3],通过各元素的变化,反映变压器绕组正常与松动状态下的特征信息,作为本文故障诊断的依据。

2 WOA-SVM模型

2.1 WOA

WOA是Mirjalili等[20]于2016年提出的新型群智能优化算法。该算法模拟了鲸鱼捕猎时选择包围猎物和发出气泡网的两种行为,用来进行参数寻优。算法前期体现出全局搜索,后期体现出局部搜索,其具有参数量少、过程简便的特点。假设解空间维数为D,则鲸鱼个体的位置为

X=(x1,x2,…,xD)

(9)

每只鲸鱼选择包围猎物和发出气泡网的概率相等,都为0.5。

若选择包围猎物,则还分为向最优个体位置移动和向随机个体位置移动两种情况。

向最优个体位置移动时,位置更新公式为

X(t+1)=Xbest(t)-A·D

(10)

D=|C·Xbest(t)-X(t)|

(11)

A=2a·r-a

(12)

C=2·r

(13)

式中:Xbest(t)表示当前最优个体位置;a随迭代过程从2线性减少到0;r为[0,1]的随机向量。

向随机个体位置移动时,位置更新公式为

X(t+1)=Xrand(t)-A·D

(14)

D=|C·Xrand(t)-X(t)|

(15)

式中:Xrand(t)为当前随机个体位置。

两种移动方式的选择条件为:|A|<1时,向最优个体位置移动;|A|≥1时,向随机个体位置移动。

若选择发出气泡网,位置更新公式为

X(t+1)=D′·ebl·cos(2πl)+X(t)

(16)

D′=|Xbest(t)-X(t)|

(17)

式中:b为定义螺旋形状的常数;l为[-1,1]的随机数。

2.2 基于WOA的SVM参数寻优

SVM因在小样本分类中展现出的优良性能而被广泛应用于工程实际中[21]。实际应用中使用的SWM一般为线性不可分SVM,通过引入核函数,将低维样本空间映射到高维,实现样本类型的划分。线性不可分SVM的概念详见文献[22]。本文采用WOA对影响SVM性能的重要参数——惩罚因子c和核函数参数g进行优化,具体步骤如下。

(1) 初始化WOA各参数,如鲸鱼个数N、最大迭代次数等;设置惩罚因子c和核参数g作为鲸鱼位置向量的元素并赋初值;

(2) 将预测错误率作为适应度函数,因此每次迭代后最低的适应度值即为最优个体;

(3) 每个个体选择包围猎物或者发出气泡网的位置移动方式;

(4) 若选择包围猎物,则根据|A|大小按照式(10)或式(14)更新位置并计算各适应值选出最优个体。若选择发出气泡网,则按照式(16)更新位置并计算各适应值选出最优个体;

(5) 重复进行步骤(3)～(4),直到达到最大迭代次数。

3 基于ST-SVD与WOA-SVM的故障诊断模型

本文所提基于ST-SVD与WOA-SVM模型的变压器绕组松动故障诊断方法的诊断流程如图1所示,具体步骤如下。

图1 基于ST-SVD与WOA-SVM模型的变压器绕组松动故障诊断流程图

步骤1:在变压器表面不同位置放置振动传感器采集振动信号;

步骤2:将振动信号进行S变换得到的时频矩阵转换成幅值矩阵,再对其进行SVD得到多个奇异值;

步骤3:按照式(6)～(8)计算出特征向量,并分为训练样本和测试样本;

步骤4:采用WOA优化SVM的参数c、g,以最佳参数输入训练样本构建WOA-SVM故障诊断模型;

步骤5:将测试样本输入训练好的模型中,输出结果即为故障诊断结果。

4 试验结果与分析

为验证本文所提基于ST-SVD与WOA-SVM模型的变压器绕组松动故障诊断方法的有效性,在试验室环境下搭建了变压器模拟故障试验平台开展试验,如图2所示。

图2 变压器模拟故障试验平台

由图2可知,10 kV变压器低压侧由调压器将220 V电压升高至380 V输入,经限流电阻抑制合闸瞬间产生冲击电流;高压侧接入容量均为30 Mvar的电容器与电抗器以模拟变压器负载情况。由于变压器绕组与油箱顶部相连,振动信号在变压器顶部的采集效果更好,因此试验时在变压器顶部布置三个测点,测点布置图如图3所示。振动传感器为IEPE型压电式传感器,型号为1A212E;采集仪型号为DH5922,采样频率设为20 kHz。

图3 变压器测点布置图

故障模拟采用调节变压器内部绕组预紧螺母松紧程度的方式。分别模拟了变压器绕组正常、预紧力下降40%和预紧力下降80%的状态,故障模拟图如图4所示。

图4 故障模拟图

试验过程中对变压器绕组处于3种状态下的振动信号进行多次采集。以测点1为例,当变压器绕组处于预紧力下降40%状态下的振动信号时域图如图5所示。对其进行S变换后对所得时频矩阵求取幅值矩阵,所得时频谱图如图6所示。

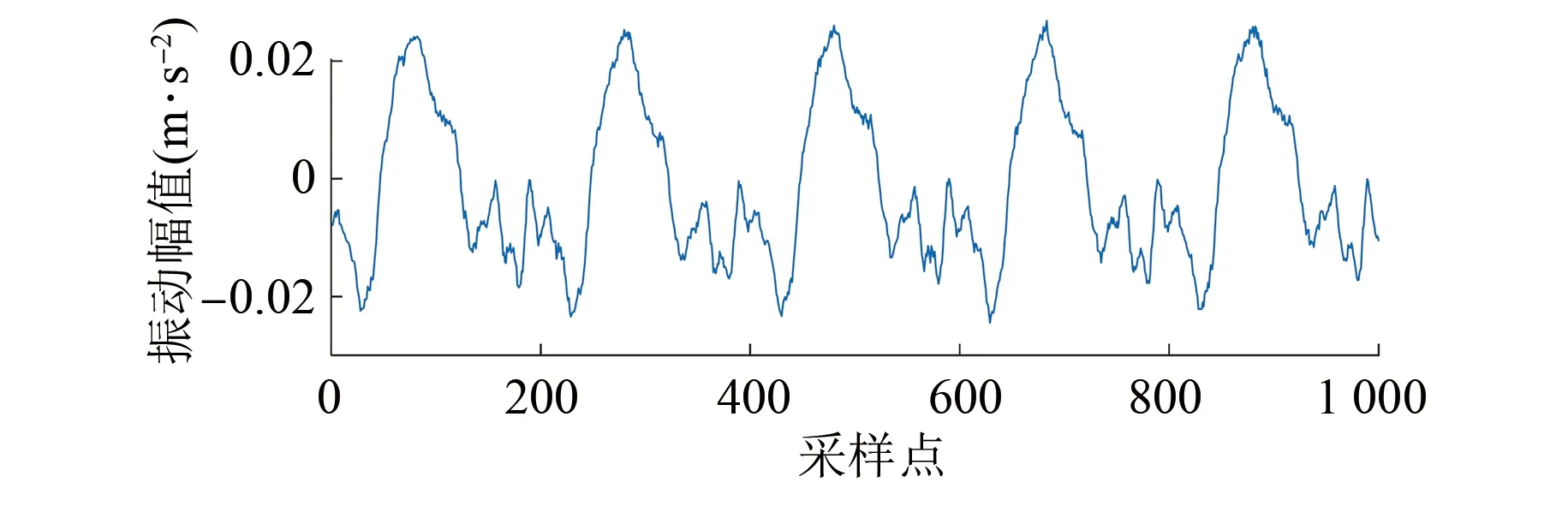
图5 变压器绕组处于预紧力下降40%状态下的测点1振动信号时域图

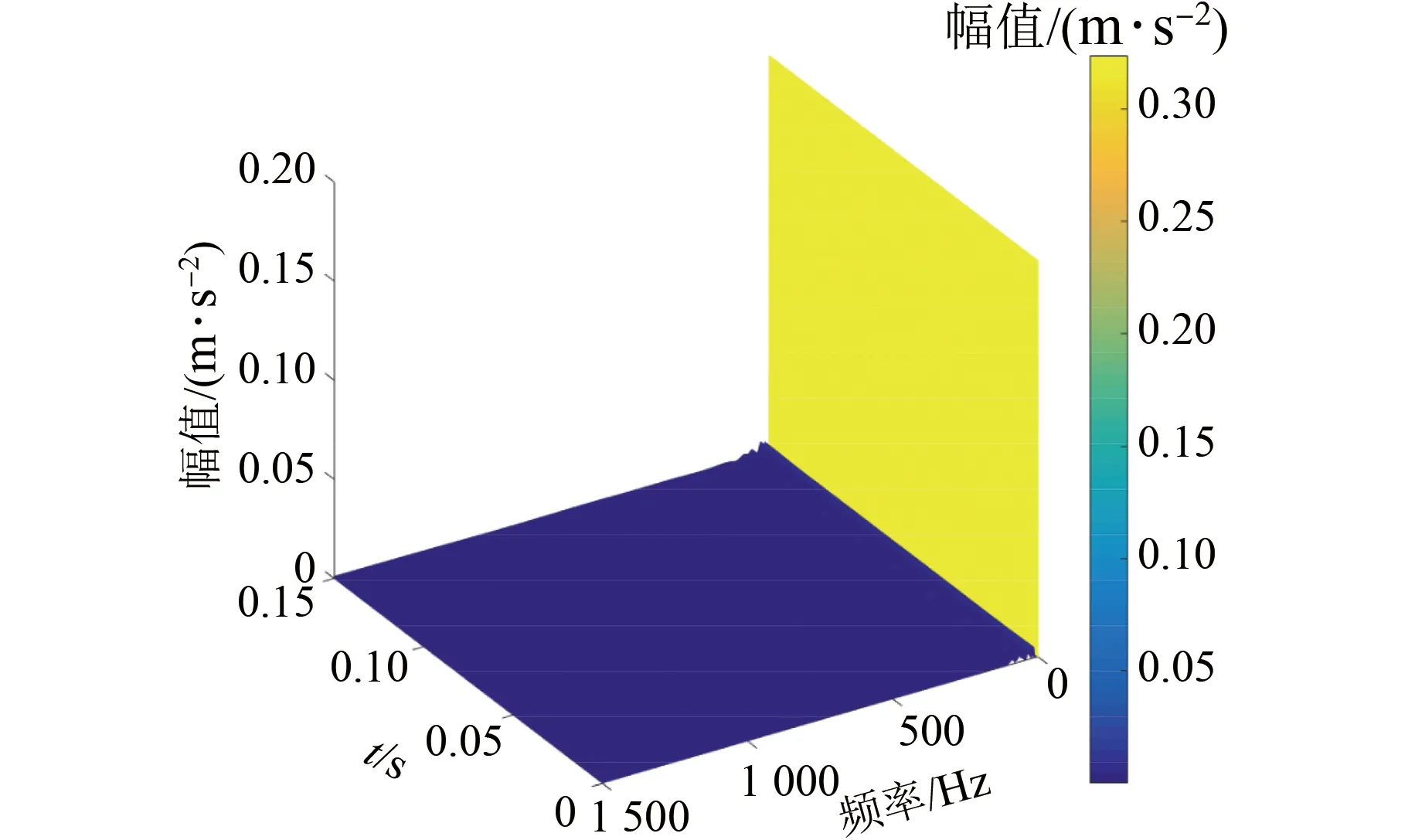
图6 S变换时频谱图

在得到变压器3种状态振动信号的幅值矩阵作为特征矩阵后,对其进行SVD,所得奇异值按照式(6)～式(8)计算出相应的k1、k2、k3。表1为其中的一组计算结果。

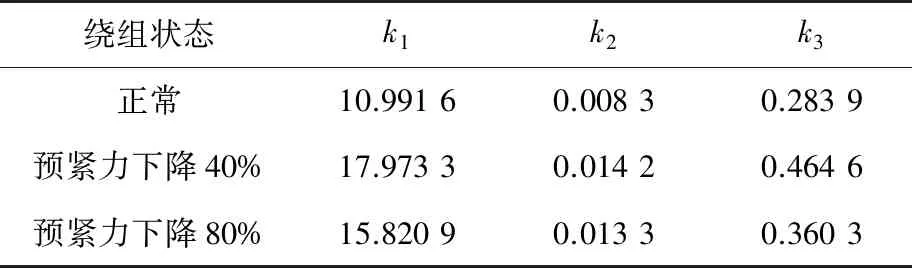
表1 特征奇异值计算结果

由表1可知,本文所提变压器绕组处于3种状态下的振动信号所提取的特征奇异值具有较好的区分性,表明基于ST-SVD的故障特征提取方法的有效性,也表明可通过聚类算法对3种状态下的特征向量进行分类。

本文对每种状态的变压器振动信号分别提取150组特征向量作为训练样本,在采用WOA对SVM参数寻优时,设置c、g的取值范围均为[0,500],最大迭代次数为50。同时,为了对比验证本文所提方法的有效性,又构建了K-means聚类、传统SVM和PSO-SVM模型。对每种状态的变压器振动信号额外提取40组特征向量作为测试样本输入上述模型中。各模型的诊断结果如表2～表5所示。图7为各模型诊断结果的对比图。

表2 WOA-SVM模型诊断结果

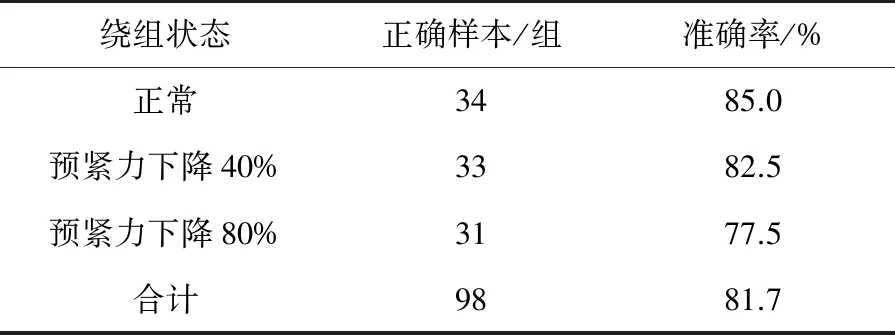
表3 K-means聚类诊断结果

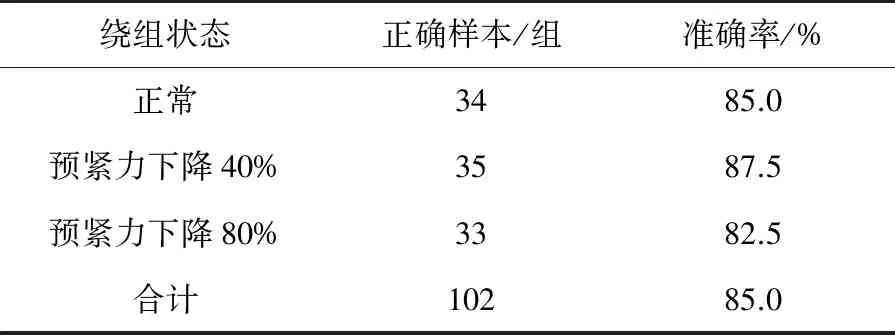
表4 传统SVM模型诊断结果

表5 PSO-SVM模型诊断结果

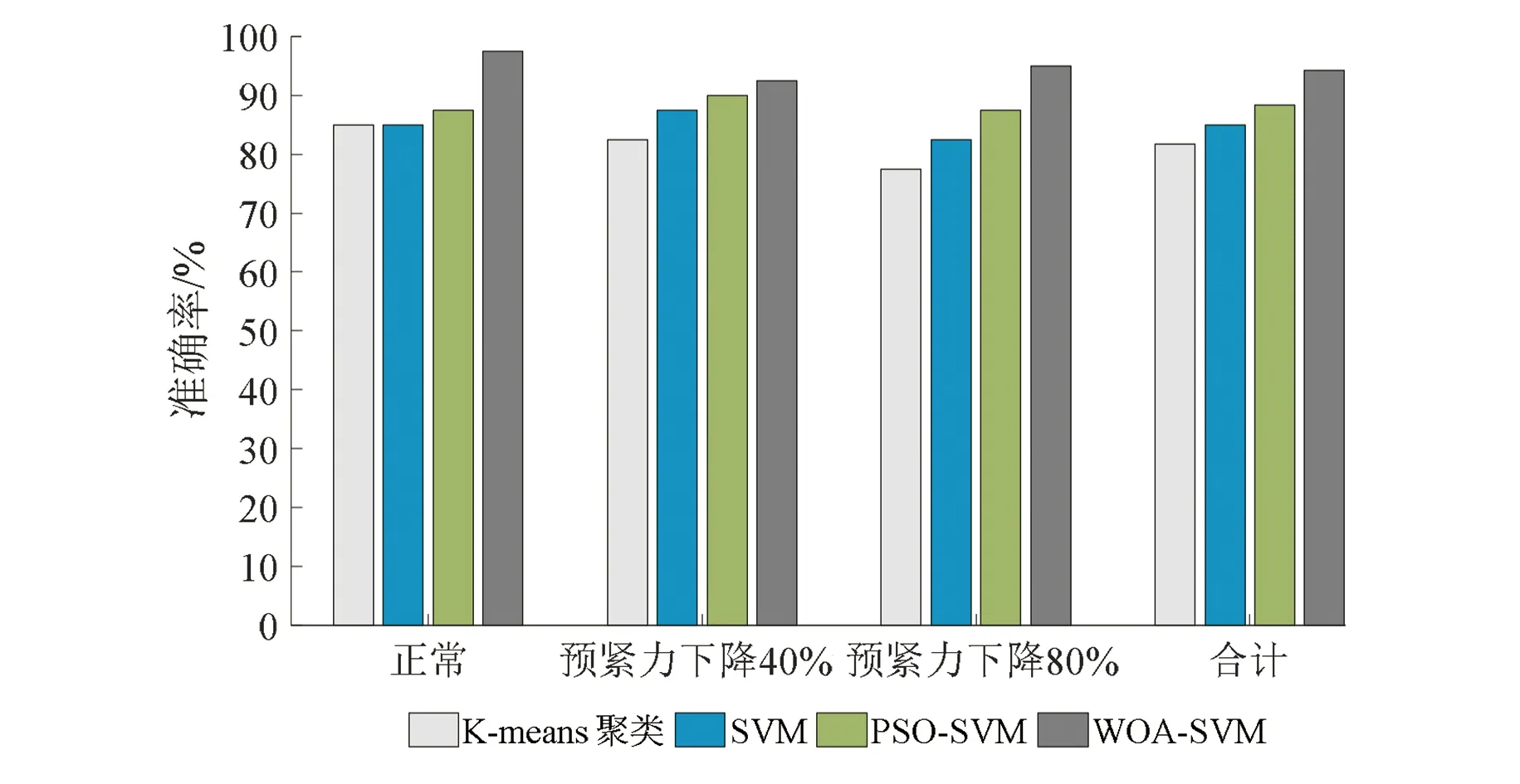
图7 各模型诊断结果对比图

由图7可知,本文所提基于ST-SVD与WOA-SVM模型的变压器绕组松动故障诊断准确率为95.0%,而在输入特征向量相同时,K-means聚类、SVM和PSO-SVM故障诊断模型的准确率分别为81.7%、85.0%和88.3%。这表明了本文所提故障诊断方法的准确率高于传统方法模型,适用于变压器绕组松动故障诊断。

5 结 语

本文提出了一种基于ST-SVD与WOA-SVM模型的变压器绕组松动故障诊断方法。通过S变换获得变压器振动信号的时频矩阵,转化为幅值矩阵后,经SVD得到多个奇异值计算出特征向量,采用WOA优化SVM的c、g参数,用上述特征提取方法提取出的训练样本和测试样本分别构建WOA-SVM模型并验证该模型的有效性,结果表明其诊断精度高于K-means聚类、SVM和PSO-SVM模型的诊断精度。