高重频激光对多激光制导武器干扰机理研究

罗 威,杨华兵,许鹏程,马伟博

(空军预警学院,湖北 武汉 430019)

1 引 言

激光角度欺骗干扰和高重频激光干扰均是对付激光制导武器的有效手段。然而,对于伪随机码等复杂编码激光制导信号[1],以及多目标时产生的混合激光制导信号,激光角度欺骗干扰设备难以做到快速识别告警和有效干扰[2-3]。高重频激光干扰无需对激光制导信号进行解码和复制,可以直接实施干扰。

针对单个激光制导武器目标,研究表明,高重频干扰激光重复频率和激光制导波门宽度对干扰效果影响最大,重复频率越高则干扰概率越大[4-5];激光编码样式、放大电路等对干扰效果也有一定影响[6-7];此外干扰激光需要满足峰值功率、脉宽、波长等基本要求。现代战争中常见发射多枚激光制导武器同时攻击多个目标情况,因此本文针对高重频激光对多激光制导武器目标干扰机理进行了探讨。此外,很多激光器难以同时达到高重复频率和高峰值功率性能要求,用干直射目标代替漫反射方式可降低功率要求[8],但需要高精度跟瞄装置且存在自身安全问题[9],因此需对降低重复频率可行性进行讨论。本文对干扰激光重复频率、干扰反应时间、激光制导波门宽度、信号样式等因素对干扰有效概率的影响进行了研究分析,探讨了提升高重频激光干扰效果的方法。

2 高重频激光干扰机理分析

为对抗转发式激光干扰,半主动激光制导武器中普遍采用激光编码和时间波门技术。激光编码一般是指激光脉冲间隔编码,如精确频率码和有限位随机周期码等;时间波门分为固定波门和实时性波门,波门宽度一般设置为数十微秒量级[2],本文中主要讨论固定波门。

现代战争空对地打击行动中,如攻击机场、桥梁、坦克集群时,一般会发射多枚激光制导导弹同时打击多个目标,即多个激光目标指示器同时照射目标,这时将产生在时域、空域、频域交叠重合的混合激光制导信号。以两个有限位随机周期码激光制导信号形成的混合信号为例,其激光脉冲和时间波门如图1(a)所示。

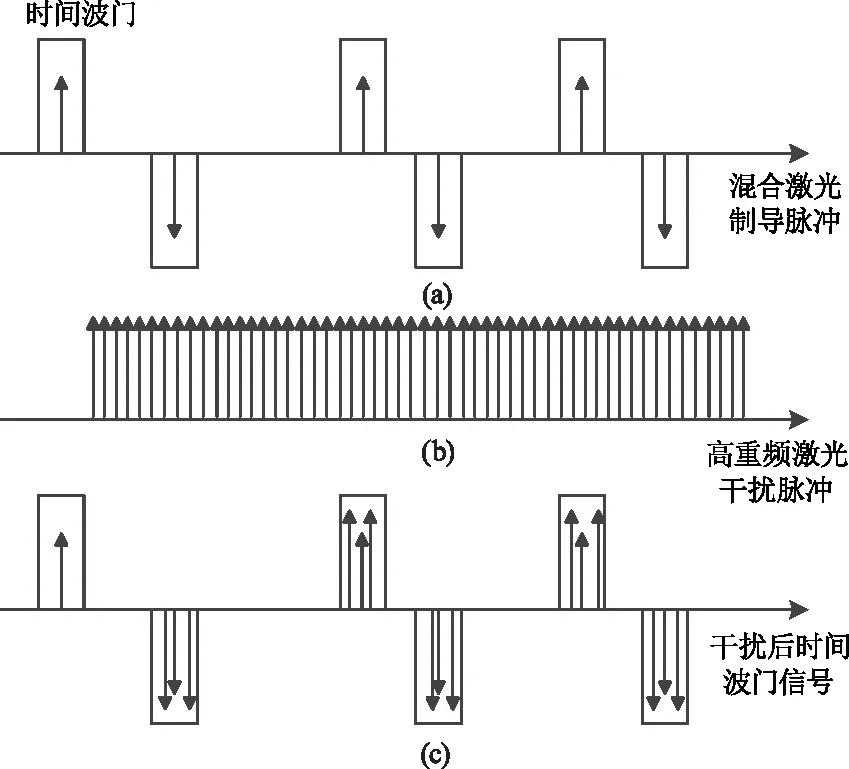
图1 高重频激光对多激光制导武器干扰原理

高重频激光干扰,是指采用高重频激光器作为激光干扰源,直接或者通过假目标反射方式向激光导引头发射重复频率足够高的激光脉冲,如图1(b)所示,使多个干扰激光脉冲进入激光导引头时间波门内,将制导信号淹没在干扰信号中,致使干扰范围内激光制导目标因提取不出信息而迷盲,或提取错误信息而被引偏,如图1(c)所示。

高重频激光干扰效果取决于干扰信号进入波门的个数,且至少有一个干扰信号超前于制导信号,制导信号位于波门中心附近且服从正态分布[5]。因此,本文假设当干扰信号进入波门的个数n≥2时,认为该波门内制导信号被有效干扰。假设整个制导周期内制导脉冲个数为M,被有效干扰的制导信号脉冲个数为m,则高重频激光干扰有效概率为:

(1)

当同时存在多个激光制导目标时,本文认为因当单独计算高重频激光对每个目标的干扰有效概率Pi,总的干扰有效概率Pt则为对每个目标干扰有效概率之乘积。

Pt=∏Pi

(2)

3 高重频激光干扰仿真计算

如前文所述,假设当干扰信号进入波门的个数n≥2时,认为该波门内制导信号被有效干扰。只需统计整个制导过程中被有效干扰制导信号数量与制导信号总数量,就可以计算出有效干扰概率。

因此,本文基于统计算法,利用MATLAB软件编写了高重频激光干扰有效概率计算与分析软件,软件主界面如图2所示。该软件可以设置干扰激光信号重复频率、干扰反应时间和制导激光信号波门宽度、信号编码样式等影响因素参数,可模拟生成混合激光制导信号和高重频干扰信号并进行可视化展示,并计算得到高重频激光对多激光制导目标的单一干扰概率和总干扰概率。

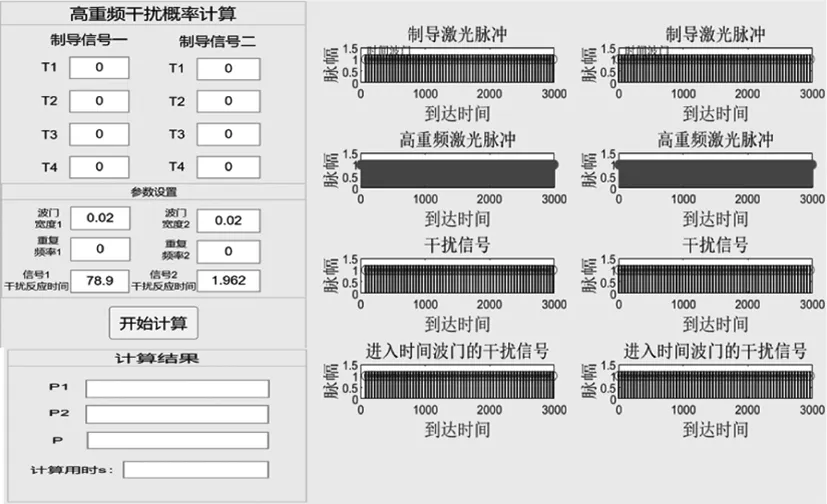
图2 干扰有效概率计算与分析软件主界面

如图2所示,在图2左上角可输入两种激光制导信号编码参数,支持4位以内任意随机周期码及重频编码信号,图左中部分可以设置两种激光制导信号波门宽度、干扰激光重复频率以及干扰反应时间参数。图左下部分分别展示对两种激光制导信号的干扰有效概率以及对2个目标总的干扰有效概率。图右侧部分则对制导激光信号、高重频干扰激光信号、干扰结果等进行可视化展示。

4 高重频干扰有效概率分析

基于上述计算与分析软件,对干扰激光重复频率、激光制导波门宽度、干扰反应时间、制导激光信号样式等因素对干扰有效概率的影响进行了研究分析。

4.1 重复频率与波门宽度对有效概率的影响

考虑两组激光制导信号,均采用有限位随机周期码(简称编码),制导信号一为4位编码,脉冲间隔分别为{45 ms,47 ms,58 ms,61 ms},重复周期ΔT1=211 ms,高重频干扰反应时间t1=8.9001 ms;制导信号二同样为4位编码,脉冲间隔分别为{49 ms,57 ms,67 ms,72 ms},重复周期ΔT2=245 ms,反应时间t2=11.9616 ms。仿真计算三种不同波门宽度B(0.015/0.02/0.025 ms)时,高重频激光干扰对多激光制导目标总干扰有效概率与重复频率的关系如图3所示。

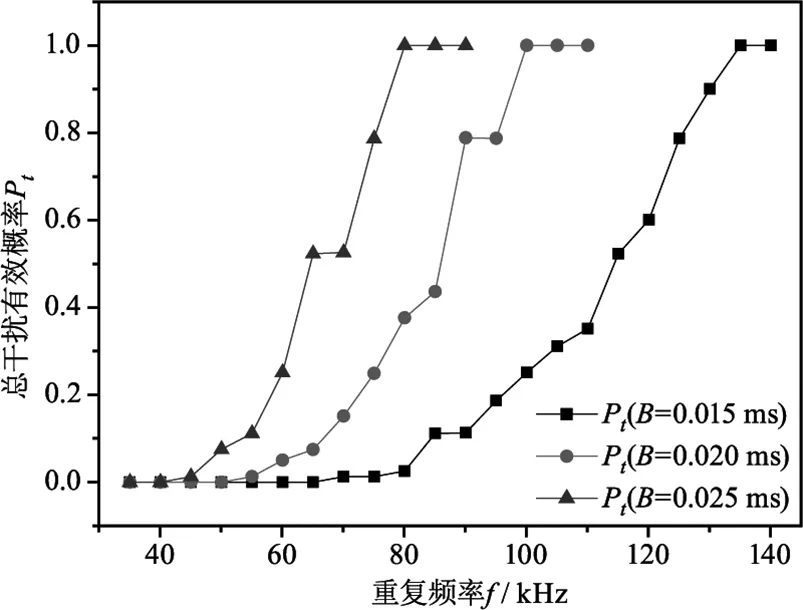
图3 总干扰有效概率与重复频率和波门宽度关系图

由图3可发现,干扰有效概率与重复频率和波门宽度均呈正比关系,即高重频激光干扰的重复频率越高,激光制导导引头波门宽度越宽,干扰有效概率越大。此外,当按照前文所述n≥2时有效干扰的判别标准,重复频率f≤1/B时,最多只有一个干扰脉冲能进入波门,干扰概率下降为0;当重复频率f≥2/B时,最少有两个干扰脉冲能进入波门,干扰概率为100 %。更换参数后多次仿真结果依然满足上述结论。

重复频率与波门宽度是干扰有效概率的主要影响因素,从干扰角度来说,应当尽量提高干扰激光的重复频率;从反干扰角度来说,则应尽量压缩激光制导引导头的波门宽度。

在多目标干扰方面,若采用漫反射假目标方式实施干扰,则单台高重频激光器就可以同时对多个激光制导目标同时实施干扰,干扰过程相互独立,对激光器重复频率和峰值功率也没有额外要求。

4.2 反应时间与信号样式对有效概率的影响

假设高重频激光对制导信号一和信号二的干扰反应时间相同,即t1=t2,其取值在8.91～8.99 ms区间,按照0.01 ms间隔递增。制导信号一和信号二使用与上节相同4位编码样式,形成“编码+编码”组合。作为对照,增加制导信号三和信号四,其采用精确频率码即重频编码,脉冲间隔分别取值53 ms和61 ms,形成“重频+重频”组合。干扰激光重复频率固定为90.1 kHz,计算得到高重频激光干扰对多激光制导目标总干扰有效概率与反应时间和信号样式关系如图4所示。

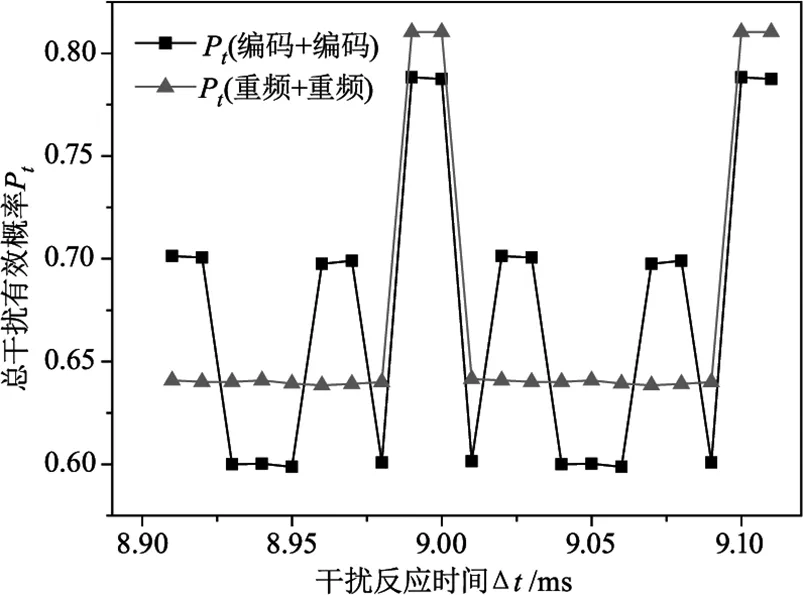
图4 总干扰有效概率与反应时间和信号样式关系图

由图4可发现,随着干扰反应时间的变化,对“编码+编码”和“重频+重频”组合的总干扰有效概率均会产生一定起伏。“编码+编码”组合相比“重频+重频”组合,其抗高重频干扰能力没有明显比较优势。总而言之,干扰反应时间与激光制导信号样式对总干扰有效概率的影响较小,且具有一定的随机性。

另外,分析图4中数据可以发现,总干扰有效概率Pt数值存在一个循环周期,即Δt与Δt+1/f时对应的Pt数值相同。此时,高重频激光脉冲相当于向后移动了一个脉冲,因此在时间波门内出现的位置相同,显然产生的总干扰有效概率也是相同的。

因此,在多目标干扰方面,对于常见“编码”和“重频”激光制导信号,干扰有效概率无明显差别,即高重频激光干扰无需对制导信号进行识别分析,收到激光制导告警信号可立即实施干扰。还可以考虑根据其他告警信息,在接收到激光制导信号之前先释放高重频激光干扰,这样即不会降低总干扰有效概率,还有可能破坏制导武器发射条件和提前对制导过程实施干扰。

4.3 重复频率取整对有效概率的影响

上述两小节仿真计算中,重复频率f均未取整数值(以kHz为单位),如图3中f值分别为(35.1,40.1,45.1,50.1,…130.1,135.1,140.1 kHz),图4中f值则为90.1 kHz。实际上f值取整数和非整数(以kHz为单位)对干扰有效概率会造成较大影响。

只考虑单个制导信号,该信号为4位编码;脉冲间隔分别为{45 ms,47 ms,58 ms,61 ms};重复周期ΔT1=211 ms;时间波门宽度B=0.020 ms;高重频干扰反应时间t1=8.9001 ms。此时,f值取整数(如53,55,57,60,…kHz)和取非整数(如53.1,55.1,57.1,60.1,…kHz)的干扰有效概率如图5所示。

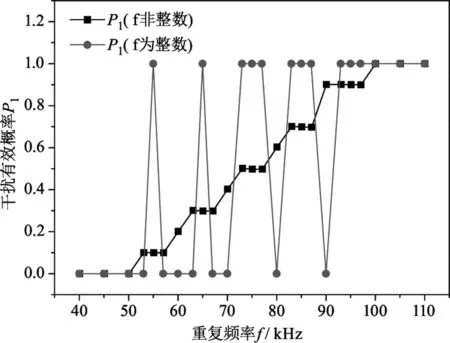
图5 重复频率取整对干扰有效概率的影响

由图5可发现,f值取非整数时,干扰有效概率P1随f值增大而在[0,1]区间近似线性增大,与图3结论基本一致。但当f值取整数时,干扰有效概率P1则只会出现(0,1)两个数值,且随着f值增大,0值出现概率减小,1值出现概率增大。分析其原因如下:令f=MkHz,则高重频激光脉冲的时间周期为1/Mms;激光制导信号重复周期ΔT1=Nms,假设N为正整数。高重频激光和制导激光混合后将形成一个新的周期信号,混合后信号重复周期为1/M和N的最小公倍数,此时高重频激光脉冲在时间波门内位置会重复出现,即能够进入的脉冲数则是相同的。若M为正整数,则混合信号重复周期为Nms,与制导信号相同,即能够进入每一个时间波门的脉冲数均相同,n≥2时P1=1,n≤1时则P1=0。若M为非整数,如取63.11 kHz,即6311个高重频激光脉冲的时间周期为100 ms,高重频激光脉冲在时间波门内位置重复出现的重复周期则为100与N的最小公倍数,该重复周期为较大值(数秒或数十秒),而重复周期之内干扰脉冲在时间波门内位置则具有较强随机性,干扰有效概率更符合统计规律。

对于多目标干扰而言,任意单个目标未受干扰命中目标则防护任务失败。因此,高重频激光实施多目标干扰时必须减少不确定性,即重复频率值应当尽量避免取整数值,并可以增加小数点位数。

5 结 论

高重频激光干扰多个激光制导目标时,与干扰单个激光制导目标类似,重复频率与波门宽度仍然是影响总干扰有效概率的主要因素,而干扰反应时间与激光制导信号样式对总干扰有效概率的影响较小,此外还发现重复频率取整数则会增大干扰有效概率的不确定性。基于上述结论及高重频激光干扰多激光制导目标实际需求,本文针对性提出了 “一对多”、提前干扰、重复频率避免取整数等改进措施,研究结论可为提升高重频激光对多激光制导目标干扰效果提供参考。