抗滑桩不同参数取值对边坡稳定性的影响研究

王济沧 黄康娜 桑庆云

（1济南城市建设集团有限公司，山东 济南 250000；2济南城建集团有限公司，山东 济南 250000）

0 引言

在边坡治理工程中，常常选取经济性好、支护效果好、施工速度快、抗滑能力强的支护措施，而抗滑桩具有以上优点，因此在实际施工中得到了广泛应用。但是每个边坡工程的地质条件不同，抗滑桩的参数选取也不相同。目前普遍采用极限平衡法进行参数选取分析，而极限平衡法也有弊端。极限平衡法虽然假设了桩在支护情况下的受力及滑动变形情况，但并没有体现桩与土之间的相互作用和边坡变形规律[1-2]。利用基于有限元法或者有限差分法的数值分析，可以为研究桩身参数对边坡稳定性的影响提供有效的研究手段[3]。

杨光华等[4]采用FLAC3D软件模拟抗滑桩不同加固位置及尺寸，进而分析边坡的安全性；Won 等[5]采用极限平衡法和FLAC3D相结合的方式，对边坡的稳定性系数以及桩体的力学性能参数进行了研究，并且探讨了边坡的稳定性；王聪聪等[6]对抗滑桩支护加固边坡的效果进行了研究，分析了抗滑桩的最优工况；刘怡林[7]等利用数值模拟软件FLAC3D对不同工况进行了模拟，提出了抗滑桩支护参数的优化方案；戴自航等[8]结合工程实际情况，研究了在施工中抗滑桩的最佳设计方案。在抗滑桩作为支护方式的研究中，主要是针对抗滑桩的各个参数进行优化，其次是探讨边坡的安全系数，但很少考虑桩与土的相互作用机理，也无法体现抗滑桩的内力变化规律以及桩的变形变位规律。由此可知，目前的研究缺少对抗滑桩综合参数的研究，往往根据施工经验确定桩的弹性模量、桩身长度、布桩位置等参数，这样的取值通常比较保守，也缺乏科学性，存在浪费资源的情况。

基于此，本文采用FLAC3D软件进行数值模拟，分别研究抗滑桩弹性模量、加固位置及桩身长度三个参数的变化对边坡稳定性的影响。

1 理论计算模型分析

在FLAC3D软件中采用桩单元进行抗滑桩的模拟，可以获得准确的计算数据。抗滑桩理论计算模型如图1所示。桩-土之间的相互作用通过模拟法线方向和切线方向的耦合弹簧数值计算，耦合弹簧属于滑块与非线性弹簧的组合体，能够实现实体单元与模拟桩单元网格之间的弯矩与力的相互传递。

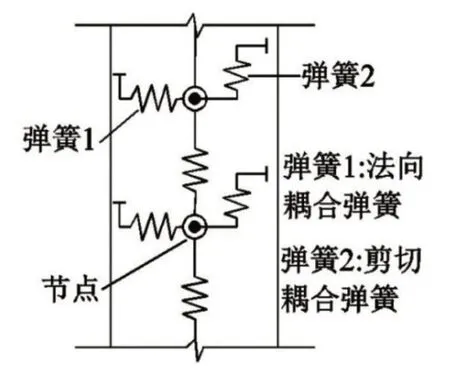
图1 抗滑桩力学计算模型

计算过程中，围岩网格和桩单元节点之间产生相对位移从而产生剪力的计算公式如下：

式中：FS——剪切方向上非线性弹簧产生的剪切力；

L——模拟单元有效单元的长度；

css——剪切连接弹簧的剪切刚度；

usi——抗滑桩的轴向位移；

usm——岩土滑动面的轴向位移。

抗滑桩法线方向非线性弹簧的法向力计算式如下：

式中：Fn——法线方向非线性耦合弹簧产生的法向力；

L——模拟单元有效单元长度；

cns——法线方向非线性耦合弹簧的法向刚度；

uni——垂直于抗滑桩轴向的桩的位移；

unm——垂直于桩轴线方向介质面的位移。

2 数值计算模型建立与参数选取

按平面应变建立边坡计算模型，岩土体变形采用Mohr-Coulomb准则，利用强度折减法计算边坡稳定性系数，将是否收敛作为边坡失稳的判据。利用自编的FISH语言提取滑动面数据，将滑动面上各点的位移量化。

建模分析计算图如图2 所示，露天边坡的倾斜角度较大，夹角假设为60°，属于高陡边坡。根据实际工程的监测数据显示，花岗质碎裂岩与黄铁绢英岩化花岗岩相交的平面易产生相对滑移，从而作为重点研究对象。抗滑桩的设计桩径为2000mm，计算过程中采用的桩长分别为12m、16m、20m、24m、28m、32m 和36m。图2 所示的LX表示为抗滑桩加固位置到坡脚的距离，取值为（6,48），其中，x表示步距，大小为6m；L表示边坡的水平投影距离长度，为48m。岩土参数和桩身参数取值如表1所示。

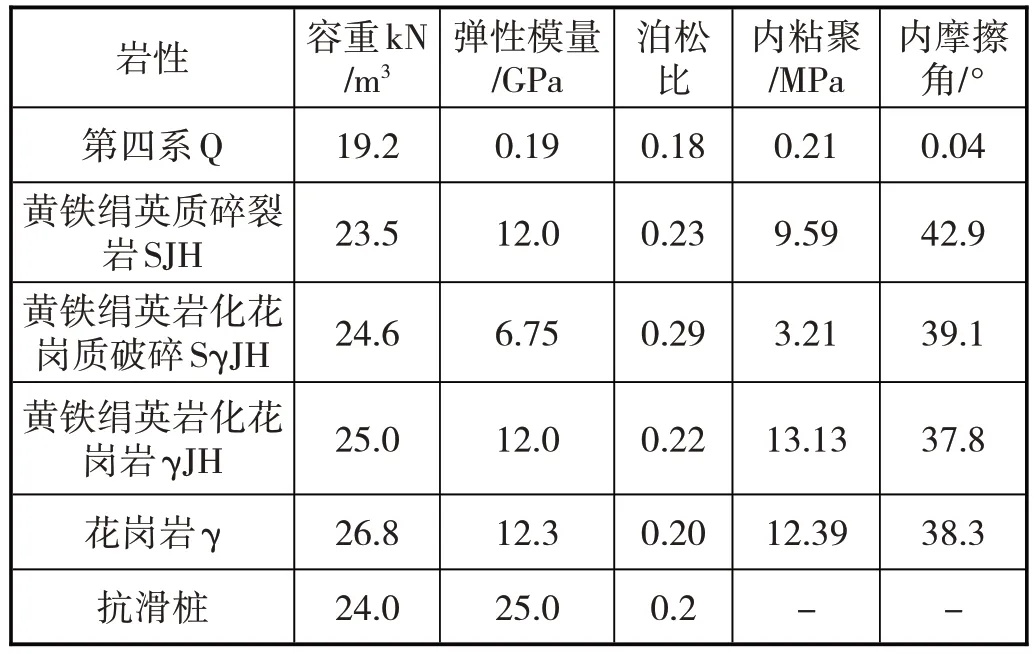
表1 岩土参数与桩身参数

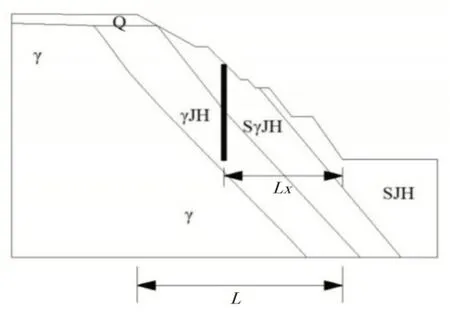
图2 数值计算模型示意图

3 抗滑桩不同参数取值对边坡稳定性影响分析

3.1 抗滑桩不同加固位置的影响

抗滑桩加固边坡时，加固位置对边坡稳定性也有影响。如图3 所示，当抗滑桩的桩长取值较小时，抗滑桩选取的加固位置对边坡的稳定性影响不大。假设抗滑桩的选取位置在坡脚及其附近时，抗滑桩的加固效果并不明显。当设桩位置到坡脚的水平距离与边坡的水平投影距离比值增大时，抗滑桩对边坡的加固效果越明显，边坡的稳定性系数越好。桩长不同，其最优加固位置也不尽相同。当桩长为28m 时，稳定性系数趋于稳定。当桩长为30m 时，最优的加固位置不是在边坡中部，而在位置5，此时抗滑桩加固边坡的效果最好。

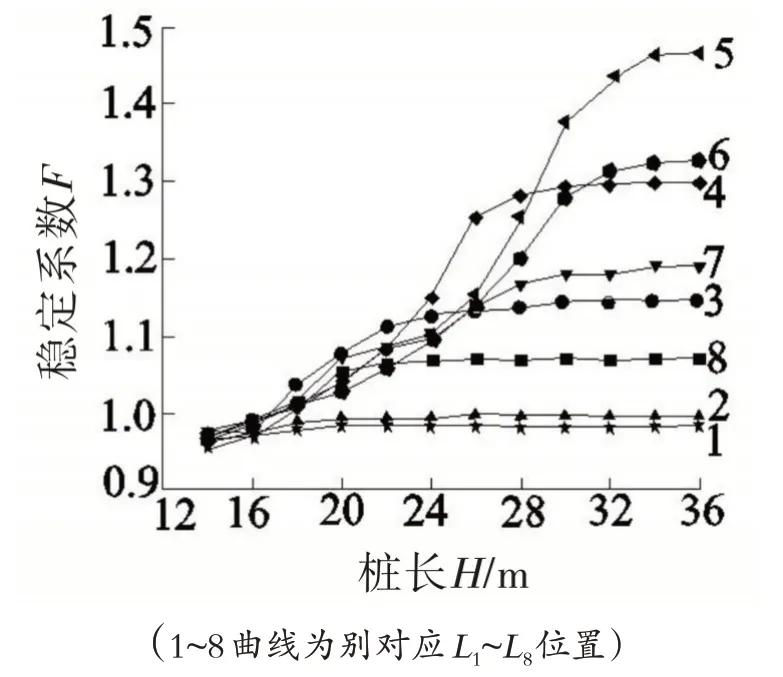
图3 抗滑桩不同加固位置）和桩身长度与边坡稳定系数的关系

3.2 抗滑桩不同桩身长度的影响

由图3 可知，曲线1 和曲线2 为平缓曲线，说明此时桩长对边坡的稳定系数影响不大。在这两个位置，边坡的稳定性系数稳定在1.0 附近，此时边坡不稳定。在位置L3、L7、L8，随着桩长的增加，稳定性系数也随之增大，在位置L7较为明显。此时抗滑桩的桩长越大，边坡稳定性系数也越大，边坡越稳定。在位置L5、L6、L4时，上述现象愈发明显，但无论在哪个位置，桩长大于28m 时，边坡稳定性系数均趋于稳定，此时增加桩长对边坡的稳定性影响较小，反而增加成本，浪费资源。边坡稳定系数随着桩长的增加只是略有增加，甚至趋于稳定。也就是说此时桩长增加，抗滑桩稳定系数不再有明显变化，此时增加桩长不再明显影响边坡的稳定性。推断抗滑桩的有效嵌固深度就在边坡稳定系数反弯点处，根据模拟结果可知，此时抗滑桩的桩长为最经济桩长，即在L5位置有最大的嵌固深度。

3.3 抗滑桩不同弹性模量的影响

在位置L5，最优桩长值为32m，此时边坡稳定性系数接近极值，增加桩长对加固效果并不明显，优化桩的弹性模量继续进行边坡稳定性分析，所得结果如图4所示。

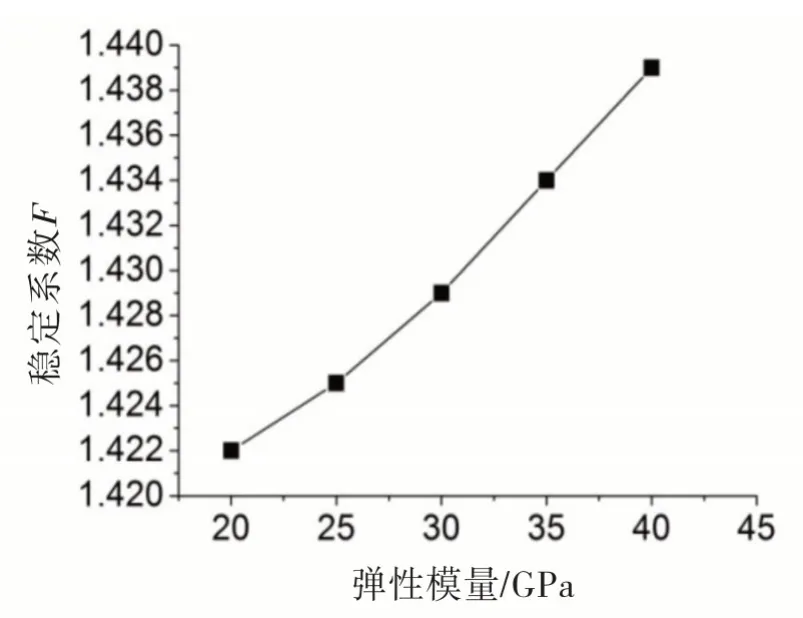
图4 抗滑桩不同弹性模量与边坡稳定系数的关系图

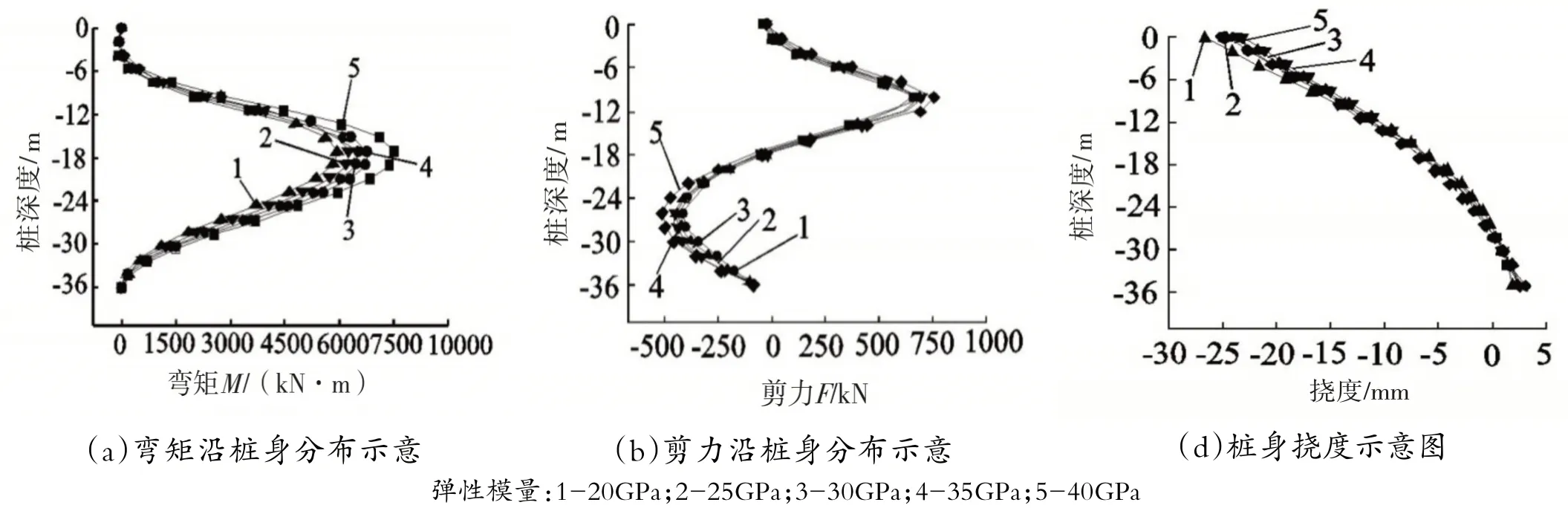
图6 不同弹性模量抗滑桩变矩、剪力、挠度分布示意图

由图4 可知，增大弹性模量并不能使稳定性系数有明显增加，调整弹性模量，稳定系数变化仅为1.15%。且弹性模量在20~40GPa 之间取值时，稳定性系数可以视为不变，因此在此区间取值，弹性模量对边坡的稳定性没有影响。

3.4 抗滑桩不同弹性模量对桩身内力和变位的影响

将抗滑桩的弹性模量作为自变量，其余参数保持不变进行模拟研究，得到采用不同弹性模量的情况下，抗滑桩不同长度处的弯矩、剪力变化规律以及不同桩长的挠度变化规律，模拟结果如图5所示。

由图5 可以看出，桩身弹性模量不断增大，抗滑桩的桩身弯矩及剪力也随之增大。埋深36m 的桩，在埋深约为-18m 时的弯矩最大。充分对比分析模拟结果得出，桩身内力的变化并不显著，弯矩的相对误差仅占18.6%，桩顶挠度的误差仅有3.5mm，并且随着桩深度的不断增大，不同弹性模型工况下其桩挠度也基本一致，曲线基本重合，说明弹性模量的影响不大。

综合对三个主要特征指数（抗滑桩变位、边坡稳定性系数、抗滑桩桩身内力）进行分析后发现：虽然桩身变位随着抗滑桩弹性模量增大而减小，但效果并不明显，在施工过程中收效甚微，在实际施工过程中，一般采用更高强度的混凝土和受力钢筋来提高弹性模量，这会大大提高抗滑桩的施工成本及工期，造成资源浪费。因此，在工程设计阶段，只需根据工程实际合理确定抗滑桩弹性模量，综合考虑工程成本、施工进度及支护效果，一般不采用通过增加抗滑桩弹性模量来提高边坡稳定性系数的方法。

4 结束语

综上所述，本文采用数值模拟的方法，研究了抗滑桩在选取不同参数时的边坡稳定情况，得到如下结论：抗滑桩布置在越靠近坡脚的位置，边坡稳定性越差，且桩长的增加或减小对边坡稳定性影响不大；抗滑桩桩长小于24m 时，抗滑桩桩位对边坡稳定性影响同样不大，当桩长大于24m时，合理布设抗滑桩的位置对提高边坡稳定性有显著的效果；单纯提高抗滑桩的弹性模量并不能有效增大边坡稳定系数，但抗滑桩的位移有一定减小；在实际工程中利用抗滑桩加固边坡时，根据工程实际合理确定抗滑桩的最优弹性模量即可。