资源受限下单批耦合混合流水车间调度问题研究
唐红涛,刘子豪,官思佳
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.武汉理工大学 湖北省数字制造重点实验室,湖北 武汉 430070;3.航天科工空间工程发展有限公司,北京 100854)
混合流水车间调度问题 (hybrid flow shop scheduling problem,HFSP) 是车间调度领域中基础且重要的问题[1],广泛存在于铸造[2]、汽车[3]等领域。混合流水车间中包含多道工序且至少一个工序中包含一台或多台并行机器,同时不同加工阶段之间有严格的加工顺序约束[4]。在生产制造企业中,生产制造过程会发生机器阻塞[5]、资源受限[6]等动态事件,实际生产调度过程中不仅要考虑工序排序和机器选择的问题,还要考虑加工设备附属资源的分配等约束问题[7],因此研究多约束下的混合流水车间调度问题具有很重要的现实意义,资源受限的混合流水车间调度问题 (resource constrained hybrid flow shop scheduling problem,RCHFSP) 正是为解决这一问题而被提出的。
目前,多约束车间调度问题研究获得了较大进展。Costa等[8]提出一种离散回溯搜索算法求解劳动力有限的混合流水车间调度问题。唐红涛等[9]提出一种帝国竞争算法求解砂型铸造车间中噪音和能耗约束问题。但是这些研究主要集中在机器柔性和加工约束上,没有考虑机器附属资源的约束问题,如实际生产中机加工的刀具、铸造生产中合箱使用的翻斗机、熔炼浇筑时需要的除尘机等资源都有数量上的约束。崔航浩等[10]建立有机器准备时间和附属资源约束的多资源受限的车间调度模型,并提出一种多种群粒子群算法解决该问题。Tao等[11]针对最小化完工时间和能源消耗的RCHFSP提出一种改进的帝国竞争算法进行求解。但是这些研究忽略了实际生产过程中存在批处理工序的生产情况,没有对包含批处理的资源受限流水车间调度进行研究。Zhou等[12]设计一种自适应差分进化算法来求解批调度问题。Li等[13]研究工作恶化的并行批处理分布式流水车间问题。这些研究讨论了带批处理的混合流水车间调度问题,但没有考虑附属资源约束的情况。资源受限下单批耦合混合流水车间是混合流水车间的扩展,单批耦合、附属资源约束增加了调度问题的求解难度。
因此,本文首次建立以最大完工时间和总能耗为目标的资源受限下单批耦合混合流水车间调度模型,并提出一种改进的离散蛙跳算法 (improved shuffled frog leaping algorithm,ISFLA) 对模型进行求解,设计一种针对资源约束解码方式,改进了一种适用于单批耦合的NEH初始化策略提高算法性能,并设计了一种改进的模因组搜索策略提高算法的搜索能力,最后通过实验验证了算法的有效性。
1 问题描述和数学模型
1.1 问题描述
资源受限的单批耦合混合流水车间在混合流水车间的基础上增加了批处理阶段与附属资源约束。包括工序排序、机器选择、工件分批和资源分配4个子问题。问题描述为n个工件需要按相同的工艺进行s个加工阶段,每个阶段至少有两台并行机,其中一个阶段为批处理阶段。前一阶段加工完成才能进行下一阶段的加工。工件可以在后续阶段机器集合中的任意一台机器上加工,且加工开始后不能中断。工厂有r种资源,包括{R1,R2,…,Rr}。每种类型的资源数目预先给出,每道工序开始加工前必须保证机器可用且资源数目足够。模型建立之前作出如下假设。
1) 机器在在首个工件到达后启动,不加工时处于待机状态,完成最后一个工件加工后停机;
2) 不同的工件之间没有加工任务的优先级;
3) 每个工件的工序加工顺序不可改变,工件开始加工后不可中断;
4) 同一个资源在同一时刻只能服务一台机器,除批处理机外同一机器同一时刻只能加工一道工序;
5) 资源在机器开始加工时被占用,加工结束时进行释放;
6) 批处理过程中不能增加或减少该批次工件数目;
7) 所有工件在零时刻都可以被加工,所有机器和资源在零时刻都可以被使用。
1.2 数学模型
为建立数学模型,定义如下模型参数、决策变量、目标函数和约束条件。
1) 模型参数。
参数设置见表1。

表1 参数设置Table 1 Parameters settings
2) 决策变量。
3) 目标函数。
式(1) 表示最小最大完工时间makespan;式(2)和式(3) 表示总能耗EC,由机器加工能耗与待机能耗组成。
4) 约束条件。
式(4) 表示所有工序存在严格的加工顺序;式(5) 表示任意一个工序只能与一台机器上加工;式(6) 表示每一个工序不能属于多个批次;式 (7)表示批处理阶段的每一个批次总重量为该批次加工工件的重量之和;式 (8) 表示每一个加工的总重量不能超过批处理机的最大承受重量;式 (9) 表示批处理的最早开工时间不早于该批次中工件的前驱工序完工时间;式 (10) 表示同一时刻资源的使用量不得超过资源总数。
2 算法设计
蛙跳算法 (shuffled frog leaping algorithm,SFLA)是2003年由Eusuff等[14]提出的一种仿生物学的智能优化算法,具有概念简单、参数少、计算速度快、全局搜索寻优能力强、易于实现等特点。算法的主要步骤包括种群划分、模因组搜索和种群重构。目前,SFLA在车间调度方面有着广泛应用[15-16]。
2.1 编码与解码
对RCHFS问题,本文采用基于机器选择与工序排序的双层整数编码方式,以一组向量V=[Vj|Vm]来表示模型的一个解。第1段Vj为工序加工顺序编码,第2段Vm表示该工件对应工序可供选择的机器集中的机器顺序。解码是将矢量还原成实际问题信息的过程,为了提高算法的有效性,本文针对批处理时工件分批和资源分配两个子问题在解码过程中通过贪婪选择进行分配。
在解码过程中,机器的开始加工时间需要满足3个条件:1) 工件前驱工序完成加工;2) 指定的机器空闲;3) 指定机器所需的资源足够。本文在解码过程中首先针对向量V得到工件加工顺序与机器分配,计算前驱工序的完成时间与机器可用时间,得到最早开工时间,然后计算资源准备时间,得到实际开工时间。因此,Sij+1可以由式(11)计算得到。
其中,Tm是机器最小可用时间;TR是资源准备时间。若资源充足,则资源R将在时间段Sij+1至ETij+1被工序Oij+1占用,并在Oij+1完成后被释放,否则推迟加工,直至资源充足再加工,此时TR为资源最小等待时间,示例如图1所示。
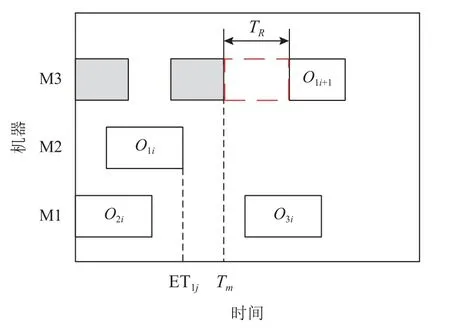
图1 解码Figure 1 Decoding
批处理阶段内有批处理机对工件进行组批加工,目前常用的批处理策略有两种。一种是阈值法,针对不同类型的工件,在未达到批处理加工阈值的情况下,将不断完成前驱工序的工件划为一个批次,直至到达批处理机的加工阈值。另一种为前瞻窗口法,针对前驱工序的完成时间和批处理机的加工阈值Q,定义窗口开始时间以及窗口大小。本文针对模型设计一种改进的前瞻窗口法,开窗时间为首先到达该批处理机的工件前驱工序完工时间,窗口大小为批处理机器的加工阈值,假设第j+1道工序为批处理工序,n个工件在批处理工序的前驱工序完工时间集合为ET={ET1j,ET2j,…,ETnj},且n个工件的工件重量和达到批处理机器加工阈值,则此时在前瞻窗口内有n个工件到达,可以形成n个方案,计算每个方案的资源准备时间并得到实际开工时间Sij+1,用两个指标评价方案的好坏,装载率与延误率。
装载率f1表示机器的利用率,计算公式为
延误率f2表示该批次工件的批处理加工阶段延误时间和的倒数,越大说明延误时间越短,计算公式为
其中,Sij+1-ETij表示工件批处理工序的前道工序的完工时间与批处理开工时间的差值。
由于量纲不同,对两个指标进行归一化处理,用于确定每个批处理批次的划分依据f。其计算公式为
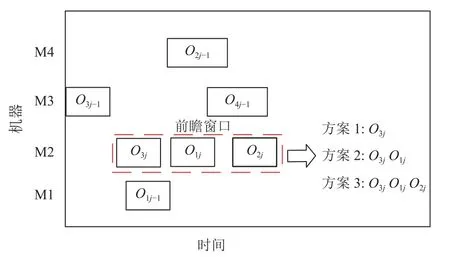
图2 分批Figure 2 Batch division
2.2 种群初始化
种群初始化是进化算法获得快速收敛速度和高效求解质量的关键。本文针对单批耦合问题,设计一种改进NEH初始化方式。具体的步骤如下。
步骤1随机生成一组基因V=[Vj|Vm],按照上文的解码方式计算每个工件的在机器上的加工时间相加得到总加工时间,按照非增顺序排列,得到初始排列ST={ST1,ST2,…,STn}。
步骤2取出前g个工件,直到在能达到批处理阶段的机器加工阈值,按原始顺序排列这部分调度,记录为当前调度,记为ST'=
步骤3取出初始排列ST中的第 (g+1) 个工件,将其插到ST'所有可能的位置,共得到g种排列,评价所有排列,将最大完工时间最小的排位,作为当前排列。
步骤4循环执行步骤3,直至输出最够调度基因。
步骤5执行步骤1~ 4,直至形成种群P。
2.3 模因组划分
对生成的初始化种群P进行非支配与拥挤度排序,按下列过程构建w个模因组:将第1个个体分到第1个模因组,第2个分到第2个模因组,以此类推,第w个分到第w个模因组,第w+1个分到第1个模因组,依次进行,直到所有个体分配完。同时为了保证搜索过程中搜索资源的充分利用,引入外部种群 Ω,容量与种群数目相同,用于保存迭代过程中被替换的较好的解。
2.4 模因组搜索
蛙跳算法主要通过模因组的搜索进行迭代跟新,通常是对所有模因组内的最差解进行优化,但是不同模因组个体的特点不同,用相同的搜索方式会忽略不同个体的特性。因此,本文将模因组分为两类,采用不同的更新策略来使其朝着最优解的可能方向进行搜索。第1类由组内存在单个目标最小值的模因组构成,第2类由其他模因组构成。通过分配给第1类模因组个体更多的搜索次数来加强算法的搜索有效性,避免搜索资源的浪费。同时加工过程中,总批次数目越少,批加工机器的利用率越高,工艺流程更为简单,所以在进行迭代更新过程尽量保留批次数目较少的解。
模因组的具体搜索过程如下。
步骤1定义模因组内搜索次数µ,最优解限制次数λ,将种群的非支配解放入外部种群 Ω,种群的每个目标的最优解为Xb1和Xb2。
步骤2将模因组进行非支配排序排序,随机选择一个非支配解为模因组内的最好解Xbb,从除Xbb外的解中随机挑选一个解作为优化对象Xb,搜索次数t=1。
步骤3对优化对象Xb与Xbb进行交叉,交叉方式采用POX与TPX两种方式,两种方式的选择概率相同,交叉生成新的个体Xbn。如果新解Xbn支配Xb,则替换解Xb;若互不支配,则判断两个解的批次总数目,保留总批次数目少的解,用另一个解更新外部种群 Ω,若为第1类模因组,执行步骤4,否则执行步骤5,t=t+1。
步骤4若新解被旧解支配,则随机选择外部解集一个解与模因组最优解Xbb生成新解Xb',如若Xb'不被Xb支配,则替换Xb且更新外部种群 Ω。若模因组组内最优解集没有进行改变,则对最优解进行邻域搜索,定义3种邻域结构,如图3所示。
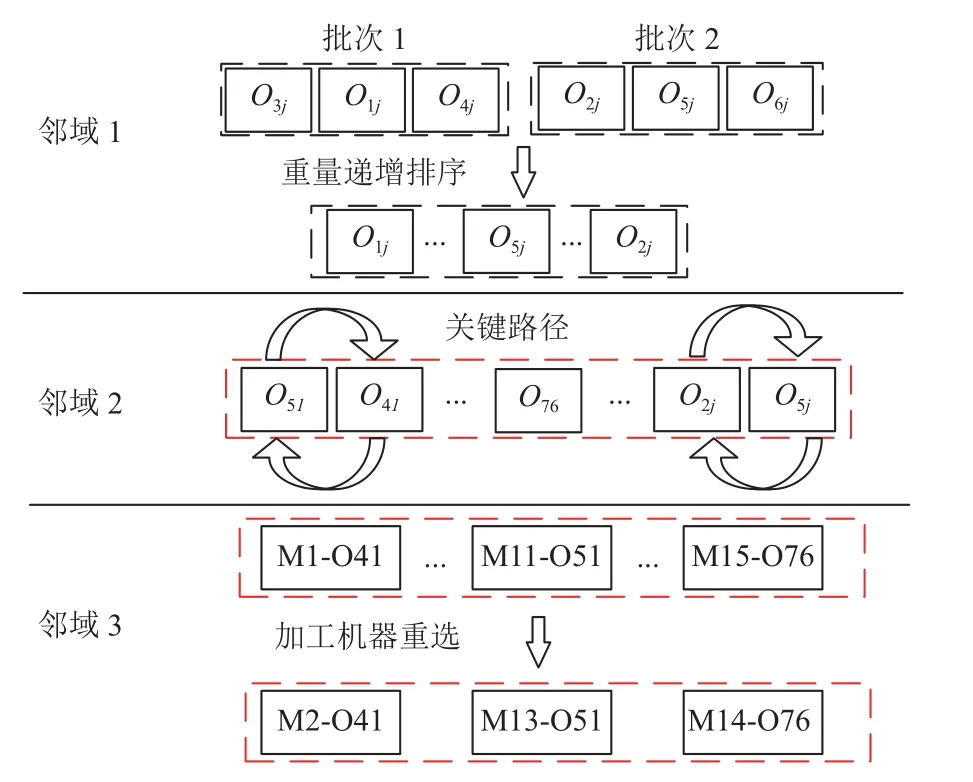
图3 邻域结构示意图Figure 3 Schematic diagram of neighborhood structure
1) 批处理工序交换邻域。随机选择若干个批次(选择批次数目不大于总批次数目),并按照工件重量升序重新分配工序位置。
2) 基于关键路径的邻域。选择一个关键路径,交换前两个与后两个关键块。
3) 资源重选邻域。随机选择若干道资源准备时间大于0的工序,为选择的工序重新分配加工机器。
步骤5若新解被旧解支配,重新生成新解Xb',如若Xb'不被Xb支配,则替换Xb且更新外部种群 Ω。若模因组组内最优解µ次没有改变,将最优解与单个目标最优值的解Xbb1或Xbb2交叉进行全局搜索。
步骤6t=µ,搜索结束。
外部种群的更新方式为:解Xb进入外部种群时,先检索是否存在相同的解,若不存在,则加入外部种群,将所有解进行Pareto排序和拥挤度,保留非支配解,剔除支配解,若数目超过外部总群容量为v,则舍弃拥挤度最小解。
2.5 算法流程
算法的流程图如图4所示,详细步骤描述如下。
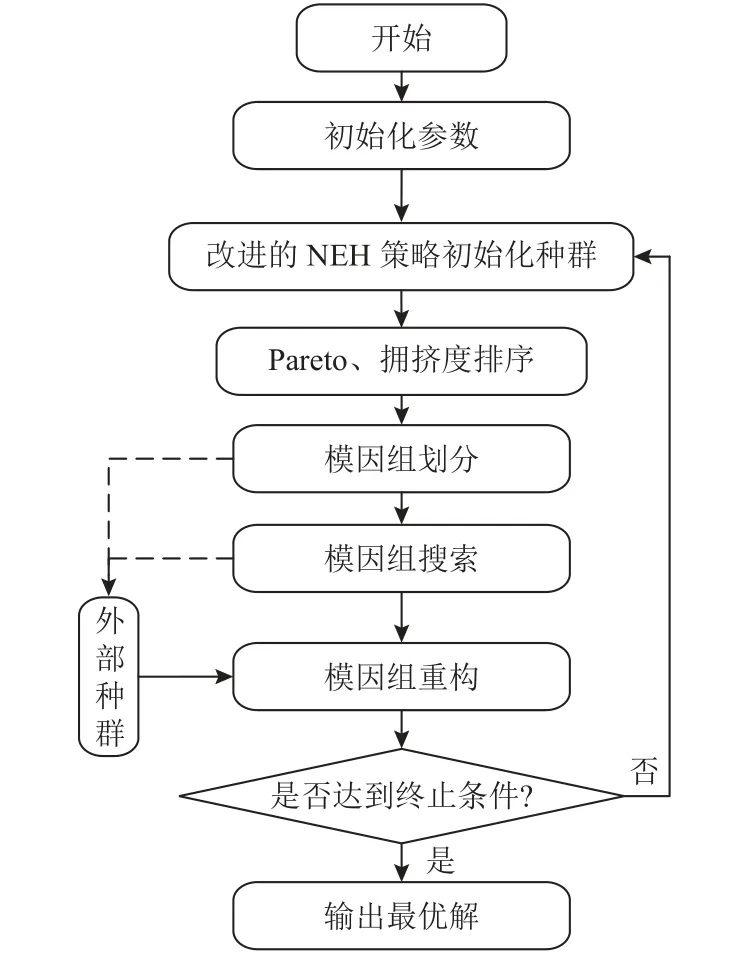
图4 算法流程图Figure 4 Flow chart of the algorithm
1) 初始化种群规模N、模因组个数w等参数。
2) 改进的NEH方法进行初始化种群。
3) 对种群进行Pareto和拥挤度排序,从而进行模因组构建。
4) 执行模因组搜索。
5) 将外部总群与模因组进行合并,重新进行Pareto和拥挤度排序,进行种群重构。
6) 判断是否达到终止条件,达到则输出种群非支配解集合,否则执行3)。
3 仿真实验
为测试算法的有效性,将参考Carlier算例[17]设计20个扩展算例和铸造企业的一组实际算例来进行仿真计算。用2个性能指标来衡量Pareto前沿。研究了每个改进措施的有效性,最后和其他的优化算法进行了对比。所有的实验在Matlab 2016上进行运行,代码的运行环境为2.7 GHz CPU,8 GB内存,64位Win10系统计算机。
3.1 测试算例和对比算法
测试算例用Carlier算例基础上扩展的20个算例和铸造企业的一组实际算例来进行仿真计算。20个扩展算例中的工件数目为 (15,30,50,100),加工阶段数目为 (4,6,8,10,12),工件重量在[10,50]上均匀分配,加工机器除了批处理阶段外,其他阶段都有3台加工机器,加工时间在[2,10]上进行分布。以算例1为例,总共有15个工件、4道工序,其中第3道工序为批处理,总共有3类加工附属资源,每种资源总数为10,另外还规定了每台机器的加工与待机能耗,机器加工所需要的附属资源数目在[1,3]上随机分配。实际算例以某批次砂型铸件为对象,该批次有12件铸件,每个工件都要进行11道加工工序,可加工机器有24台。加工流程为混砂、造型、制芯、合箱、熔炼浇筑、落砂、抛丸、打磨、机加工、清整及出库检查,其中第5道工序熔炼浇注为批处理工序阶段,其他工序为单加工工序;加工附属资源数目为4种,分别为在造型与制芯工序的砂箱,在熔炼浇筑阶段需要的保温炉,熔炼、混砂、抛丸、落砂需要的除尘设备与工序之间的运输设备。
为说明算法的有效性,选择在车间调度问题中常用的非支配排序遗传算法 (non-dominated sorting genetic algorithm,NSGAⅡ)、帝国竞争算法(imperialist competitive algorithm,ICA)[18]以及灰狼算法 (grey wolf optimizer,GWO)[19]作为对比算法。其中NSGAⅡ的交叉率为0.7,变异率为0.3,其余算法参数与算法参考文献一致,对比算法采用随机编码的方式进行种群初始化。为验证算法的有效性和避免结果的随机性,每个算例下的算法独立运行30次,结果采用30次运行的平均值。
3.2 评价指标与实验参数
为了综合评价算法的收敛性和稳定性,用两个指标来评价算法的性能。
1) IGD指标,等同于衡量算法的收敛性和多样性,值越小,收敛性和多样性越好,计算公式为
其中,di表示欧氏距离,PF为参考集。
2) RAS目标完成率,计算同时达到每个目标的概率,越小说明解质量越好,计算公式为
其中Ui是每个目标的最小值。
算法的主要参数有3个:种群规模N,模因组数目w,模因组内搜索次数µ。采用实验设计考察不同的参数对算法性能的影响,以“J15-10b8”为测试算例,选择规模为 (33) 的正交试验对算法参数进行优化,为避免结果的随机性,每组算法独立运行30次,取IGD值作为评价指标,实验结果如表2所示。根据正交试验表绘制如图5所示的参数水平趋势图,由图可以确定本文算法的参数选择种群规模N=90,模因组数目w=10和模因组内搜索次数µ=30,此外算法运行时间取1.8×103s。

图5 参数水平变化趋势图Figure 5 Trends of parameter levels

表2 正交试验结果表Table 2 Results of orthogonal test
3.3 计算结果与分析
3.3.1 扩展算例结果分析
20个测试算例的比较结果见表3和表4,其中粗体表示各算例算法所得最优值。从表3给出的20个算例仿真结果在最小化最大完工时间、机器总能耗两个目标值上来看,在规模较小的算例中,算法的目标平均值差距不大,随着算例规模的增加,本文所提出的算法所求结果明显优于其他算法,在较多算例上能得到最低的平均值。从表4给出的不同算例下算法性能指标来看,在规模较小时,NSGAⅡ和ICA能得到较低的IGD与RAS值,但综合来看ISFLA在获得较好IGD值的同时,能减小RAS值,说明算法得到的解能更好地接近最优解,因此综合分析所提算法具有明显的优越性。

表3 算例仿真结果对比Table 3 Comparison of simulation results of calculation examples
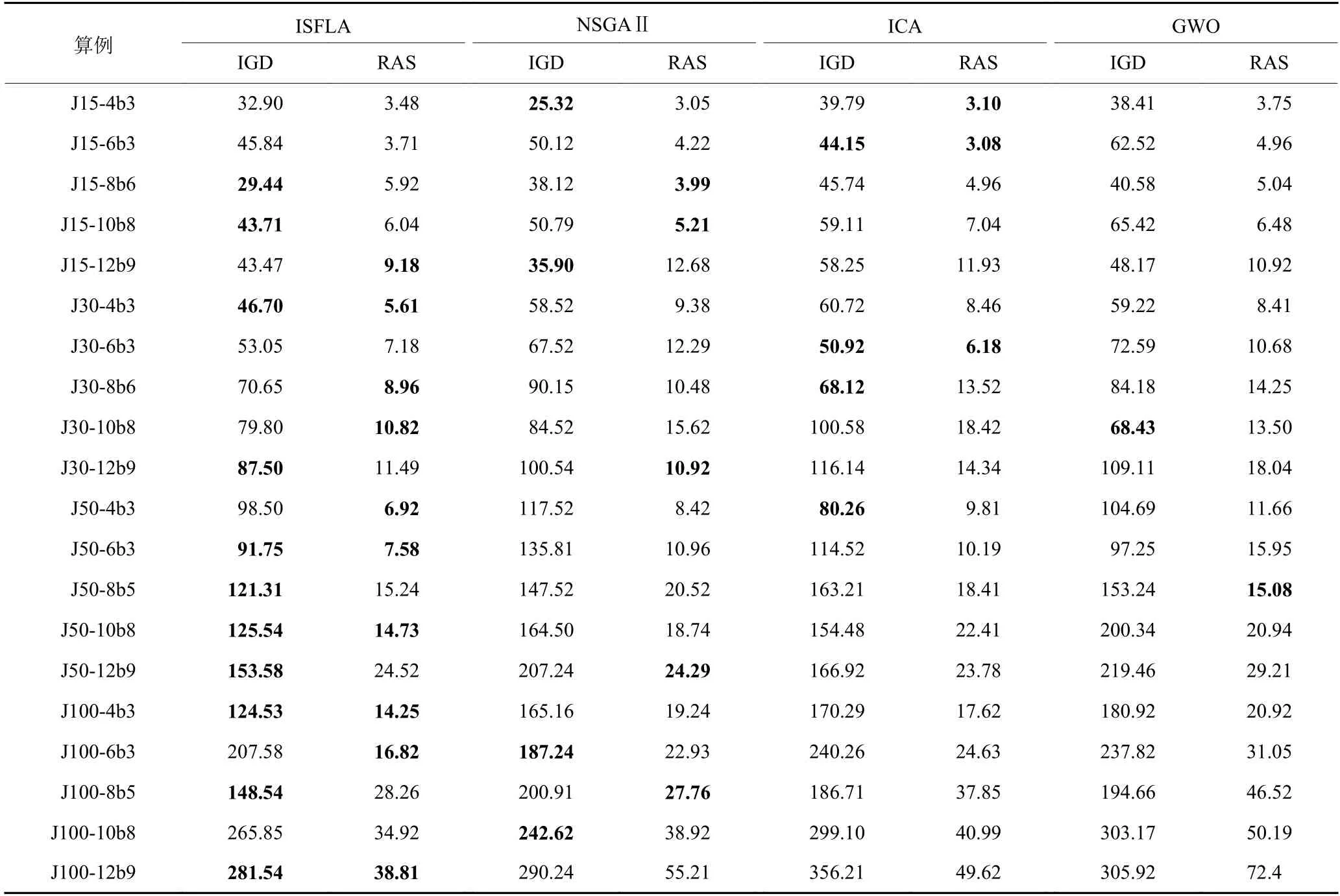
表4 算例仿真指标对比Table 4 Comparison of simulation indicators of calculation examples
3.3.2 实际算例结果分析
为了更好地体现算法的实用性,使用某砂型铸造企业的一组实际加工订单作为实际案例来验证算法的有效性,在砂型铸造生产流程中主要分为铸造前阶段,熔炼浇筑和铸造后处理3个阶段。图6为4种算法的目标值随着时间变化的收敛曲线,图6 (a)与图6 (b) 分别展示了最小完工时间与机器总能耗随着运行时间的迭代图,从图中可以看出,ISFLA算法收敛性最好。由于ISFLA算法采用了本文提出的初始化策略和更适应模型的解码方式,因此初始种群的质量较其他几种算法更好,同时算法采用改进的模因组搜索方式,因此能更好地收敛到最优解。图7为该实际算例求得的一组解中的序号最前的调度甘特图,图中矩形的每种颜色表示一个工件,数字表示加工阶段,例如1 203可以描述为工件J12的第3个加工阶。该算例中工序5为批处理工序,从图中可以看出工件被分为4个批次,由批处理机M12与M13进行加工,经优化后其最大完工时间为195 min。
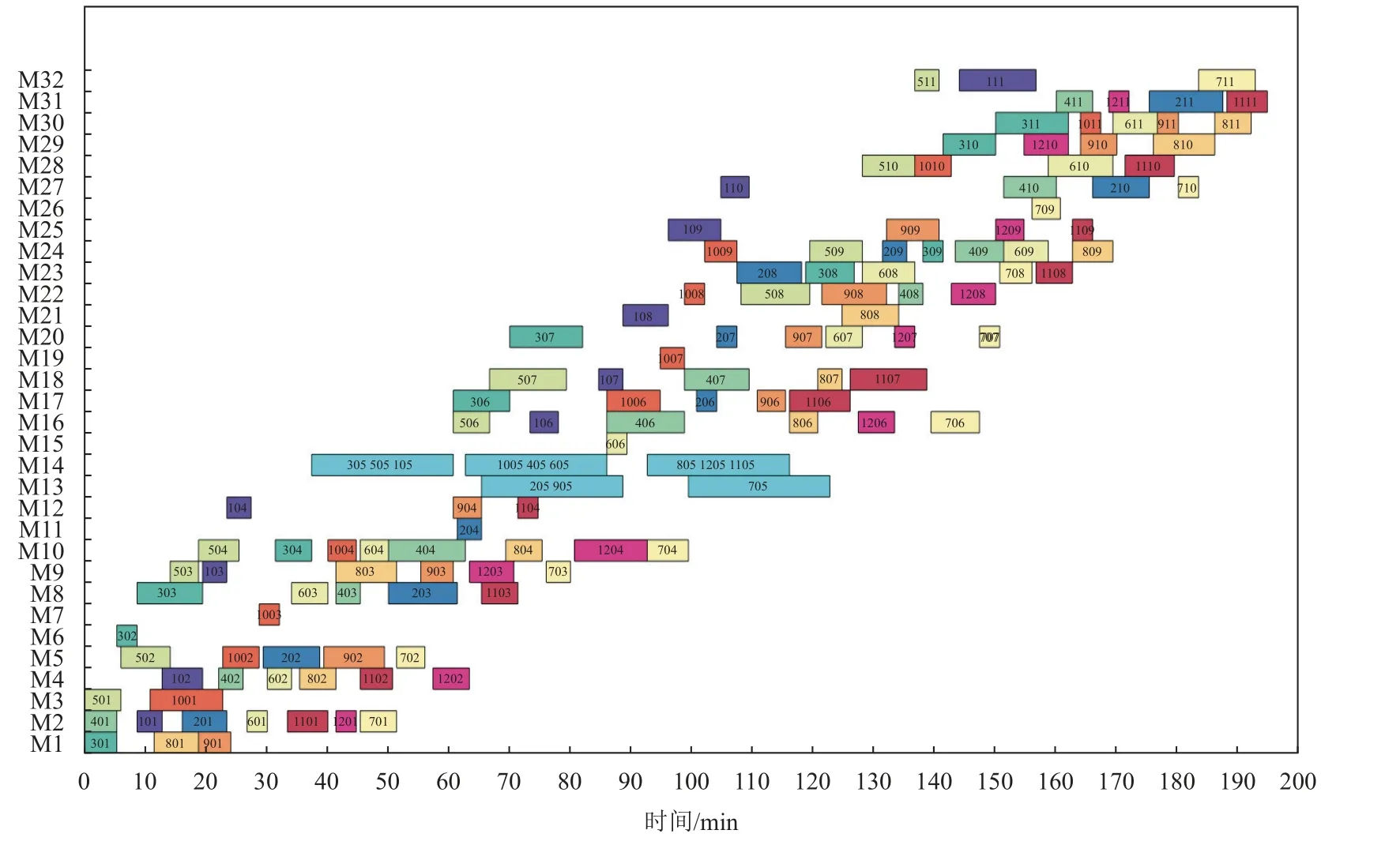
图7 调度甘特图Figure 7 The scheduling Gantt chart
4 结论
本文以资源受限下的混合流水车间为对象,针对资源约束和单批耦合特征,建立了以最大完工时间和机器能耗为目标的数学模型。提出一种改进的离散蛙跳算法,在蛙跳算法的基础上增加了一种改进的NEH初始化策略,提高了初始种群质量,改进了模因组的进化方式并增加了外部种群,增加了算法的全局搜索能力和局部搜索能力。最后通过扩展算例与实际算例验证了算法的可行性与有效性。
但是本文未考虑动态因素与分布式生产的影响,在未来的研究中,重点可以放在动态约束与分布式生产上。此外,将深度学习、强化学习和大数据分析与车间调度结合也是一个重要的研究方向。

