面向众包平台的偏好和结构相似度融合式设计团队发现

刘电霆，吴珊，赵思佳，尚磊，叶恒舟

(桂林理工大学 1.机械与控制工程学院；2.信息科学与工程学院，广西 桂林 541004)

众包[1]作为一种新兴群体协作的模式在各个行业得到广泛的应用，并有了许多成功的案例[2]，如InnoCentive平台、Kaggle网络众包竞赛平台、威客平台等。随着互联网的飞速发展，网络众包以低成本将地理分布广泛、文化差别巨大的多个不同创新源汇聚到同一个开放平台。面向产品创新设计时，在执行协作型众包 (collaborative crowdsourcing) 设计任务的过程中，常常涉及多个领域的专业知识，需要许多具有不同技术水平的设计者组成团队参与其中[3]。

在众包设计平台下，设计人员偏好是指其自身主观意愿和选择所表现出不同行为，发包方与接包方在交互过程中的需求和意愿信息能表达设计人员的偏好。当设计人员分配到符合自身意愿和擅长技能的任务时，其积极性和任务的完成质量通常会得到提高。在众包环境下，平台对设计人员的兴趣偏好以及历史行为活动进行梳理，能有效增加任务分配的准确性，即利于找到合适的设计人员或设计团队，以提高设计任务完成的质量。

目前，有许多学者研究设计人员偏好问题，但主要是针对单个众包任务、考虑单个设计人员的兴趣偏好。潘仁志等[4]提出一种基于卷积神经网络交互的用户属性偏好建模的推荐模型 (UAMC)，从用户的不同属性对不同项目的偏好学习到用户更准确的潜在向量。王晓燕等[5]通过用户—任务关系评价兴趣度值的方法并结合用户浏览内容及历史完成记录来建立用户兴趣模型。武聪等[6]提出一种融合用户标签相似度的矩阵分解算法，更准确地了解用户的偏好。Horvath[7]引入3个学习任务 (精确性、顺序性以及迭代性) 对用户属性特征进行挖掘，并用于偏好学习。Lin等[8]结合隐式的反馈信息来提取用户的兴趣偏好。

但是，在复杂产品众包设计项目中，往往需要组建团队来完成相关任务。这要用到团队发现方法，按是否利用先验知识，可将其分为无监督、半监督或有监督学习等类型。现有方法在组建团队时，一般利用无监督技术来确定设计成员属性的权重或将所有可用属性视为同等重要。Gunnemann等[9]就提出一种无监督的谱权重聚类方法，用来检测每个团队的相关属性子集，并构建团队结构。姜东明等[10]提出一种基于图卷积网络模型的无监督团队检测算法，将半监督学习方法扩展到非监督学习领域。而半监督或有监督型团队发现方法，考虑用户给定的约束，挖掘到的团队内部节点一般是受用户偏好控制的。Wu等[11]提出一种在目标子空间中挖掘目标团队的方法，它是根据用户提供的两个样本节点扩展到一组样本节点，从而推导出目标属性权重并挖掘目标团队的集合。孟彩霞等[12]提出一种基于节点重要性和节点相似性的改进标签传播算法(CRJ-LPA) 提高团队结构划分的质量，还在一定程度上克服了传统标签传播算法的随机性。王静红等[13]提出一种基于节点相似度的半监督团队发现算法(SSGN)，比其他半监督聚类算法更准确、高效。杨晓光等[14]对现有团队发现算法准确度较低的问题，提出了一种基于中心节点的团队发现算法，提高了团队发现的准确度。然而，现有半监督或有监督团队发现的聚类技术和标签传播算法虽然考虑了用户的偏好，但在聚类过程中一般都是只利用节点的部分属性或者是仅考虑节点的属性信息[15]。上述的这些方法，主要是从成员属性角度来考虑团队的组建。

随着计算机技术的发展，陆续出现其他的团队发现算法。其中，Louvain算法是一种基于模块度的团队发现算法，被认为是效率最快的算法之一。Louvain算法整体上分为两个阶段：在阶段1中将相似的节点归为一类，在阶段2中将同一类的节点合并为一个大的聚合节点，然后重复阶段1。目前，不少学者利用Louvain算法进行团队发现，主要关注所发现团队的质量或算法的效率。褚叶祺等[16]利用Louvain算法对C-DBLP作者发文合作关系的数据进行了团队划分，有效地揭示了各个学科之间不同的合作交流模式，但仅考虑了节点之间的链接度。吴祖峰等[17]针对设计者网络中出现的叶子节点进行剪枝处理，提高Louvain算法的运行效率。但是，基于模块度的团队发现方法考虑的是网络成员之间的连接关系。

针对上述问题，本文综合考虑团队成员兴趣各不相同的因素等属性，利用改进模块度的S_Louvain算法对团队成员偏好和结构相似度进行融合，从而提高团队的可靠性和连结性，促进众包任务的成功完成。

1 相关定义

记网络G={V,E,F} 为属性图，其中V={υ1,υ2,···,υn}表 示网络中节点的集合，n为节点数；E={e11,e12,···,enn}表 示节点与节点之间的关系，若节点 υi和υj之间存在连边，则eij=1，否则eij=0；F={f1,f2,···,fr}表示节点的属性集，对于给定节点 υ ∈V，其属性列向量可表示为f(υ)=[fυ1,fυ2,···,fυr]T。

1.1 偏好相似度

设计者节点的偏好归于属性范畴，其相关的属性值反映了节点的偏好，常用自然语言的词语来表达。而词向量 (word embedding) 作为自然语言处理(NLP) 中重要的基础，为数据中文本、情感、词义等方面的分析提供了有力的帮助。词向量主要是将词转化为稠密的向量，使相似的词，其对应的词向量也相近。在本文中，利用它将设计者偏好的属性特征转化为向量形式，从而计算设计者间偏好的属性相似度。对于给定设计者节点u和 υ偏好的属性相似度计算公式为

其中，∥f(u)-f(υ)∥表 示节点u、υ偏好的属性列向量的差值二范式；R(u,υ)的取值范围在[0,1]之间。

1.2 结构相似度

考虑网络节点的拓扑关系时，Jaccard相似度常用于比较两个样本集之间的相似性和差异性，且易于计算。参照Jaccard相似度的计算方法，对于给定节点u和 υ 的结构相似度计算公式为

其中，G(u)表 示节点u的邻居节点集合；G(υ)表示节点 υ的邻居节点集合；J(u,υ)的取值范围在[0,1]之间。Jaccard值越大，说明两个节点之间的结构相似度越高。

1.3 模块度

模块度是Newman[18]提出来用以衡量一个网络团队划分结果的指标。对于一个理想化的划分结果，其表现形式为在团队内部节点的链接度尽可能的高，与团队外部节点的链接度尽可能低，即团队划分质量越高对应的模块度Q越大。Q的取值范围在[-0.5,1) 之间。研究表明，当Q的值在0.3～ 0.7之间时，说明团队划分的效果较好。模块度Q可表示为

其中，∑in表 示团队c内的边的权重之和；m表示网络的总边数；∑ tot表 示团队c与其他团队连边的权重和。

Newman[18]将模块度Q的概念嵌入到网络社团划分中，但该方法仅考虑了团队成员与邻居节点的关系，而忽略了团队内成员的偏好相似度等属性。按其方法，若一位成员与某团队内成员没有连边关系，即使其与该团队内成员的偏好相似度极高也不会被纳入到该团队中，这显然不太合理。

1.4 Louvain算法

Louvain算法是一种基于模块度优化的团体发现算法，是目前公认速度较快、效率较高的团队检测算法之一。该算法可被划分为节点的局部移动和网络团队聚合两个阶段[19]。首先将每个用户节点看成一个单独的团体，并对其做标识。对于每个节点i，找到其全部邻居节点，分别计算若将节点i从当前所在团体移至其邻居节点j所在的团体，所产生的模块度增益的大小 ∆Q。若m ax∆Q大于0，则将节点i加入到节点j所在的团体，否则节点i仍保持在原来的团体。依次迭代上述步骤，直至所有节点所属的团队不再变化。然后初始化整个图，将分区中的每个团体称为聚合网络中的聚合节点，按照上一阶段的方式进行迭代归类，直到团队之间不能再合并为止。

虽然Louvain算法速度较快且思想简单，但是如果团队过大会导致不能及时收敛，即团队在聚类的过程中没能及时收敛。因为Louvain算法是针对节点进行遍历的，容易将一些外围的节点加入到原本紧凑的团队中，从而导致一些错误的合并。其中，一个关键问题是Louvain算法是一种基于模块度的团队发现方法，即主要依据成员之间的链接关系，而没有考虑成员之间的偏好相似度等属性。

2 偏好和结构相似度融合Louvain算法的团队发现方法

2.1 方法概述

为了解决传统团队发现方法主要偏重成员之间的偏好相似度属性，而没有将其与成员之间的结构相似度结合考虑，或从团队模块度出发仅考虑团队成员与邻居节点的链接关系，而忽略成员之间的偏好相似度等属性的问题，本文在传统Louvain算法基础上，综合考虑团队成员的偏好相似度和结构相似度来选择有一定关联、有可能组成团队的候选节点集，并提出一种新的基于偏好相似度的模块度函数，从而避免了没有边连接的成员被遗漏在所划入团队之外的问题，在一定程度上提高了团队划分的准确度。

2.1.1 目标团队候选节点采集

在社会关系中，考虑节点的结构相似性时，如共同邻居越多，则成员具有相同类别的可能性越大；但是仅考虑成员之间在网络拓扑中的结构相似性并不全面，成员之间由于存在偏好不同也有可能导致其类别不同，从而需要将其划归为不同的团队。因此，在组建团队时需要综合考虑节点的偏好相似度和结构相似度，这样组建的团队则更加紧凑，团队内部信息流通更快。本文结合1.1小节和1.2小节中节点的偏好相似度和结构相似度来挖掘候选节点集。考虑团队成员之间的综合相似度，具体计算公式为

其中，wR和wJ分别为偏好相似度和结构相似度的权重。

对于给定网络图G={V,E,F}，本文以用户给定的设计者节点作为目标团队的种子节点，从而扩展得到候选节点集。初始化目标团队候选节点Z={z}，具体计算公式为

其中，β为相似度阈值；一般来说，可以认为偏好相似度和结构相似度同等重要，即权值wR和wJ都取0.5。然后，根据式 (5) 扩展可以得到团队的候选节点集Z={z1,z2,···,zc}。其中，c表示候选节点集的节点个数。

2.1.2 改进的模块度函数

传统Louvain算法是一种基于模块度的团队发现算法，而其常用的模块度计算仅考虑团队成员与邻居节点的链接关系，可能导致偏好属性相同但没有边连接的成员被遗漏在所划入团队之外的问题。为此本文考虑成员的偏好相似度，对传统Louvain算法的模块度函数进行改进，具体计算公式为

其中，S表示所有节点偏好的属性相似度之和；Rij表示节点i和节点j的偏好的属性相似度。

2.2 S_Louvain算法描述

本文在给定图G={V,E,F}的基础上，先按式 (1)和式 (2) 分别计算所有节点的属性相似度和结构相似度；并通过式 (4) 计算节点的综合相似度；再通过式 (5) 计算候选节点集，将候选节点集运用到团队划分的过程中；然后，通过式 (6) 的模块度函数来更新优化团队，直到所有节点的所属团队不再变化为止，得到团队划分的最后结果。

算法具体流程如下。

1) 将图中每个节点看成一个独立的团体，此时团体总数等于节点总数。

2) 对于非种子节点i，计算其邻居节点所属团队的模块度增益，若其邻居节点团队中含有种子节点且这些团队的 max∆Q＞0，则优先将节点i移动到与max∆Q相对应的团队中；否则计算将其移动到不含种子节点团队的m ax∆Q，如果此m ax∆Q＞0，则将节点i移动到与 max∆Q相对应的团队中；如果不满足上述情况，则节点i隶属的团队保持不变。种子节点之间不合并。

3) 迭代流程2)，直到所有节点的所属团体不再变化。

4) 对各个团体所有的节点进行压缩，使其成为一个新的聚合节点，团体内节点权重转化为新聚合节点的环权重，团体间的权重转化为新聚合节点边的权重。

5) 重复流程1) 到流程4)，直至整个网络的模块度不再发生变化。

2.3 时间复杂度分析

本文提出的偏好和结构相似度融合的团队发现方法，即在整个网络中计算所有节点的偏好相似度和结构相似度，并通过式 (5) 扩展得到候选节点集；利用候选节点集，按式 (6) 的改进模块度函数来更新优化设计团队。算法的时间复杂度包括3阶段：第1阶段为计算节点的偏好相似度和结构相似度的时间开销；第2阶段为计算候选节点集的时间开销；第3阶段为更新优化团队划分的时间开销。

记网络G={V,E,F} 的节点为n，边数为m，第1阶段计算图中节点与节点之间的偏好相似度和结构相似度所需的时间为O(n2)，第2阶段计算候选节点集的时间为O(n)，第3阶段团队划分所需时间为O(nc+n′c)。其中，c为移动一个节点所需的时间；n′为聚合后的节点个数。本文算法的整体时间复杂度如表1所示。

表1 算法运行各阶段时间复杂度Table 1 Time complexity at each stage of the algorithm

3 实例分析

为了验证上述方法的有效性及实用性，分别在两个公开数据集以及工程实例上进行实验。首先，对算法过程进行描述，然后对实验所用到的公开数据集和众包工程实例数据集进行描述。最后将本文算法与改进前的算法进行对比分析。

3.1 数据集

3.1.1 公开数据集

选取了Polbooks数据集和MovieLens数据集进行验证。Polbooks是由在线书商Amazon出售的关于美国政治的书籍网络，其中节点代表书籍，边代表同一个用户购买了这两本书，属性代表书籍的资料信息。MovieLens是经典的电影评分数据集，根据其大小不同可分为3个不同的版本[20]。本文采用MovieLens-25M数据集，该数据集中节点代表电影，边代表共同看过该电影的用户，属性代表电影的主题信息。预处理后的真实数据信息详情见表2。

表2 真实数据集Table 2 The real dataset

3.1.2 众包工程实例数据集

由于设计人员的数据搜集难度较大，本文整理了某众包平台工业智造领域的150名设计用户，针对他们测试S_Louvain算法，来体现该算法的实用性。该数据集的节点代表设计人员，边代表用户的专业领域，属性则为设计人员的兴趣偏好 (即设计用户完成的历史任务类型)；从众包平台上可查询到设计用户完成的历史任务，获取设计用户的兴趣爱好，具体用户 (选取数据中的10位设计用户) 兴趣偏好见表3。

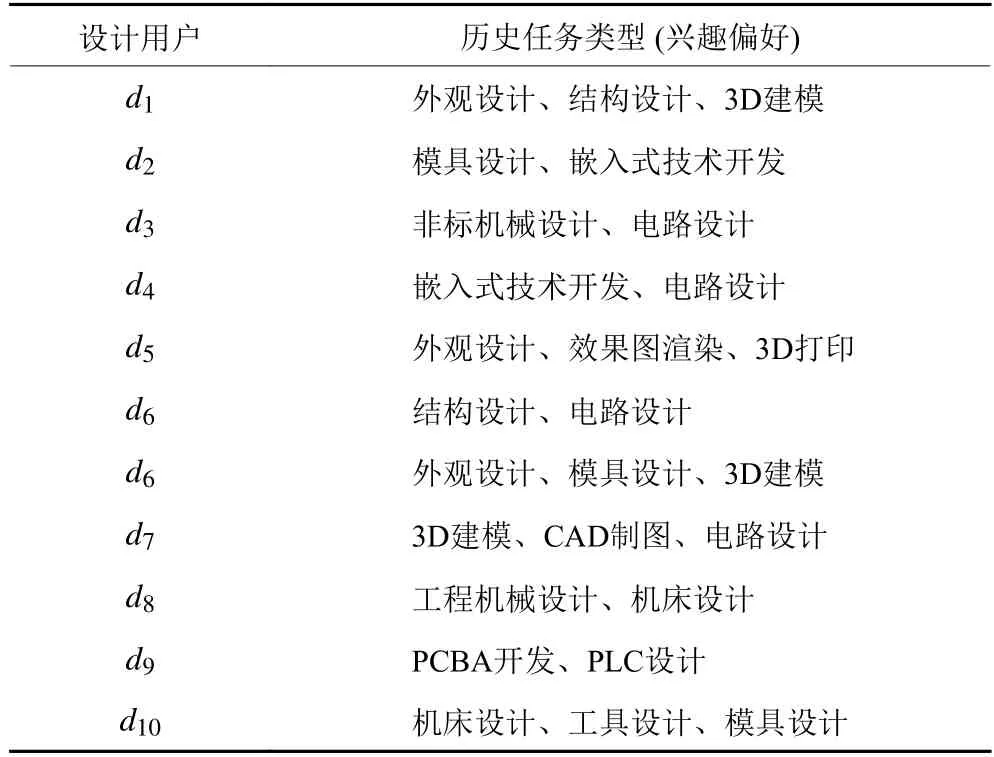
表3 设计用户的兴趣偏好Table 3 Interests and preferences of design users

其中，这150名设计用户所涉及的兴趣偏好总数为77种，所涉及领域可分为产品设计、机械设计、模具设计制造、智能产品设计、3D建模与打印、电路设计、嵌入式开发、电力电子开发、智能解决方案、生产采购、制造自动化等领域。

3.2 结果对比

为了验证本文方法的有效性，以模块度指标作为衡量标准，在传统Louvain算法和S_Louvain算法上进行比较，具体结果如表4和图1所示。图2～ 4分别为3个数据集在S_Louvain算法上得到的划分结果，其中，颜色相同代表属于同一团队的成员，不同颜色代表属于不同团队的成员。

图1 不同算法在数据集上的Q 值比较Figure 1 Comparison of Q values of different algorithms on datasets

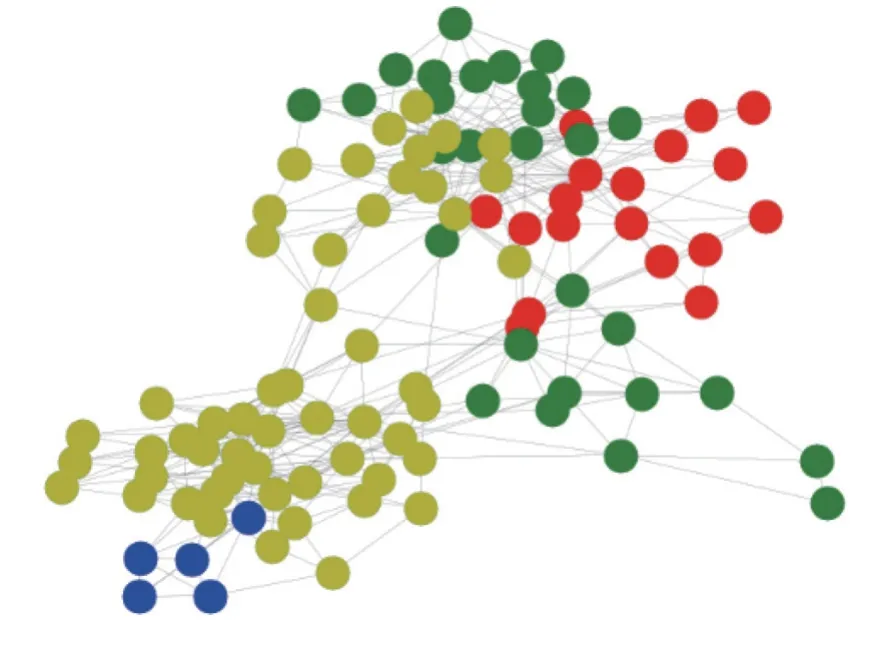
图2 S_Louvain算法在polbooks数据集上的分类结果Figure 2 Classification results of S_Louvain algorithm on polbooks datasets

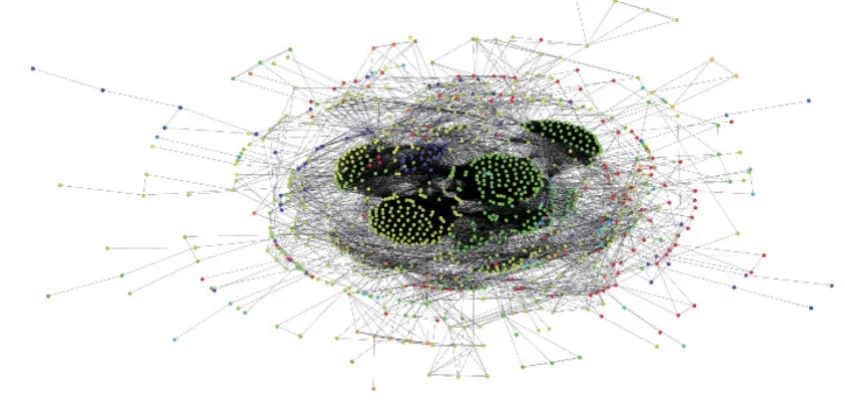
图3 S_Louvain算法在movieLens数据集上的分类结果Figure 3 Classification results of S_Louvain algorithm on movieLens datasets

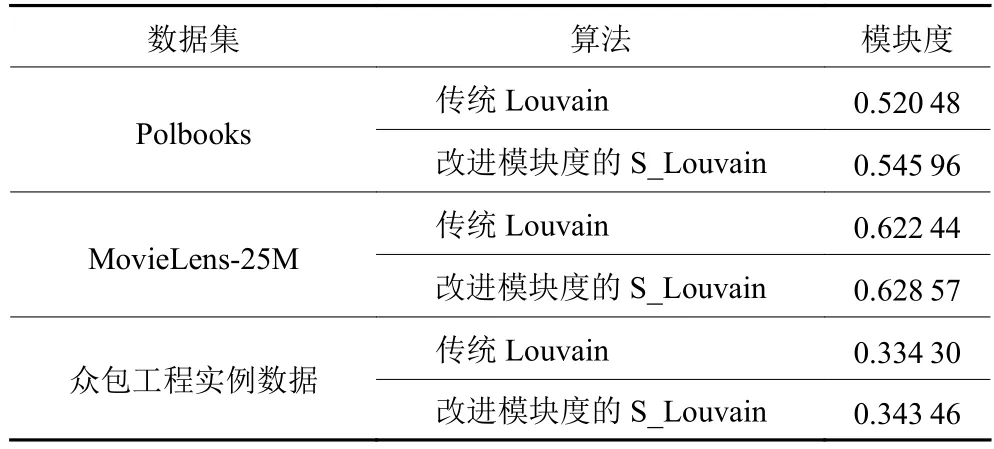
表4 方法对比Table 4 Comparison of methods

由表4中的结果可知，相比于传统Louvain算法，改进模块度的S_Louvain算法在Polbooks数据集上模块度指标增加了4.895%，MovieLens-25M数据集上模块度指标增加了0.613%，众包工程实例数据集上模块度增加了2.740%。图1清晰地展示了本文所提的算法和对比算法模块度Q的比较。图2～4显示了3个数据集在本文算法上的团队划分结果。由图4的团队划分结果可视化可知，150名设计人员被算法S_Louvain很好地划分为5个团队。

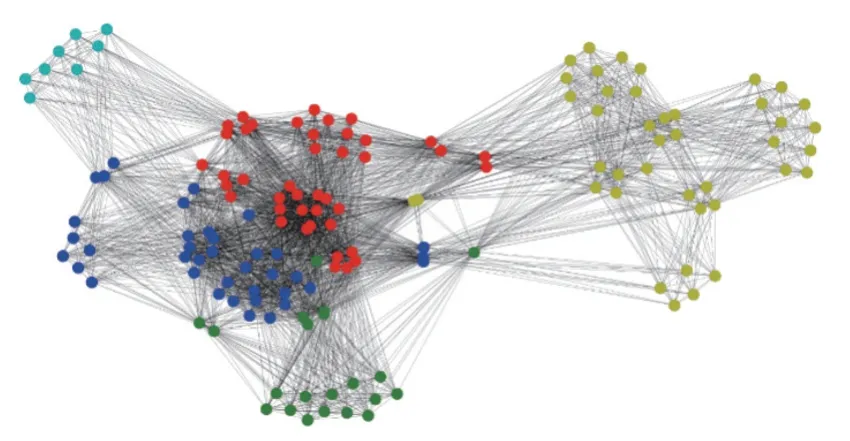
图4 S_Louvain算法在众包数据集上的分类结果Figure 4 Classification results of S_Louvain algorithm on crowdsourced datasets

测试结果表示，无论是在公开数据集上还是众包工程实例数据集上，改进模块度的S_Louvain算法都能在一定程度上提高团队内成员之间的连结强度，即模块度，且综合考虑团队成员的兴趣偏好，能更好地为团队分配合适的众包任务。

4 结论

针对众包平台在组建团队过程中存在成员偏好不一的问题，提出一种改进模块度指标策略的S_Louvain算法。该算法相比传统Louvain算法，在迭代更新模块度增益的步骤中充分考虑了众包团队成员之间的兴趣偏好相似度以及结构相似度，能使组建的团队之间具有更强的连接度。为验证所提算法的可行性和实用性，分别在公开数据集和众包工程实例数据集上进行试验。实验结果表明，S_Louvain算法在polbooks数据集上模块度指标提升4.895%，在工程实例数据集上，模块度指标提升2.740%；S_Louvain算法在模块度指标上均得到提高，在一定程度上加强了团队内成员之间的连结强度。这说明S_Louvain算法可用于解决众包平台团队组建中的成员偏好融合问题上。在下一步的工作中，将研究如何将协作设计众包任务模块推荐给众包团队，进一步提高众包任务完成的效率以及成功率。