基于过程识别的认知性VDT监控作业绩效形成机理

黄琨，廖斌

(1.四川城市职业学院 信息技术学院，四川 成都 610101；2.四川师范大学 商学院，四川 成都 610101)

监控作业是核电站、化工厂、空中交通管制中心等场所的常见工作形式，信息化的深入正促使传统的模拟式监控向数字化监控转变。数字化控制室中，计算机及控制软件终端成为作业人员的“工具机”[1]。“工具机”通常以视频显示终端 (visual display terminal，VDT) 的形式呈现[2]，VDT监控作业已成为数字化控制室的主要劳动形式。VDT监控作业分为“简单判断型”和“认知型”两类，后者 (认知性VDT监控作业) 的应用越来越普遍，它要求作业者持续注视显示终端获取信息，通过大脑处理后完成输出[3]。由于计算机信息处理技术的不断提高，人的可靠性已成为认知性VDT监控作业系统绩效薄弱环节的重要组成部分[4]，如何提高人的绩效水平成为当前亟待解决的重要社会问题。

另一方面，科学管理最基本的逻辑是通过过程控制实现管理目标，Gilbraith通过“动素”分解各种体力作业过程，极大提高了劳动者的作业绩效[5]。认知性VDT监控作业属于内隐性脑力劳动，目前相关学者主要从认知负荷识别[6-7]、监控任务特征[6,8]、作业时间制度[9]、作业环境改善[10-11]等外显属性展开研究，从过程解析视角进行的作业绩效改善研究还很少见。

基于此，本文将在笔者近期研究成果[2]的基础上，运用隐马尔可夫模型 (hidden Markov model，HMM) 解码认知性VDT监控作业的隐状态过程，通过分析3种难度水平下作业过程及绩效的差异，探究绩效的形成机理，以期为从过程解析视角改善认知性VDT监控作业绩效提供理论依据。

1 认知性VDT监控作业的HMM结构分析

HMM是一种描述随机过程的概率模型，对于复杂时间序列具有很好的建模能力[12]。隐马尔可夫过程中状态是不可观测的，可观测到的只是这些状态所表现出来的观察量[12]。

1.1 隐状态集合

文献[2]提出，认知性VDT作业过程可以通过元认知、信息辨识等13个认知动素 (cognitive therbligs，CT) 解析，将这13个认知动素设为认知性VDT监控作业隐马尔可夫过程的状态集合S={s1,s2,···,s13}，见表1。根据人的信息处理阶段模型理论[13]，认知性VDT作业过程中某时刻的信息处理状态取决于前时刻的作业状态。

表1 认知性VDT监控作业状态集Table 1 State set of a cognitive VDT monitoring operation

1.2 观察指标体系

认知性VDT监控作业的过程状态不可观测，但是这些状态下的各种生理参数是可观测的。

眼动追踪技术是研究认知心理学的重要工具[14]。个体的眼动行为是自发的，眼动指标具有良好的生态效度和时空分辨率，能真实反映个体认知过程特征[15]，具有很好的实时性、无干扰性和可操作性。针对认知性VDT监控作业，作业者任意时刻的眼动观测结果取决于该时刻的作业状态，与其他时刻的观测及状态无关。基于此，本课题将选择眼动生理参数作为认知性VDT监控作业过程的观察集。

Luke等[16]研究发现，在阅读、视觉搜索和场景观看时，对工作记忆量要求越大的任务，被试者的眼跳幅度 (saccade range，SR) 就越小，长注视的比例越高；Henderson等[17]认为认知过程中，人的注视时间 (fixation time，FT) 分布特点与大脑皮层的眼动控制网络 (顶内沟、额下回等区域) 存在关联。Joshi等[18]提出蓝斑是大脑合成和释放去甲肾上腺素的主要中枢，能调节大脑注意系统的运作，瞳孔直径(pupil diameter，PD) 的变化与蓝斑的活动存在共变性，瞳孔直径是人类认知活动中反映注意资源分配的有效指标；Hayes等[19]研究任务状态下个体认知活动诱发的瞳孔反应，发现探索型问题导致的瞳孔扩张显著大于规则运用型问题。可见，SR、FT、PD是研究人类认知问题的有效眼动指标。

本研究将SR、FT、PD设为认知性VDT监控作业隐马尔可夫过程的观察指标，然后设计试验，采集3个观察指标的时序数据，通过聚类分析构建观察集合V={v1,v2,···,vm}。

1.3 隐马尔可夫过程概念模型

考虑认知性VDT监控作业过程中的状态转移特征及眼动观察结果独立性，结合前文提出的状态集合S和观察集合V，构建认知性VDT监控作业的隐马尔可夫过程概念模型，如图1所示。

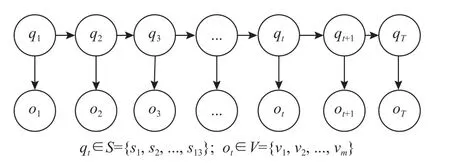
图1 隐马尔可夫过程概念模型Figure 1 Conceptual model of hidden Markov process

模型表明，每次作业过程均会产生1个内隐的状态序列Q=[q1,q2,···,qT]，qt∈S={s1,s2,···,s13}；对应这个状态序列，会产生1个外显观察序列O=[o1,o2,···,oT]，ot∈V={v1,v2,···,vm}。状态序列和观察序列共同描述某次作业过程，过程特征可以用参数λ=[A,B,π]表示。

式中，aij=Pr(si/sj)，表示状态si转移到状态sj的概率。

式中，bj(k)=Pr[sj(ok)]，表示状态sj下产生ok的概率。

式中，π为初始状态矢量，ci为初始状态q1=si的概率。

2 试验方法

2.1 试验设计

根据N-back范式设计心算监控任务，任务由9个trial构成，通过E-Prime2.0编程实现。每个trail从屏幕中间呈现提示符“+”开始，然后依次呈现4个整数 (按呈现顺序，依次设为T1、T2、T3、T4，T1、T2、T3、T4∈[1,9])，最后在探测界面呈现心算任务。任务要求被试者记忆之前呈现4个数字中的2个，完成心算 (加法/减法) 并判断等式正误，比如，T1+T3=5，如果等式正确单击“Enter”键，错误则单击“Space”键。单trial呈现方式见图2。

图2 单trail呈现方式Figure 2 Presentation of a single trail

N-back范式中“N”指以探测界面为起点，按数字T1、T2、T3、T4呈现时序倒数的步数，T4:N=1，T3:N=2，T2:N=3，T1:N=4。N越大则记忆难度越大。设心算任务中2个待运算数字对应的N的和为SN，根据SN的大小确 定3个难度水 平Di(i=1,2,3)，分别为D1:SN=3，D2:SN=4，D3:SN=5。每个难度水平设计3个trial，任务包括3个难度水平，共9个trial，随机呈现。被试者对试验变量的设置不知情。

因此，试验以难度水平为自变量 (被试内)，被试者在探测界面的正确反应时间 (correct response time，CRT) 为因变量 (作业绩效指标)。

2.2 被试者

在学校的本科生及研究生中甄选被试者30人，男12人，女生18人，平均年龄21.4岁。所有被试者均无生理和心理方面的既往病史，裸眼视力或矫正视力达1.0以上，色觉正常，均为右利手。

2.3 试验设备及测评量表

试验主设备为搭载15英寸显示屏的戴尔笔记本电脑，安装ErgoLAB3.0试验平台，连接Tobii Pro X2-30眼动仪 (采样率30Hz)，试验任务通过E-Prime 2.0软件编程实现。

2.4 试验程序

提前与需要参加试验的被试者约定时间，提醒被试者参加试验之前充分休息。正式试验之前，让被试者保持舒适坐姿，调整被试者视距，确保眼动仪正常捕捉被试者的眼动数据。为被试者讲解试验规则和注意事项，被试者充分理解后正式开始试验。打开ErgoLAB3.0录屏功能，同时运行E-Prime程序，被试者完成9个Trial测试任务。执行完毕后停止E-prime程序，关闭ErgoLAB录屏。

2.5 数据采集与整理

试验过程中，E-prime程序自动采集绩效数据CRT，Tobii眼动仪采集被试者眼动数据SR、FT、PD，ErgoLAB平台保存眼动数据。运用SPSS软件，按D1、D2、D3水平将CRT、SR、FT、PD (左、右瞳孔直径均值) 指标数据进行分类整理，剔除错误反应数据后，分别获取D1、D2、D3水平下指标数据87、86、79组。

3 基于HMM的认知性VDT监控作业过程识别

实验过程中，所有被试者在D1、D2、D33个水平的正确反应trial数分别为87、86、79，合计252组。对3水平的CRT进行差异分析，方差分析结果见表2。

表2 方差分析结果Table 2 Results of varionce analysis

结果显示，在不同难度水平下作业绩效存在极显著差异 (P=0.005＜0.05)。分别对D1、D2、D3水平的作业过程进行识别，后文以D1水平为例阐述研究过程。

3.1 确定观察集合及观察序列

3.1.1 生理观察数据离散化

D1水平下共有30名被试者正确完成了87个trial的测试任务。Tobii Pro X2-30眼动仪采集了每次测试过程的眼动数据，该设备的采样频率为30 Hz，每个trial的采样时刻总量为30×C RT/1 000，将每个采样时刻记为hi。PD为时刻数据，以hi时刻的左右瞳孔直径均值对该时刻的PD赋值。SR、FT为时段数据，按30 Hz的采用频率，将SR、FT转化为时刻数据。具体转化方式如下。SR：在有眼跳的时段hi-1～hi，以hi-1时刻视点像素位置与hi时刻视点像素位置的距离对hi时刻SR赋值，没有眼跳的时段hi-1～hi，hi时刻赋值0；FT：在有注视的时段hi-1～hi，hi时刻赋值33 ms (设备采样率为30 Hz，1 000 ms/30=33 ms)，没有注视的时段hi-1～hi，hi时刻赋值0。由此，每个trial的眼动观察数据可以离散化为3×x的矩阵观察数据，x由该trial的采样时刻总量决定。D1水平下共产生87组3×x的矩阵观察数据。由于篇幅原因，仅给出第1个trial的矩阵观察数据 (3×84)，见表3。

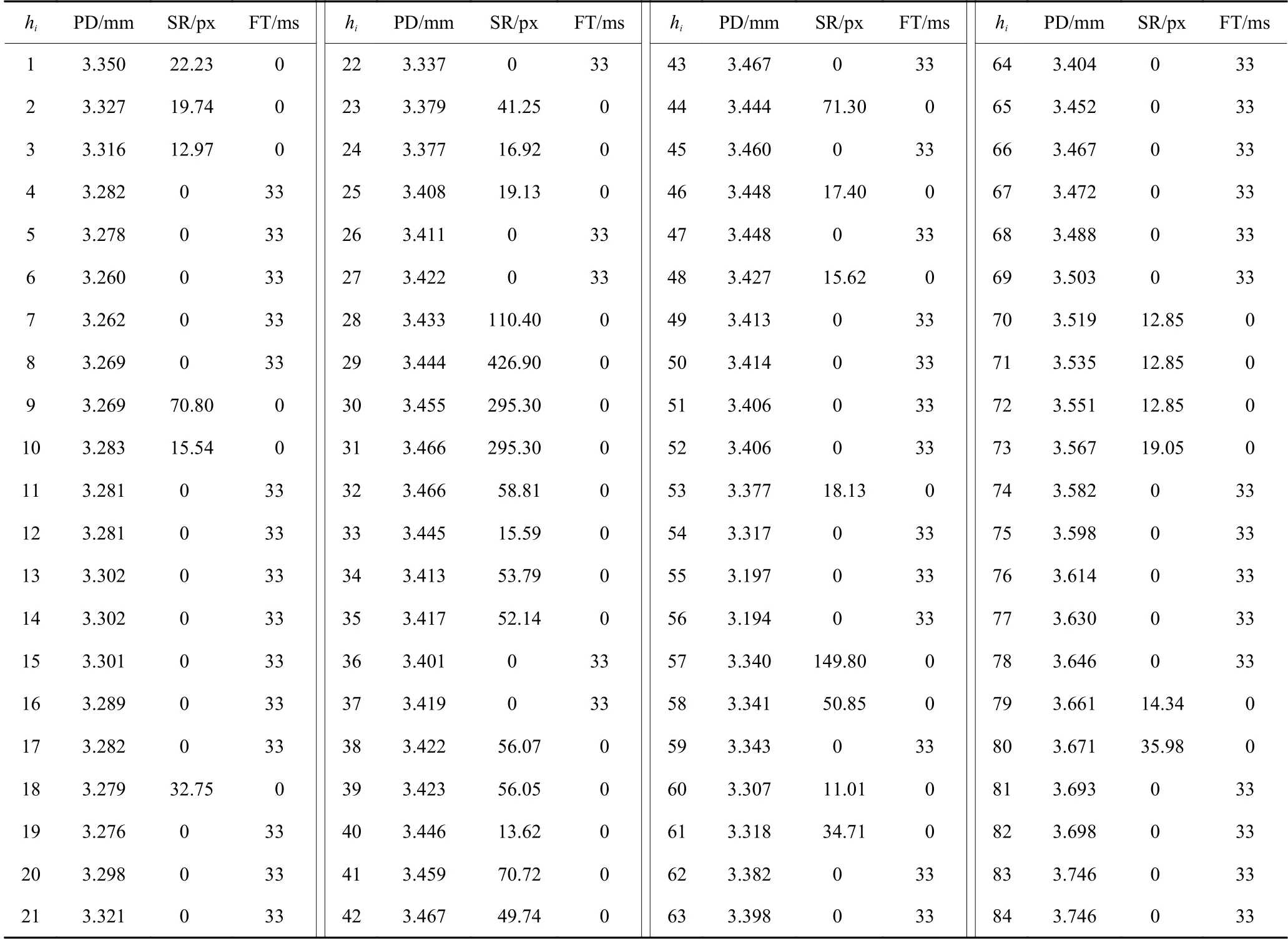
表3 第1组观测数据Table 3 Observation data of the first trial

3.1.2 基于多维有序聚类和K-Means聚类提炼观察集合

HMM的观察集合通常从一定数量的观察序列中提炼生成，但眼动特征观察数据的时序密度过高，无法用常规方法提炼观察集合。观察数据为时序数据，分类必须满足相邻条件，按照类内离差平方和最小、类间离差平方和最大的原则，采用文献[20]提出的多维有序聚类方法，运行Matlab 2013a分别对87组原始矩阵观察序列数据进行多维有序聚类，得初步观察序列i=1,2,···,87。由于篇幅原因，仅给出第1组结果，见图3。

图3 8层分割聚类Figure 3 Eight-layer segmentation clustering

从图3可知，第1组观察数据按时序分为8类为最优分割，可得初步观察序列共8个观察项，每个观察项由3项眼动特征信息序列构成。87个初步观察序列的所有观察项之和为902(略)，对902个观察项进行K-Means聚类分析，结果见表4。

表4 K-Means聚类结果Table 4 Resultsof K-Means clustering

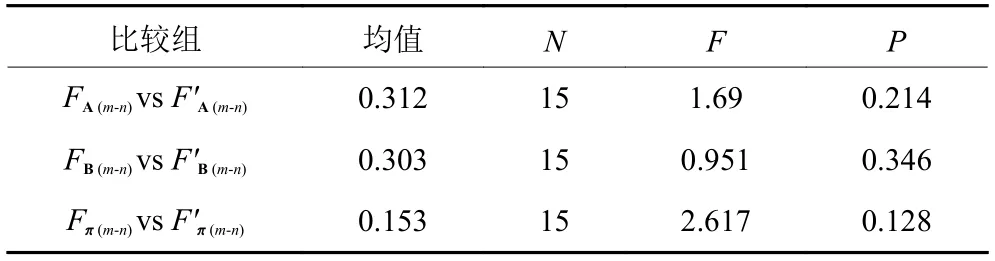
表5 F范数t检验结果Table 5 t text results of F norms

由表4可知，当聚类数为12时，轮廓系数最大。因此，将902个观察项分为12类 (c1,c2,···,c12)，即为认知性VDT监控作业 (D1水平) 隐马尔可夫过程观察集合的基本构成要素。由此，观察集合V={v1,v2,···,v12}，v1=c1,v2=c2,···,v12=c12。

3.1.3 确定最终观察序列

同理，可分别求解D2、D3水平的86、79个最终观察序列。

1.2.2 抗胃癌植物类中药 以“中药”“抗肿瘤”等为检索词，在中国知网、维普等数据库中组合查询1980年1月－2018年4月发表的相关文献。纳入抗胃癌植物类中药的相关文献，包括基础/临床研究、综述、个案报道等；排除不在“1.2.1”项下所列品种范围内的相关文献。共检索到抗胃癌植物类中药相关文献478篇，共涉及85个中药品种。

3.2 HMM参数训练及验证

3.2.1 参数训练

BW (Baum-Welch) 算法是确定隐马尔可夫模型参数 λ=[A,B,π]常用的无监督学习方法，由于该方法仅使用1个观察序列训练，因而不存在一个最佳方法来估计模型参数。本研究采用多观察序列无监督算法[21]训练模型参数。传统机器学习对训练样本比例没有特定的要求，一般设置为30%或20%，具体视总样本量的大小而定，总样本量较小则训练样本比例较高。本研究D1水平下总观测序列样本量为87，数量较小，将30%的观察序列用于HMM参数训练[21]。随机选择26 (87×30%) 个观测序列，重新排序构成训练观察序列集合O=[O(k)]=[O(1),O(1),···,O(26)]。基于文献[21]的方法，通过Matlab 2013a编程实现算法。输入训练观察序列集合O和初始参数λ0=[A0,B0,π0]，初始参数采用均匀赋值方法[12]，设置迭代次数5 000，精度0.000 1。训练得到D1水平HMM参数λ 优化后的结果

同理，可分别求解D2、D3水平HMM参数 λ优化的结果。

3.2.2 参数可信性验证

3.3 作业过程识别

Viterbi算法是HMM解码问题最常用的方法。该算法采用动态规划求解最优状态序列 (概率最大路径)，每条路径对应从初始到终止时刻的状态序列Q=[q1,q2,···,qT]。从t=1开始，推算下一时刻以各状态节点为终点的所有可能状态序列的概率并确定最优状态序列，直至t=T[12]。具体步骤如下。

首先定义 δt(i)表 示时刻t状态为i的最优局部状态序列的概率，ψt(i)表 示该状态序列的t-1个节点。此处以及后面的式 (4)～ (10)，i表示状态序列[q1,q2,···,qT]中的时刻t的状态q，值为si，i=1,2,···,13。如i=2，表示时刻t的状态为s2。

1) 按照式 (4) 设定初始化条件。

式中，δ1(i)表 示在时刻1状态为i的最优局部状态序列的概率；ψ1(i)表示状态序列的第0个节点。

3) 通过递推，计算最优状态序列。

式中，Pr∗表示最优总概率。

式中，I∗表示最优状态序列。

从表6可以看出，状态序列反映被试者的认知过程。在同一难度水平下，不同被试者的状态序列也存在差异；不同难度水平的状态序列差异更大，随着难度水平的增加，状态序列的长度随之增加。

表6 状态序列结果Table 6 Results of state sequences

4 绩效形成机理分析

1) 认知动素链长度对绩效的影响。

根据试验数据，对表6中6种认知动素链的CRT均值进行差异比较，方差分析结果见表7。结果显示，6种认知动素链的CRT均值差异显著 (P=0.034＜0.05)。

表7 方差分析结果Table 7 Results of variance analysis

根据表6中6种认知动素链对应的90组样本数据，对认知动素数和CRT进行相关性分析，结果如表8所示。可以发现，认知动素数与CRT之间存在显著的正相关性，认知性VDT监控作业的绩效随着作业过程中认知动素数量的增加 (即认知动素链长度的增加) 而降低。从试验设计及结果分析，导致认知动素链长度增加的主要原因如下。(1) 由任务信息提示界面与任务操作界面之间的时距过长所致的任务难度增加；(2) 被试者个体因素：本文试验数据中，不同被试者在同一难度水平下认知动素链长度存在差异的情况较多。但被试者特征 (比如，人格特征) 与认知动素链结构之间的关系还有待进一步研究。

表8 相关分析结果Table 8 Results of correlation analysis

2) 认知动素链构成要素及结构。

随着认知动素链的增长，构成要素之间的结构会变得愈加复杂。表6显示，D3水平两种认知动素链的动素数量均为13，但是绩效存在差异。这表明构成要素的类型及构成要素之间的结构差异亦会影响绩效，但是何种结构会产生更好的绩效，以及如何通过培训和任务界面设计来重构和优化作业者的认知动素链还有待进一步研究。

5 结论

本文针对认知性VDT监控作业过程的内隐性，运用E-prime设计实验任务，运行ErgoLAB实验平台采集作业绩效及眼动数据，运用隐马尔可夫模型解析作业过程并分析绩效形成机理。结果表明，认知性VDT监控作业过程可以用认知动素链表征，作业者和任务的不同会导致认知动素链的差异；在结构相同的条件下，认知动素链越长，认知性VDT监控作业绩效越差；在长度相同情况下，认知动素链的构成要素和结构差异会影响认知性VDT监控作业绩效。

本文为其他作业类型的分析和研究提供了可借鉴的范式和思路，但目前的研究还仅限于认知性VDT监控作业，作业者个体因素对认知动素链的影响规律，以及如何通过人员培训和任务优化设计来重构和改进作业者的认知动素链等问题还有待进一步研究。