客货邮融合下城乡客运车辆调度双层优化方法
鲁芳,黄彬,闫蕾朵
(1.中南林业科技大学 物流与交通学院,湖南 长沙 410004;2.湘潭大学 商学院,湖南 湘潭 411105)
公共交通是农村地区服务乘客出行需求的重要渠道。面对农村地区长期以来乘车难、出行不便、物流基础设施配套不完善等问题,各地相继推出客货邮融合发展方案,通过整合交通运输和邮政双方资源,充分利用公交 (客运) 车辆并解决快递配送问题。客货邮融合是以资源共享、客货兼顾、运邮结合、融合发展为原则,利用遍布城乡的农村客运网络资源以及客运班车的富余装载空间,积极推进农村客运、货运、邮政快递融合发展,解决农民群众出行、物流配送、邮政寄递3个“最后一公里”问题,实现客货邮多赢[1]。但由于农村地区乘客需求少且居住区域分散,因此农村地区客运车辆存在着发车间隔长、发车频次少等情况,同时部分农村区域公共交通需要进行车辆换乘以抵达目的地,使得客货邮融合在实施过程中面临着客运车辆营运成本高、货件配送时间长等问题。
通过考虑客货邮融合下的车辆调度问题,研究乘客与货件共同在农村客运线路之间进行换乘,既可以实现车队规模优化,减少客运企业的运营成本,又可以减少乘客与货件的旅行时间,从而解决客货邮融合实施过程中面临的营运成本及货件配送时效性问题。车辆调度的研究热点是对时刻表进行优化。沈国江等[2]针对现有公交系统中公交在时间和空间上分布不合理的情况,通过运用非等间隔发车的方式来设计公交时刻表。Guo等[3]通过使用混合整数规划方法,设置轨道交通末班车发车、运行、停留及到站时间,实现城市轨道交通网络的运行效率优化。刘志刚等[4]运用协同发车方法,以最大限度减少乘客换乘时间为目标编制公交时刻表。Fouilhoux等[5]考虑高峰期和平峰期下不同发车间隔的情况,以实现协同次数最大为目标建立时刻表模型。Ceder等[6]结合均匀发车间隔和均匀载重两种概念,对多种车型的车辆时刻表进行编制。
上述研究仅单纯考虑车辆时刻表优化问题,而在关于车辆调度的研究上,许多学者从对单一的时刻表优化模型进行研究,逐步转到对综合考虑乘客需求分布、车辆到站次数以及车队规模等因素的多目标模型研究之中。杨信丰等[7]建立多目标公交同步换乘协同调度优化模型,在考虑车辆平均满载程度的背景下,实现同步换乘人数最大以及乘客总等待时间最少。魏明等[8]以不同类型出行者等待时间最少和各类车辆到达站点时的泊位数最多为目标,综合考虑乘客在不同交通方式之间的换乘。慈玉生等[9]以实现区域公交行车计划编制优化为目标构建双层规划模型,并结合3类核算时间点来对车队规模进行约束。Liu等[10]在考虑用户需求分配的背景下,提出一种采用逆差函数方法的双目标双层模型,分析行程变化对公共交通用户路径选择行为的影响。Mirabi[11]采用混合电磁算法,对以车辆总行驶距离和客户总等待时间为目标的双目标模型进行求解,实现车辆调度优化。Wu等[12]考虑换乘乘客总数、优化后时刻表与现有时刻表的最大偏差,构建多目标优化模型设计时刻表以实现同步换乘。
从以上的文献中可以发现,车辆调度的研究主要集中于城市公共交通背景下的乘客换乘。由于农村交通基础设施在道路数量、通达度方面与城市存在着差距,使得考虑城市交通背景下的换乘方式选择、乘客需求分布等车辆调度研究并不适用于农村区域,因而对农村地区乘客换乘的研究也引起学者关注。Takamatsu等[13]结合日本农村地区现有交通情况,将实现农村地区乘客双向联系换乘列入考虑,通过混合整数规划模型设计时刻表缩短乘客在公交与火车间换乘的等待时间。胡宝雨等[14]在研究城区内部和城区边缘两种同步换乘形式的基础上,结合农村客运换乘枢纽的功能和布局,考虑乘客对换乘路径的选择,构建一种包含乘客换乘时间、车辆在有效换乘站相遇次数的双层规划模型。Petersen[15]利用以脉冲时间表为基础的网络规划方法,针对人口密度低的农村地区,通过调整脉冲网络的运作间隔,实现乘客在不同交通服务间的换乘并改善车辆占用情况。
虽然以上国内外学者针对车辆调度问题进行了富有成效的研究,并基于农村地区换乘枢纽布局、人口密度等实际情况对车辆调度进行探讨,但是结合客货邮融合将客货共同运输和车队规模进行综合考虑的研究还比较匮乏。因此,本文考虑农村地区乘客出行与货件配送问题,将“城乡客运+货件”的客货邮融合共享运营模式与车辆调度进行结合,构建一个双层规划的双目标模型来实现农村区域车辆调度优化,以实现客货总旅行时间和车队规模最小化,从而解决客货邮融合过程中面临的货件配送时效性及营运成本问题,为实现客货邮融合下的车辆调度优化提供理论支撑与指导意义。
1 考虑客货邮融合的城乡客运车辆调度问题
区域内车辆网络系统由换乘站和城乡客运车辆途径的各站点组成。城乡公交从县城始发站点s出发后,可将前往镇村的下行乘客P和货件E运输至镇级换乘站,再由经过该换乘站的班车将乘客与货件运输至周边村级站点和服务网点,需上行前往县城的乘客与货件也可经公交和班车线路到达县城。客货邮融合下运营模式如图1所示。通过城乡客运车辆能够满足乘客与货件的运输需求,并将乘客与货件送达相关的站点。车辆调度与车队规模密切相关,考虑到客货邮融合模式下农村区域存在多条镇村班车线路,因而通过考虑班车车队规模可以帮助企业降低运营成本。

图1 客货邮融合下运营模式Figure 1 The operation mode under the integration of passenger,cargo and express mail service
根据公交线路与班车线路的布局关系,可将区域内线路分为连接城市与镇的公交线路以及连接镇村间的班车线路。公交线路负责城市与换乘站间的乘客运输,班车线路负责不同镇村之间的乘客运输。将公交线路与班车线路作为一个整体进行车辆调度研究,研究换乘乘客的旅行时间,并使用客运车辆进行货件配送和收货,此时车辆调度问题是关于客货邮融合下城乡客运车辆的调度优化。
本研究中目标函数分为乘客与货件总旅行时间Z1和车队规模Z2。Z1越小,表明客货邮融合减少乘客与货件运输与换乘时间的效果越显著;Z2越小,客运车辆运营企业在运营过程中所需使用车辆数量越少,表明通过车辆调度可以降低企业营运成本。模型构建过程中所用到的基础参数如表1所示。

表1 参数定义Table 1 Parameter definitions
模型建立时考虑以下假设:
1) 对任意线路,车辆在站点间的行程时间受随机事件的影响忽略不计;
2) 货件在县级始发站按镇级单位进行分拣,在各站点只考虑货件的装卸时间;
3) 车辆的载客载货能力足够大,不存在需在站点进行换乘的乘客和货件的滞留情况;
4) 车辆在沿线各站点停靠时间较短,忽略停靠时间;
5) 乘客与货件在到达换乘站后选择乘坐最近一趟可换乘的车次离开。
2 城乡客运车辆调度双层优化模型
2.1 以总旅行时间最少为目标的上层模型
总旅行时间由乘客与货件两部分组成。乘客旅行时间一般包括乘客乘车时间和换乘等待时间。客货邮融合下,货件随乘客共同运输,因而对货件在各站点的装卸时间进行考虑。
1) 乘客乘车时间总和PH为
2) 乘客换乘时间总和。假定到达换乘站的同一组乘客具有相同的换乘步行时间和上下车时间,在车辆容量足够的情况下,该组乘客只需一次就可以实现换乘衔接,则换乘等待时间可表示为
3) 货件装卸时间总和。在客货邮融合下,乘客与货件在到达换乘站后共同等待可换乘车次,因而可以只计算乘客换乘等待时间,对货件而言只需对其在r路线上的不同站点的装卸时间fj和在公交始发站进行装卸所产生的时间fs进行计算,货件总装卸时间ET具体计算见式(5)。
此外,为了检验客货邮融合的效果,本文考虑货件运输时间以计算客货分离下的总旅行时间。
4) 货件运输时间总和EH具体计算见式(6)。
根据上述分析,构建考虑乘客与货件总旅行时间的上层目标函数如式(7)所示。
2.2 以车队规模最少为目标的下层模型
下层模型的目标是尽量减少所需的车辆数量,这是从车辆运营企业的角度来考虑。因此本文构建以车队规模最小为目标的函数Z2,目标函数的表达式见式(8)。
车队规模受发车间隔方案的影响,为了求解模型,本文将下层目标函数Z2转化为目标函数Z1的约束条件,通过构建约束条件使得模型从双目标模型转化为单目标模型,相关约束条件的构建如下。
1) 车队规模由发车间隔方案所确定的时刻表得出。本文研究农村区域乘客与货件换乘,对公交与班车两种类型车辆的发车间隔方案进行约束,发车间隔方案与发车次数相关,因此通过对发车次数方案进行约束以实现对发车间隔方案的约束。
设区域内有公交线路a,存在n种发车次数方案,n=La,La+1,La+2,...,Ua-1,Ua。La和Ua分别表示路线a上车辆出发次数的上下限。决策变量表示在发车间隔固定的情况下,一种公交发车方案是否被选择,决策变量表示为
同样地,对于班车线路r上的车辆,存在m种发车次数方案,m=Lr,Lr+1,Lr+2,...,Ur-1,Ur。Lr和Ur分别表示路线r上车辆出发次数的上下限。决策变量表示在发车间隔固定的情况下,一种班车发车方案是否被选择,决策变量表示为
2) 在定义有关发车方案的决策变量后,需对发车方案进行约束。通过为公交与班车分别确定一种发车方案,从而确定一组固定的时刻表以计算换乘时间。本文分别构建关于公交与班车的两组约束条件,保证对于公交与班车在给定的路径下分别只能选择一种发车方案,因此对车辆出发次数约束表示为式 (11)~ (12)。
3) 客货邮融合模式下,镇村班车存在多条班车线路,因此本文结合发车方案所确定的班车时刻表,对班车车队规模进行约束。首先需要对各个站点所使用的车辆数量进行约束,各站点班车逆差函数边界的约束表示为
其中,d(j,t)是 由所选择发车次数方案决定的,其表示在时刻t前站点j的车辆出发次数减去到达次数的净额;[H1,H2]为车辆调度的时间范围;D(j)表示在车辆调度范围[H1,H2] 内d(j,t)的最大值,即发车次数方案所确定的时刻表下车站j需要的车辆数量。
在对各站点使用车辆进行约束的基础上,对班车车队规模进行约束。所有站点需用车辆的数量不应超过最小车队规模N0,N0可由逆差函数法求得。因此,关于班车车队规模的约束条件表示为
通过上述约束,可以将目标函数车队规模Z2转换为目标函数Z1的约束条件。
3 基于逆差函数的城乡客运车辆调度求解算法
所构建的模型属于多目标优化问题,为了降低模型求解难度,本文参考文献[10],采用一种基于逆差函数的车队规模搜寻方法来确定可选的车队规模,将原来的双目标规划模型分解为单目标规划模型,从而显著降低问题的复杂性。本文研究的是农村地区车辆调度问题,根据不同发车间隔方案所确定的时刻表,利用逆差函数计算出班车车队规模的上下限并构建约束条件。
逆差函数是一种阶跃函数,这体现在它的变化都是以1为步长进行调整,若对应的车站有车辆发出时,逆差函数相应增加1;若有车辆到达车站时,函数值相应减小1。因此,在研究车辆调度问题时,逆差函数可以表示在研究区域内,任意线路在任意时刻下的任一场站的车辆占用情况。如果对于一组固定行程,所有行程的开始和结束都在调度范围[H1,H2]内且没有空驶车次插入,则所有行程所需的最小车辆数N0等于总逆差函数D(j)之和,同时等于所有站点j的最大逆差值d(j,t)之和。
依据以上分析,基于逆差函数的客货邮融合下车辆调度问题算法如下。
步骤3解决方案输出。对不同车队规模w下对应的目标函数值Z1进行计算。生成相关目标函数值(Z1,Z2),从而生成帕累托有效解决方案。
4 数值分析
在本节中,通过设定示例网络 (见图2) 进行时刻优化,以检验所提出的模型和基于逆差函数的求解方法在双目标问题中的应用。本文仅考虑一条班车线路的换乘情况。如图2所示,示例网络由1个公交站点 (0)、1条公交线路 (a1)、1条班车线路 (r1)、1个换乘站点 (1) 以及班车沿线站点 (2、3、4) 组成,调度模拟窗口为7:00~ 12:30。图2中各站点间的数字表示客运车辆在站点间的平均旅行时间(min)。表2为各路段运行数据,表3和表4分别为给定时期内的下行和上行乘客和货件数量。另外,本文设定乘客与货件在换乘站换乘步行平均时间War为0.5 min,上下车所需的平均时间g设为0.5 min。同时设定货件在各个站点的平均装卸时间为3 min。

表2 各路段运行数据Table 2 Operation data of each road section

表3 换乘乘客及货件数量 (下行)Table 3 Number of transfer passengers and cargoes (downstream)

图2 示例网络Figure 2 An example of networks
由于农村地区道路设施等条件限制,使得公交线路与班车线路在发车间隔上存在着差异,导致两者在发车时刻表和发车次数上有着区别。表5和表6为城乡公交线路a1运行情况,x1、x2分别表示公交线路在发车次数q=7和q=6时的发车方案。本文研究班车路线r1上下行方向各有两种发车次数 (q=3和q=4) 的情况,并对上下行方向的不同发车次数进行变量定义,即x3、x5分别表示班车在发车次数q=3时下行和上行的发车方案;x4、x6分别表示班车在发车次数q=4时下行和上行的发车方案,如表7和表8所示。

表5 路线 a1终端节点的出发和到达时间 (下行)Table 5 Departure and arrival times of terminal nodes of route a1 (downstream)
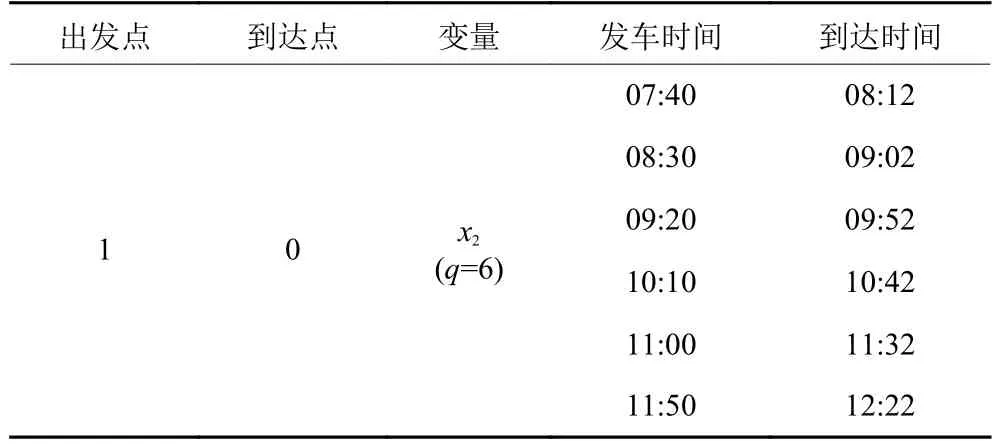
表6 路线 a1终端节点的出发和到达时间 (上行)Table 6 Departure and arrival times of terminal nodes of route a1 (upstream)
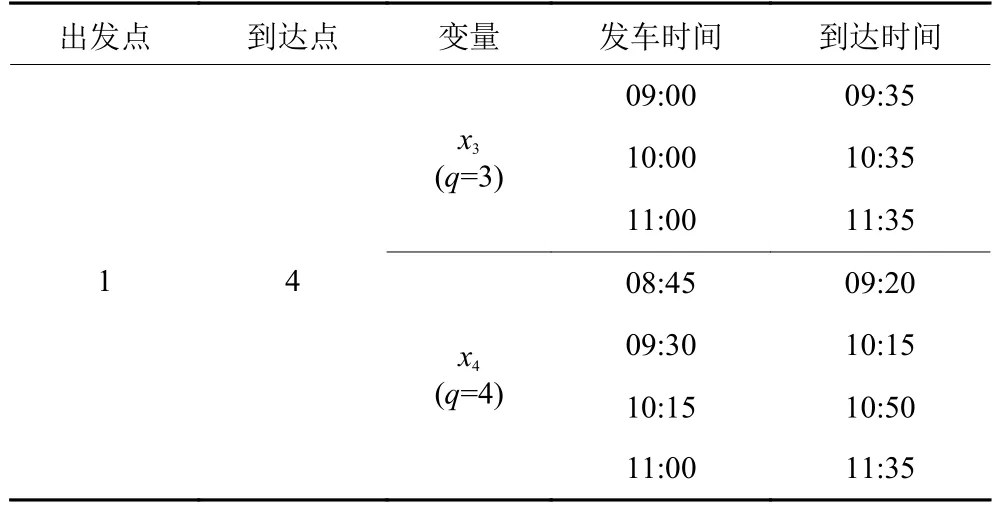
表7 路线 r1终端节点的出发和到达时间 (下行)Table 7 Departure and arrival times of the terminal nodes of route r1 (downstream)
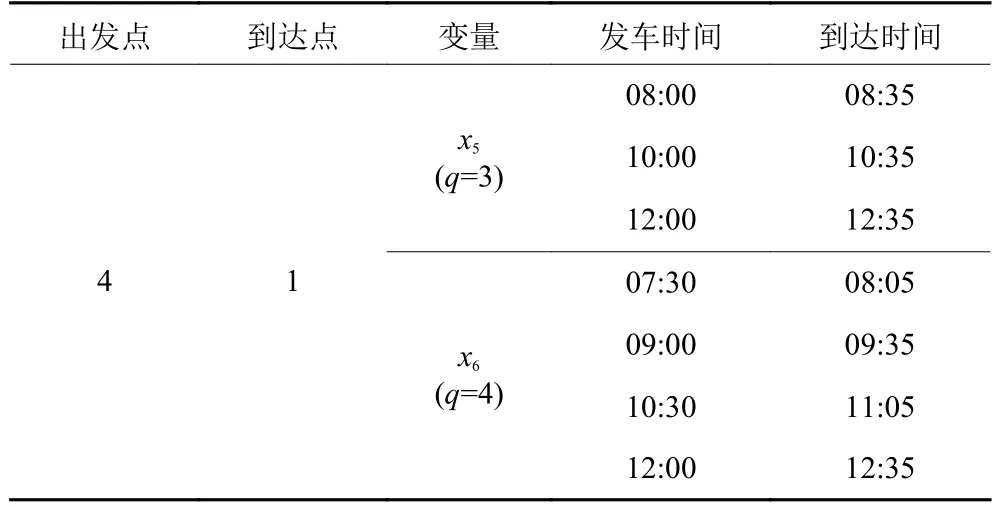
表8 路线 r1终端节点的出发和到达时间 (上行)Table 8 Departure and arrival times of the terminal nodes of route r1 (upstream)
应用逆差函数估计方法,可以得到示例中班车时刻表情况下的车队规模,如图3、图4所示。通过图3和图4所示的逆差函数得到车队规模的下界和上界。其中,d(1,t)和d(4,t)分别表示线路r的第1个和第4个车站,在时刻t下的逆差函数的值,即在时刻t前站点1和4的车辆出发次数减去到达次数的净额;D(1)和D(4)则分别指在时刻表范围[7 :00,12:30]上d(1,t) 和d(4,t)最大值,表示在时刻表控制下各个车站所需要车辆的数量。图3基于班车最小出发数,即(x3,x5),得出车队规模下界NL=D(1)+D(4)=2;图4基于班车最大出发数,即(x4,x6),得到车队规模上限NU=D(1)+D(4)=4。在计算车队规模下界和上界的基础上,可以将原双目标非线性整数规划问题分解为2个目标函数已知的单目标整数规划问题 (Z2=N0=2,4),随后基于求得的车队规模值,构建有关班车车队规模的约束条件。
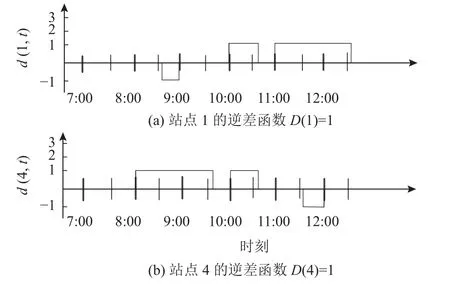
图3 利用逆差函数估计示例时刻表的车队规模下限Figure 3 The lower limit of the fleet size evaluated by the deficit function with an example schedule
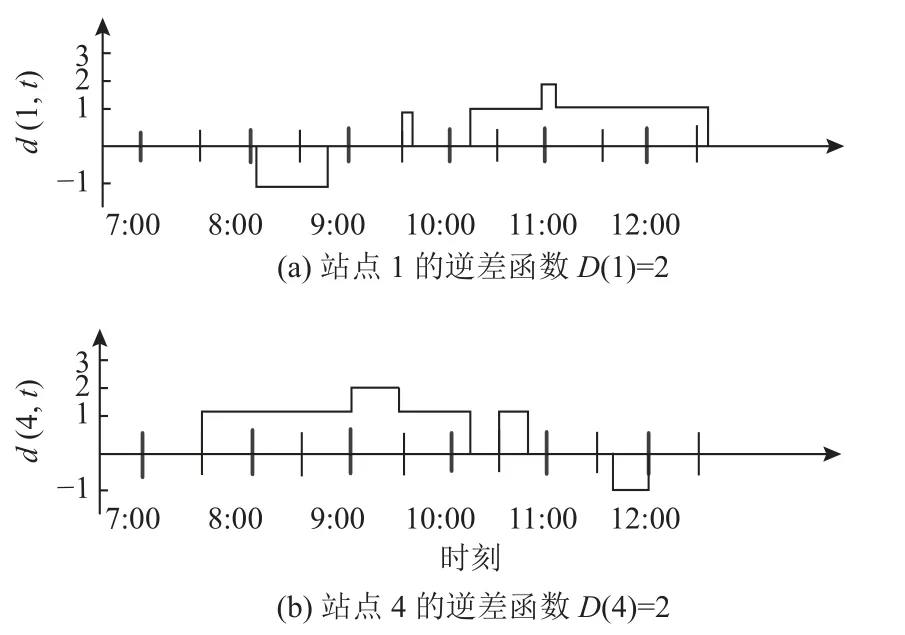
图4 利用逆差函数估计示例时刻表的车队规模上限Figure 4 The upper limit of the fleet size evaluated by the deficit function with an example schedule
在客货邮融合下,货件按照班车时刻表与乘客共同进行换乘和运输,因而总旅行时间主要包含上下行方向乘客的乘车时间、换乘时间及货件装卸时间。由此对得到的两个单目标整数规划问题进行求解,得到以下两组Pareto有效解。
上述解集是客货邮融合下乘客与货件的总旅行时间。为了检验农村地区实行班车客货共同运输的有效性,本文考虑计算乘客与货件分开进行换乘与运输的情况。客货分离下,乘客仍按照现有时刻表在换乘站进行换乘,而货件将由快递公司单独进行配送和揽收,因而总旅行时间包含乘客乘车时间、换乘时间、货件运输时间及装卸时间。本文假定快递公司配送路线与示例网络相同,换乘乘客与配送货件数量不变,客货邮融合与客货分离两种运输情况下总旅行时间解集比较如图5所示。

图5 总旅行时间解集比较Figure 5 Comparison of total travel time solution sets
此外,在农村区域客运车辆中,公交发车次数和车辆数明显多于班车。在均匀发车的情况下,公交各车次发车时刻约束直接影响时刻表的优化效果,因此分析该参数变化对时刻表优化效果的影响,可以进一步优化基于逆差函数的求解方法所得到的结果,并为公交运营企业选择线路的发车时刻提供依据。考虑到农村区域城乡公交和班车发车间隔时间较长,当时刻的调整取值较小时,优化效果并不明显,因此本文对公交发车时间约束在原时刻表基础上分别提前和延后3、6、9、12 min。对不同时刻调整取值下目标函数Z1的优化效果进行分析 (见图6),图6中的时间0表示现有时刻表的发车时刻,-3、-6、-9、-12与3、6、9、12表示与现有时刻表的发车时刻相比,车辆最早发车时刻以及此后各车次的发车时间分别提前和延后3、6、9、12 min。
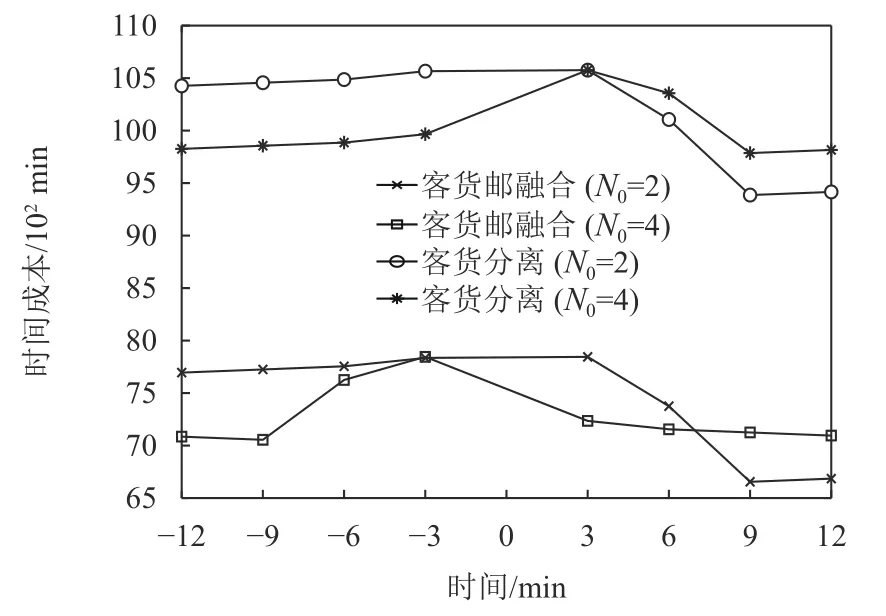
图6 不同发车时刻调整下的总旅行时间对比Figure 6 Comparison of total travel time with different departure times
通过图5可以发现,客货邮融合下,车队规模为2时,相应的目标函数Z1计算值为7 815 min,相较于客货分离下的目标函数值10 546 min,乘客与货件总旅行时间减少幅度为25.89%;车队规模为4时,相应目标函数Z1计算值为7 215 min,相较于客货分离下的目标函数值9 946 min,乘客与货件总旅行时间减少幅度为27.46%。以上对比结果验证了客货邮融合模式的有效性。同时通过对图6不同发车时刻调整下的总旅行时间进行分析,发现对车辆发车时刻进行调整,也能优化不同车队规模下乘客与货件的总旅行时间。在本算法计算结果的基础上,班车运营企业可以在乘客与货件时间成本和车队规模之间进行权衡,根据自己的期望和实际考虑对运营方案进行调整,而且还可以为车辆的发车时刻的修正提供决策支持。
5 结论与展望
本文结合客货邮融合,考虑乘客与货件的共同运输,通过构建考虑客货邮融合的车辆调度双层规划模型,解决客货邮融合实施过程中面临的客运车辆运营成本高、货件配送时间长等问题。此外,为了降低模型求解难度,本文在模型中利用逆差函数原理构建了车队规模约束条件,将原本的双层模型转化为单层模型,对客货邮融合下的模型进行求解。通过算例分析对模型的有效性进行检验,结果表明,将客货邮融合与车辆调度进行综合考虑的策略可以有效减少不同车队规模下乘客与货件的总旅行时间,在提升农村地区客运服务质量的同时解决农村地区货件配送与揽收问题,而通过调整公交发车时刻则可以进一步提升客货邮融合的车辆调度有效性。但当前研究仍存在进一步提升空间,考虑到农村地区情况的复杂性,在后续研究中有必要对多条换乘线路、不同乘客与货件需求等情况进行深入研究。

