基于改进NSGA-II的铁路项目进度计划多目标优化

周国华，马依婷

(西南交通大学 经济管理学院，四川 成都 610031)

近年来，为深入贯彻党的十九大作出的建设交通强国重大决策部署，我国铁路路网规模持续扩大，投资力度不断增强[1]。面对如此大规模、高投资的铁路建设项目，科学高效的项目管理是保障铁路建设工程高质量发展的关键。因此，研究铁路项目的工期费用优化问题至关重要。

因项目中各活动不断重复进行，铁路项目在建设工程领域被称为重复性项目。现有研究指出传统计划方法对于重复性项目的不适用性，并提出了针对重复性项目设计的调度方法和技术。其中，最具代表性的是重复性调度法(repetitive scheduling method，RSM)[2]。RSM方法利用二维坐标呈现出项目的时间进度和空间进度，能够较好地满足重复性项目对资源连续性的要求，具有更强的生动性、可读性，对铁路项目具有独特的适用性[3]。

重复性项目时间费用权衡问题 (time-cost tradeoff problem with repetitive projects,TCTPRP) 是一类离散时间费用权衡问题 (discrete time-cost tradeoff problem,DTCTP)，属于NP难问题[4]。因此，目前大多数研究已应用诸如遗传算法等智能算法来解决TCTPRP问题。Hyari等[5]依据Pareto原理提出能够同时最小化工期和费用的遗传算法；Long等[6]把费用和工期整合到一个目标函数，设计遗传算法求解；相似地，王伟鑫等[7]以效用函数将工期费用整合为一个目标函数，设计满足软逻辑关系约束的云遗传算法；张立辉[8]和Huang等[9]提出采用三段式整数编码和双层交叉算子的遗传算法，通过horizon-varying方法得到了Pareto曲线；Shahriari等[10]和Heravi等[11]使用多目标算法同时对工期和费用进行优化。

相较一般重复性项目，铁路项目施工里程较长，涉及到的活动类型更复杂，往往存在逆向施工线性活动 (如架梁)、条状活动 (如深水桥梁基础、桥塔)、块状活动 (如长大隧道) 等特殊活动。因此，考虑多种活动类型，拓展施工场景，能够提高模型对于铁路项目的适用性。然而，目前几乎所有TCTPRP研究均将研究对象聚焦于正向施工线性活动。刘仍奎等[3]虽然在模型中考虑条状活动和逆向施工线性活动，但是未考虑与项目不同方面相关的若干成本要素，并且缺少可行的智能算法进行求解，无法实现大规模铁路项目优化。

综上所述，本文的主要研究贡献体现在以下两点。1) 在模型方面，现有研究仅考虑了正向施工线性活动，施工场景单一，虽然简化了求解过程，但是降低了模型对铁路项目的适用性。针对铁路项目施工计划优化在施工场景及约束表达等方面存在的欠缺，本文基于RSM完善铁路施工计划方法的数学表达和约束体系，在传统重复性项目时间费用优化问题的基础上增加对于条状活动、块状活动、逆向施工线性活动的优化，以总工期最短和总费用最低为目标建立考虑多模式的多目标优化模型。2) 在算法方面，现有文献尚未针对包含特殊活动的大规模铁路项目提出智能优化算法，为填补这一空缺，本文提出适用于铁路项目的改进NSGA-II算法。首先，针对铁路项目特征设计活动调度流程；然后，为提高算法寻优能力，设计均匀进化的精英选择策略，并引入差分进化算法的变异、交叉算子，构造出分层多策略自适应的变异、交叉算子；最后，用一个算例验证模型的合理性和算法的有效性，并通过与传统NSGA-II对比，证明改进后的算法性能更加优越稳定。

1 问题描述

一个铁路项目中有I个活动J个单元。各活动在施工范围内具有重复性特征，即相同活动在不同施工单元内重复进行。基于RSM框架，项目中包含线性、块状和条状活动。线性活动在施工范围内连续施工 (如无砟道床、架梁)；条状活动在一个固定里程点进行施工 (如深水桥梁基础、桥塔)；块状活动在一段固定区间内进行施工 (如长大隧道、特殊结构桥梁)。其中，线性活动可逆向施工或正向施工，逆向施工指从项目终点方向向起点方向施工，反之，即为正向施工。

本问题包含以下关键决策：1) 线性活动施工方向；2) 各活动各单元施工模式；3) 各活动开工时间和结束时间。

1.1 基本假设

1) 活动间优先关系为“开始-开始”型、“结束-结束”型、“结束-开始”型和“开始-结束”型；

2) 线性活动在各单元间连续施工，且在全施工段落内仅能选择一个施工方向;

3) 各活动施工模式可选，在同一单元内只能选择一种施工模式。

1.2 符号定义

本文符号定义如表1所示。

表1 符号定义Table 1 Symbol definitions

决策变量定义如下。

2 数学模型

2.1 目标函数

1) 项目总工期最短。

项目总工期D为第1个活动开始时间到最后1个活动结束时间，目标函数如下。

2) 项目总费用最低。

项目总费用由直接费用 DC和 间接费用 IC组成，其中直接费用包括人工费用、材料费用和设备费用，间接费用为间接费用率和工期的乘积。目标函数如下。

2.2 约束分析

由于模型考虑了逆向施工线性活动、条状活动和块状活动，因此各个活动之间的时间约束可以根据紧前关系、施工方向及活动类型分为多种场景。本文基于RSM法，针对可能出现的情况构造相应的约束。

1) 首日施工约束。

保证项目第一个活动的开始时间为0。本文以活动i的紧前活动集合Pi为空作为判断活动i为首日施工活动的依据。

2) 施工连续性约束。

重复性项目通常需要施工人员在各个单元间频繁移动，重复进行相同的工作。保持工作连续性能够提高人员工作效率、减少闲置费用[10]。因此，为保证各活动在施工过程中不发生间断，作如下约束。

3) 最小时间间隔约束。

根据本文提出的假设，活动间的时间间隔约束包含多种类型，具体约束类型需根据相邻活动的活动类型、施工区段来确定。由于条状活动可以看成一个跨度为0的块状活动 (bi=ei)，因此本文主要分析线性活动和块状活动之间的约束关系。活动b与其紧前活动a之间的最小时间间隔约束如下 (图1为最小时间间隔示意图，具体时间和里程的单位还需要根据具体工程项目确定)。

图1 活动间最小时间间隔约束Figure 1 Minimum time interval constraints between activities

当活动a和活动b均为线性活动时 (对应图1中场景1～ 4)，

当活动a为线性活动，活动b为条状活动时 (对应图1中场景5～ 6)，

当活动a为块状活动，活动b为线性活动时 (对应图1中场景7～ 8)，

当活动a、活动b为块状活动时 (对应图1中场景9) 。

4) 施工模式约束。

每个活动在各单元仅能采取一种施工模式。

5) 优先关系约束。

优先关系描述的是同一个单元中不同活动的施工先后顺序，优先关系约束要求任意活动i必须在其紧前活动全部结束后才能开始。

3 基于NSGA-II的算法设计

本文研究的问题属于NP难问题，因此选择带精英策略的非支配排序遗传算法 (non-dominated sorting genetic algorithm II，NSGA-II) 进行求解[12]。在标准NSGA-II的基础上，根据问题的特点开发了调度流程，并对遗传操作进行了改进，使新算法能够适用于大规模铁路进度计划优化。

3.1 染色体编码

染色体采用自然编码方式，随机生成初始种群。染色体第1部分表示施工模式ki,j，当工作量为零时 (Qi,j=0)，施工模式为0；反之，则在当前活动对应的施工模式集合Ki中随机选取。第2部分表示线性活动的施工方向ci，0为逆向施工，1为正向施工。染色体结构如图2所示。

图2 染色体编码方式Figure 2 Chromosome coding

3.2 适应度值

算法采用基于目标函数的非支配排序和拥挤度排序的适应度赋值策略，目标函数计算过程如下。

1) 工期计算。

通过调度流程计算得到各活动在各单元的开工时间Si,j、完工时间Fi,j和项目工期D。具体流程如下。

步骤1计算最早开工时间 ESi,j和最早完工时间EFi,j。首先根据施工模式计算各活动各单元的工期di,j，然后假设所有活动均在第0天开工，依据式(6)～ (7) 计算各子活动满足工作连续性的E Si,j和EFi,j。此时，根据首日开工约束，可直接依据式 (3)～(5) 得到首日开工活动Si,j和Fi,j。

步骤2计算最大推迟时间 MAXi，即各活动为满足与其紧前活动的最小时间间隔约束，需要在ESi,j、EFi,j的基础上往后推迟的时间。如图3所示，首先依据式 (8)～ (14) (不同场景的计算方式不同)，计算各单元节点处满足最小时间间隔约束的最早施工时间tlogic[b,j]，然后计算各单元节点推迟时间 ∆b,j，取最大值作为 MA。根据优先关系约束，当活动b存在多个紧前活动时，依次计算针对各紧前活动a(a∈Pb) 的M A，选取其中最大值作为M AXb。

图3 活动调度过程图Figure 3 Activity scheduling process diagram

步骤3计算各活动各单元最终开始时间Si,j和结束时间Fi,j。各活动在最早开工时间 ESi,j和最早完工时间E Fi,j的基础上推迟M AXi，得到Si,j、Fi,j、D。

以图1中场景1为例的活动调度流程伪代码如下。

2) 费用计算。

根据给定的任意施工方案，计算直接费用和间接费用。计算方法见式 (2)。

3.3 改进均匀进化精英选择策略

标准NSGA-II通过拥挤度和非支配排序，运用锦标赛法选择1/2的个体进入下一代[12]。为了保证种群对解的空间的充分探索，提高算法收敛性，本文将其改进为：前期在各支配层均抽取一定数量的个体，对各支配层由低到高选择种群个体数量依次递减，随着迭代次数的增加，选择个体的范围逐渐缩减，直到迭代至最后选取种群前1/2个体进入下一代。每一代选取个体数量的计算方式如式 (17)～ (18) 所示。

其中，r popr,g为从第g代第r个支配层选取的个体数量；npopg为第g代可选取的个体数量；θ为缩减比例，设置为0.8；Ng为第g代可选取的支配层级总数；pop为 种群规模；G为最大迭代次数；g为当前迭代次数；e表示自然对数函数的底数。

3.4 改进分层多策略自适应变异、交叉算子

NSGA-II采用了遗传算法的交叉、变异方式，在一定程度上降低了算法的收敛速度和效率。为提高算法性能，本文将差分进化算法 (differential evolution,DE) 的变异、交叉算子引入NSGA-II中。DE已被证明在大多数基准测试中，其性能优于遗传算法、自适应模拟退火和粒子群优化等算法[13]。

1) DE算法的变异、交叉算子。

差分进化算法利用N维向量表示一个种群Xg=[x1,g,x2,g,···,xpop,g]。目前常见的3种变异算子Rand/1、Best/1、Current to best/1，其变异方式为

其中，V为变异因子；xp1,g、xp2,g、xp3,g为从第g代种群中随机选择的3个个体，且p1 ≠p2 ≠p3；xbest,g为从第g代优秀个体中随机选择的个体，本文选取排序后种群的前10%作为优秀个体。Best/1倾向于探索能力，Rand/1倾向于开采能力，Current to best/1能够兼顾两种特性。变异因子V值越大，种群变异的步长越大，有利于提高种群多样性，增强全局搜索能力。V越小则开采能力越好，局部搜索能力越强。

交叉方式表示为

2) 多策略自适应变异、交叉算子。

为了平衡整个种群的开采能力和探索能力，本文依托上述变异算子的不同特性，设计了一种分层次、多策略、自适应的变异策略，来实现搜索能力的互补。首先，将种群根据支配等级和拥挤度排序等分为3层：精英层、普通层、劣势层，然后针对不同层次选取不同的变异策略和参数控制因子。

针对精英层，主要需要保持当前个体的优势，同时增强其局部探索能力，因此选择策略Best/1，设置V=0.8，C R=0.9。

针对普通层，主要目的在于探寻一些有潜力的解，进而增强种群的全局搜索能力，避免种群陷入早熟收敛，因此选择Rand/1，设置V=1.2，C R=0.8。

针对劣势层，其适应度较差，一方面应使其向优秀个体的方向进化，同时在一定程度上避免其陷入局部最优，因此选取策略Best/1、Rand/1混合使用，同时设置自适应参数。策略表示为

其中，αi为当前第i个个体对应的拥挤度。随着迭代次数不断增大，V、CR减小，加快种群收敛；同时引入拥挤度α，α较小时，当前个体周围解较为密集，此时提高V、CR有利于跳出局部最优，相反α较大时，适当降低V、CR以提高探索能力。

3.5 改进NSGA-II 算法框架

综上，具体计算步骤如下。

步骤1根据染色体编码规则生成种群规模为pop的初始种群。

步骤2依据活动调度和费用计算规则，计算各方案S适应度值。

步骤3进行非支配排序并计算拥挤度，依据均匀进化精英选择策略，选择p op/2个个体作为父代种群。

步骤4依据分层多策略自适应变异、交叉因子进行变异、交叉操作，得到子代种群。

步骤5合并父代种群和子代种群，得到合并种群，计算所有个体的适应度值，执行选择操作，得到下一代父代种群。

步骤6判断是否达到最大迭代次数G，若是，筛选得到非支配解集，算法结束；若否，转至步骤4。

4 实例分析

4.1 实例数据

某铁路工程十标段DK404+867～ DK432+908全长28 km，施工范围划分为6个单元，各单元起点分别为DK404+867、DK408+936、DK415+210、DK419+072、DK424+100、DK428+595。该项目中包含27个活动，各活动基本信息如表2所示，施工模式及费用信息如表3所示。对于铁路工程中的桥隧工程，由于其施工量和施工技术难度的限制，其施工工期基本固定，因此在表2中直接给出了工期数据，在表3中省略了施工速率。项目间接费用率为24 000 元/d。

表2 活动基本信息Table 2 Basic information of activities

表3 活动各施工模式速率及费用率Table 3 Rates and cost rates of various construction modes of activities

4.2 优化方案

利用改进的NSGA-II算法，采用Matlab2016b实现，在操作系统为Windows10，处理器为Intel Core i5-8250U，CPU主频为1.80 GHz的环境下运算，取种群数量 pop=90，迭代次数G=900，得到7个工期-费用权衡最优的进度计划方案S1～ S7，各方案对应的项目总工期和总费用如表4所示。

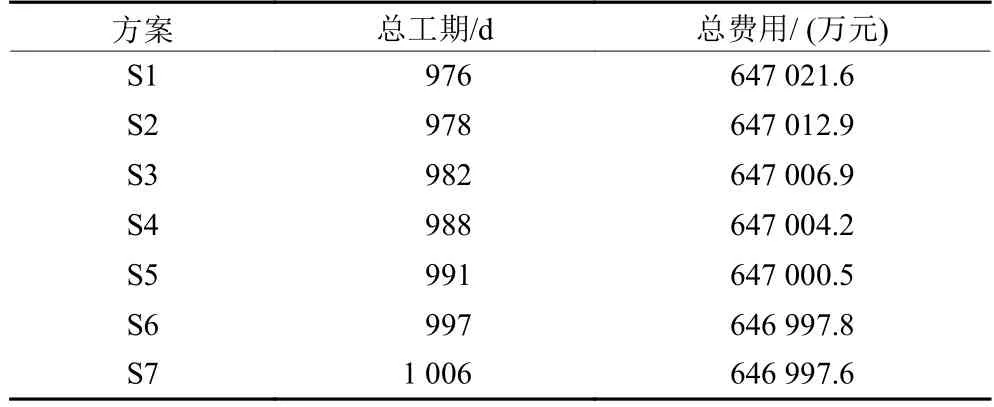
表4 Pareto解集Table 4 Pareto solution set

由图4可知，本文提出的模型和算法在一次运行中自动生成构成Pareto前沿 (pareto front，PF) 的所有可能的非支配解，确保了对解空间的充分探索。相较于将工期-费用均衡综合为一个目标函数，最后生成一种施工方案，本文提出的方法能够获得更加丰富的工期-费用最优方案，使决策者能够根据需求从中选取合适的方案。例如，若唯一的优化目标是工期最小化，则方案S1将是最佳方案，该方案工期最短，总工期为976 d，但对应最高费用647 021.6万元；若优先考虑费用因素，则应选择方案S7，该方案的总费用646 997.6万元，对应最长工期1 006 d。表5和表6为方案S1的具体施工方案，表5中的数据表示“ (开工时间，完工时间) 施工模式”。图5为对应的进度计划图。

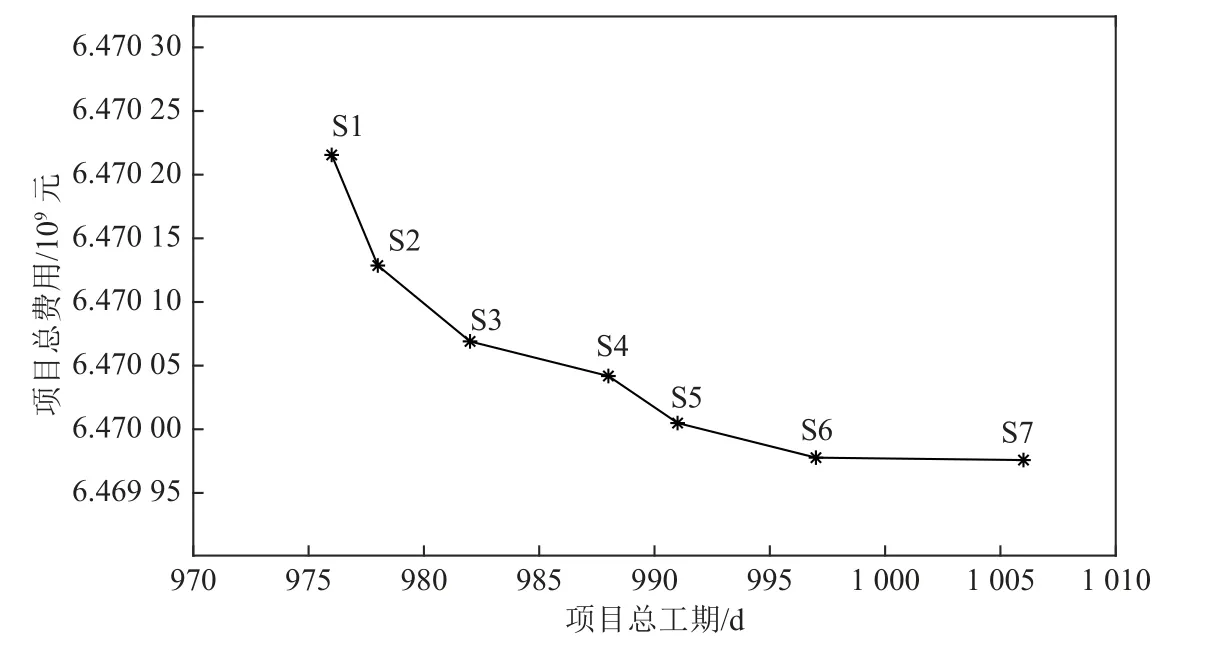
图4 总工期-总费用Pareto曲线Figure 4 Pareto curve of total costs with the construction periods

图5 S1进度计划图Figure 5 Schedule diagram of S1

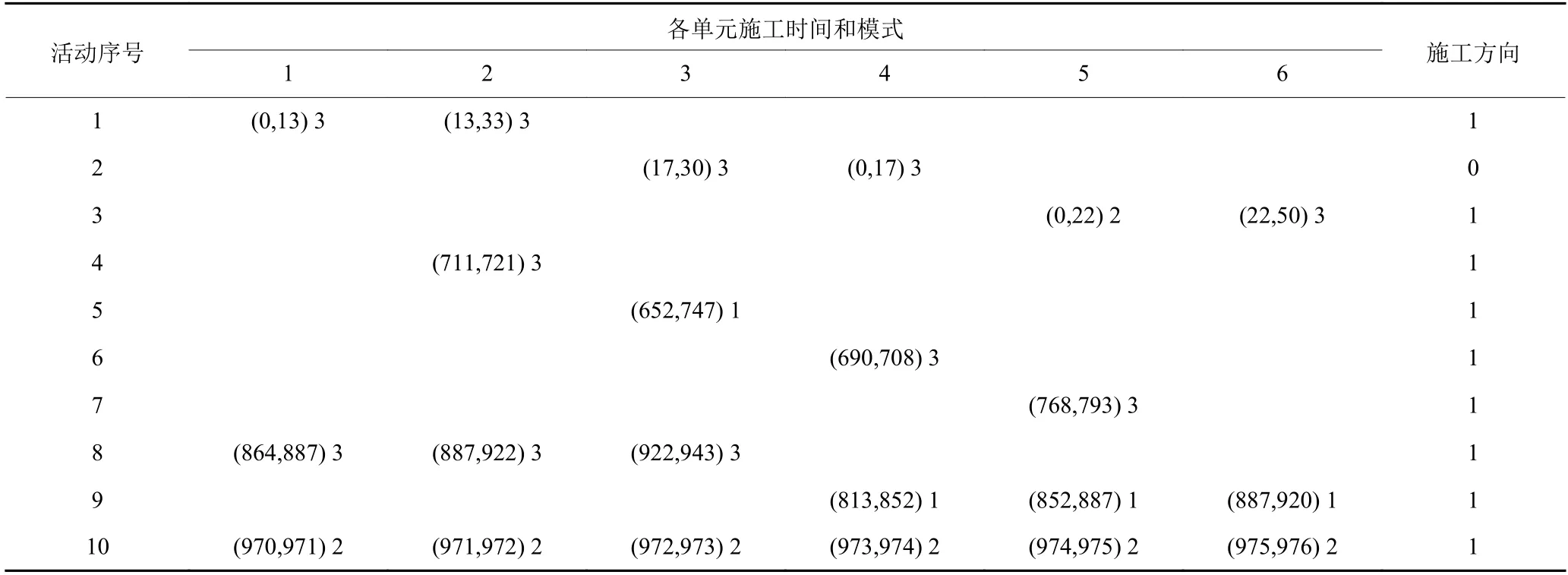
表5 S1线性活动施工方案Table 5 Linear activity construction scheme of S1

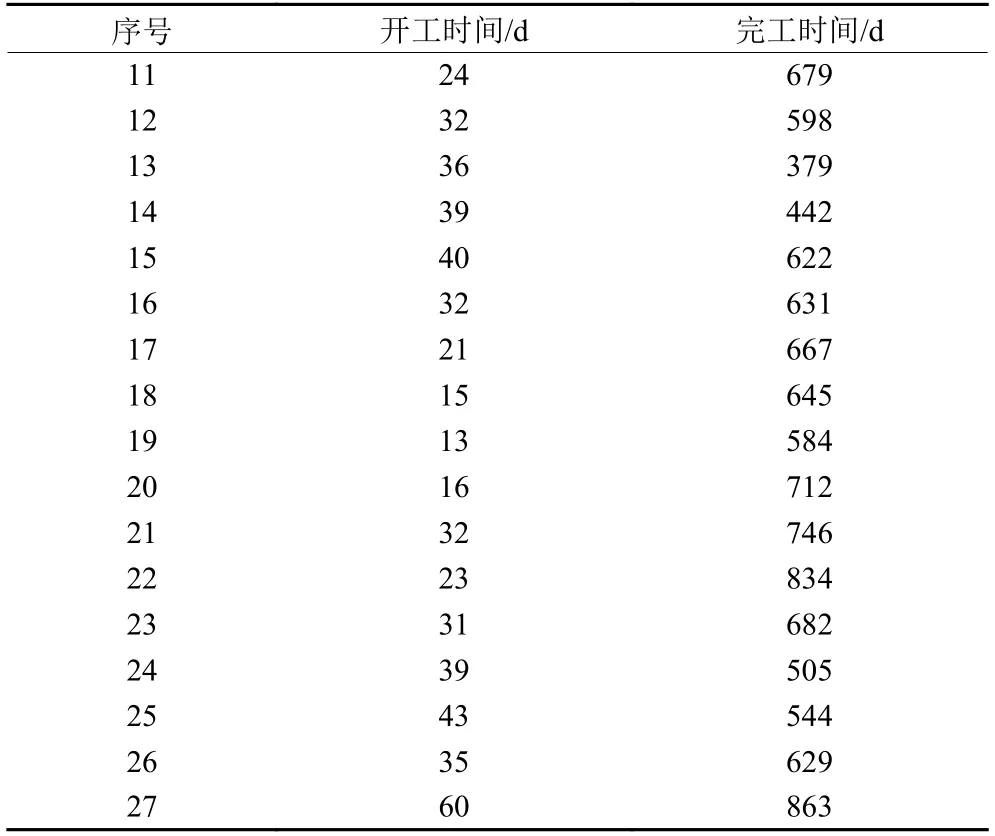
表6 S1条块活动施工方案Table 6 Strip and block activity construction scheme of S1

4.3 算法性能比较分析

本文选择综合指标超体积 (hyper-volume，HV)作为评价指标，反映算法的收敛速度、PF的均匀性和宽广性等。HV计算的是参考点和PF构成的不规则图形的面积，HV越大，则所获得的PF越接近真实PF[14]。

为进一步测试本文提出算法的优化性能，本文将产生不同规模的算例，对算法进行更深入的分析。本文按照以下步骤随机生成算例。

步骤1确定问题的规模，主要为项目活动个数I与施工单元数目J;

步骤2随机生成任意活动i的相关参数，包括表2、表3所列数据。

本文对于不同规模的4组算例分别使用NSGAII和本文算法以相同种群规模、迭代次数及运行环境进行求解。表7为两种算法独立运行25次所得到的实验结果，其中，HV平均值反映了求解精度，HV方差反映了算法稳定性。可见，改进后的算法得到的PF分布更均匀宽广，具有良好的稳定性。

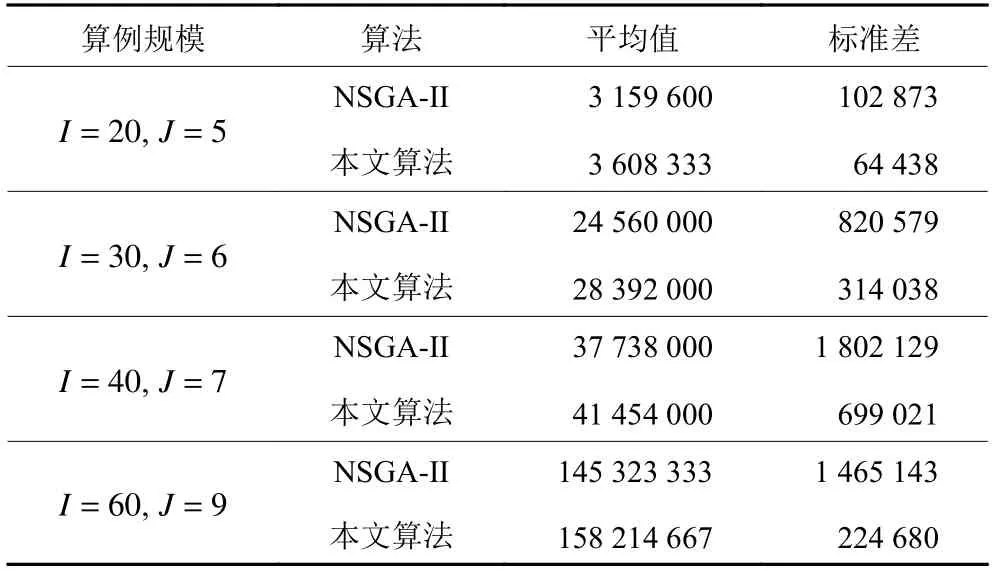
表7 不同规模各算法获得HV平均值及标准差Table 7 The mean and standard deviation of HV obtained by various algorithms of different scales

将不同规模下各算法独立执行 25 次所获最大HV时对应的HV收敛曲线进行对比，如图6所示，可得本文算法收敛速度更快，且针对较大规模的算例仍能保持良好的收敛性。

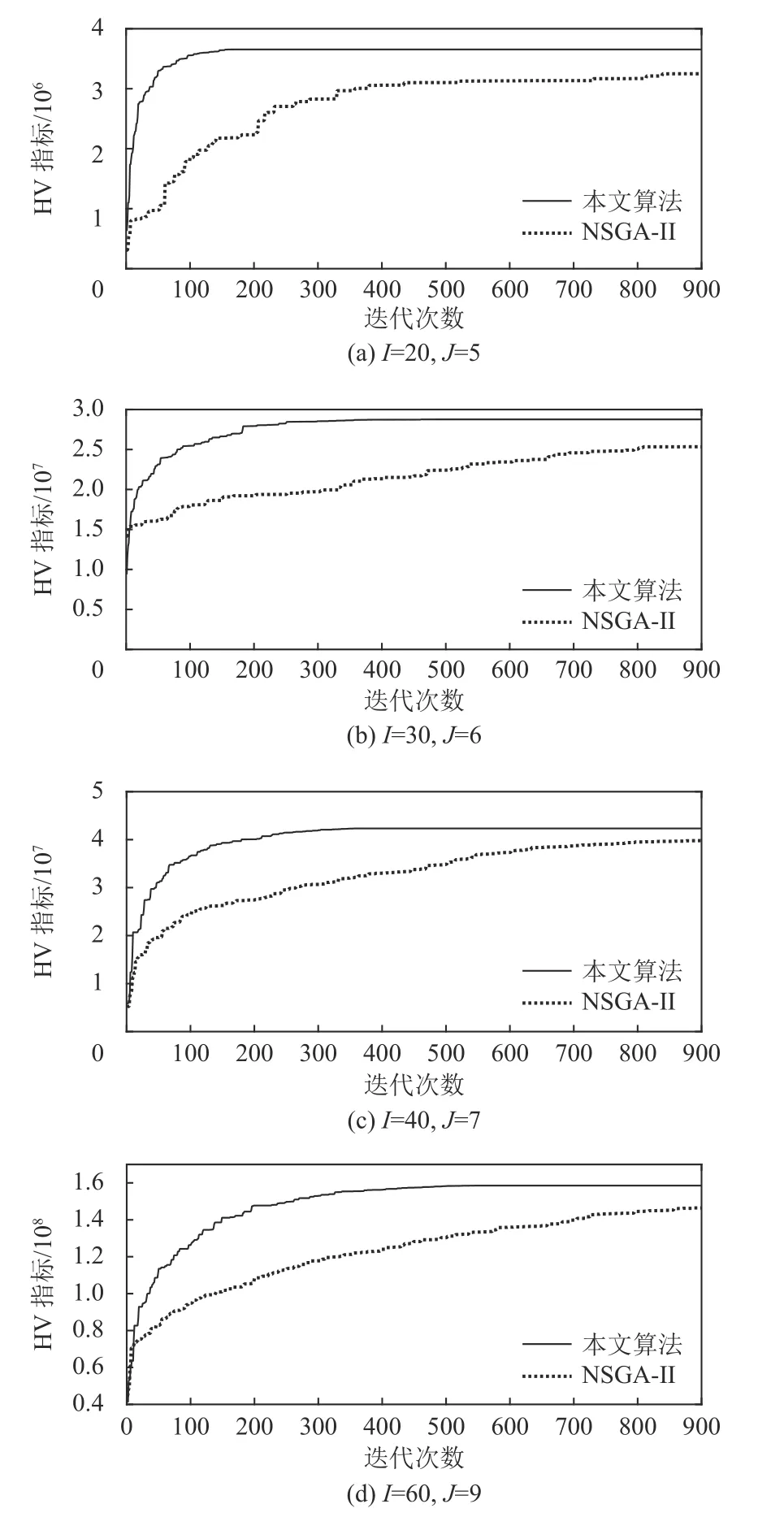
图6 不同规模各算法HV进化过程Figure 6 Evolution process of HV with various algorithms at different scales

5 结论

本文基于RSM方法，结合我国铁路建设活动的实际特点，考虑了施工方向和特殊活动对施工方案的影响，构建了工期-费用多目标优化模型。相较以往只考虑正向施工线性活动，本文针对活动类型的拓展，增加了可行施工方案的数量，大大增强了模型对于铁路项目的适用性。在模型的求解过程中，设计了均匀进化的精英选择策略，引入差分进化的变异、交叉算子，构造了分层多策略自适应的变异、交叉算子改进NSGA-II算法获得Pareto解集，决策者可根据实际情况和需求从中选取合适方案。文中以一个实例验证了本文所提出模型和算法的有效性。最后，通过求解不同规模随机算例，与传统NSGA-II对比，结果显示改进NSGA-II收敛速度更快，解的质量更优，运行更加稳定。

本研究假定所有子活动只能按照一个固定的顺序进行施工，而在实际工程中，可能存在活动上各子活动之间的逻辑施工顺序是可变的情况[7]。因此，后续的研究将增加对软逻辑、多工作队等因素的考虑，使模型算法能适应情况更加复杂的场景。