利用本地频率线性分量的电力系统功率缺额估计方法

秦颖婕，李文博，伍双喜，李佳朋，谭嫣，李宇骏

（1. 广东电网有限责任公司电力调度控制中心，广州 510060；2. 西安交通大学电气工程学院，西安 710049）

0 引言

近年来，新能源发电以其清洁、可再生等优势得到了大力发展，随着电力电子换流器型电源（converter-interfaced generators，CIGs）占比的提升，电网的惯量水平不断下降，频率稳定问题日渐突出［1-3］。换流器型电源具有控制灵活、响应迅速的优点，利用这一特点可以快速调整换流器型电源的出力，减少系统中功率缺额，从而降低系统频率偏移、提升系统频率稳定性［4-6］。为实现这种控制结构，需要开展系统功率缺额的快速估计。系统功率缺额可以通过系统总惯量乘以惯量中心（center of inertia，COI）频率变化率获得，在系统总惯量已知的情况下，系统功率缺额估计依赖于COI频率变化率（rate of change of frequency，ROCOF）的快速计算。

COI 频率可以通过许多方法获得，主要分为两类：单机等值模型法和多机模型法。传统的单机等值模型将原始多机系统进行单机等值聚合，仅用平均频率近似描述系统的动态过程。文献［7］对各发电机频率按其惯性常数做加权平均，提出了系统平均频率模型（average system frequency，ASF）。文献［8］将ASF 模型扩展至含频率控制的风力机组，并计及了负荷的频率与电压特性。为简化分析，文献［9］将系统内所有发电机调速器等值为单台调速器特性，提出了系统频率响应模型（system frequency response，SFR），并导出了系统频率的解析表达式。基于SFR 模型，文献［10］提出了自适应低频减载方法，实现了功率缺额的快速估算与功率缺额在所有切负荷轮次间的合理分配。文献［11］进一步考虑了系统旋转备用容量、负荷频率特性等因素的影响，提出了改进的SFR 模型，提高了系统功率缺额的计算精度。文献［12］考虑风机参与调频，推导了风机运行在减载和最大功率跟踪方式下系统的单机等值频率模型。采用单机等值模型法估算系统功率缺额时，认为任意母线测量频率可近似替代系统频率，这一假设忽略了系统暂态过程中多机间转子的摇摆，可能使功率缺额估算不准确，甚至会导致预测不平衡功率方向的错误。

多机模型法考虑了发电机转子间的相对摇摆和频率在空间中的分布特性，现在已经成为研究这一问题的主流方法。文献［13］采用惯量中心坐标建立模型，通过多机系统的仿真轨线获得关键系频率特性参数，弥补了单机等值模型法的局限性。文献［14-15］利用广域测量测得的发电机相关电气量数据，使功率缺额的估算不依赖于数值仿真。文献［16-17］通过广域测量系统测得系统中少部分特定母线的频率，再通过这些信息估计COI频率。文献［18］考虑了风机的虚拟惯量对COI频率的影响，进一步提升了功率缺额估计的精度和鲁棒性。但是，此类方法不仅需要通信，而且广域测量数据不一定能保证系统完全能观，会导致估计的功率缺额不准确。为了克服这些问题，国内外学者开始探索通过本地频率快速估计惯量中心频率，文献［19］指出本地频率在其拐点处与COI频率近似相等，然而这一性质只在两机系统中得到证明。类似地，文献［20］提出了基于本地频率偏移面积的功率缺额估算方法。前一种方法需要等待两个频率拐点，后一种方法需要较长的时间窗才能满足精度要求，这两种方法耗时较长，因此并不适合系统功率缺额的快速估计。

本文聚焦于基于本地测量信息的COI频率估算方法。首先，证明了在系统受扰初期，本地频率变化量的线性分量与COI 频率变化量相等这一性质。然后，基于最小二乘拟合提取本地频率变化量线性分量实现了快速的功率缺额估计。最后，在新英格兰39节点测试系统上验证了所提方法的有效性。

1 多机系统线性化模型

1.1 COI频率与系统不平衡功率

在一个有n台发电机的电力系统中，描述每台发电机动态行为的转子运动方程可以表示为：

式中：Hi为第i台发电机的惯量时间常数；ωi为第i台发电机的角速度；ωB为系统的基准频率；δi为第i台发电机的功角；Pmi和Pei分别为第i台发电机的机械功率和电磁功率标幺值；n为发电机数量。在标幺制下，角速度与频率的大小相等，下文中将用发电机频率代指角速度。为了便于描述多机系统在受扰后的动态行为，常在惯量中心坐标下进行建模分析。将系统内所有发电机转子运动方程中的第一式相加，可得COI摇摆方程为：

式中：HCOI为系统总惯量；ωCOI为惯量中心频率，其定义为：

在系统受扰初期，可以认为调速器还未启动，发电机的机械功率不发生变化。因此，将式（2）改写为如下形式。

式中：ΔωCOI为COI 频率变化量；Pd为系统功率缺额。将式（3）左右两边同时从0~t时刻进行积分，可得：

式中：Δωi为第i台发电机的频率偏差。式（4）表明，COI 频率变化量与系统不平衡功率及系统总惯量有关，且在系统受扰初期呈线性变化。

1.2 多机系统线性化模型

本文主要关注系统受扰初期的动态行为。首先，将所有负荷等效为阻抗，并入节点导纳矩阵中，使用Kron 节点消除技术消除网络中除去发电机内电势节点外的所有节点［21-22］，消除后的节点导纳矩阵记为Y。对于发电机内电势节点，其节点注入功率与节点注入电流及节点电压之间的关系为：

各节点注入电流可由节点电压方程计算。

式中Y=。

将式（6）取共轭后代入式（5）可得：

式中：下标i、j为发电机的序号；Yij为导纳矩阵Y第i行j列的元素；Qei为发电机i注入电网的无功功率。电压向量用极坐标形式表示为：

式中：Ei和δi分别为发电机内电势电压的有效值与相角，并且该电压相角等于发电机功角。将导纳矩阵中的元素用直角坐标的形式表示。

则式（5）可以写为：

对式（10）使用欧拉公式，并进行虚实部分离，则在扰动发生前，系统中各台发电机的电磁功率可以由式（11）给出。

式中：Ei、Ej分别为第i台、第j台发电机的内电势；Gij和Bij分别为发电机i、j之间的转移电导和转移电纳；δij为发电机i、j的功角差。通过泰勒展开将上式线性化，可得：

式中：δij（0）为发电机i、j的功角差初始值；Δδij为发电机i、j功角差的变化量。根据式 （12），可得每台发电机的电磁功率变化量为：

式中：

式中：Pei（0）为电磁功率的初值，在稳态时该值等于发电机的机械功率。

联立式（1）和式（13）可得：

记为：

式（15）中矩阵A（0）含有2n个特征根。一般来说，如果忽略发电机阻尼，系统正常运行时矩阵A（0）有两个零根、n-1 对共轭复根［23］。其中一个零根是由式（16）引起的。

另一个零根则是由忽略系统阻尼引起的。通过选取一台机作为参考，可以消去这两个零根，不妨假设第n台机为参考机。将式（15）的前n-1行与第n行相减，构造新的状态向量，式（15）可化为2n-1阶微分方程，并消去其中一个零根，化简后的微分方程如式（17）所示。

式中：

将式（17）第n行到第2n-2 行与第2n-1 行相减，构造新的状态向量，式（17）可化为2n-2 阶微分方程，消去另外一个零根，化简后的微分方程如下。

式中 ：A的表达式如式（18B）所示；x=[Δδ1n…。

2 基于本地频率的功率缺额快速估计方法

系统发生线路故障、发电机脱网等事故时，会产生功率缺额。快速估算功率缺额可以评估事故规模，并指导频率稳定控制。现有功率缺额估算方法大都依赖通信以获取系统惯量中心频率，存在通信延时且可靠性较低。针对这一问题，本节提出了基于本地频率信息的系统功率缺额估算方法。

2.1 本地频率线性分量性质

在系统受扰后，网络结构的改变使得发电机的电磁功率产生突变并与机械功率产生偏差，即Pe（i0）≠Pm（i0）。因此，式（18）可以重写为：

对式（19）求一阶导使得原微分方程齐次化。

由于发电机的功角和转速均不能突变，因此x的初值为零。基于式（19），ẋ的初值为：

为了求解微分方程初值问题式（20）、（21），构造如下的线性变换。

式中：XR∈C2(n-1)×2(n-1)为由矩阵A的所有右特征向量构成的矩阵。基于式（22）和（20），可得：

式中：λ1，λ2， ⋅⋅⋅，λ2n-2为矩阵A的特征值。由于状态变量z中各分量解耦，式（23）中含有2n-2 个独立的一阶线性微分方程，易得式（23）的解为：

基于式（22）和（23），原方程的解为：

矩阵A有n-1 对共轭复根，对应着系统的n-1个机电模式。根据式（25），各发电机频率变化量与参考机频率变化量之差均可表示为n-1 个机电模式的线性组合。

式中：c2，k为第k个振荡模式的振荡频率；c1，ik和c3，ik分别为第k个振荡模式在Δωin中正、余弦分量的幅值。

将式（26）中第i个方程乘以Hi，然后再将这n-1个方程相加可得：

式（27）左右两端同时除以HCOI，并将式（4）代入，则第n台机的频率变化量为：

类似地，选择不同的发电机作为参考机，每台发电机的频率变化量都可以被表示为：

式中：c4，ik和c5，ik分别为第k个振荡模式在Δωi中的幅值和相位。由式（29）和式（4）可知，本地频率变化量的线性分量与COI频率变化量相等。

根据前文所述，在电力系统中，本地频率变化量的线性分量与扰动后一段时间内的COI频率变化量相等。基于这一性质，通过提取任意本地频率的线性分量，可以快速获取COI频率变化率并实现系统功率缺额估计。

2.2 基于最小二乘拟合的系统功率缺额估计方法

通过最小二乘拟合，可以提取任意本地测量频率的线性分量。具体来讲，需要构造一个拟合函数p(x)，作为定义在点集X={x1，x2， ⋅⋅⋅，xm}上列表函数f(x)的近似表达式，并使得拟合函数与原列表函数的误差在某种意义上达到最小。最小二乘拟合技术以误差二范数平方为衡量指标，用这种方式求得的拟合函数在每个点上与原列表函数的距离di=p(xi)-f(xi)的平方和最小。

令｛（t1，y1），（t2，y2），···，（tm，ym）｝为采样得到的本地频率变化量的时间序列。由式（29）可知，本地频率变化量的线性分量可通过求解以下优化问题获得。

式 中 ：t=[t1，t2， ⋅⋅⋅，tm]T，y=[y1，y2， ⋅⋅⋅，ym]T为采样序列，k，ai，bi，ci，i∈{1，2...n-1}为决策变量。式（30）是一个非线性优化问题，可以使用梯度下降算法进行求解。梯度下降是迭代法的一种，可以用于求解非线性最小二乘拟合问题，其主要思想是沿着函数梯度下降的方向进行搜索，经过多步迭代后收敛到函数最小值附近，因其简单、求解效率高等优点，已成为求解无约束优化问题时最常采用的方法之一。

根据式（4），在系统惯量已知的情况下，系统的功率缺额估计由下式给出。

式中̂为由式（30）得到的COI频率变化率。

3 算例分析

为了验证所发现特性的正确性和所提系统功率缺额估计方法的有效性，在新英格兰39 节点系统上进行了测试。该系统额定频率为60 Hz，容量基准值为100 MVA，总装机容量为7 367 MW，总有功负荷为6 254.2 MW，负荷模型分别采用恒阻抗与恒功率模型。系统拓扑如图1 所示。测试系统的详细参数可参见文献［24-25］。

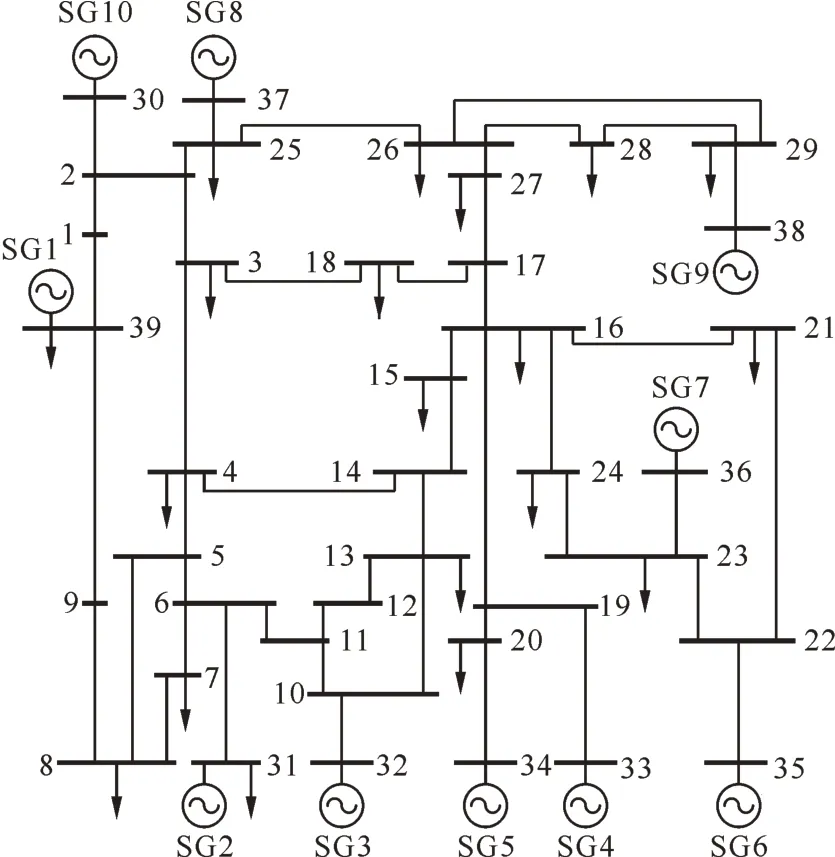
图1 新英格兰39节点系统拓扑示意图Fig.1 Sketch diagram of New England 39-bus system

首先，负荷模型采用恒阻抗模型。图2 为0 时刻时节点21 处发生负荷突增，系统产生3.6 p. u.有功功率缺额时各发电机的频率响应。从图1 可以看出，在扰动发生后1 s 内，COI 频率呈线性下降，每台发电机的频率均在COI频率附近振荡。

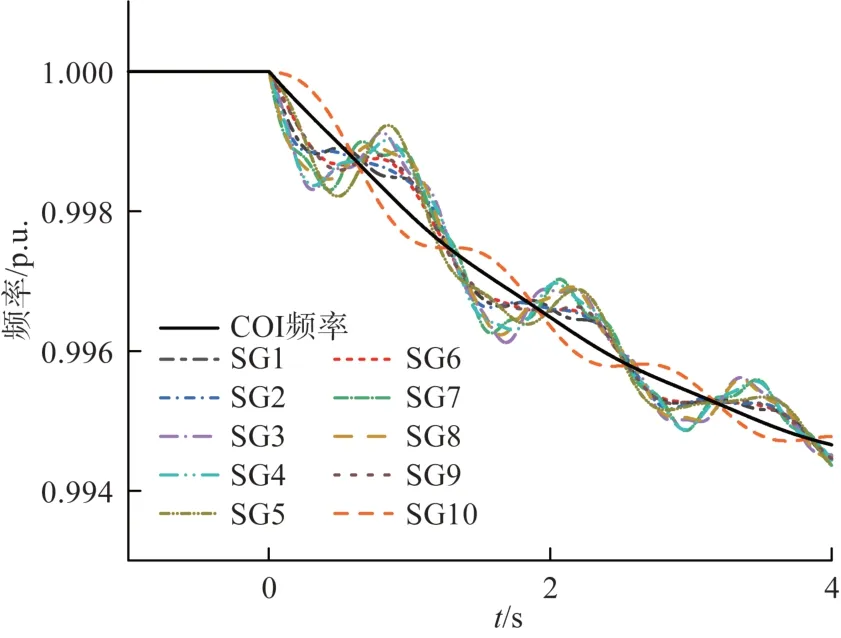
图2 负荷突增后测试系统频率响应Fig.2 Frequency response of the test system following a sudden load increase

本文所提的快速功率缺额估计中，时间序列的采样频率为1 kHz，时间窗长为0.8 s。7 号发电机的动态响应如图3 所示。从图中可以看出通过拟合得到的本地频率（黑色虚线）非常接近实际本地频率（绿色实线），通过求解式（30）提取的本地频率的线性分量（橙色虚线）几乎与COI 频率（红色实线）相等。

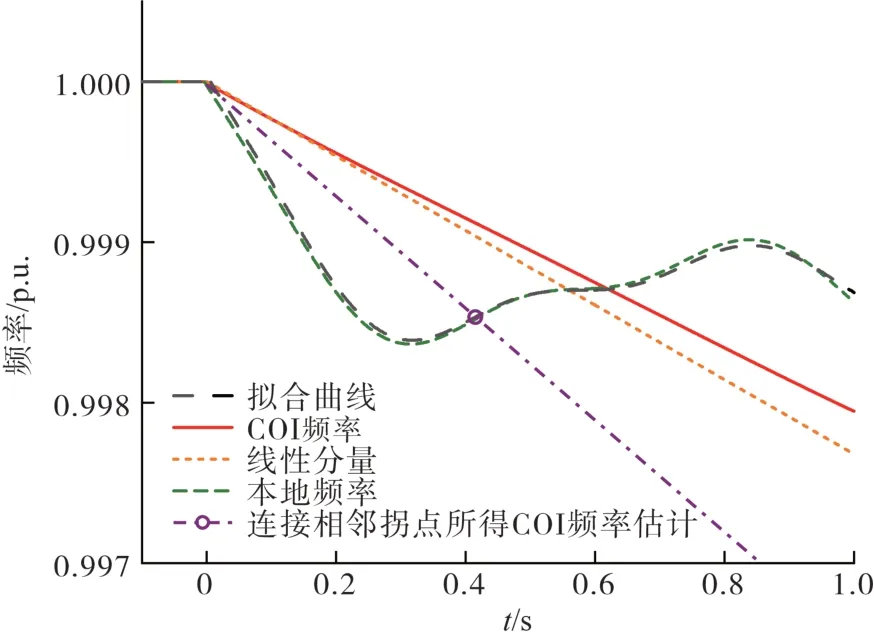
图3 负荷突增时7号发电机频率响应Fig.3 Frequency response of SG7 following a sudden load increase

除此之外，文献［19］通过本地频率每两个相邻拐点的连线来近似COI 频率曲线，其估计结果（紫色实线）如图3 所示。采用该方法估算的COI 频率与实际COI频率的偏差较大。如果连接之后的相邻拐点，甚至会产生错误的结果。

表1展示了节点24处负荷有功功率突增时，系统功率缺额估计结果。

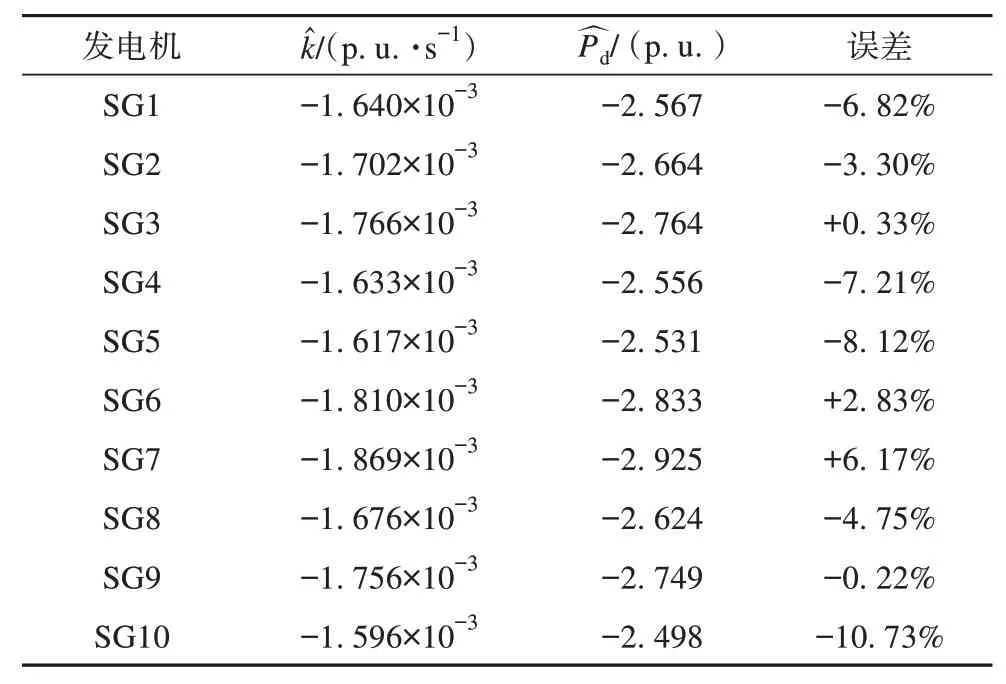
表1 节点24负荷突增时的系统功率缺额估计结果Tab.1 System power deficit estimation result following a sudden load increase at bus No.24

如表1 所示，不同发电机节点估算的功率缺额与真实值的误差基本在10%以内。估计误差的产生原因主要包括两个方面：1）分析模型中线性化引入的误差；2）忽略受扰初期机械功率变化引入的误差。值得注意的是，进行功率缺额估计的主要目的是为快速调节新能源出力提供依据，减小功率缺额，从而降低频率偏移，现有方法均不能精准补偿功率缺额，但可以显著改善频率暂态特性。应用于旨在为新能源调频提供参考的快速不平衡功率估计时，估计误差在可接受范围内。

负荷采用恒功率模型时，所提算法仍然能较为精确地估计有功功率缺额。图4、图5 分别为负荷采用恒功率及恒阻抗建模、节点15 处负荷有功突增导致系统中产生 3.0 p.u. 有功缺额时，9 号发电机的频率响应和拟合结果，该场景下所提算法误差仅为约+6.24%和+5.51%。从图4 和图5 的对比中可以看出，所提算法对不同的负荷建模有较好的适应性。

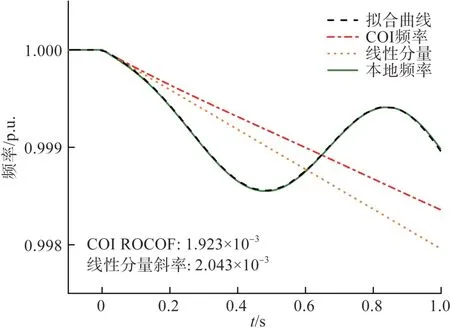
图4 负荷突增时9号发电机频率响应（恒功率负荷）Fig.4 Frequency dynamic of SG9 following a sudden load increase （constant power load）

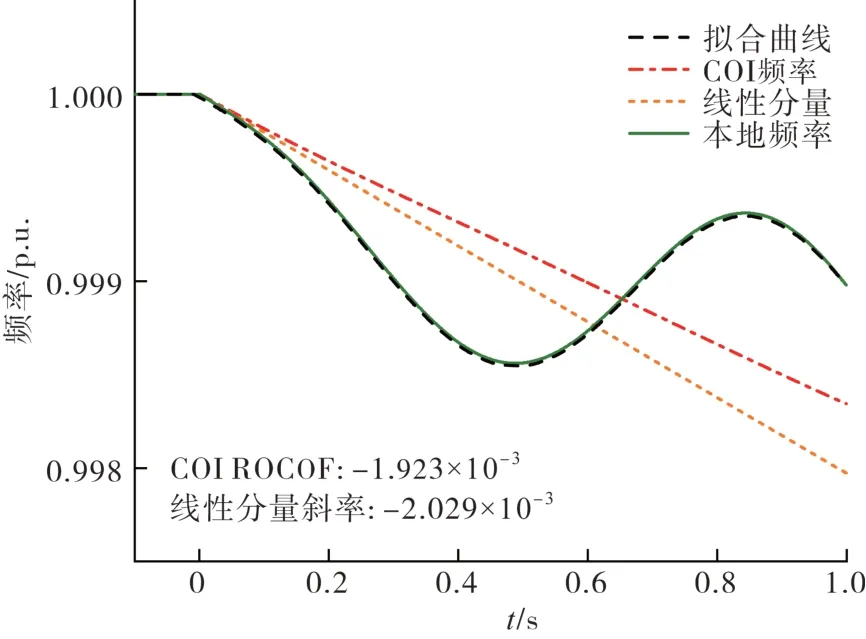
图5 负荷突增时9号发电机频率响应（恒阻抗负荷）Fig.5 Frequency response of SG9 following a sudden load increase （constant impedance load）

图6、图7 分别为负荷采用不同模型，节点15处负荷突增导致系统中产生 5.0 p.u. 有功功率缺额时9 号发电机的频率响应和拟合结果。两种情况下，所提方法的不平衡功率估计误差分别为+1.38%和+4.45%，从拟合结果可以看出，该方法对不平衡功率大小有较好的适应性。

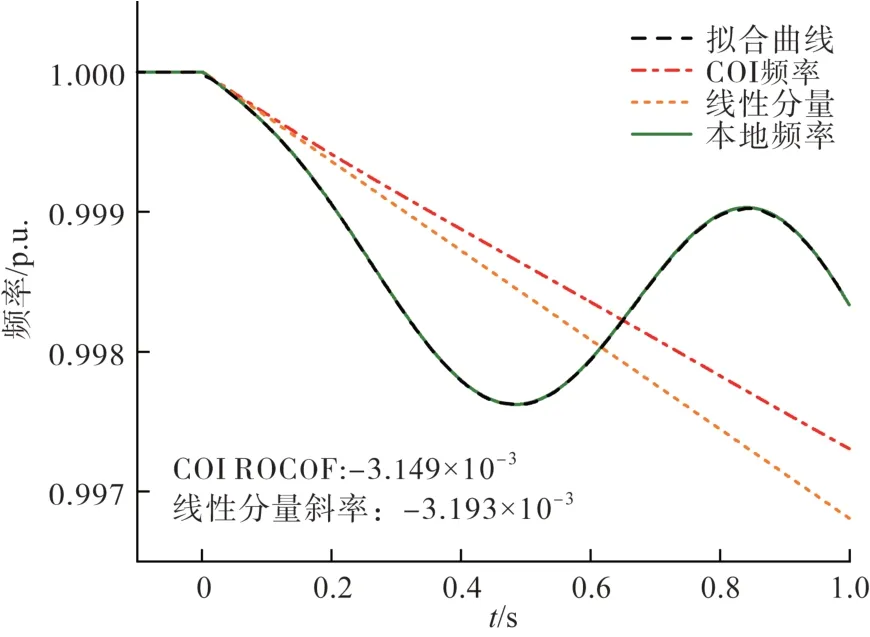
图6 负荷突增时9号发电机频率响应（恒功率负荷）Fig.6 Frequency response of SG9 following a sudden load increase （constant power load）

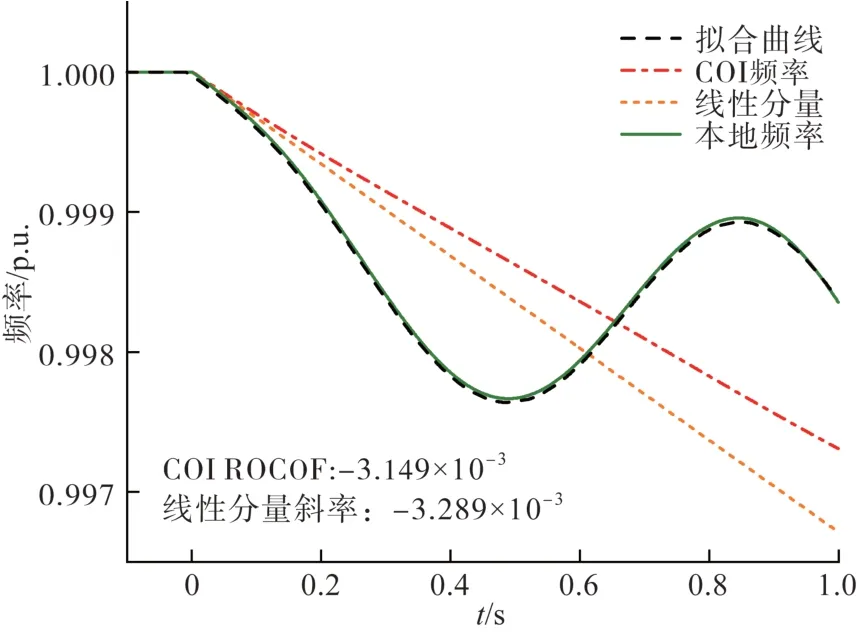
图7 负荷突增时9号发电机频率响应（恒阻抗负荷）Fig.7 Frequency dynamic of SG9 following a sudden load increase （constant impedance load）

表2为负荷采用恒功率模型、节点15处负荷突增并产生-3.887 p. u. 实际有功缺额时由各发电机频率估计所得的有功功率缺额估计结果，此场景下不同发电机处估计的功率缺额与真实值的误差仍然在10%以内。如表1—2 所示，由各发电机频率估计所得的功率缺额与实际值的平均误差为-4.51%，该方法具有很高的应用价值。

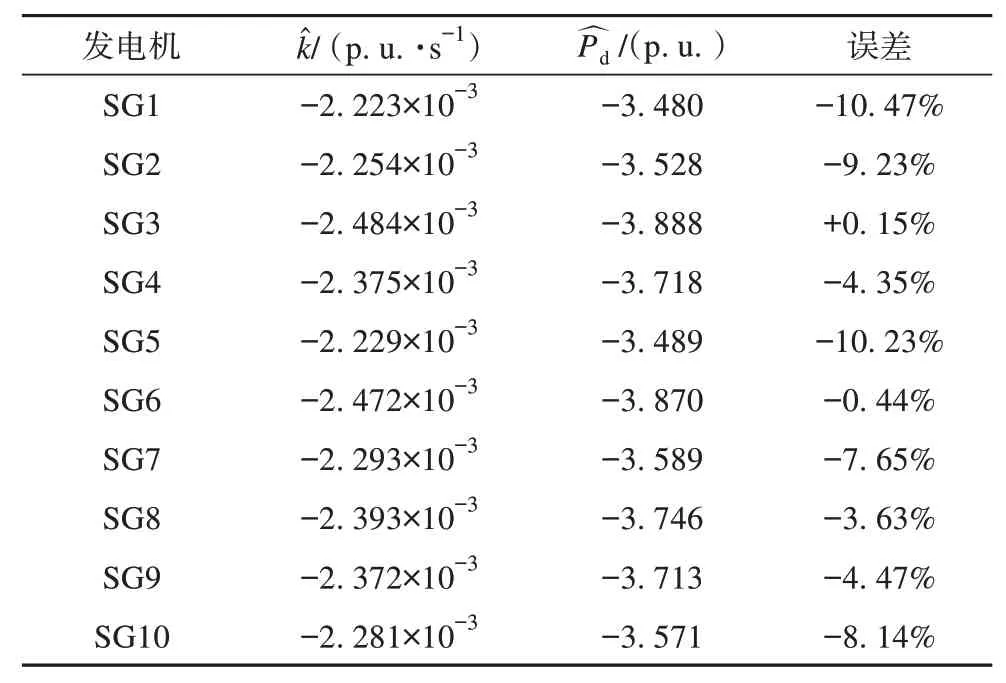
表2 节点15负荷突增时的系统功率缺额估计结果Tab.2 Estimation result of system power deficit following a sudden load increase at bus No.15

此外，当系统功率过剩时，所提方法仍能较好的估计出过剩功率的大小。图8所示为0时刻节点15处负荷突降，系统中产生2.9 p.u. 有功过剩时所有发电机的频率响应。从图8 可以看出，当系统中存在功率过剩时，在扰动后1 s内COI频率基本呈线性上升，每台发电机的频率均在COI频率附近振荡。

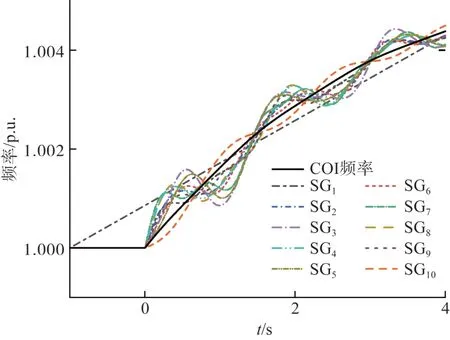
图8 负荷突降后测试系统频率响应Fig.8 Frequency response of the test system following a sudden load decrease

该场景下6号发电机的频率响应如图9所示。

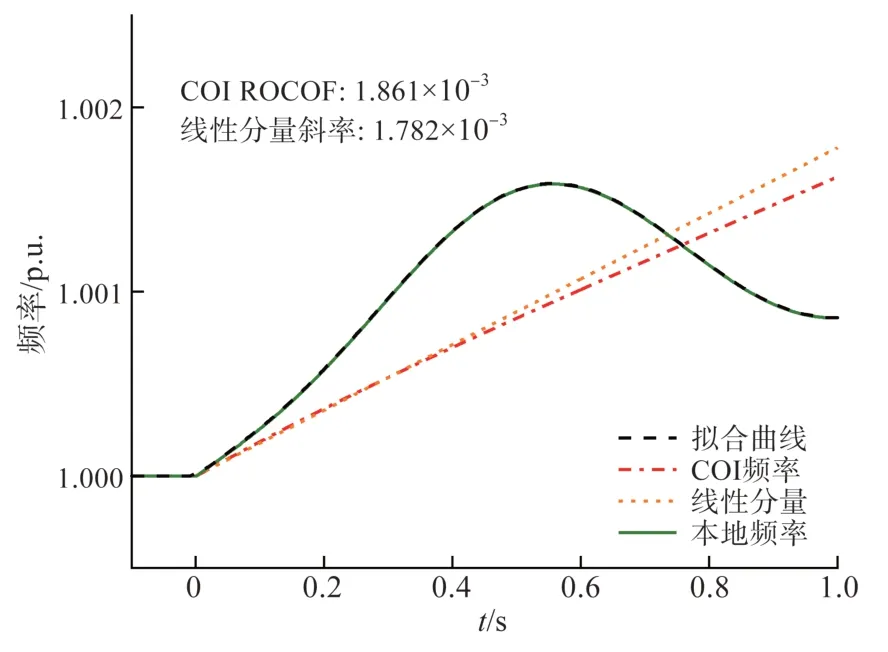
图9 负荷突降时6号发电机频率响应Fig.9 Frequency response of SG6 following a sudden load decrease

从图9 可以看出，拟合曲线与本地频率曲线基本重合；6 号发电机频率曲线中提取出的线性分量斜率为1.782×10-3p.u./s，与惯量中心频率变化率十分接近。所提方法也适用于系统中存在功率过剩时的不平衡功率估计。

4 结语

本文首先证明了在系统受扰初期所有发电机频率变化量的线性分量与COI频率变化量相等。利用这一性质，提出了一种基于本地频率的系统功率缺额估计方法。

该算法利用最小二乘拟合提取本地频率的线性分量，实现了无需实时通信的快速系统功率缺额估计，有利于充分利用CIGs 的快速功率调节能力，提高系统频率稳定性。最后在新英格兰39 节点测试系统上证明了该方法的有效性。