基于随机森林与内核岭回归的配电网线损在线计算

王华佳，曹文君，张岩，于丹文，李付存，于一潇

（1. 国家电网山东省电力公司电力科学研究院，济南 250003；2. 电网智能化调度与控制教育部重点实验室， 山东大学，济南 250061）

0 引言

线损是衡量电网运行经济性一项重要指标［1］，而线损计算是配电网运行管理的重要依据之一。随着负荷的不断增长，配电网电能损耗问题日益突出，精准的线损计算对优化电力网络设计、提高配电系统运行的经济性具有重要的指导作用［2-3］。

广泛使用的线损计算方法有潮流计算法、均方根电流法以及等值电阻法等［4］，这些方法依赖潮流计算，需要采集系统中所有节点的电气量才能得到线损［5］，但由于配电网自动化水平较低以及分布式发电（distributed generation，DG）并网等原因，在输电网中得到广泛应用的线损计算方法并不适用［6］。实际应用中，配网各节点的电气量采集间隔不尽相同，而完成一次潮流计算的时间间隔取决于采集间隔时间最大的节点，因此当线损计算实时性要求较高时，传统的基于潮流的计算方法将难以胜任。

针对线损的在线计算已有一定的研究基础。文献［7］在现有信息采集及线损计算系统的基础上，对信息采集、主站系统、通信信道、系统接口进行重新设计，实现了线损在线监控。文献［8］提出了一种基于公共信息系统的在线计算理论线损的数据共享方案，该方法能够充分利用电力SCADA、配电网GIS 等信息，自动形成用于线损理论计算的计算模型。上述文献虽然建立了配电网线损在线计算的模型，但这些模型都依赖于完备的信息采集系统，对配网自动化水平的要求较高。近年来随着机器学习的发展［9-11］，基于人工智能算法的配电网线损计算逐步成为新的研究热点。文献［12］提出了基于BP 神经网络的配电台区线损计算方法，首先基于K-means 对配网台区进行分类整理，然后使用BP 神经网络预测配电台区线损功率。文献［13］提出了基于特征选择与集成学习的配电网线损预测方法，为配电系统能量管理提供依据。文献［14］基于K-means 聚类和径向基（radial basis function， RBF）神经网络的配电网线损计算模型，通过正交最小二乘法优化神经网络，提高了线损计算精度。文献［15］提出了基于免疫遗传算法的BP 神经网络计算配电网线损，通过引入免疫机制缓解了遗传算法搜索效率低的缺点，遗传算法的引入提高了BP 神经网络的收敛速度。上述基于机器学习理论的配网线损计算均未考虑配电网数据缺失的情况。

本文基于随机森林（random forest，RF）以及内核岭回归（kernel ridge regression，KRR）方法建立配电网线损在线计算模型。RF 分类方法能够依据数据集的某些特征将其分类［16］；KRR 方法则能够学习两个数据集之间的非线性映射关系，并通过映射关系根据一个数据集中的数据预测另一个数据集［18］。在接入DG 的情况下，负荷除了从根节点汲取能量外，也可以从DG 获得电能，所以配网线损功率与节点负荷功率、DG 出力、系统根节点出力存在复杂的非线性映射关系。本文借助RF 的分类能力以及KRR 的学习能力，采用“离线训练，在线应用“的方式计算线损。本文主要贡献如下。

1）提出了基于KRR 方法的配网线损在线计算模型，离线训练时充分挖掘节点负荷功率、DG 出力与线损功率之间的非线性映射关系，在线应用时根据此映射关系得到各支路线损功率。

2） 提出了在某些节点数据不能获取情况下的配电网线损在线计算模型，当系统中某些节点电气数据不易获取时，也能学习其他节点电气数据与支路线损之间的关系，实现数据缺失情况下的线损计算。

3） 提出了基于RF 分类的配电网运行模式在线判断方法，针对配电网自动化水平较低导致不能及时感知网络拓扑结构变化的情况，通过RF 分类模型准确判断系统运行模式，为线损计算奠定基础。

1 随机森林分类与内核岭回归

1.1 内核岭回归

KRR 是引入非线性核方法的岭回归［17］。为便于描述，定义如下模型变量：状态矩阵X，即配电网状态，包括配网各节点负荷和DG 出力等；估计集合Z，即根据配电网状态得到的支路线损估计值；参数矩阵A，即KRR模型的参数。

设线性回归的模型为：

式中：B=(b1，b2，…，bn)为岭回归参数矩阵，b1，b2，…，bn为列向量，且=(b′n1，…，b′np)；X=(x1，x2，…，xn) 为配电网状态矩阵，x1，x2，…，xn为列向量，且=(x′n1，…，x′np)；n为岭回归参数矩阵及配电网状态矩阵的列数，与岭回归算法的参数数量有关；p为岭回归参数矩阵及配电网状态矩阵的行数，与配电网的规模有关。

设模型估计值Bguess为：

式中Loss(B)为损失函数。

为了避免因配电系统历史数据量不足导致矩阵不可逆的问题，引入正则化方法如式（3）所示。

式中：α为超参数矩阵；G(B)为正则化函数；arg min为最小变量函数。

KRR方法使数据在更高维度展开，从而实现配电网状态与支路线损之间关系的线性化［17-20］。在引入核方法的过程中，需要将KRR 参数矩阵B1内积化，由矩阵求逆引理［21］对B1化简可得：

式中：β为权重参数矩阵；βi为β中的第i个元素。

若加入新的配网状态矩阵x*，则相应的支路线损估计矩阵z*为新数据集与所有旧数据集内积的加权平均值。

1.2 随机森林分类

RF 将性能有限的多个分类回归树（classification and regression tree，CART）组合成一个“森林”，输出结果由每一个CART 的决策结果投票得到，相较于单个CART，RF 提高了分类的准确性［22］。CART 的分类选用基尼指数作为分割原则，对于数据集S中配电网状态的某一特征J，可将其划分为k个集合S1，S2，…Sk，其基尼指数GJ S可以写为：

式中GSk为数据集S第k个子集Sk的基尼指数。

一组CART 模型{t(X′，τi)，i= 1，2，…}组成一片RF。其中t(⋅)表示CART 模型；X′表示输入矩阵，包括配电系统中部分节点的电压以及部分支路的功率；τi表示第i棵树的参数。RF 分类的步骤如下。

1） 从数据集S中随机选取一个样本记为Xi；

2） 将选出的每一个样本Xi作为输入向量训练CART模型，促使决策树不断生长；

3） 重复步骤1）和2），直至N棵决策树生长完成，且N足够大；

4） 对未知数据分类时，模型输出结果由森林中N棵决策树投票决定，表示为：

式中：ρ为投票结果，即RF 模型的输出结果；Y为目标变量；Z(⋅)为示性函数；arg maxY为使示性函数取最大时的Y取值。

如图1所示为RF的形成过程。

2 基于RF与KRR的线损在线计算模型

基于RF 与KRR 的配电网线损在线计算将潮流计算转移至离线训练时进行，在线应用时使用训练完成的模型直接得到支路线损功率。

2.1 RF训练集与KRR训练集的建立

对于确定的配电系统，其典型的运行模式是确定的［20］，可通过配电网重构确定配电系统的典型运行模式。首先以配电网历史负荷以及对应时刻的DG 出力等配电网状态作为原始数据进行配电网重构；其次按照重构结果筛选出典型的运行拓扑结构，确定配电系统的典型运行模式；最后以配电网历史状态作为原始数据，按照不同模式分别进行潮流计算，选取配电系统中关键节点的电压与关键节点的支路功率作为运行模式的判据，并与其对应运行模式组成RF训练集。

将配电网历史负荷功率，以及对应时刻的DG出力等配电网状态作为原始数据，基于成熟的潮流计算方法获得每条支路的有功线损与无功线损，计算过程如式（8）—（11）所示，线损计算如式（12）所示。负荷功率、DG 电功率以及配电网支路线损功率即为KRR训练集中的一组数据。

式中：b(i，：)、b(：，j)、B分别为首节点为i的支路b、末节点为j的支路b、配电网支路集合；Rb和Xb分别为支路b的电阻与电抗。

式中：b(i，j)为首节点为i、末节点为j的支路b；Pb、Qb分别为流经支路b的有功功率和无功功率；Ib、Ui分别为支路b的电流与节点i的电压；、分别为节点i的注入有功功率和无功功率；与分别为系统根节点有功出力和无功出力；、分别为节点i上的DG以及负荷的有功功率与无功功率；分别为支路b的有功损耗与无功损耗功率。

对确定的配电系统，电网状态与支路线损存在较强的非线性对应关系，某些节点的状态虽然难以获取，但并不影响其他节点的状态与支路线损保持这种非线性对应关系，通过KRR 学习可获得节点状态与支路线损之间的联系，最终实现部分节点信息缺失条件下的配电网线损计算。

2.2 离线训练与在线应用过程

离线训练时，首先根据配电系统历史运行情况设置典型的运行模式；其次，在不同模式条件下进行潮流计算，建立包含系统节点负荷、DG 出力与线损功率的KRR 训练集以及包含系统部分节点电压、部分支路功率以及其对应运行模式的RF 训练集；最后，通过式（6）分解节点电压与支路功率的特征，基于RF 方法建立两者与配网运行模式的对应关系，基于KRR 方法寻找并确定负荷有功功率、负荷无功功率、DG有功出力、DG无功出力与支路有功损耗、支路无功损耗之间的非线性映射关系，并在此过程中通过式（4）确定KRR参数矩阵B1。

在线应用时，首先基于RF 分类模型通过式（7）由当前配网系统部分节点的电压和支路功率判断配电系统的运行模式；然后基于KRR 模型，根据当前配电系统的负荷有功功率、负荷无功功率、DG有功与无功出力，通过式（12）得到系统支路线损。

离线训练与在线应用过程如图2所示。

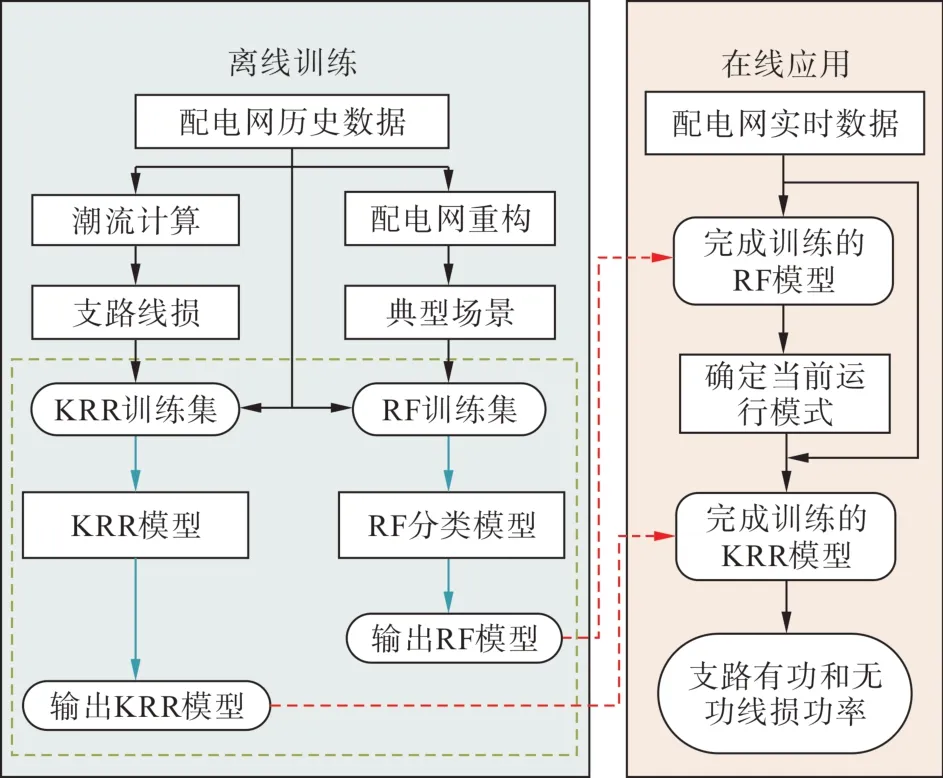
图2 KRR模型训练及应用流程图Fig. 2 Flowchart of KRR model training and application

3 算例分析

对图3 所示的IEEE 33 节点配电系统进行仿真，以验证本文所提方法和模型的有效性。该系统含2个分布式风力发电设备，2个分布式光伏发电设备，设备参数如表1 所示。配电系统的负荷数据来自文献［23］，DG 的出力数据来自文献［24］。通过JUPYTER Notebook 软件调用Keras 库训练KRR 模型，激活函数为sigmoid，学习率为0.001；通过JUPYTER Notebook 软件调用sklearn 库训练RF 模型，树的数量为10 000 棵，叶节点最小样本数为50。计算机配置为Win10 系统，CPU 为Intel Core i5-11300H，基准主频为3.10 GHz，GPU 为Intel（R） Iris（R） Xe Graphics，内存为16 GB。

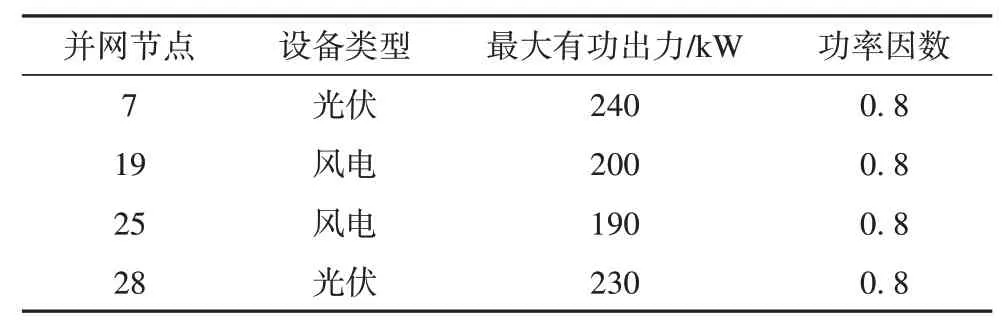
表1 分布式发电参数Tab. 1 Parameters of distributed generations

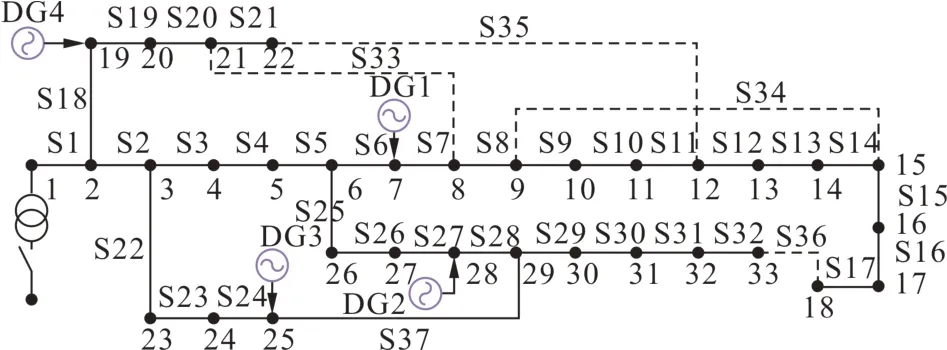
图3 IEEE 33节点系统图Fig. 3 Diagram of the IEEE 33-bus system

3.1 仿真环境设置

3.1.1 场景设置

为模拟配电网中节点实时电气量缺失的情况，本文参照山东某地区10 kV 配电系统数据缺失情况，按照线路首段量测设施较完备，线路末端量测手段较少的原则，分别设置3 个缺失节点数量不同的场景进行对比，如表2所示。

表2 不同场景数据缺失节点Tab. 2 Data missing nodes in different scenarios

3.1.2 评价指标

本文参考文献［12］中的评价指标，采用平均绝对百分误差（average absolute percentage error，MAPE）（记作EMAPE）和均方根误差（root mean square error，RMSE）（记作ERMSE）来评估模型预测结果的优劣，设可接受的预测误差为EMAPE<10%。

此外，通过平均绝对误差的标准差EσMAPE来描述预测结果误差的波动程度，并反映模型的鲁棒性。

式中：pi为第i个预测值的平均绝对误差；为n个预测值的平均绝对误差的平均值。

3.1.3 量测噪声

配电网实际运行过程中，受设备测量精度和通信干扰等因素的影响，获得的配电网运行数据不可避免地存在各种各样的误差。因此本文参考文献［16］，在量测数据中引入均值为0，协方差为10-2、10-3，权重为0.55和0.45的双峰高斯噪声。

3.2 算例结果及分析

3.2.1 运行模式划分及RF分类结果

通过配电网重构可以确定配电系统典型的运行模式。表3 是基于13 104 组历史数据的重构结果统计，由表3 可知，该系统的4 种典型运行模式能涵盖95.94%的历史运行情况，具有较好的代表性。现假设该配电系统只在此4 种模式下运行，以节点负荷与DG 出力情况作为确定不同运行模式的判据。

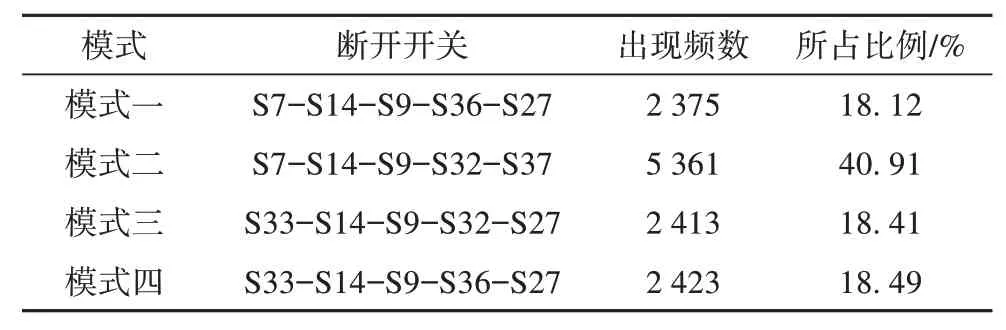
表3 重构结果统计Tab. 3 Reconstruction result statistics

选取配电系统中部分节点的电压以及部分支路的功率作为运行模式的判据。RF 训练时间为1 490.14 s，使用1 200 组数据进行测试，测试结果如表4 所示。由表4 可知，RF 分类法仅有2 次判断错误，其准确率为99.83%；测试时间为1.26 s，平均判断一次时间为1.05 ms，表明此方法能较为准确地判断配电网运行模式。

表4 分类测试结果Tab. 4 Classification test results

3.2.2 不同模式下的仿真结果

为了验证基于RF 与KRR 的配电网线损在线计算方法在不同运行模式下的实用性，本文在表5 中的多种模式下进行线损计算。KRR训练集中一组数据组成如下：各节点注入有功功率、各节点注入无功功率、各支路有功损耗功率、各支路无功损耗功率，并以1 MW 为基准值对训练集进行归一化处理。4 种模式KRR 的训练时间分别为421.70 s、413.07 s、426.46 s和409.68 s。

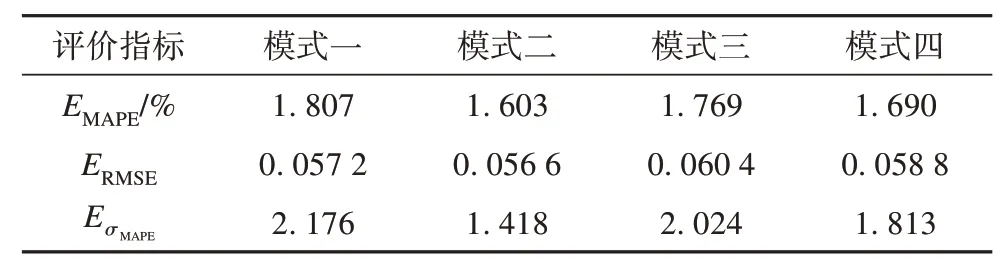
表5 不同模式评价指标对比Tab. 5 Comparison of evaluation indicators of different models

由表5 可知，各种模式的EMAPE在1.7%左右，ERMSE为0.06 左右，EσMAPE为2 左右。这表明基于KRR的配电网线损在线计算方法对于不同拓扑结构依然具有良好的适用性。

3.2.3 不同场景下的仿真结果

以3.2.1 节中的模式二为例分析不同场景下的线损计算结果。通过4 000 组数据构成的训练集对KRR模型完成训练后，使用1 000组数据进行测试，结果如图4和图5所示。得到1 000组预测值共用时0.761 5 s，平均预测一组的时间约为0.76 ms。

图4 32条支路有功损耗功率Fig. 4 Active power loss of 32 branches

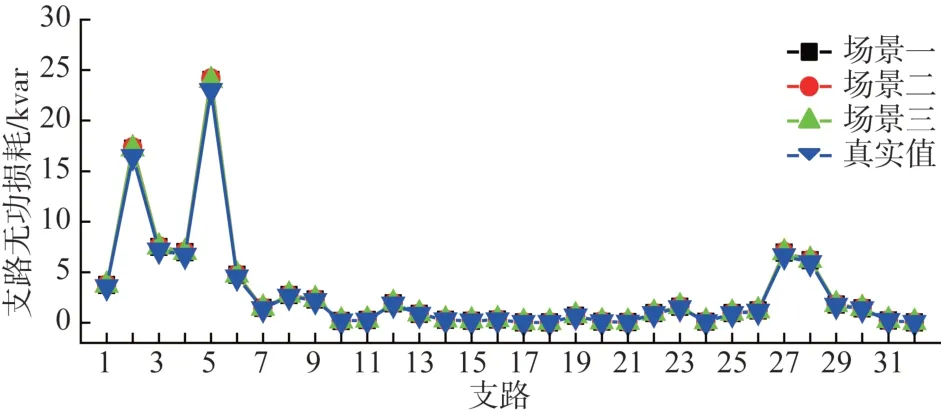
图5 32条支路无功损耗功率Fig. 5 Reactive power loss of 32 branches

图4和图5表明，3个场景中预测的功率损耗与真实值差别较小，预测结果曲线能够较好地跟踪真实功率损耗曲线。不同场景下预测结果的误差如表6所示。

表6 不同场景下的线损MAPE值Tab. 6 Line loss MAPE values in different scenarios %

由表6 可知，场景一中，支路有功损耗误差率平均值为1.602%，无功损耗误差率平均值为1.603%；场景二中，各支路有功损耗误差率平均值为1.991%，无功损耗误差率平均值为1.992%；场景三中，支路有功损耗误差率平均值为2.385%，无功损耗误差率平均值为2.384%。即相同场景中同一条支路的有功线损与无功线损误差差别不大，这是因为KRR 依据集合间的非线性关系进行预测，而相同支路中的有功与无功线损非线性关系类似。此外，在数据缺失率达30%的场景三下，线损估计误差平均值仍控制在2.5%以内，精度的降幅在可以接受的范围内。在场景三的基础上，继续增加缺失节点数量，去除节点14、19、22、23、30 节点数EMAPE为10.19%，ERMSE为0.46，EσMAPE为5.42，可知当数据缺失量过大时，线损计算鲁棒性变差，误差超过10%的可接受范围。

表7为不同场景下评价指标对比。由表7可知，场景一因为没有缺失节点数据，所以平均误差率最低，误差率最大值、平均绝对误差的标准差也最低，是3 个场景中预测效果最好的。场景二、三的平均误差率、平均绝对误差的标准差比场景一略大，这是因数据缺失而使预测精度降低的缘故，但数据缺失对精度的影响有限。场景三缺失数据量虽然多于场景二，但两者的平均误差率、平均绝对误差的标准差相差不大，这表明在数据缺失的情况下，KRR算法在线损计算应用中有较好的鲁棒性。

表7 不同场景评价指标对比Tab. 7 Comparison of evaluation indicators in different scenarios

3.2.3 不同方法下的仿真结果

为了比较KRR 与其他算法在配电网线损计算方面的优劣，本文将预测结果与文献［12］中的BP神经网络方法以及文献［13］中的LSTM、随机森林回归方法进行比较。由于上述文献没有考虑配电网节点数据缺失的情况，因此仅使用场景一的结果进行对比，各支路线损计算结果如图6和图7所示。

图6 不同方法下32条支路有功损耗对比Fig. 6 Comparison of active power loss of 32 branches of different methods

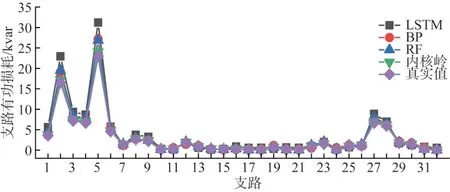
图7 不同方法下32条支路无功损耗对比Fig. 7 Comparison of reactive power loss of 32 branches of different methods

分别以EMAPE、ERMSE和EσMAPE作为预测精度对比指标，结果如表8所示。

表8 网损预测指标对比Tab. 8 Comparison of evaluation index of network loss prediction

从图6、图7、表8中对比可知，在不对量测数据进行处理的情况下，KRR的各评价指标都优于其他算法。这是因为KRR 的本质是寻找配电网状态与支路线损之间的非线性对应关系，使用配电网状态集合里的元素找到支路线损集合中与之对应的元素。而LSTM 适于对时间序列数据的预测，对于时间关联度较低的数据预测精度较低；RF 适于解决分类问题，在处理回归问题时易受噪声干扰而出现过饱和问题；BP 神经网络虽然结构简单、训练速度快，但是在处理较为复杂的非线性问题时往往效果不佳。通过对比可知，KRR在计算有源配电网线损功率中表现出较高的精度和较强的鲁棒性。

4 结论

本文提出了基于随机森林与内核岭回归的有源配电网线损在线计算模型，探究了在不同数量节点数据缺失情况下有源配电网线损计算的精度与鲁棒性。通过对IEEE 33 节点系统的仿真分析，得到以下结论。

1） 所提出的基于RF 分类的配电网运行模式判别模型对典型模式的判断准确率为99.83%，该方法能够比较准确地判断系统当前运行模式，为配电网线损在线计算奠定了基础。

2） 相较于LSTM 神经网络、RF 回归以及BP 神经网络等方法，本文提出的基于KRR 的配电网线损在线计算模型可以更深入地挖掘配网状态与支路线损间复杂的非线性映射关系，计算结果具有更高的精度和更好的鲁棒性。

3） 随着节点缺失数量的增多，基于KRR 的配电网线损在线计算模型的精度以及鲁棒性有所降低，但在数据缺失比例小于30%时，计算精度的降幅在可以接受的范围内。

本文提出的随机森林与内核岭回归的有源配电网线损功率在线计算模型虽然计算精度、鲁棒性较高，但所选的运行模式不能涵盖系统所有的历史运行状态，后续工作可以探究拓扑结构改变后的线损在线计算方法。