基于虚拟聚合和ACOPF 的电动汽车优化调度策略

武光华，李宏胜，汪洋，蔡博武，廖菲

（1. 国网河北省电力有限公司营销服务中心，石家庄 050000；2. 武汉大学电气与自动化学院，武汉 430072）

0 引言

近年来，随着能源危机和环境污染问题的不断加剧，开发利用新能源、减少温室气体排放已成为国家生态文明建设的重点。相较于传统燃油汽车，电动汽车（electric vehicle， EV）作为一种绿色交通工具得到快速发展，在减少二氧化碳排放、缓解能源危机等方面表现出强大的优势［1-4］。然而，当电力系统中的电动汽车达到一定规模后，可能会对电网的安全、稳定和经济运行造成一定程度的影响［5-7］。大量的负荷在某时间段聚集以及空间潮流分布不均匀现象的出现，严重时将发生阻塞等问题［7-9］。因此，对电动汽车群体进行必要的充电管理是提高用户利益和保证电网安全稳定运行的重要支撑。

目前国内外针对电动汽车参与配电网优化调度方面做了大量研究。其中文献［10］考虑负荷聚合商参与电力系统调度，构建基于双层优化的可削减负荷的调度模型；文献［11］基于负荷聚合商实现源荷互动，建立了配电网双层优化调度模型。但上述文献未考虑电动汽车负荷增大带来的电网阻塞问题。为此文献［12］将输电系统中节点边际电价的概念扩展到配电系统，提出了配电网节点边际电价（distribution locational marginal price， DLMP）概念，在文献［13-17］使用DLMP 来处理含分布式发电的配电系统中的阻塞。文献［18］考虑了聚合商设定的充放电价和车辆荷电状态对用户充放电响应度的影响，构建电动汽车优化调度策略。但上述文献均通过直流潮流模型求解，而忽略了网损和无功功率对配电网安全的影响。

另一方面，随着EV 渗透率的增大，需要优化的决策变量数量增加，不可避免地会导致较高的计算复杂度。文献［19］采用改进的基于非支配排序的多目标差分进化算法求解含风电及电动汽车电力系统动态经济调度问题；文献［20-21］基于交替方向乘子算法设计了主从结构分布式求解方案；文献［22-23］基于深度强化学习构建电动汽车充电导航策略。但以上研究均未从模型上减少决策变量来提升求解效率。

针对以上问题，本文提出了考虑单个荷电状态（state of charge，SOC）约束的电动汽车聚合方法，并基于虚拟聚合模型和交流最优潮流（AC optimal power flow，ACOPF）构建了电动汽车分散式调度策略。首先从分布式能源供应商、聚合商和电动汽车服务提供商等市场主体协同关系出发，设计了电动汽车灵活负荷参与配电网调度的框架；其次结合电动汽车站内充电时序关系建立电动汽车虚拟聚合模型，以通过聚合来减少目标函数中变量；然后考虑电动汽车负荷弹性，基于动态电价建立电动汽车群体参与配电网市场经济安全调度和站内电动汽车调度双层模型；最后，通过比较无聚集情况下得到的最优解，验证了所提方法的计算时间和最优性。

1 电动汽车调度整体框架

从电网运行的角度看，配电网阻塞不利于电力系统维持安全稳定运行状态；从用户的角度看，配电网阻塞会导致用户产生额外的阻塞成本，同时也会导致用户的用电计划不能得到满足；从电力市场的角度看，配电网阻塞会增加额外的市场力量，不利于市场正常交易［24］。因此，本文采取电力市场的手段去引导市场主体主动参与配电网调控，保证系统的安全和经济运行［25-26］。在未来的配电系统中，可能的市场参与者包括分布式能源供应商、聚合商和电动汽车服务提供商（包括家庭住宅区的充放电服务以及商用集中式充换电站服务）等。配电系统调度机构（ DSO）主要负责维护配电系统安全和经济运行，同时确保电力系统中的电能质量。在含有大量电动汽车灵活负荷的配电网中，由于EV集中充电可能导致电网出现阻塞。此时DSO需要根据用户需求特性及配电网的运行状态，对各个灵活负荷发出调整信号或指令，使系统维持安全稳定运行。

含电动汽车灵活负荷的配电系统市场结构如图1 所示，其中实线箭头表示电能传输过程，虚线箭头表示市场信号交换过程。在该市场结构中，电能由发电、输电系统经配电系统送到居民用户；DSO作为主要调度机构预测配电网次日的负荷需求，并通过电动汽车聚合商与电动汽车用户签订长期售电合同；聚合商以合同中的协议价格向电动汽车用户出售电能，并提交日前市场出清。

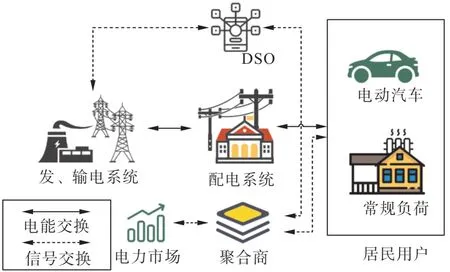
图1 含电动汽车灵活负荷的配电系统市场结构图Fig. 1 Distribution system market structure diagram with flexible loads for electric vehicles

电动汽车充电优化具体流程如图2 所示，DSO首先从聚合商或其自身的预测中获取EV 的需求数据，如能源需求和供应可用性，DSO还需要相关的配电网信息和预测的现货价格。假如电动汽车聚合商初定的用电计划会引起配电系统阻塞，此时DSO将会计算由于电动汽车等可控灵活负荷引起的阻塞价格发布给电动汽车聚合商；在接收到来自DSO的电价信息后，聚合商根据电价再次预测动态价格，并分别制定自己的最优充电计划；最后，聚合商向现货市场提交他们的能源计划市场出清。

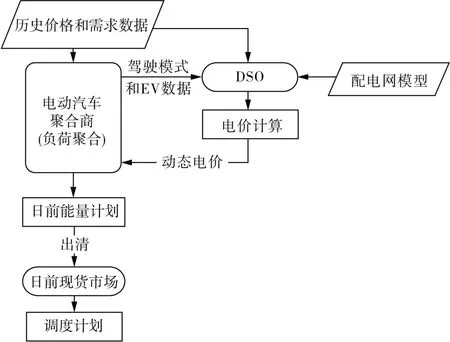
图2 配电网中电动汽车充电优化流程Fig. 2 Optimization process of EV charging in distribution network

2 电动汽车群体虚拟聚合

为了构建聚合模型，假设已知每一辆电动汽车的充电信息（包含充电起始时间、连接时长等），在电动汽车调度时，DSO 可获得电动汽车连接时间、电池容量、初始荷电状态（SOC）和充电需求作为输入。如图3所示，每个电动汽车用表示，其中n为车辆索引，用于区分连接在同一时段的车辆。即：

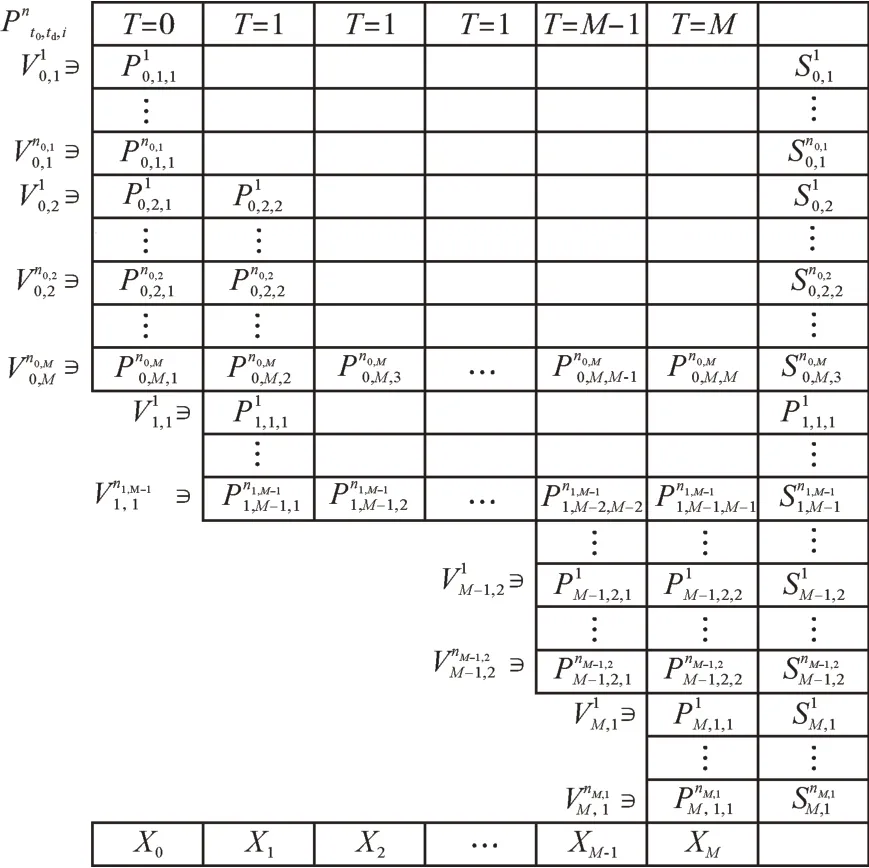
图3 站内电动汽车充电时序表Fig. 3 Charging sequence table of electric vehicles in the station

3 基于SOC-ACOPF 的电动汽车优化调度模型

3.1 配电网经济安全优化模型

电动汽车聚合商作为经济理性的市场参与者，在对电动汽车的充电行为进行优化调度时，大量电动汽车必然在电价低谷的时进行充电，进而导致负荷增加。当电动汽车容量达到一定程度时，可能会导致新的负荷高峰，严重时可能造成配电网阻塞，进而影响配电网的安全运行。DSO作为配电系统的运营中心，需要对系统阻塞情况做出判断，并给出解决阻塞问题的价格信号，达到缓解系统阻塞的效果。

3.1.1 目标函数

考虑到需求价格弹性，本文采用动态电价对电动汽车进行充电引导，其中包含与电动汽车负荷有关的部分，预测的动态电价由市场基础电价加上对需求预测的一个线性分量组成，如图4 所示。因此，在时段t的预测现货电价如式（9）所示。

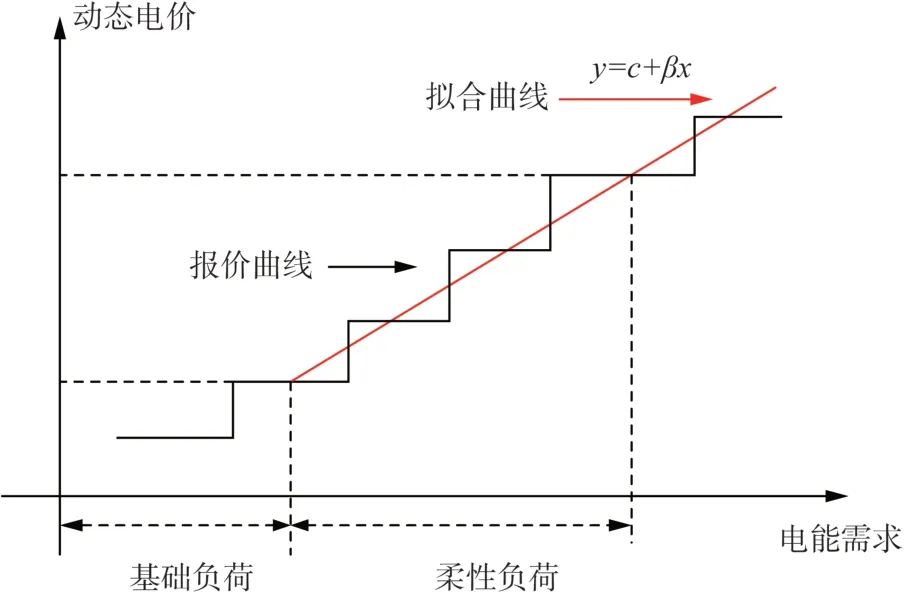
图4 考虑价格弹性的动态电价组成Fig. 4 Dynamic electricity price composition considering price elasticity

式中：EEV，t为电动汽车总负荷需求；yt为考虑了灵活负荷需求的系统电价；ct为系统基础电价，表示为满足系统中满足常规负荷需求的发电边际成本；βt为需求的价格敏感系数，电动汽车作为可控灵活负荷的一种典型负荷，当其需求改变时会对电价带来影响，该系数通常由系统的电动汽车调度情况决定。

目标函数为总配电系统中的总用电费用最小，包括电动汽车充电成本和常规负荷需求成本两部分，目标函数如式（10）所示，目标函数中第一项为电动汽车充电成本，第二项为常规负荷需求成本，在基础电价cj，t确定时常规负荷成本为常数。

式中：fDSO为总配电系统中的总用电费用；cj，t为基础电价；βj，t为价格敏感系数；Pcj，t为t时间段内位于节点j的充电站总的充电功率；PLj，t为配电网中t时段内节点j的常规负荷；J为配电网的负荷节点集合；T为时间段集合。

3.1.2 约束条件

1） 电力系统功率平衡约束

式中：PG，t为DSO 在t时段内的购电总量；Ploss，t为时间段t内的配电网总网损；PLk，t为配电网中t时段内节点k的常规负荷；L为配网的线路集合；rij为配电网中线路ij之间的电阻；iij，t为t时段内线路ij的电流；Ns为充电站集合。

2） 电网潮流约束

式中：Pij，t为t时段内线路ij传输的有功功率；Pkj，t为t时段内线路kj传输的有功功率；Qkj，t为t时段内线路kj传输的无功功率；u(j)为节点j的子节点集合；Qij，t为t时段内线路ij传输的无功功率；xij为线路ij的电抗；QLj，t为t时段内节点j的基础负荷无功功率；uj，t为t时段内节点j的电压。

3） 节点电压约束

式中：umin，j和umax，j分别为j节点电压的最低、最高安全边界。

4） 线路传输容量约束

式中Smax，ij为线路j的传输容量。

5） 充电站容量约束

式中Pcmax，j为充电站j的最大充电功率。

6） 充电需求等式约束

式中Qj为DSO 预测的充电站j全天的充电电量需求。

3.2 站内虚拟电动汽车调度模型

在DSO 发布动态电价至聚合商之后，聚合商需要综合考虑电动汽车的可调度情况和接收到的电价，并结合单台电动汽车SOC约束，调整电动汽车的充电计划，并通过用户充电成本最小为目标，来实现电动汽车对DSO 价格信号的自主响应，从而达到缓解配电网阻塞的效果。DSO制定日前电能计划完成市场出清，并得到动态电价（DLMP），作为充电站引导电动汽车调度的价格信号。

3.2.1 动态电价制定

充电站应以成本最小为目标，目标函数为式（21），约束条件同式（11）—（20）。

式中fCS为配电网中所有充电站的购电费用总和。

由于式（11）和式（18）含有二次变量使得模型非凸，将其线性化可得式（22）—（23）。

式中：DF0，t为t时段内平衡节点的有功功率传输灵敏系数；DFj，t为t时间段内节点j的有功功率传输灵敏系数；J'为配电网中的所有节点集合；为平衡节点的功率传输分布因子；为节点j的功率传输分布因子；Pmax，ij为线路ij的有功功率传输能力。

通过对偶原理，可得式（21）—（23）对应的拉格朗日函数如式（24）所示。

式中：G 为拉格朗日函数；λt和μij，t分别为式（22）和式（23）的对偶变量。

动态电价由三部分组成，如式（25）所示，其中第一项为基础电价，第二项为网损边际电价，第三项为阻塞电价。

式中πj，t为t时段内节点j的动态电价。

3.2.2 虚拟电动汽车调度

电动汽车群体能够根据价格信号分散式优化其电能计划，故站内虚拟电动汽车调度优化目标如下：

式中fVEV为虚拟电动汽车充电费用总和。

约束条件如下。

1） 充电需求约束

式中：T'/T为每个小时所包含的调度时间段集合；Nsj为充电站j预测的站内车辆；pn，t为t时段第n辆EV的充电需求。

2） SOC约束

3） 充电功率约束

式中pmin和pmax分别为电动汽车最小、最大充电功率。

4 模型转换与求解

4.1 二阶锥松弛线性化

在配电网经济安全优化模型中，由于潮流方程的非凸性，原问题难以获得全局最优解，且模型中式（10）—（20）构成了一个非线性规划问题。通过二阶锥松弛（second order cone， SOC）能够将原问题转化为凸优化问题以快速求解，则原问题为二阶锥直流最优潮流模型（SOC-ACOPF）。

式中Uj，t、Iij，t分别为替换后的变量。

采用上式对原变量进行替换，转换为以下形式。

4.2 模型求解流程

本文提出了电动汽车聚集方法和多阶段优化方法来解决充放电调度问题。首先，将单个电动汽车聚合成虚拟电动汽车，即电动汽车聚合集群模型，以减少目标函数中变量的数量，进而减少计算量。其次，转向多阶段优化。优化的第一阶段建立配电网经济安全优化模型（称为阶段A），考虑电网的经济安全约束，得到每个充电站的最优功率计划和动态电价。第二阶段（阶段B）在考虑单个电动汽车荷电状态约束的同时，将虚拟电动汽车充放电能量分配给单个电动汽车。如果由于优化的结果不满足阶段A 的约束，则将给定的虚拟电动汽车解送回A 阶段。阶段A 更新虚拟电动汽车的约束条件。具体求解流程如图5所示。

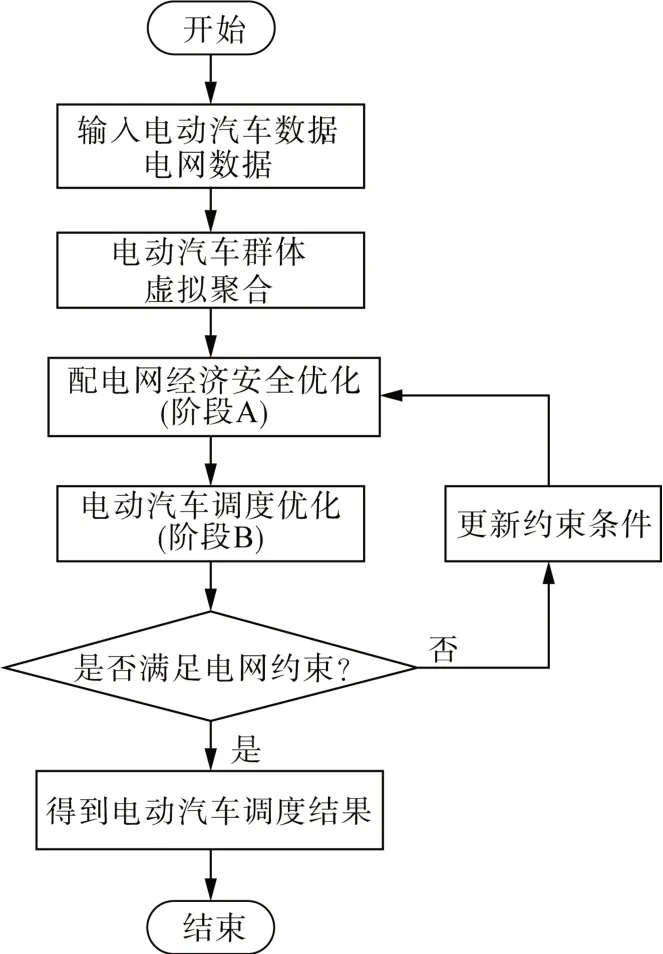
图5 模型求解流程Fig. 5 Model solving process

5 算例分析

5.1 参数设置

本文的仿真采用IEEE 33 节点标准配电系统，并对其负荷情况进行修改。配电网的拓扑图与聚合商的位置如图6所示，该系统一共包含33个节点和32 条支路，其中0 节点为平衡节点，一共包含6 个充电站，分别位于1、2、13、21、23、28 节点处，线路容量的上限为9 000 kW。此时，由于大量电动汽车负荷的接入，首端线路最容易发生配电网阻塞，因此本文选择对线路1-2 的负载情况进行分析。

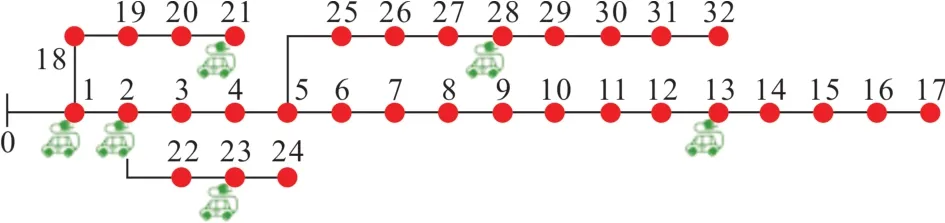
图6 IEEE 33节点配电系统Fig. 6 IEEE 33 power distribution system

假设配电系统内共有3 200 位居民用户，除平衡节点0之外，其余每个充电站节点均包含40辆电动汽车。本文假设不同节点之间的常规负荷和电动汽车的用电特性及参数均相同，而同一个负荷节点的常规负荷和电动汽车的用电特性和参数各不相同。其中每条线路的常规负荷如图7 所示，01：00—06：00 期间由于大部分居民均处于睡眠时段，因此负荷较低；而在19：00 左右时段由于大部分居民在家中导致常规负荷增大。电动汽车参数信息如表1 所示，电动汽车可控率可由电动汽车驾驶模式调查［20］中获得，给定仿真时限T=24 h，并以1 h 为时段单位进行算例分析。电动汽车的充电信息取自华北地区某一充电站1 月某日实际数据，基础电价如图8所示。

表1 电动汽车参数信息Tab. 1 Parameter information electric vehicle

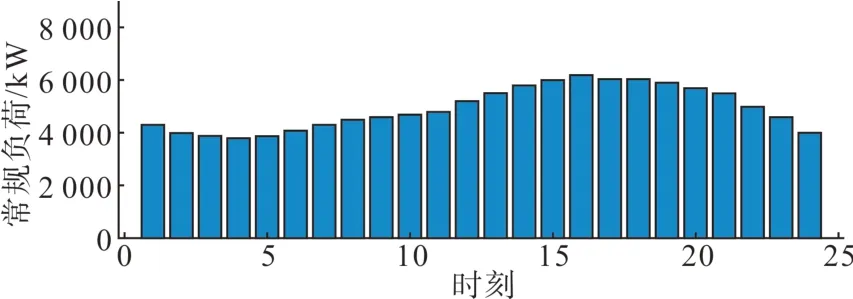
图7 常规负荷曲线Fig. 7 Conventional load curve

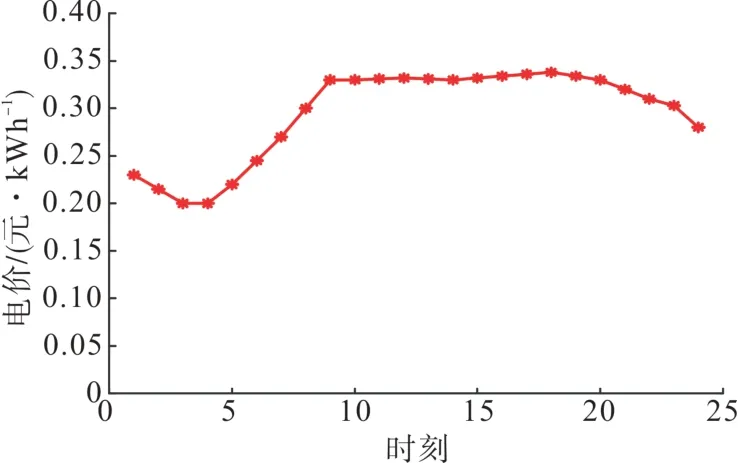
图8 基础电价Fig. 8 Base price

5.2 仿真结果

5.2.1 阻塞管理效果对比分析

为了清楚地突出本文提出的调度策略的效果进行了两种情况对比分析。

场景一：系统未采用动态电价机制；

场景二：系统中采用动态电价机制对电动汽车充电进行有序引导。

采用动态电价前后的线路1-2 负荷情况如图9所示。由图9（a）可以看出，在03：00 和04：00 时线路1-2 由于电动汽车集中充电使得负荷超过了线路容量限制，即此时线路1-2 发生了配电网阻塞。而由图9（b）可以看出，经过调整之后，原04：00 和05：00 内线路负荷转移至02：00 内，即电动汽车充电负荷分布在电价较低的几个小时内，而不是在1 h 内对所有的电动汽车负载进行充电。证明了动态电价能准确反映阻塞线路的微增率，并通过电价的形式对电动汽车充电进行有序引导，以达到规避系统阻塞的效果。

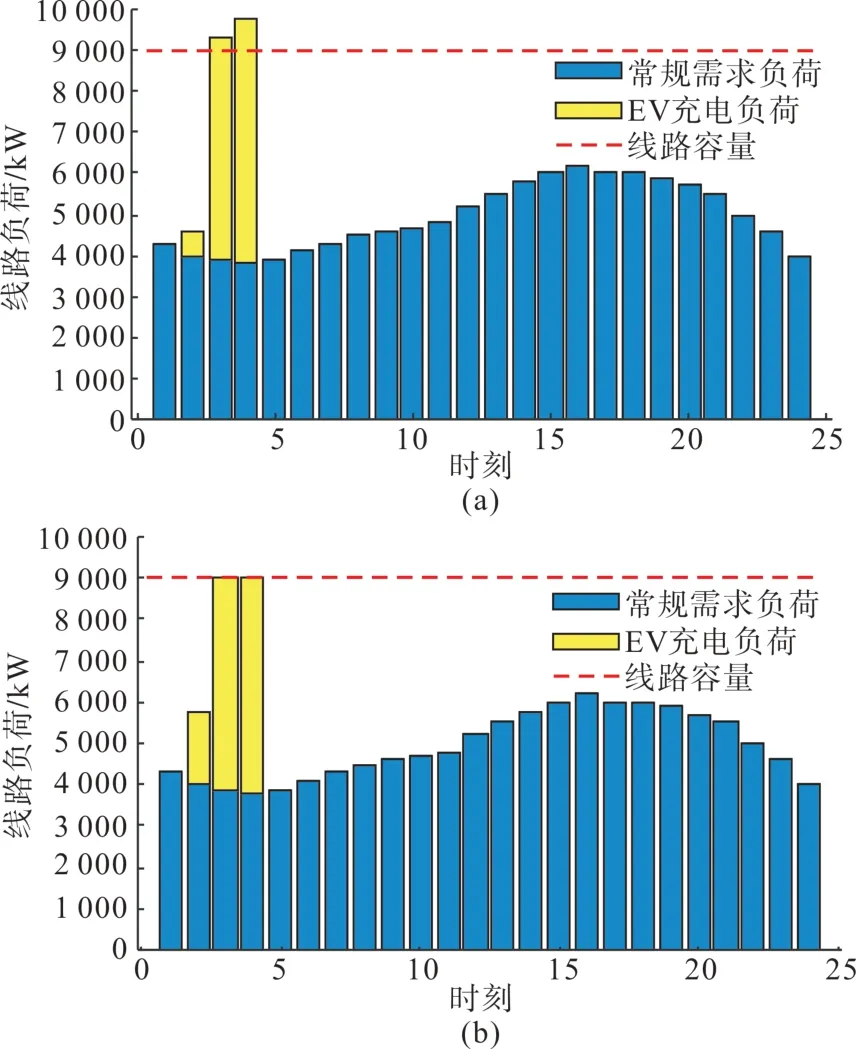
图9 采用动态电价机制前后线路1-2负荷Fig. 9 Line 1-2 loads before and after using dynamic electricity price mechanism

5.2.2 最优潮流策略分析

表2 比较了无序充电模式与两种最优潮流模式下配电网的各项指标。相比于无序充电模式，在最优潮流模式下DSO 的购电费用、峰谷差和网损均有所降低，同时无序充电会导致配电网部分节点电压跌落。DC-OPF 模型由于未考虑网损，因此网损为0，但会导致峰谷差增大，而二阶锥直流最优潮流模型（SOC-ACOPF）保证配电网的电压质量在安全运行范围内。可见，本文所提的SOC-ACOPF 策略有助于配电网安全经济运行。

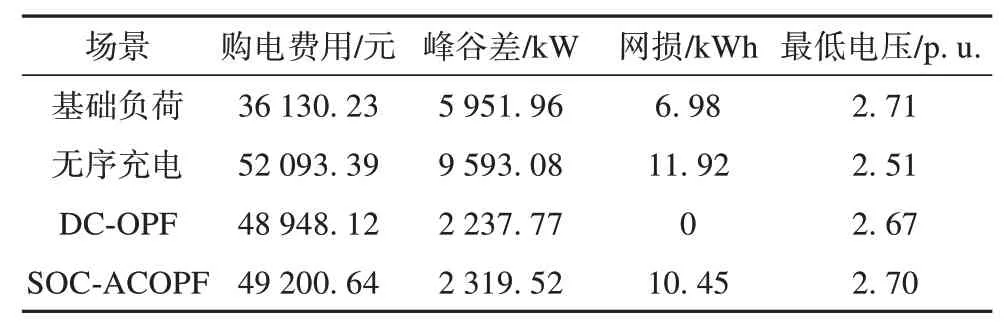
表2 交流最优潮流优化结果Tab. 2 Result of SOC-ACOPF

为了证明本文提出的求解策略的有效性，对DSO模型和聚合商模型的电动汽车优化调度结果进行了对比分析，负荷计划对比如图10所示。

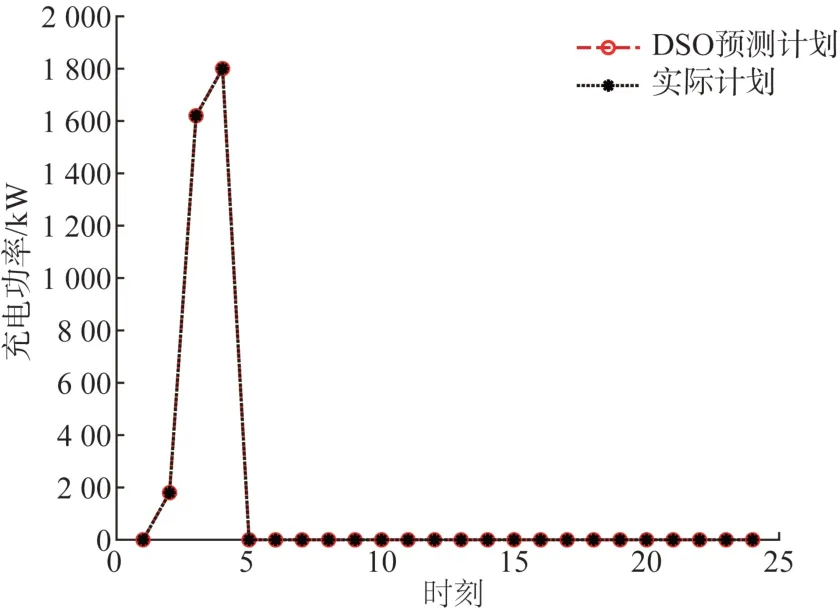
图10 负荷计划对比Fig. 10 Comparison of load plan

通过图10 可以看出，两种情景之下的DSO 模型和聚合商模型的调度结果完全相同，即本文提出的动态电价能准确反映阻塞线路微增率。与证明过程结合，进一步证明了本文提出的求解策略的有效性，另一方面也证明了本文提出的节点边际电价制定模型中，DSO总是能准确地预测聚合商的负荷计划这一结论的正确性。

5.2.3 调度结果经济性对比分析

将系统中基础电价与动态电价进行对比，如图11 所示，在线路1-2 发生阻塞的时段，即03：00 和04：00 时，对应的动态电价会比基础电价相对高，这是由于该时段系统出现了阻塞，因此市场运营商需要通过抬高电价的方式来引导电动汽车用户选择其他的充电时段以减小该时段的负荷。而边际电价与基础电价相差的数值为线路的阻塞成本，反映了该节点的负荷微增率。

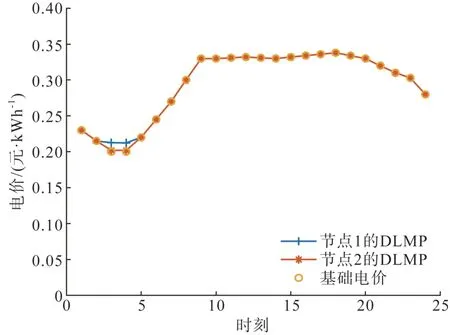
图11 基础电价与动态电价Fig. 11 Base price and dynamic price

通过分析，充电站会在动态电价的引导下结合单个电动汽车SOC 以约束修改EV 充电计划，使得线路1-2 的最大负载率显著降低。同时，在动态电价的引导下，电动汽车的充电时间也会有所改变，避免了大规模的集中充电。相应地动态电价中的阻塞成本导致聚合商的总购电成本提高，即用户的总充电成本提高，统计结果如表3 所示。通过上述分析可以得出，本文所提出的方法可以通过电价机制引导电动汽车有序充电，进而有效避免线路阻塞，保证电力系统的安全运行。

表3 线路1-2最大负载率和成本比较Tab. 3 Line 1-2 maximum load rate and cost comparison

5.2.4 算法求解效率对比分析

为验证本文提出的SOC-ACOPF 的准确性，本文对比了以下几种最优潮流计算方法。

1） DC-OPF（direct current optimal power flow），直流潮流计算；

2） ACOPF，源于MATPOWER 6.0的交流最优潮流计算程序；

3） L-ACOPF，线性化最优潮流计算［25］；SOCACOPF；

4） 本文的求解算法。

由于日前调度结果通常在报价结束的几个小时后才发布，因此日前调度结果主要关注准确性及收敛稳定性。计算结果如表4 所示，可以看到，由于DC-OPF 不考虑网损和无功损耗，计算时间最短，但存在较大的误差。此外，由于L-ACOPF 计算速度相对于传统ACOPF 快，但因其网损是基于灵敏度求解，会出现损耗为负值的情况导致误差相对偏高。而本文计及虚拟聚合的SOC-ACOPF 方法能保证计算精度的同时加快求解速率，相对普通线性最优潮流及传统最优潮流方法在可行性方面有一定优势。

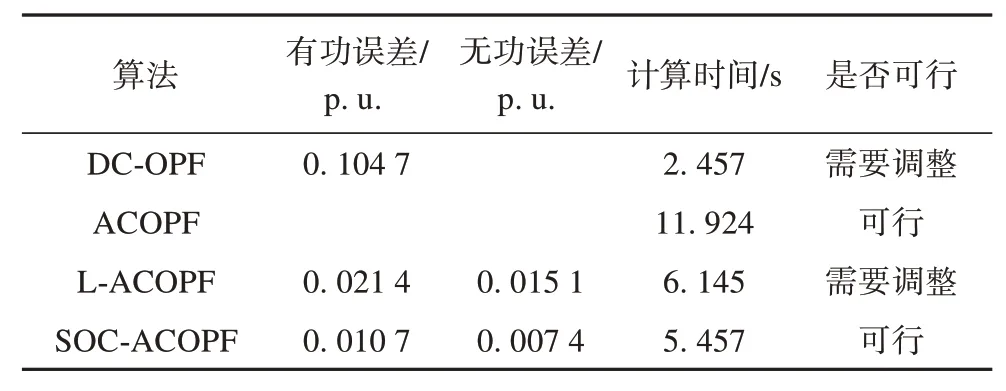
表4 最优潮流计算对比结果Tab. 4 Optimal tide calculation comparison results

图12 为随着电动汽车数量增加，获取电动汽车调度计划的计算时间。最优调度考虑所有单个电动汽车的SOC约束，但计算时间随着电动汽车数量的增加呈指数增长。另一方面，基于该方法的600辆电动汽车的计算时间是传统方法的51%。随着协同电动汽车数量的增加，传统方法的计算时间呈指数增长，本文所提出的方法具有更大的优势。

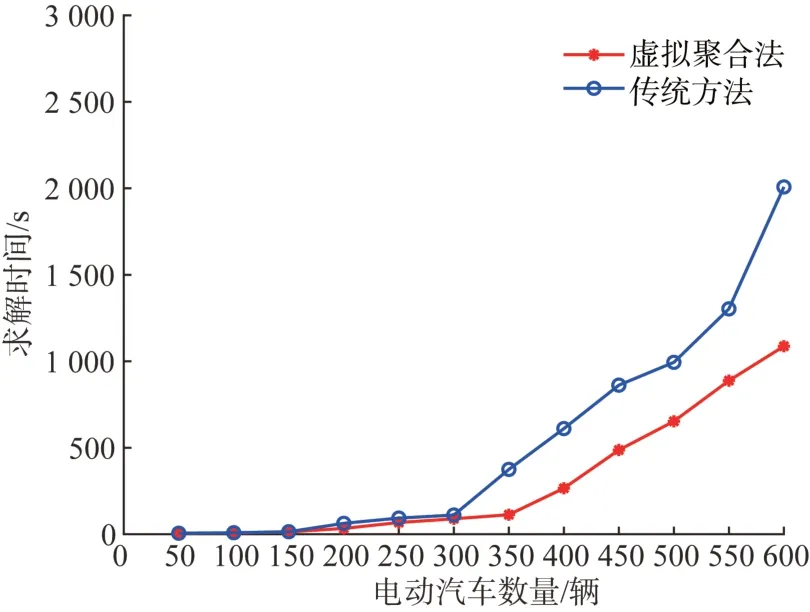
图12 常规方法和虚拟聚合法的求解时间Fig. 12 The solution times of conventional method and virtual polymerization method

6 结论

本文综合考虑动态电价和市场机制，设计了电动汽车灵活负荷参与配电网调度阻塞管理模型，通过算例分析，比较了不同机制下DSO 的收益以及常规方法和虚拟聚合法的求解时间。主要结论如下。

1） 基于ACOPF 策略能够降低DSO 的购电费用，并能降低配电网的网损和峰谷差，提高配电网的电压质量。

2） 动态电价中包含了分时电价、网损均摊费用以及阻塞费用，能够作为公平的价格信号引导电动汽车有序充电，在保证配电网安全经济运行的同时能够降低充电成本。

3） 电动汽车虚拟聚合提高求解效率，基于该方法的600 辆电动汽车的计算时间是传统方法的51%。随着协同电动汽车数量的增加，该方法具有更大的优势。

本文的下一步研究方向包括：考虑不同类型电动汽车的行为，并通过节点边际电价策略衡量功率对降低电网网损、提高电网电压质量以及解决线路阻塞问题的贡献。