挖掘机铲斗电液伺服改进PSO-PID参数整定位置控制

张晓婷，李徳镇，梁仁旺，贺婷婷

（1.重庆水利电力职业技术学院建筑工程学院，重庆 永川 402160；2.中国水电基础局有限公司，天津 武清 301700；3.太原理工大学建筑与土木工程学院，山西 太原 030024）

1 引言

为实现挖掘机设备的自动控制功能，需保证对其运动机构位置的精确控制[1-3]。选择21t挖掘机作为测试对象，考虑到挖掘机运行过程中电液伺服系统会形成死区与摩擦作用，对铲斗进行位置控制时也表现出了明显非线性特征[4-5]。文献[6]运用智能PID控制技术，有效克服了电液比例压力控制的缺陷；文献[7]构建了挖掘机电液比例系统的非线性模型，并对挖掘机电液控制系统进行了优化，建立了相应的分段模型。文献[8]设计了一种包含干扰算子的粒子群优化算法，实现粒子群算法稳定性的显著提升；文献[9]在PSO算法中加入最优粒子分析方法，之后利用改进优化的粒子群算法实现对非线性PID系统的控制，显著改善算法精度与实时性。

根据挖掘机电液伺服系统的运行性能来达到调控挖掘机铲斗位置的功能[10]，由于采用传统PID整定方法并不能获得优异控制效果，因此采用遗传算法与交叉算子、标准PSO算法进行PID整定，最后对其进行了仿真验证。

2 铲斗电液伺服系统

2.1 电液比例系统

挖掘机铲斗电液伺服控制系统的各个组成部分，包含了多路阀、运行控制机构、液压缸、减压阀、放大器、位移探测器多个结构[11]，如图1所示。

图1 电液比例系统框图Fig.1 Block Diagram of Electro-Hydraulic Proportional System

2.2 电液比例阀传递函数

当控制器形成电压信号后，在比例放大器中完成转换过程并造成压力作用，之后驱动多路阀形成阀芯位移，得到以下的传递函数[12]，如式（1）所示。

式中：Kp—比例减压阀增益；K—比例放大器增益；Tv—间常数。

2.3 阀控非对称缸传递函数

挖掘机多路阀-油缸系统属于一种对称阀控-非对称液压缸结构，以下为液压缸伸出工况下的传递函数计算式：

式中：Kq—先导阀的流量增益；ξn—液压缸的阻尼比；ωn—液压缸的固有频率；A1—无杆腔的截面积。

3 改进PSO-PID参数整定算法

3.1 标准PSO算法

粒子群优化算法属于一类智能控制算法，利用群体信息共享的方式获得群体智能[13]，并对优化搜索过程提供指导，以下为具体优化规则：

假定N维搜索空间内包含了m个粒子，将第i个粒子位置向量表示成xi，对应的速度向量为v，以Pbest表示第i个粒子最好位置，以Gbest表示粒子群最优位置，按照以上规则，采用上式对第i个粒子迭代t+1次后位置与速度进行更新。

以适应度函数完成算法优化，对各粒子当前位置适应度计算结果实施排序，从中筛选出较差适应度的50%粒子，再以另外50%粒子对其速度与位置进行替换，同时保持恒定的历史最优位置。经过选择后，粒子群会对最优空间先进行搜索分析，并且依然会受到个体最佳位置的干扰[14]。按照随机方式对粒子进行两两杂交处理，同时以用户自定义交叉概率生成后代粒子并对父代粒子进行替代，由此控制恒定的粒子数量，最后池内所有粒子都完成交叉过程。通过加权计算的方式获得后代粒子位置：

式中：rc—交叉概率；child1（xN）—后代粒子位置；child1（v）—后代粒子速度；parent1（xN）、parent2（xN）、parent1（v）、parent2（v）依次对应父代粒子位置与速度矢量。

3.2 惯性权重系数调整

对于标准粒子群算法，可以通过设置惯性权重系数来实现收敛速度，当惯性权重系数ω较大时，能够实现全局搜索并获得较快收敛速度，当ω较小时，可以实现局部搜索的功能，但只能以较慢的速度收敛，这使得算法最初阶段获得了较大的惯性权重，之后转变为较小的惯性权重系数[15]。

式中：ωmax、ωmin—最大与最小惯性权重系数；Tmax—最大迭代次数；t—迭代的次数；k—非线性控制因子。

4 仿真分析

选择MATLAB软件编写算法流程[16]，同时以simulink构建仿真模型并完成仿真测试。仿真模型的各项参数，如表1所示。以下为挖掘机电液伺服系统开环传递函数：

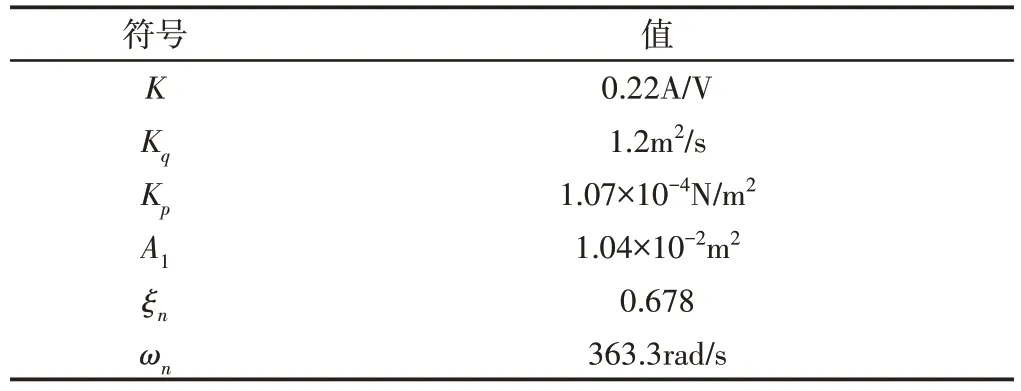
表1 仿真模型参数Tab.1 Simulation Model Parameters

挖掘机铲斗电液伺服系统模型，如图2所示。再利用理论计算方法对其进行了验证。整定参数设定，如表2所示。

表2 整定参数设定Tab.2 Setting of Setting Parameters

图2 仿真模型Fig.2 Simulation Model

进行铲斗控制测试时，将y=0.5m作为单位阶跃信号结果，如图3所示。考虑到优化过程存在随机性，分别以三种算法进行10次测试并选择最优值，分别以不同整定方法获得上升时间、调整时间以及ITAE参数，测试结果，如表3所示。可以发现，所有算法都没有发生超调的现象，1s时也未产生滞后的情况，形成了相近的曲线变化特征。采用改进PSO算法整定时达到了最快的系统响应速度，表现出了优异的动态特性，控制精度也得到了显著提升。时间介于（1～1.5）s之间时，比例系数发挥主导作用，此时采用三种算法得到了基本一致的位移曲线。对各算法进行比较可知，改进PSO算法达到了其它两种算法更短的上升时间与调整时间，同时ITAE值也更小，经过0.528s后进入稳定状态。

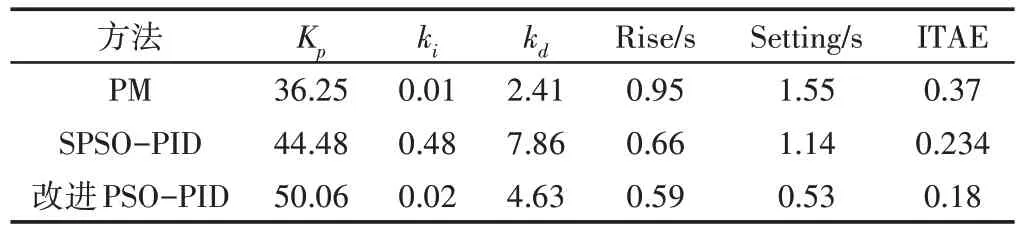
表3 整定值统计Tab.3 Settings Statistics

图3 阶跃响应结果Fig.3 Step Response Results

按照图4的方法对系统进行动态性能测试。输入频率等于0.5Hz与振幅等于0.5m的正弦波信号，能够对油缸期望位移形成快速响应，形成了同样的位移变化特征，采用三种方法进行整定得到的位移曲线都出现了延迟的现象，其中，以改进PSO算法进行整定时获得了0.13s的最短延迟时间。

图4 正弦跟踪响应结果Fig.4 Result of Sinusoidal Tracking Response

形成了正弦变化的误差曲线，与输入信号频率一致，结果，如图5 所示。以改进PSO 整定获得了最小误差，误差最大值为76mm，处于允许误差范围之内。上述结果表明，改进PSO算法获得了优异的综合性能指标。

图5 跟踪误差Fig.5 Tracking Error

5 实验

为分别验证标准粒子群方法、相位裕度法、改进粒子群算法的整定性能，本实验选择某21t自动化挖掘机实施验证，具体，如图6所示。

图6 实验照片Fig.6 Experimental Photos

利用LM专用软件设计控制系统，结合设计测试条件与挖掘机的自身运行参数设置了目标轨迹。从图6中可以看到，参数输入以及表示运动轨迹的监控界面工作期间铲斗位置和目标轨迹之间的误差，利用CAN-BUS 总线跟计算机之间构建通信渠道。控制挖掘机处于空载状态下进行平地动作的仿真测试，使目标轨迹与地面之间相距40cm，铲斗速度接近0.2m/s，测试得到的结果，如图7所示。

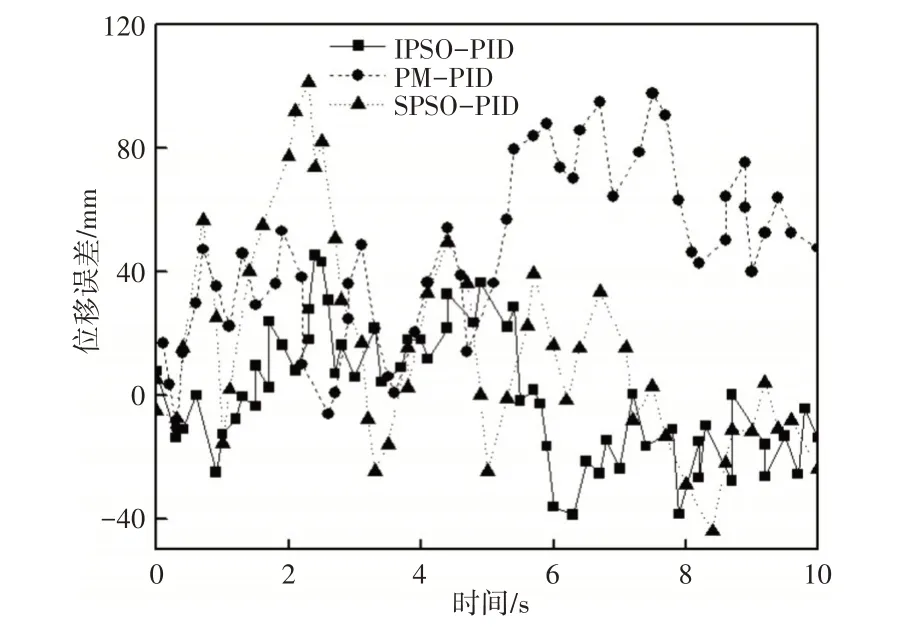
图7 期望与实际轨迹位置误差曲线Fig.7 Expected and Actual Trajectory Position Error Curve

图7给出了分别以三种算法测试铲斗运动位置和目标位置之间的差值，其中，PM 算法获得了100mm 的最大误差，以SPSO与改进PSO智能算法进行处理后可以获得更小的误差，尤其是以改进PSO智能算法进行处理时获得了最明显的效果，最大误差只有40mm。

6 结论

为增强粒子群算法搜索性能，综合运用遗传算法与交叉算子来实现对标准粒子群的优化，显著改善PID控制器性能，根据推导得到的铲斗系统模型进一步开展仿真分析。分别以三种优化算法计算优化结果，再将其输入自动化挖掘机程序中，完成各参数修改后，再对平地控制过程进行模拟测试。根据实验测试可知改进PSO算法具备明显优越性。