四边形自适应网格的局部加密算法

王志明,肖源明,李留洋,王 波,刘心志

(1.南京理工大学,江苏 南京 210094;2.南京大学, 江苏 南京 210008;3.中国船舶及海洋工程设计研究院,上海 200011;4.故宫博物院,北京 100009)

0 引言

在工程结构计算领域,为了精确描述结构特征,通常采用加密的网格化模型进行仿真运算,由于模型包含的网格数量可高达上百万个,但是如果直接对整个计算区域进行网格加密,硬件资源需求较高、计算时间相对较长,会造成巨大的资源浪费。局部网格加密就是在部分降低计算时间和资源使用要求的基础上,提高计算精度的网格处理方法,相较于整体均匀网格化处理,有着巨大的优势。使用该方法可以很好地解决计算精度与计算时间之间的矛盾,具体方法表现为在粗网格区域演化时间步较长,计算量较小,可以较快获得运算场的大致结构;在细网格区域则可以捕捉变化剧烈区域更加准确的数值变化,因此可以兼顾计算精度与效率,自适应地解决这类问题。工程上称这种可合理地分配计算资源的数值方法为自适应有限元方法。在实际工程中,人们需要的只是获得局部区域结构的精确解,故提出一种四边形网格的局部加密策略,在减少计算量和计算时间的同时,快速获得所需局部的精确计算结果。

1 局部加密方法及相关概念

四边形自适应局部加密算法的具体步骤如下:首先进行网格生成,然后使用有限元方法对变分问题进行数值求解,得到数值结果后进行误差分析,根据结果标记误差超出允许阈值的区域,对这些区域进行网格加密,然后针对不同区域实施针对性的加密,再次进行求解,最后经过多次循环直至得到满足要求的结果。本研究基于给定的标记区域进行加密,主要研究网格调整过程中的加密策略,简化了初始网格的生成以及边界网格的处理,假设初始的四边形网格划分算法已生成协调的计算网格[1-4],并对相关概念进行了详细说明和定义。

1.1 单元及网格剖分

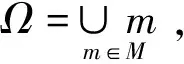
上述定义的单元m∈M,包含其边界。这里的划分区域所使用的单元主要是一般的四边形,允许网格单元中出现悬点。所谓悬点v,即v作为某个单元m1∈M的顶点,却位于另一单元m2∈M边的内部[5]。而实验需要考虑的正规网格(或称协调网格)是不存在悬点的。

1.2 正规网格

令M为Ω上的网格,Γ:=∂Ω为Ω的边界,如果:

(1)对于所有的m∈M,m∩Γ若非空,则为m的一个顶点或m的一条整边;

(2)对于所有的m1≠m2∈M,m1∩m2若非空,则为他们的一个共同顶点或一条共同边。

若同时满足以上两个条件则称网格M为正规的,根据这一定义判断,本文中的正规网格皆不存在悬点[6-7]。

2 四边形网格的加密策略

2.1 消除悬点

由于加密策略是基于正规网格进行的,因此,加密后的网格也应保证正规性。此外,加密策略中还需要注意网格单元的稳定性,即单元角度不会随着加密过程变得越来越小。研究过程中,如图1所示的单元加密模板,其中数字表示单元需要加密的次数。假设将单元的边三等分为9个单元作为一次基本加密操作。然而,如果不进行额外处理,将会导致单元中出现悬点,从而破坏网格正规性。因此,需要设计相应的模板,在加密单元的邻域中引入过渡单元,以消除悬点。

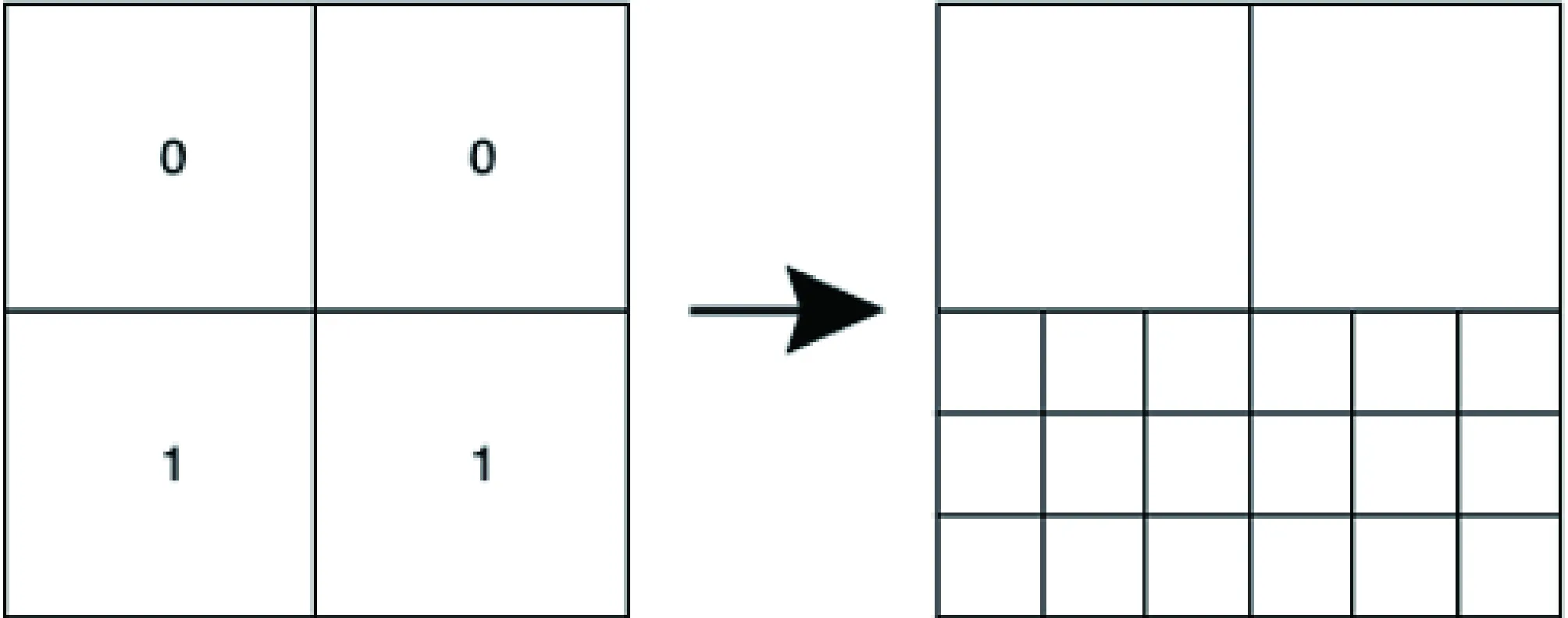
图1 网格中单元的加密

2.2 加密模板a

通过处理非加密单元可以消除悬点,如图2所示是一种加密模板方法,该模板具有网格正规性。但是,当将图中两个单元的加密次数设为2时,将会产生新的问题。如图3所示,使用该加密模板会导致内角角度较小的四边形单元的出现,而随着加密次数增多,这种角度变小的趋势将会持续。过于畸形的单元出现会导致后续计算的精度大大降低。

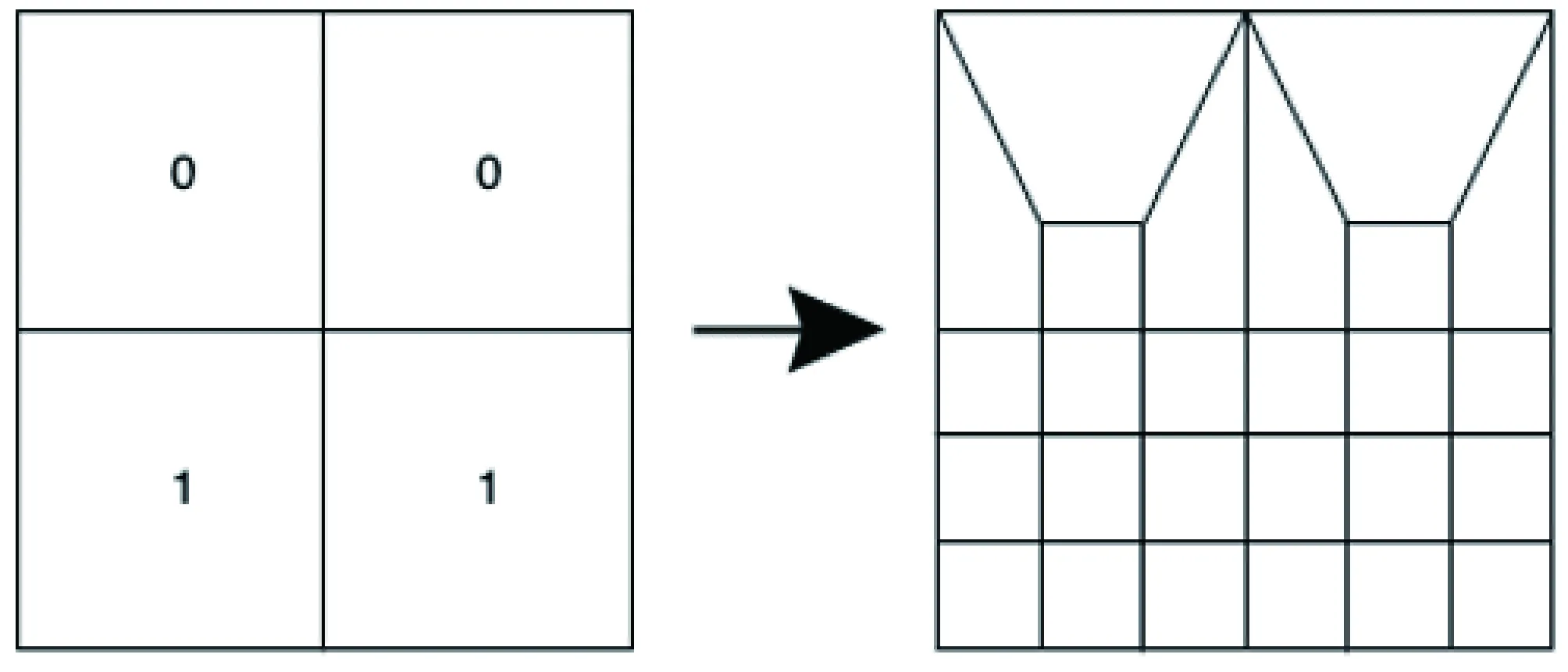
图2 通过处理非加密单元来消除悬点

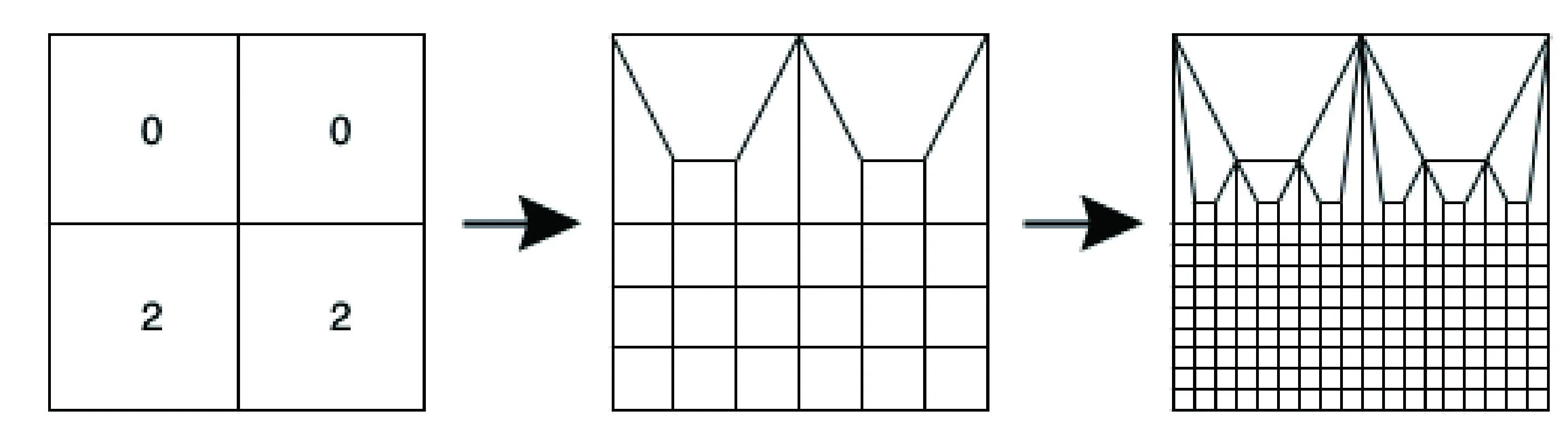
图3 二次加密出现四边形内角最小值变小的情况

2.3 加密模板b

若使用如图4所示的加密模板,加密过程中产生的四边形单元内角的最小值将不会受加密次数的影响。以一个单元数较多的网格为例,如图5所示,左侧为原始网格(区域中有一个洞,灰色为标记加密单元),右侧为加密一次后的网格,其中除标记单元需要被三等分外,其邻居单元也需作部分加密。

图4 二次加密后四边形内角角度最小值不发生变化的情况

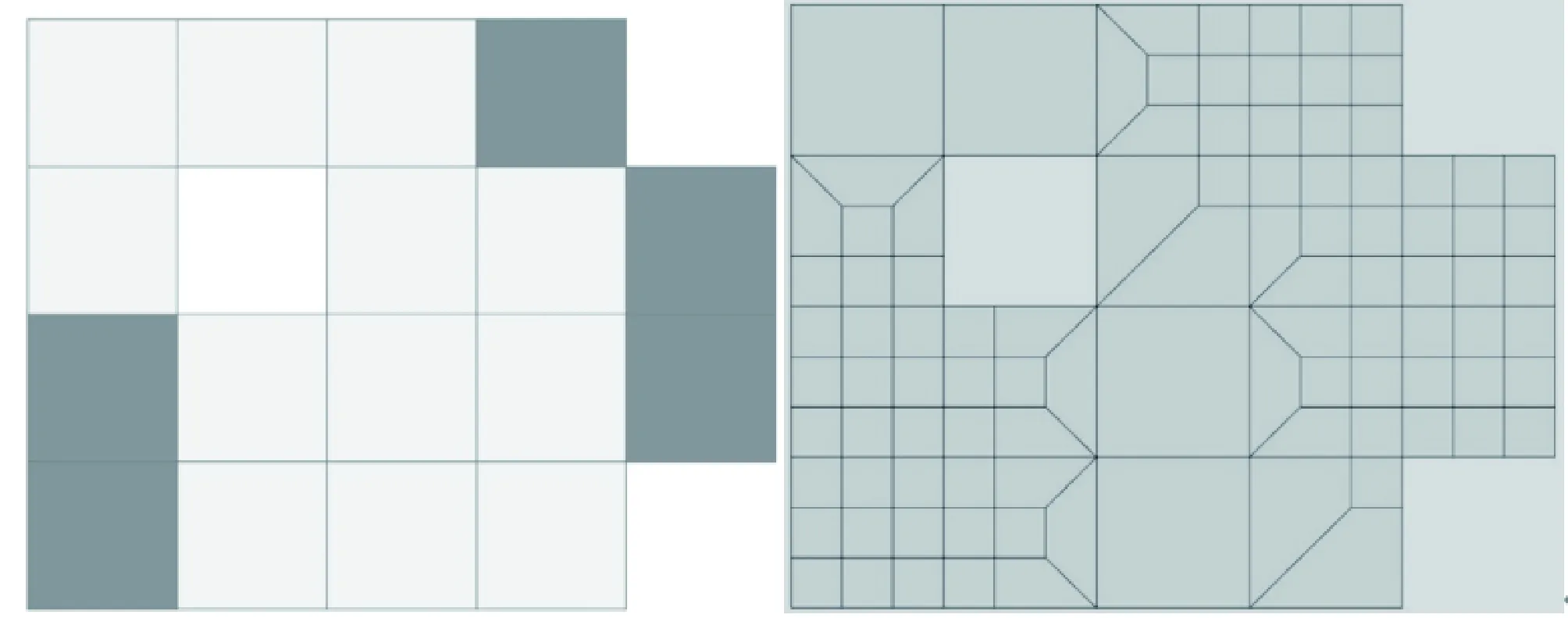
图5 原始网格(左)和根据模板加密一次以后的网格注:其中灰色标记单元做了完全加密。

本研究中的加密策略具体将基于单元顶点的标记数目进行选择不同的加密模板,如图6所示。在加密过程中,所有标记单元的顶点被标记为实心标记点,具有标记顶点的关联单元将逐个独立地加密,而不依赖于邻居单元的加密方式。值得一提的是,每个单元的加密并不会影响邻居单元,从而可以自动达成局部加密后的全局协调,实现正规网格。这种局部操作有利于程序实现,还可以进行并行网格调整。

图6 单元的6种加密模板注:根据单元顶点的标注方式,实心标注的顶点在某标记单元上。

根据图6中的加密模板,已经能够根据标记点对网格单元进行一次加密。为了处理单元需要多次加密的情形,还要给加密单元的顶点设置加密次数S(v), 初始S(v)=隶属单元的最大加密次数。加密后网格中顶点加密次数S(v)这样变化:对于加密前已经存在的顶点v,只需要将他们的加密次数减1即可;对于加密过程中产生的新节点,若新点在原网格单元的边上,则该顶点的加密次数设置为原单元边的两顶点的新加密次数的最小值;若新点在原网格单元的内部,则该顶点的加密次数为单元原4个顶点的新加密次数的最小值。只要重复执行以上加密过程并调整加密次数的值直至网格中不存在标记点,网格加密便完成了,详情见图4。

2.4 加密算法

经过上述的设计,加密策略可以产生正规且稳定的加密网格,其单元角度不会随着加密过程变得越来越小,这一点可以很容易地证明。这是因为图6中的所有模板都会在标记点周围生成一个与原单元相似的新单元,这可以控制加密过程中网格单元角度的变化,从而保证网格的稳定性。关于网格的正规性,首先指出:任意两个标记点之间的边均被三等分;任意一个标记点到网格边的中点的边均被二分;任意不包含标记点的网格边保持不变。因此,根据此规律以及标记点加密次数S(v)的计算方法,初始网格中边的划分方式是唯一确定的,即插入的点的数目以及位置是唯一确定的。据此可以证明,加密后网格的正规性,经过上述分析,总结基于加密模板以及加密次数设计的四边形网格加密算法如下。

步骤1:给每个点确定加密次数S(v)(确定标记点)。

步骤2:依据标记点组合情况从图7中挑选合适的加密模板并加密单元。

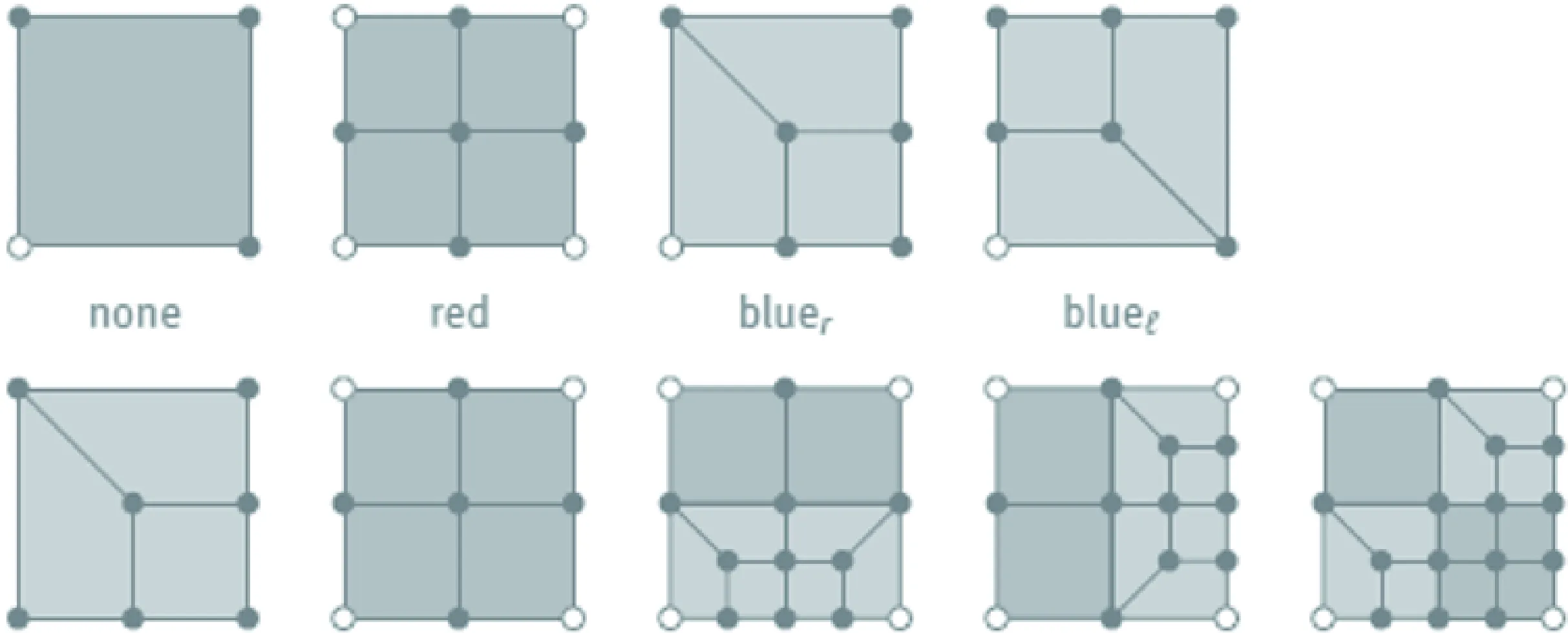
图7 单元加密模板

步骤3:更新加密后网格点的加密次数S(v)。

步骤4:重复步骤1—3,至所有点加密次数为0。

3 加密策略的程序实现和验证

3.1 二分策略

由于需要控制网格尺寸,在程序中采用了二分策略,即将单元边二等分,以便更好地加密。具体而言,如果单元被完全加密,将会产生4个单元。然而,在加密过程中需要考虑网格的整体协调性,因此需要在一些位置安置过渡单元。例如,如图8所示,左侧为原始网格,右侧为加密两次后的网格,其中标记单元被16等分,邻近单元也做了部分加密。

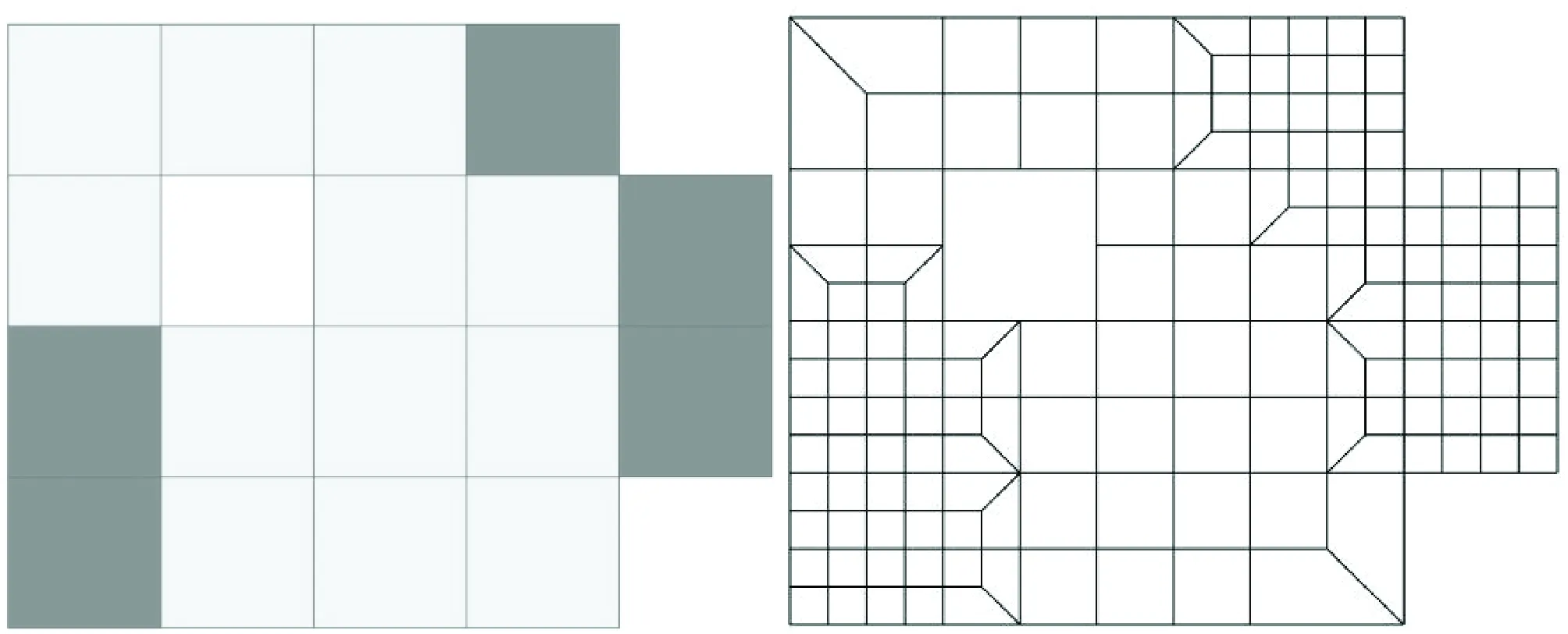
图8 原始网格(左)和根据模板加密二次以后的网格注:其中灰色标记单元做了两次完全加密。

3.2 两种基本单元类型

加密过程生成了两种基本单元类型,其中完全加密类型被定义为“田”字型,其对应原单元的所有边均已进行了加密。而过渡单元则被定义为“Y”字型,仅对两条边进行了加密。需要注意的是,当对一个“田”字型单元或一个“Y”字型单元进行加密时,加密方式并不是唯一的。为了确定加密方式,选择使用如图7所示的模板,并根据单元边的标记情况进行加密。如图9—10所示,在图中打叉的边表示标记加密的边,即使用图9来说明当“田”字型单元的边被标记时的加密方式,使用图10说明“Y”字型单元的加密方式。

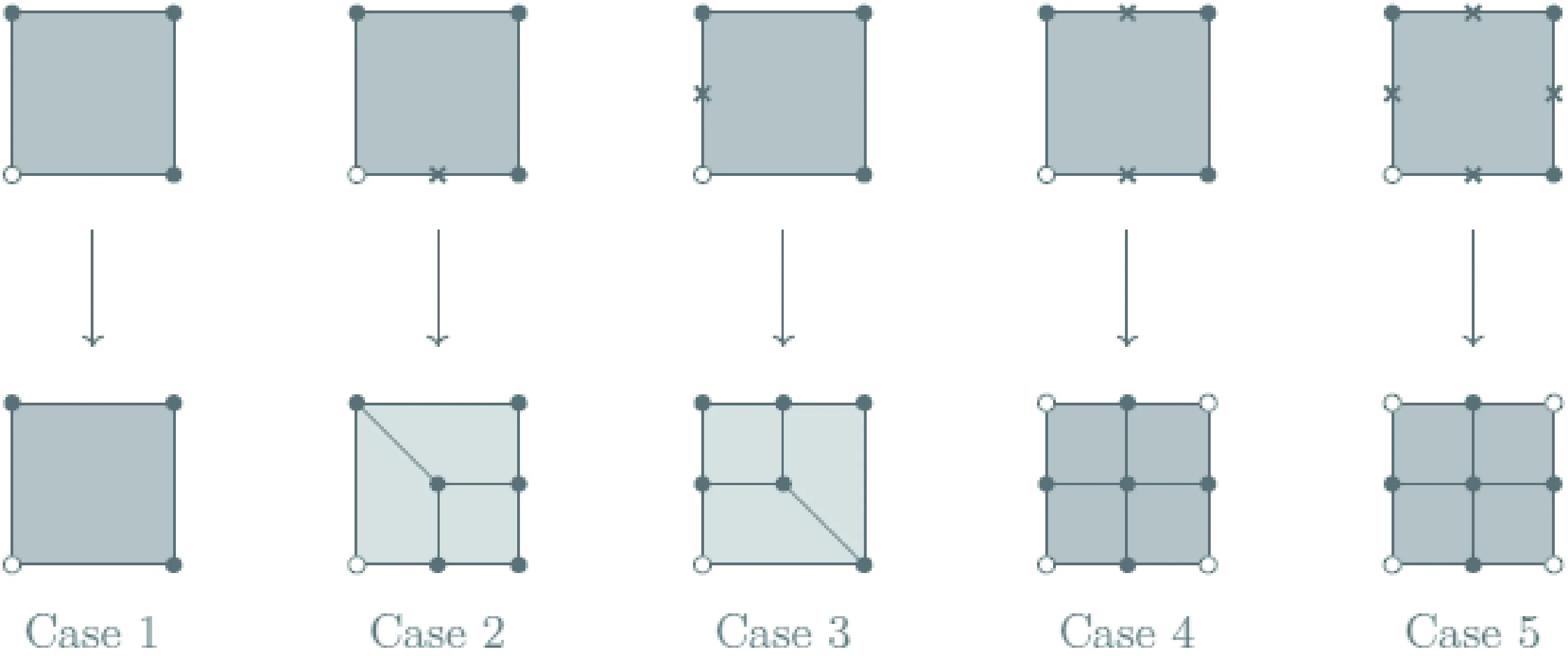
图9 “田”字型单元加密模板

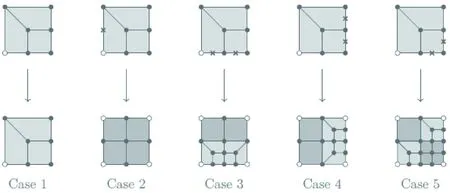
图10 “Y”字型单元加密模板

根据单元边的加密标记选择对应模板,逐个单元进行独立加密。该算法的实现并不依赖于邻居单元如何加密,因此能够保证加密后的全局协调。此外,所有的操作都是局部的,这有利于算法的并行实现。

3.3 验证算法

下面将通过一个算例来验证网格加密程序的基本功能。初始网格如图11所示,并选定其中部分单元(标记为深色)进行连续加密。在加密过程中,结果显示成功地应用了图7中的所有模板。运算表明,该加密方法可以成功地解决问题。

图11 初始网格

4 结语

结合程序实现和算例结果可知,所设计的四边形自适应网格局部加密算法可以根据单元边的加密标记而选择合适的模板,根据相应的模板,在加密单元的邻域中引入过渡单元,以消除悬点。并对具体网格的逐个单元进行独立加密,且不依赖于邻居单元,因此能够很好地保证加密后的整体单元协调性。此外,所进行的加密过程都是局部的,有利于算法的并行实现,并得到正确的计算结果。

[1]曲延鹏,张坤,陈颂英.MRT-LBM三重网格局部加密算法研究[J].北京理工大学学报,2018(5):441-448.

[2]刘维,刘宇迪,赵世梅.跨尺度预报模式的网格局部加密算法[J].解放军理工大学学报,2016(6):571-577.

[3]王川,赵成璧,唐友宏,等.NURBS曲面和隐式曲面求交的局部加密算法[J].科学技术与工程,2013(17):4826-4832.

[4]伍书重,莫思阳,张友良,等.数值流形法局部网格加密算法[J].科学技术与工程,2021(7):2850-2856.

[5]刘登学,张友良,丁秀丽,等.数值流形法中基于适合分析T样条的局部网格加密算法[J].岩土力学,2019(4):1584-1595.

[6]李红岩,王玉惠.基于超混沌系统的三维网格模型几何保留加密算法[J].现代电子技术,2018(7):90-964.

[7]蒲伟,王家序,周广武,等.卷吸速度方向与椭圆短轴成一夹角的弹流润滑渐近网格加密算法[J].西安交通大学学报,2014(9):95-1006.