若干倍图的2-距离和可区别全染色
王同昕,杨 超*,殷志祥,姚 兵
(1.上海工程技术大学 数理与统计学院/智能计算与应用统计研究中心,上海 201620;2.西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言

猜想1[5]对阶数至少为2的任意图G,有tndiΣ(G)≤Δ(G)+3.
猜想1对稀疏图[6]、无K4-子式图[7]、最大度至少为13的平面图[8]均成立.Cheng等[9]证明了最大度至少为14的平面图邻和可区别全色数不超过Δ(G)+2,进一步证实了猜想1;姚丽[10]将邻和可区别全染色进行推广,介绍了图的2-距离和可区别全染色,得到了路、圈、星、扇、轮、完全二部图的2-距离和可区别全色数.受上述研究启发,本文探讨几类倍图的2-距离和可区别全染色问题.
1 预备知识

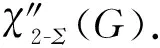

定义2[11]设G′是简单图G的一个拷贝,记G的顶点为ui,G′相对应的顶点为vi.若图G满足下述条件:
( i )V(D(G))=V(G)∪V(G′);
(ii)E(D(G))=E(G)∪E(G′)∪{uivj:ui∈V(G),vj∈V(G′),uivj∈E(G)},
则称D(G)为图G的倍图.
路P4的倍图D(P4)如图1所示.

图1 倍图D(P4)
2 主要工作
定理1设Pn表示阶为n(n≥4)的路,则

定义D(Pn)的一个6-全染色f如下:
由上述染色可得,S(u1)=6,S(v1)=12,这里S(u2),S(v2),…,S(un-1),S(vn-1)按照19,20,15,16,17,18循环,当n≡0(mod3)时S(un)=6,S(vn)=13;当n≡1(mod3)时S(vn)=7,S(un)=11;当n≡2(mod3)时S(un)=12,S(vn)=13.故D(Pn)中2-距离点的权重可区别.】
定理2设Cn表示阶为n(n≥3)的圈,则
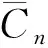
倍图D(C3)的一个 2-距离和可区别6-全染色如图2所示.
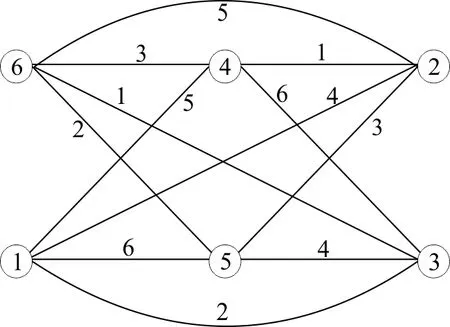
图2 倍图D(C3)的一个2-距离和可区别6-全染色
接下来讨论n≥4的情形.假设D(Cn)中存在一个6-全染色,则一共有6种全染色方案,而D(Cn)中与点u1距离小于等于2的点至少有7个,矛盾.故D(Cn)的一个正常全染色至少需要7种颜色.定义D(Cn)的一个7-全染色f如下:
情形1n=0(mod3).
由上述染色可得,S(u1)=21,S(V1)=18,这里S(u2),S(v2),S(u3),S(v3),…,S(un-1),S(vn-1)以19,20,15,16,17,18循环,S(un)=16,S(vn)=22.
情形2n=1(mod3).
由上述染色得,S(u1)=17,S(v1)=23,这里S(u2),S(v2),S(u3),S(v3),…,S(un-1),S(vn-1)以19,20,15,16,17,18循环,S(un)=18,S(vn)=22.
情形3n=2(mod3).
由上述染色可得,S(u1)=21,S(v1)=23,这里S(u2),S(v2),S(u3),S(v3),…,S(un-1),S(vn-1)以19,20,15,16,17,18循环,S(un)=27,S(vn)=22.
综上所述,f为D(Cn)的一个2-距离和可区别7-全染色.】
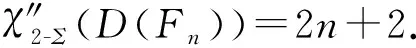

根据上述染色可得D(Fn)各点权重如下:

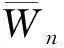
由上述染色可得D(Wn)(n≠8)中各点权重为:
即f为D(Wn)(n≠8)的一个2-距离和可区别(2n+2)-全染色.
当n=8时,上述染色方案中出现S(u1)=S(u2)=43的情况,此时用5重染点u1,得S(u1)=44≠S(u2)=43,由于其它点和边的染色未改变,故可得W8的一个2-距离和可区别18-全染色.
综上所述,定理得证.】

证明设

由上述染色可得,
即f为D(S2n)的一个2-距离和可区别(2n+4)-全染色.】
定理6设Km,n(3≤m≤n)为完全二部图,则
证明 情形1m=n.
设V(Kn,n)={ui,vi:i=1,2,…,n},E(Kn,n)={uivj:i,j=1,2,…,n}.由引理1可得,
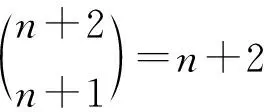
所以Kn,n的一个正常全染色至少需要n+3种颜色.下面构造Kn,n的一个正常(n+3)-全染色f:
由上述染色,容易验证:
故f为Kn,n的一个2-距离和可区别(n+3)-全染色.
情形2m 由上述染色可得: 故f为Km,n的一个2-距离和可区别(n+2)-全染色.】 由倍图的定义可知,D(Km,n)=K2m,2n,星Sn的倍图为完全二部图K2,2n,故由定理6直接可得下述结论: 推论1设Km,n为完全二部图,则


