Gorenstein 正则环上 Gorenstein 投射覆盖的存在性
张豫冈,曹天涯
(1.兰州工业学院 基础学科部,甘肃 兰州 730050;2.西北师范大学 计算机科学与工程学院,甘肃 兰州 730070)
0 引言
本文环R均表示具有单位元的结合环,所有的模均是某个环R上的左R-(酉)模.
覆盖与包络(也称逼近)理论的研究源于模的内射包络及投射覆盖的概念,目前已成为(相对)同调代数领域的基本课题之一.众所周知,在经典的同调代数中,著名的“平坦覆盖猜想”成立,即任意环上所有模都具有平坦覆盖.同时,任意环上所有模都具有内射包络.由Wakamutsu引理可知,任意环上所有模具有特殊的平坦预覆盖和特殊的内射预包络.另一方面,所有模都具有特殊的投射预覆盖,所有模具有投射覆盖当且仅当基环R是左完全环.受Holm 研究思路的启发,国内外许多学者研究了Gorenstein投射(预)覆盖、Gorenstein内射(预)包络和Gorenstein平坦(预)覆盖的存在性[1-7].值得一提的是,aroch等[5]证明了任意环上所有模都具有Gorenstein内射包络,并且任意环是GF-闭的;因为任意环上所有模都具有Gorenstein平坦覆盖[2],进而由Wakamutsu引理可知,任意环上所有模具有特殊的Gorenstein内射预包络和特殊的Gorenstein 平坦预覆盖.但是,任意环上所有模是否具有特殊的 Gorenstein 投射预覆盖(进而怎样的环满足其上所有模具有 Gorenstein 投射覆盖)仍然未知.
2014年,Enochs 等[8]将Beligiannis[9]称为左 Gorenstein环的环重新命名为左Gorenstein正则环.由文献[10]定理4.1可知,左Gorenstein正则环即具有有限左Gorenstein整体维数的环.作为具有有限左整体维数的环和Iwanaga-Gorenstein环的共同推广,左Gorenstein正则环上Gorenstein模类具有良好性质.由文献[11]引理5.1(1)可知,左Gorenstein正则环上所有模具有特殊的Gorenstein投射预覆盖.因此,自然地可以考虑如下问题:
问题A怎样的左Gorenstein正则环满足所有模具有Gorenstein投射覆盖?
本文定理1给出了上述问题的彻底回答.
定理1设R是左Gorenstein正则环,则如下结论等价:
(1)所有左R-模具有Gorenstein投射覆盖.
(2)R是左完全环.
Auslander最后定理说明,在任意 Iwanaga-Gorenstein环上每个有限生成模具有 Gorenstein投射覆盖.但是,由定理1可知,非完全的Iwanaga- Gorenstein环不能保证所有模具有Gorenstein投射覆盖.作为定理1的另一应用,我们给出交换Gorenstein遗传环是Gorenstein Artin代数的 Gorenstein同调刻画.
1 预备知识
用R-Mod 表示所有R-模的类,其中由所有投射、内射、平坦及FP-内射R-模构成的(子)类分别用P,I,F及FI表示,pdR(M),idR(M),fdR(M)和FP-idR(M)分别表示R-模M的投射、内射、平坦和FP-内射维数.
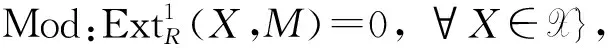
其中X,X′∈X且Y,Y′∈Y.
R-模M的X-预覆盖是指一个同态α:X→M,使得X∈X并且对任意的X′∈X,序列HomR(X′,X)→HomR(X′,M)→0是正合的.称R-模M的X-预覆盖α:X→A是X-覆盖,如果满足αf=α的自同态f:X→X都是同构.称A的X-(预)覆盖α:X→A是特殊的,如果α是满同态,并且Kerα∈X⊥.称模类X是(预)覆盖类(或特殊的预覆盖类),如果A中的每个对象都具有X-(预)覆盖(或特殊的X-预覆盖).称余挠对(X,Y)是完全的,如果X是覆盖类且Y是包络类,这里包络类是覆盖类的对偶.
称R-模M是Gorenstein投射的,如果存在一个由投射R-模构成的Hom(-,P)-正合的正合序列
…→P1→P0→P0→P1→…,
使得M≅Im(P0→P0).对偶可定义Gorenstein内射模.
用GP表示由所有Gorenstein投射R-模构成的类.分别称GP-(预)覆盖及特殊的GP-预覆盖为Gorenstein投射(预)覆盖及特殊的Gorenstein投射预覆盖.
近来,汪军鹏[12,13]研究了奇点范畴和相对于Ding模的稳定范畴之间的关系,并刻画了Gorenstein正则环.用1.G-gl.dim(R)表示环R的左Gorenstein整体维数,即所有R-模的Gorenstein投射维数的上确界和所有R-模的Gorenstein内射射维数的上确界这两个相等的值;维数silp(R)和spli(R)定义如下:
spli(R)=sup{pdR(M):M是内射R-模},
silp(R)=sup{idR(M):M是投射R-模}.
定义1[12]称环R是左Gorenstein正则的,如果R满足如下等价条件之一:
(1)silp(R)<∞且spli(R)<∞;
(2)1.G-gl.dim(R)<∞;
(3)存在一个非负整数n使得1.G-gl.dim(R)≤n.
定义2称环R是右Gorenstein正则环,如果R的反环Rop是左Gorenstein正则的.
易知环R是右Gorenstein正则环当且仅当R的右Gorenstein整体维数有限,这里R的右Gorenstein整体维数是指其反环Rop的左Gorenstein整体维数.
2 主要结论及证明
下述引理1给出了左Gorenstein正则环的性质,其意义平行于Gorenstein环的相应性质[1].
引理1([13,引理 3.9]) 设R是满足1.G-gl.dim(R)≤n的左Gorenstein正则环,则对任意的R模M,以下条件等价:
(1)fdR(M)<∞;
(2)pdR(M)<∞;
(3)idR(M)<∞;
(4)FP-idR(M)<∞.
而且,以上所有维数均不超过n.
引理1表明,在左Gorenstein正则环上每个投射模具有有限的内射维数,因而由文献[8]引理2.4可得如下Gorenstein投射模的刻画.
引理2设R是左Gorenstein正则环,M是R-模,则以下条件等价:
(1)M是Gorenstein投射模;
(2)存在正合序列0→M→P0→P1→…,其中每个Pi是投射模.
引理3设R是环,R-模的类X对直和因子封闭且P⊆X,则以下条件等价:
(3)X是特殊预覆盖类;
(4)存在完备的余挠对(X,X⊥).


下证余挠对(X,X⊥)的完备性.对于任意的R-模N,由前述证明可知,存在R-模的短正合序列
0→KN→XN→N→0,
其中KN∈X⊥且XN∈X.换句话说,余挠对(X,X⊥)具有足够的投射对象.因而由文献[8]命题7.1.7可知,余挠对(X,X⊥)亦具有足够的内射对象.所以,余挠对(X,X⊥)是完备的.

其中K∈X⊥且X∈X.通常的同调代数方法可以验证f:X→N是N的特殊的X-预覆盖.】
结合引理3和文献[11]引理 5.1(1)可得如下结论.
引理4设R是左Gorenstein正则环,则存在完备遗传的余挠对(GP,W),其中W表示所有具有有限投射维数的R-模构成的类.因而GP是特殊的预覆盖类.
引理4表明,在左Gorenstein正则环上每个模具有特殊的Gorenstein投射预覆盖类.
称一个环R是左(右)完全环,如果每个左(右)R-模具有投射覆盖;特别地,称环R是完全环,如果R是左、右完全环.
下面定理2包含了引言中的定理1,给出了问题A的彻底回答.
定理2设R是左Gorenstein正则环,W表示所有具有有限投射维数的R-模构成的类,则以下条件等价:
(1)模类GP是覆盖类;
(2)模类GP对正向极限封闭;
(3)(GP,W)构成完全的余挠对;
(4)每个投射维数有限的R-模M具有Gorenstein投射覆盖;
(5)每个内射维数有限的R-模M具有Gorenstein投射覆盖;
(6)每个FP-内射维数有限的R-模M具有Gorenstein投射覆盖;
(7)每个平坦维数有限的R-模M具有Gorenstein投射覆盖;
(8)每个平坦R-模M具有Gorenstein投射覆盖;
(9)R是左完全环.







显然,每个左(右)整体维数有限的环是左(右)Gorenstein正则环.由文献[1]定理9.1.11可知,每个(Iwanaga-)Gorenstein环(因而每个Gorenstein Artin代数)是左、右Gorenstein正则环.这里称环R是(Iwanaga-)Gorenstein环,如果存在非负整数n,使得R是n-Gorenstein环,即R是双边诺特环,并且R的双边自内射维数均不超过n.特别地,称Artin代数R是Gorenstein Artin代数,如果R作为环是Gorenstein环,等价地,如果R的双边自内射维数不超过n.
注记1( i )作为定理2的推论,我们有:一个左(右)整体维数有限的环是左(右)完全环当且仅当每个左(右)R-模具有Gorenstein投射覆盖.注意到存在非完全的整体维数有限的交换环(例如通常的整数环Z),因而在这样的环上的模类GP不是覆盖类.
(ii)由于Gorenstein Artin代数是Gorenstein正则环,并且是双边Artin环(因而是双边完全环),从而由定理2可知,在Gorenstein Artin代数R上所有左、右R-模均具有Gorenstein投射覆盖.
(iii)设R是Gorenstein环.由著名的“Auslander 最后定理”(文献[1]定理11.6.9)可知,每个有限生成R-模具有Gorenstein投射覆盖.另一方面,Gorenstein环是左Gorenstein正则环,因而由定理2可知,所有R-模具有Gorenstein投射覆盖当且仅当R是左完全环.因此,在非左完全的Gorenstein环上模类GP不是覆盖类.例如,通常的整数环Z是非完全的交换1-Gorenstein环,因而在环Z上模类GP不是覆盖类.
称一个环R是(Gorenstein)遗传环,如果R的任意左、右理想均是(Gorenstein)投射的,等价地,如果R的左、右(Gorenstein)整体维数不超过1.显然,每个遗传环是Gorenstein遗传环,并且每个Gorenstein遗传环是左、右Gorenstein正则环.另一方面,易知每个1-Gorenstein Artin代数是Gorenstein遗传环.
推论1设R是交换Gorenstein遗传环,则以下条件等价:
(1)R是1-Gorenstein Artin代数;
(2)模类GP是覆盖类.



