基于多尺度LBP 算子的大理石纹理分割算法

邹智伟， 张战成， 姚浩男， 徐少康

（苏州科技大学电子与信息工程学院，江苏 苏州 215009）

“源于自然，超越自然”是建筑类人造石材装饰的价值追求。 人造大理石的图案通常采集于天然石材，先经设计师修饰出图，然后经布料系统处理，分成多个颜色通道在模具中喷料制造。 传统布料系统依赖人工对大理石图片进行纹理分割，成本高昂，同时分割结果也受个人主观因素影响，造成了新花色设计周期长、生产效果和原始设计效果偏差大等问题。 利用图像处理技术对图片进行智能分割，代替传统的人工抠图，实现大理石的智能布料，是智能制造的发展方向。 传统的图像分割算法只考虑了像素值信息而忽视图像中形状信息和纹理信息[1]，不符合纹理分割的要求。 由于天然大理石纹理具有随机和不规则的特点，并且大理石纹理很难用高层语义特征描述，基于深度学习的FCN（Fully Convolutional Networks）、APC-Net（Adaptive Pyramid Context Network）等场景分割算法很难直接用于大理石的纹理分割。 目前纹理分割方法主要分为以下几类：基于灰度共生矩阵（Grey-Level Co-occurrence Matrix，GLCM）的纹理分割算法[2]、基于Gabor 滤波器的纹理分割算法[3]和基于局部二值模式（Local Binary Pattern，LBP）的纹理分割算法[4]等。

大理石图像纹理的底层视觉特征表示[5]和聚类分割是实现分离的关键步骤。 常用的特征描述算子有灰度共生矩阵、Gabor 滤波器、LBP 算子等。 灰度共生矩阵是像素距离和角度的矩阵函数，它通过计算图像中一定距离和一定方向的两点灰度之间的相关性，来反映图像在方向、距离、变化幅度及快慢上的综合信息，由此代表纹理信息。 Haralick 等人[6]提出了用灰度共生矩阵来描述纹理特征，用灰度和梯度的综合信息提取纹理特征，将图像的梯度信息加入到灰度共生矩阵中，使共生矩阵包含图像的纹理信息及排列信息，但计算过程太过冗余，计算效率低下。 Pratap T 等人[7]使用不同方向的Gabor 滤波器提取纹理特征，图像通过Gabor 滤波器处理之后，在图像空间域上，将高斯核函数和正弦平面波相乘得到纹理特征信息。 在频域上，纹理特征信息反映在不同方向和不同尺度上的多向性特征。 Gabor 能够提供良好的方向选择和尺度选择特性，而且对于光照变化不敏感，对光照变化有良好的适应性。 如上所述，需要构造多尺度、多方向的Gabor 滤波器，这会使图像尺寸、特征维度成倍增加，产生冗余数据，使特征匹配更加困难。Ojala T 等人[8]则使用LBP 算子提取纹理特征，该算子具有光照不敏感性、灰度不变性和旋转不变性，且鲁棒性强。不同于GLCM 和Gabor 滤波器计算冗余、特征维数高，LBP 算子计算时间快、消耗内存小，LBP 算子的缺点是易受到噪声影响，为了克服该缺点出现多种LBP 变体，如局部三值模式（Local Ternary Pattern，LTP）[9]、ELBP[10]和CLBP[11]。 但LBP 算子还是受算子尺度的影响，难以捕捉宏观纹理信息和纹理变化。

常用的聚类算法主要有K 均值聚类（K-means）[12]、模糊C 均值（Fuzzy C-means，FCM）[13]和高斯混合模型（Gaussian Mixture Model，GMM）[14]等。 K-means 算法的优势在于它的速度非常快，因为只需要计算点和簇中心之间的距离，它的缺点是必须人工选择聚类数量且聚类效果很大程度取决于聚类中心的初始位置；对于满足正态分布的数据，FCM 算法的聚类效果更好， 但对孤立点十分敏感且算法性能同样依赖初始点；GMM 算法与常见的K-means 聚类方法类似，但K-means 属于硬聚类，结果中只包含每个像素点属于某个类的硬划分。 在此基础上高斯混合模型则可以给出每个像素点属于多个类的概率， 其包含的信息量远高于K-means和FCM 算法，属于软聚类。 该模型优点在于，当某元素分配给两个簇的概率相同或非常接近时，可以通过主观选择或者设置可变阈值来获得更准确的结果。

原始LBP 算子在固定尺度上提取局部信息，存在两个问题：第一个问题是单一尺度不能有效的获取大尺寸且连续的纹理，解决该问题的一种方式是增大算子尺度[15]；第二个问题是在构造灰度特征向量时，仅将边缘像素和中心像素进行比较，而忽视边缘和中心之间的内部像素，丢失大量信息。 受到深度学习中空洞卷积[16]和特征金字塔[17]的启发，将多分辨率特征联结，增大感受野从而捕获大尺度纹理特征。 笔者提出MLBP（Multiscale Local Binary Pattern）算子解决这两个问题。 MLBP 是多个子尺度LBP 算子的叠加，不同于传统方法使用边缘的连续像素作为采样点，而使用子尺度采样点的组合，且选择大尺度算子的同时保留内部子尺度算子，减少特征丢失。在MLBP 中，不同尺度的纹理特征会被不同的子尺度算子捕捉，不同子尺度算子能提取纹理的不同变化。

1 算法模型

将MLBP 算子提取的大理石图像纹理信息作为特征向量，通过高斯混合模型对特征向量分布进行分析，使用EM 算法计算GMM 参数， 通过参数计算某个样本属于某个聚类的概率， 挑选最大概率作为该样本的Label，则获得分割结果。 算法整体流程如图1 所示。

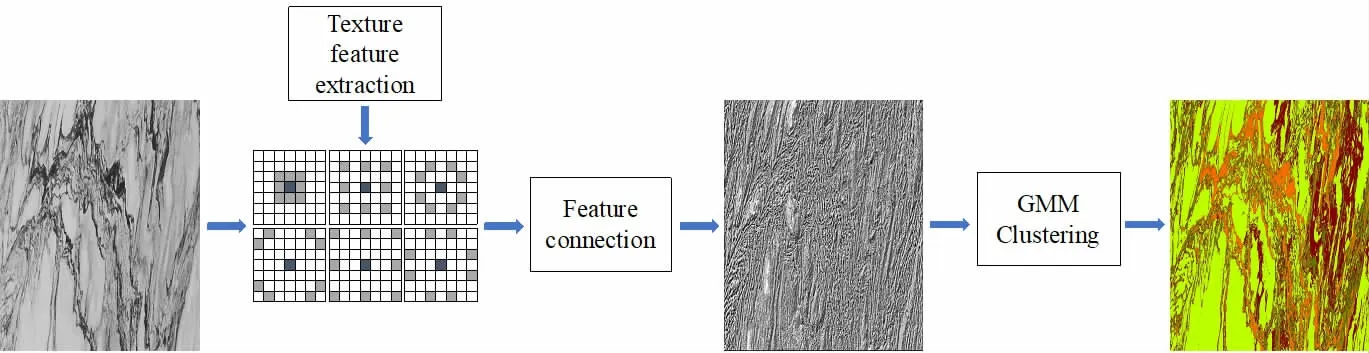
图1 算法流程图

MLBP 算子基于LBP 算子，如图2 所示，5×5 MLBP 算子由3 个子尺度算子组成，分为外部子尺度算子和内部子尺度算子，不同于LBP 算子使用16 个连续邻域像素作为采样点，而是将24 个边缘采样点分解成3个邻域像素的组合，每个组合由8 个采样点组成，对应3 个子尺度算子。 计算过程如下：

图2 MLBP 5×5 算子

首先，将图像转为灰度矩阵，每个像素点是值为[0，255]的一维向量，子尺度算子在灰度矩阵上对每个像素点进行计算，移动步长为1。 计算公式为

其中k代表像素点，总像素点个数为K，I（*）是指该点的灰度值，p代表的是采样点（不同子尺度算子的采样点不同），gt（*）代表门函数。 将中心点和邻域采样点进行比较，大于中心点的为1，小于中心点的为0，类似门控逻辑。 将8 位二进制数组合并转换为10 进制数，即该像素点的新灰度值，计算过程类似卷积操作，最后将多个子尺度算子提取的纹理向量级联得到最终纹理向量。

5×5 MLBP 是3 个子尺寸算子的组合，7×7 尺度下是6 个（如图3 所示），这不仅考虑边界像素，还考虑内部块的像素来构造特征向量，采用8 个采样点的组合保证灰度值区间为[0，255]，通过不同大小的子尺度算子能增加感受野，使获取的特征更加完整连续，即单个子尺度算子提取不到的特征其他子尺度算子能够提取，领域像素的不同组合可以有效捕捉纹理特征的变化，脱离了原始LBP 算子的局部性。

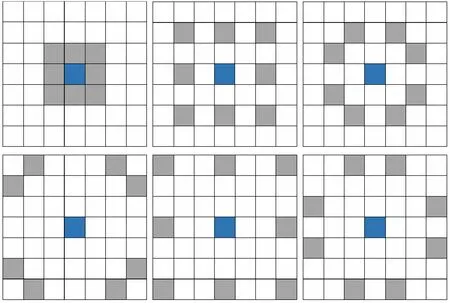
图3 MLBP 7×7 算子

2 实验结果及分析

文中实验选取厂家提供的彩色大理石样板图作为数据集，将原图RGB 颜色空间转为YUV 颜色空间，选取Y 通道进行纹理分割，包含两种像素尺寸规格：3 545×17 618 和1 601×2 015，含有鱼肚白和北冰洋等不同风格的大理石图像。 为了体现文中算法在纹理分割上的优越性，将该算法分割结果与基于LBP 算子的图像分割算法FCM-LBP、K-means-LBP 和主流语义分割算法FCN 对比，再详细对比不同纹理描述算子的灰度图结果来展现MLBP 算子相比普通LBP 算子的优势。

2.1 实验结果

如图4 与图5 所示，大理石图像相比普通图像具有丰富的纹理语义信息和复杂的位置信息。 如图4（c）和图5（c），FCN 语义分割算法很难将纹理特征从背景中分离，纹理特征发生错位，图像整体信息比较混乱，该语义分割算法不适合大理石纹理分割。LBP 算子受限于固定尺寸，在捕获小纹理特征的同时会损失大纹理特征，导致提取的纹理特征不完整，如图4（d）-图4（h）中FCM+LBP、K-means+LBP 和GMM+LBP 分割算法结果中线条出现断续，纹理边缘特征也有一定的损失；当分割目标差异较小时难以区分噪声和斑点类型纹理的区别，损失了大量的纹理信息；分割复杂纹理的边界时，在纹理和背景的界限上存在一定的过分割区域，分割时难以区分不同尺寸特征，噪声点和异常点偏多，鲁棒性较差。图4（f）-图4（g）受到聚类算法的影响，在数据较大时容易造成局部最优解，对孤立点非常敏感，分割结果存在许多噪声点，且分割效果非常依赖于聚类中心的初始化。 文中基于MLBP 提取纹理特征并利用GMM 进行聚类，与FCM 和K-means 不同，GMM 受噪声影响小，抭干扰能力强，如图4（h）-图4（i）。而MLBP 加入了子尺度算子，能够提取不同尺度的纹理特征且捕获到纹理的变化，从而获得更加准确的纹理特征，如图5（i），清楚地将纹理线条和背景区分，纹理线条完整且连续，噪点少，近似标签图。

图4 不同分割算法的分割结果

图5 不同分割算法的细节对比

如图6 所示，对比不同子尺度算子提取的纹理特征，可以看出每个子尺度算子捕获了不同尺度的纹理，大尺度算子获得较大的纹理信息，小尺度则捕捉小纹理信息。 图6（a）中，LBP 算子提取的特征局限于固定尺度，捕获的纹理特征并不完整，且纹理变化单一，而MLBP 中多个子尺度算子的结合完全提取图像的重要特征。 在同一时刻，某一个子尺度捕获不到的纹理信息另一个子尺度可以捕获到，这是多分辨率提取特征的一个重要特性。观察图6（b）中各个结果，可以看出背景和前景纹理的变化，不同子尺度算子捕捉到纹理不同方向的变化，而LBP 算子无法捕获纹理的变化。

图6 LBP、MLBP 7×7 算子纹理灰度图对比

2.2 实验分析

为了更好地定量评价每个方法的分割效果，文中使用像素精度（Pixel Accuracy，PA）、均像素精度（Mean Pixel Accuracy，MPA）、平均交并比（Mean Intersection over Union，MIoU）作为分割结果的评估标准。 PA 是计算标记正确的像素占总像素的比例；MPA 是一种逐像素标记的精度标准， 它是PA 像素精度的简单提升，计算每个类中被正确分类像素数的比例，之后求所有类的平均；MIoU 指在每个类别上计算IoU 值（真实值与预测值的交集/真实值与预测值的并集），最后进行平均操作。

从表1 中可以看出，在大理石样板数据集的实验中，FCN 语义分割算法精度较低，且空间位置上特征错位严重，不适合大理石纹理分割；将LBP 算子和FCM、K-means、GMM 结合的算法优于FCN 算法，但在细小纹理上分割上不够精确，难以将复杂的纹理从背景中分离出，导致纹理分割结果出现杂乱、断续等问题；文中提出的MLBP 算子将多尺度纹理特征融合起来，能清晰、完整地将连续纹理特征提取，在不同纹理风格的大理石数据集中平均分割精度均是最优， 基于MLBP 的算法相比FCN 分割算法均像素精度 （MPA） 提高了7.6%、8.1%、14%，对比基于LBP 的算法提高了6.6%、6.4%、3.1%。 最终文中算法比FCM-MLBP 提高6.4%，比K-means-MLBP 提高5.9%，均值正交比（MIoU）提高了8.6%、8%。

3 结语

面向大理石图像的纹理特征提取，设计了改进的LBP 算子MLBP，该算子通过融合多个子尺度算子提取的纹理信息，提高了LBP 算子对纹理的描述性，同时保留LBP 算子不受图片的光照、角度等因素影响的优点。 基于GMM 对纹理图片的MLBP 特征进行无监督聚类，实现了大理石纹理的自动分割。 在真实的大理石图片上进行纹理分割实验，实验结果表明，基于MLBP 方法结合GMM 相比FCN、FCM 和K-means 分割算法更加接近于标签分割结果，满足了工业生产的需求。 文中算法仅在鱼肚花纹和麻石花纹上进行了实验，更多风格的纹理图像分割的效果有待进一步验证。