分数阶PID控制在电动变载荷加载系统中的应用

刘福才, 王海澎

(燕山大学 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)

0 引 言

摩擦与磨损是生活中普遍存在的问题,在机器或是装备的运行中,相互接触的零部件之间的摩擦磨损现象是不可避免的。它会造成机械能损耗、产生噪音,对零部件造成变形、摩擦,影响其寿命[1]。摩擦磨损试验机是实现对一种特性材料在给定的条件下对摩擦磨损性能的探究,并能求得摩擦力与摩擦系数的模拟试验机。摩擦磨损试验机的出现对生产中减少能源损耗、提高生产效率等方面起着重大作用。然而研究摩擦磨损试验机的关键是对加载压力的控制,目前试验机主要存在机械、气动和电动3种加载形式[2]。随着电机制造水平和控制技术的不断提高,以电机作为驱动力的电动加载技术逐渐成为时代潮流。相比于机械式加载控制精确度低、无法实现变载荷加载和气动式存在空气可压缩性、气体流动的复杂性等问题,电动加载技术具有加载精确度高、跟踪速度快、结构简单、成本较低等优点。但电动加载系统存在强耦合、电机内部的高度非线性化以及加载过程中的多余力干扰等问题。为解决以上问题,更好地实现电动加载系统的控制性能,诸多学者对其进行了研究。文献[3]提出基于结构不变性原理,实验结果表明引入舵机的轴角速度作为前馈补偿后,能够有效地减小电机多余力矩的干扰。文献[4]构造了小脑模型神经网络(cerebellar model articulation controller,CMAC)与模糊控制相结合的复合控制方法,提高了系统的稳定性和鲁棒性。文献[5]提出了一种以速度闭环、转矩闭环以及位置闭环补偿的复合控制策略,其中转矩闭环采用模糊自适应PID控制算法。通过实验,复合控制方法在保证了加载精确度和动态性能的前提下,具有很强的鲁棒性和抗扰性。文献[6]采用自抗扰控制对四旋翼无人机在受到内部参数以及外部环境干扰的前提下进行测试,结果表明,所用的自抗扰控制算法有效地降低了外来干扰,提高了系统的准确性。上面涉及的几种控制算法虽然能有效地降低干扰性,起到不错的控制效果,但其存在控制器设计繁琐,推导计算量大等问题,因此本文采用分数阶PID控制(fractional order PID,FOPID),FOPID控制结构简单、易于理解、应用方便,较普通PID控制多了2个自由度[7-8],进一步扩大了参数整定范围,提升了控制能力和控制精确度,使其具有更好的动态性能和鲁棒性,提高了控制效果。

1 试验机加载系统模型分析

1.1 加载系统原理

试验机的加载系统主要由伺服电机及其驱动器、压力传感器、电动缸、摩擦压头和样品台组成。其中压力传感器内置于电动缸中,装置示意图如图1所示,工控机通过PCI-1710U板卡对压力传感器产生的压力信号进行采集,将采集到的压力信号利用所编写好的程序代码进行数据去值滤波处理并同给定的期望输入信号做差求得误差信号。然后将误差信号经过分数阶PID控制算法所产生的输出信号经过转换后通过PCI-1720U模拟量输出卡发送-10 V到+10 V的转矩指令作用于伺服电机驱动器,伺服电机驱动器接到转矩指令后驱动伺服电机进行旋转运动,伺服电机通过丝杠将其旋转运动转化为电动缸竖直方向的直线运行,从而实现摩擦压头对样品台的加载试验。

图1 电动加载系统实验装置示意图

1.2 加载系统数学模型

伺服电机的电压平衡方程为

(1)

电机电枢反电动势为

E=Keω。

(2)

电机的转矩平衡方程为

(3)

电磁转矩可表示为

Tm=KTi。

(4)

式中:U为电机电枢电压;i为电机电流;R为电枢纽回路总电阻;E为电枢反电动势;Ke为电机反电动势系数;ω为电机旋转角速度;Tm为电动机电磁转矩;J为转动惯量;B为电机阻尼系数;TL为电机轴输出转矩;KT为电动机转矩系数。

由式(1)～式(4)可知伺服电机模型传递函数为

(5)

由文献[9]电动缸输出轴直线位移为:

(6)

压力传感器模拟输出值为

F=Kfy。

(7)

式中:h为滚珠丝杠导程;Kf为压力增益。

由式(5)～式(7)得试验机加载系统开环传递函数为

(8)

1.3 加载过程中摩擦力与摩擦系数的获取

本试验机摩擦力的获取采用间接测量方法,首先将传动系统中的伺服电机以60 r/min的转速带动样品台空载运行,获得其电机空载转矩T0,然后加载系统进行加载试验,获得电机在力加载情况下的输出转矩T,并由游标卡尺测量加载压头距样品台旋转中心的距离R,则加载过程中的摩擦力f和摩擦系数μ可以表示为:

(9)

式中FN为加载压力。

2 分数阶PID控制器

2.1 控制器设计

FOPID是由Podlubny最早提出的[10],其在继承了传统PID控制的基础上新增了积分阶次和微分阶次两个可调参数,增加了控制器的调节范围,改善了控制器的性能。其结构框图如图2所示。

图2 FOPID控制器结构框图

FOPID微分方程表达式为

u(t)=Kpe(t)+KiD-λe(t)+KdDμe(t)。

(10)

式中:u(t)为控制器输出;e(t)为控制器输入;λ和μ为控制器的积分阶次和微分阶次;Kp、Ki、Kd为控制器增益参数。

控制器传递函数为

C(s)=Kp+Kis-λ+Kdsμ。

(11)

当λ和μ取不同值时,可以得到分数阶PID控制器的不同形式,如图3所示。由图可知,整数阶PID控制器只是分数阶PID控制器λ和μ取值为0或1的4个特殊点,因此分数阶PID参数整定范围更大,控制更加灵活,能更好地调节系统的动态性能,达到最佳的控制效果。

图3 λ、μ参数取值图

2.2 分数阶PID控制系统稳定性分析

一般来说,对于任何控制系统要稳定的充要条件是特征方程根位于S平面的左半面,但是分数阶系统的稳定性不同于整数阶,由Matignon的稳性定理可知,一个稳定的分数系统可能在S平面的右半部分有根。下面进行稳定性详细分析[11]：

一般分数阶系统特征方程为

(12)

(13)

由上式可知,通过代数转换将S平面的分数阶系统特征方程转化为σ平面的整数阶系统形式,从而能够间接使用劳斯判定准则判定系统稳定的充要条件为

(14)

将得到的分数阶系统稳定性区域和传统整数阶系统的稳定性区域做比较,如图4所示,可以看出,分数阶控制系统的稳定区域比整数阶控制系统的稳定区域范围要广,更加灵活可控。

图4 控制区域稳定示意图

2.3 实现方式

由于分数阶微积分算子是一个复变量s的无理化函数,其特征方程一般来说不是常规的多项式,在数值仿真与实际应用中不能够直接应用,因此用一个有限的微分方程来近似是分数阶微积分算子数字实现的关键[12]。本文采用Oustaloup近似化方法[13],假定选定拟合频率段为(ωb,ωh),其近似的有理传递函数模型为

(15)

其中:

(16)

式中:γ为分数阶阶次;2N+1为近似化次数。

2.4 控制器参数整定

由于分数阶PID控制器多了2个可调参数,使得控制器的控制更加灵活,但是也给分数阶PID控制器的参数整定造成了困难,只有合理地选择参数才能达到更理想的控制效果。本文将粒子群优化算法用于分数阶PID控制器中,以此对控制器参数进行优化整定。粒子群优化算法(particle swarm optimization,PSO)是1995年由Eberhart和Kenney通过模拟鸟类捕食行为而提出的一种群体智能优化算法[14]。在一个D维目标搜索空间中,有N个粒子组成一个粒子群体,第i个粒子的位置和速度为xi=(xi1,xi2,…,xiD)和vi=(vi1,vi2,…,viD),该粒子在整个搜索过程中所经历的最优位置称为个体极值pbest=(pi1,pi2,…,piD),粒子群体目前搜索的最优位置称为全局极值gbest=(pg1,pg2,…,pgD),在迭代过程中粒子通过自身的个体极值和群体的全局极值来更新自己的速度和位置,直到满足设定好的迭代终止条件,得出最优解并引用适应度函数作为评价因子,具体更新公式如下:

(17)

式中:i=1,2,…,N为粒子数;d=1,2,…,D为向量维数;k为当前迭代次数;c1,c2为非负的权重系数;r1,r2是分布于[0,1]区间的随机数;ω为惯性权重因子,用来调节算法的全局和局部搜寻能力。一个较大的惯性权值有利于全局搜索,而一个较小的惯性权值则更利于局部搜索。通常取权重系数ωmax=0.9,ωmin=0.4时算法性能最好,在合理的迭代次数里寻找全局最优值能力较好,所需迭代次数最少[15]。惯性权重由 0.9递减至 0.4,迭代初期保持了较强的全局搜索能力,而迭代后期有利于算法进行更精确的局部搜索。

目前常采用ω惯性权重公式为

(18)

式中:tmax为最大迭代次数;t为当前迭代次数。

虽然该方法让惯性权重不再是一个固定值,使得迭代过程中前期全局搜索能力增强,后期局部搜索能力增强,但惯性权重的变化率是固定值,可能会在较强的搜索条件下不能更好寻求最优值。本文在上式以及文献[16]的启发下,对惯性权值进行改进,令:

(19)

改进之后惯性权重变化率不再是固定的,引入rand函数体现了粒子群搜索过程的随机性。在粒子群的搜索初期,ω变化较慢,取值较大,加大了粒子的全局搜索能力;后期ω变化较快取值较小,提高了局部搜索能力,这样利于算法跳出局部最优而求得最优解,提高了算法的求解精确度。

适应度函数选用ITAE积分评价函数[17],即

(20)

式中e(t)为误差。

3 实验验证

为了更进一步地探究分数阶PID控制在实际系统中的控制效果,在电动变载荷摩擦磨损试验机平台上进行加载实验,分别采用恒值、三角波、方波、正弦波4种不同的典型信号作为加载系统载荷的期望跟踪曲线,实验平台如图5所示。分别在样品台静止和旋转时进行加载试验,样品台旋转相当于对加载系统在加载实验时引入了外部干扰。实验中设定传动系统中的伺服电机以60 r/min的转速带动样品台进行旋转实验,并通过工控机实时读取并储存加载实验数据,由旋转伺服电机转矩值及电动缸加载的压力值求得加载过程中的摩擦力和摩擦系数,并通过数据进行绘制相应曲线的加载载荷跟踪曲线、误差跟踪曲线和摩擦力与摩擦系数曲线。

图5 电动变载荷加载系统实验装置示意图

3.1 恒值加载

图6为在加载实验载荷F=100 N的恒值信号下样品台在静止时和旋转时加载压力的跟踪曲线及误差曲线图。

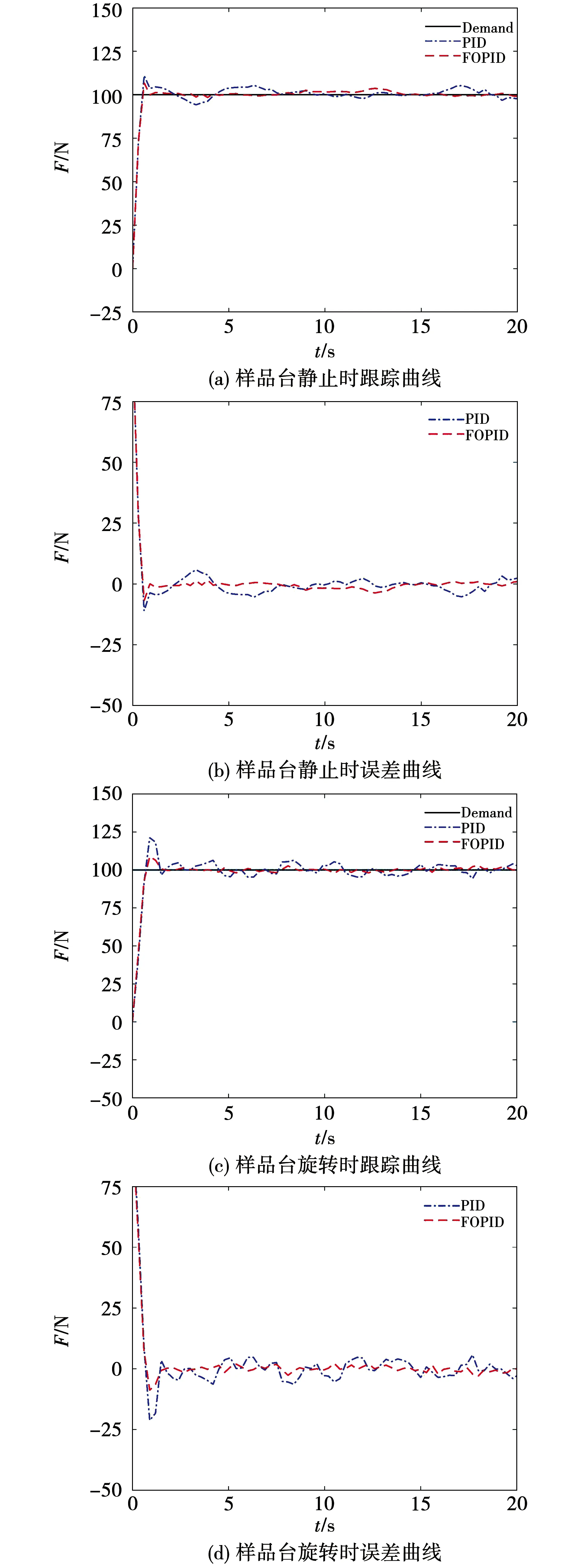
图6 恒值加载实验曲线图

由图6可知,分数阶PID控制较传统PID控制反应速度快、超调量小,在有外部干扰的情况下,FOPID能更好地减小系统的振荡,保证系统的稳定性。图7为在不同恒值力加载实验条件下摩擦力与摩擦系数曲线图。

图7 恒值下摩擦力与摩擦系数曲线图

可以看出,恒值力越大,加载过程中的摩擦力越大,摩擦系数越小,曲线走势和压力跟踪曲线类似。

3.2 三角波加载

图8为加载载荷信号幅值F=50 N,周期T=6 s的三角波信号下样品台在静止和旋转时的压力跟踪曲线及误差曲线。

图8 三角波加载实验曲线图

由图8可知,在三角波加载条件下,曲线振荡相对较大,FOPID控制在曲线的尖端突变处的误差相对较小,曲线跟踪效果优于PID控制。图9为三角波信号在不同幅值力加载过程中的摩擦力与摩擦系数曲线图。从图中可知,摩擦力曲线与加载力的跟踪曲线类似,加载力越大摩擦力就越大,摩擦系数的变化相对平稳,只在加载力曲线最底端发生突变。

图9 摩擦力与摩擦系数曲线图

3.3 方波加载

图10为输入加载载荷信号幅值F=100 N,周期T=6 s的方波信号下样品台在静止和旋转时的压力跟踪曲线及误差曲线图。

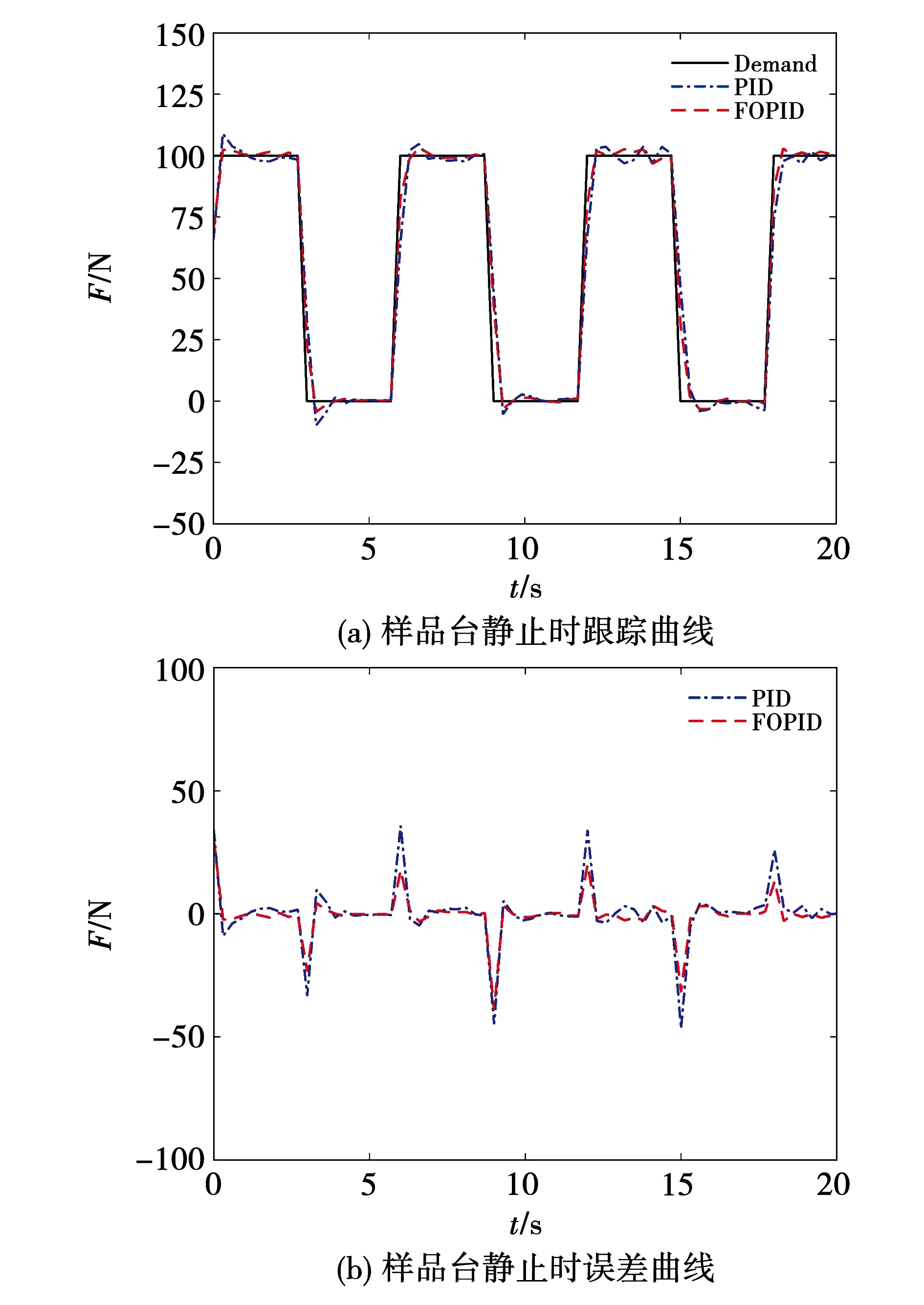
图10 方波加载实验曲线图

由图10可以看出,曲线在突变处具有一定的滞后性,FOPID控制的超调量比传统PID控制小,响应速度快,在引入外部干扰后,曲线的误差变大,但FOPID仍能展现良好的跟踪效果。

图11为方波信号在加载力幅值不同时加载过程中的摩擦力与摩擦系数曲线图。由图可知,摩擦力在波形突变处变化较大且摩擦系数在信号发生阶跃突变处变化较剧烈,从侧面反映出加载力跟踪在突变处较为振荡。

图11 摩擦力与摩擦系数曲线图

3.4 正弦波加载

图12为输入加载载荷信号幅值F=200 N,周期T=6 s的正弦信号下样品台在静止和旋转时的压力跟踪曲线及误差曲线。由图可知,在传统PID控制下曲线在峰值处出现了明显的滞后性;在引入外部干扰后,曲线误差虽然变大,但FOPID控制的曲线较为光滑平稳,误差相对较小,能够更好地对加载系统实时控制跟踪。图13为正弦信号在加载力不同时加载过程中的摩擦力与摩擦系数曲线图。

图12 正弦波加载实验曲线图

图13 摩擦力与摩擦系数曲线图

从图13可以看出,正弦波的摩擦力曲线和三角波形状类似,但摩擦系数在峰谷处变化较大,且加载力越小突变越剧烈,从侧面说明了加载力越大,曲线的误差越小,其跟踪效果越好。

4 结 论

针对电动加载系统中存在的强耦合、多余力干扰等问题,在传统PID控制的基础上提出了分数阶PID控制,对分数阶系统进行了稳定性分析和实现方案的设计,并利用改进惯性权重之后的粒子群优化算法对控制器的参数进行优化整定。对分数阶PID控制进行了模拟仿真,同时为了弥补现有文献只通过仿真验证分数阶PID的不足,将其应用于电动变载荷摩擦磨损试验机平台上,把仿真与实验结果和传统PID控制进行对比,可知分数阶PID控制响应更快,稳态精确度更高,更好地提高了电动变载荷系统的动态性能和鲁棒性。