车联网环境下匝道汇入区瓶颈换道优化

胡祥旺， 倪 颖， 孙 剑

（1. 苏州大学 轨道交通学院，江苏 苏州 215100；2. 同济大学 道路与交通工程教育部重点实验室，上海 201804）

高快速路汇入区（即合流区）是道路交通路网中的常见瓶颈之一，汇入瓶颈的失效会加剧高快速路拥堵程度、增加行程时间，同时失效导致的交通振荡向上游传播会增大速度差诱发新的事故，汇入区瓶颈交通流运行管控优化对于提升出行效率和安全均有重要意义。汇入瓶颈的失效表现为通行能力下降［1］或早发性失效现象［2］，大量实证研究表明触发瓶颈失效的原因为车辆的低速汇入行为、速度方差过大、加速车道末尾强迫换道且拥堵横向蔓延、驾驶行为的个体异质性和车道异质性等［2-4］。传统的匝道信号控制和主线可变限速关注交通流的流量、密度、速度，属于宏观的集计式控制，即所有车辆遵循同样的控制措施，无法全面且实时地感知微观交通状态变化因而改善效果有限。新兴的智能网联汽车技术（connected and autonomous vehicles， CAV）赋予了车车通信和车辆精确控制的能力，为汇入区瓶颈基于个体的精细化控制提供了可能性。目前CAV 环境下汇入区瓶颈交通流改善研究是热点问题，其特征可总结如下：

（1） 大部分研究关注匝道车辆与主线外侧车辆的协同汇入过程，较少关注主线控制措施。针对汇入区瓶颈问题，目前研究大多假定主线最外侧车道，车道与匝道车辆交互，其方法通常是协调主线最外侧车道和匝道车辆之间的间隙或采用车队形式协同［5-6］，避免间隙过小导致汇入减速或间隙过大导致浪费等低效汇入行为。而实际的快速路通常是多车道，会同时包含匝道与主线外侧车道协同汇入和主线其他车道的控制问题，后者问题同等重要但目前研究不足。

（2） CAV 环境和自动驾驶环境（autonomous vehicle， AV）环境关注多，车联网环境（connected vehicles， CV）较少。一方面，受限于技术发展和安全问题，CAV 和AV 技术的成熟和大面积部署仍需要很长时间，落地应用需要较长的时间。另一方面，目前大部分研究假定全CAV 环境［7］或部分CAV 环境［8］，设计车辆轨迹优化模型，这种“硬控制”方法假设CAV车辆是完全受控，虽然这种方式可大幅提高汇入区的运行效率，但在落地应用时对路侧基础设施、通信延迟、车辆动力控制精度要求很高。

综合以上背景，本文聚焦于部分CV 环境下的汇入区瓶颈主线车辆运行优化问题，采用建议式地“软控制”，提出一种以最小化车道流量差异为目标的双向换道建议优化模型，该模型为混合整数线性规划模型，可以实时滚动计算最优解，进而提升汇入区瓶颈全局运行效率。

1 研究综述

目前国内外关于CV或CAV环境下换道建议控制已有一些研究，换道建议不仅可应用于汇入区瓶颈［9］，同时可以用于缓解高快速路下匝道［10］和车道减少区或临时车道封闭［11］等交通瓶颈的拥堵。从换道建议研究侧重点来看，可以分为换道建议最优位置选择和车道流量分布控制两种。从控制方法论来看，现有研究可以分为三类：①基于规则策略的控制；②反馈控制方法；③优化模型控制方法。第一类中，Mehr等［11］通过计算车辆在到达车道封闭终点前成功换道的概率，在此概率低于一个阈值之前进行提前换道建议；类似的，He 等［12］通过IDM（intelligent driver model)跟驰模型、MOBIL 换道模型和换道间隙接受模型进行微观交通流建模，通过数值仿真确定最佳的换道建议位置；Nagalur等［13］综合考虑各车道流量分布及其通行能力，通过解析式计算的方法设计CAV 车辆的多种车道分配策略，Zhang 等［14］针对可变限速控制不能充分解决瓶颈区失效的问题，组合设计了可变限速控制和换道建议方法，该换道建议方法包含了与换道位置和换到空间长度相关的5 条规则。第二类中，Roncoli 等［15］依据车道均衡原则，设计了一种线性二次调节器反馈控制方法，追踪交通流的临界密度从而提高瓶颈区域的通过量，并进一步考虑了特殊管控需求下（如靠右行驶、内侧车道只能超车等）的车道流量不均衡情况下的反馈控制［16］；Markantonakis 等［17］则分别对主线的可变限速控制和换道建议控制设计了两组线性反馈控制器；Tajdari 等［18］结合了传统的匝道信号控制和主线的换道建议控制，同时考虑了所涉及的反馈控制的的闭环系统稳定性问题，仿真测试表明该方法显著优于经典匝道控制方法；第三类中，Gong等［19］研究了快速路下匝道的最优换道建议位置点，将下匝道上游分为绿色的可安全顺畅换道区和黄色的需要减速才能换道区域，通过建立优化模型最小化强制换道导致的延误寻找绿色区域的起始点，即最优换道建议点；Subraveti 等［20］基于一阶宏观交通流模型量化延误，建立优化模型最小化总行程时间，此研究更关注宏观的横向流量控制，并未给出具体的基于个体车辆的换道建议；Ramezani 等［21］提出双层换道建议方法优化瓶颈区车道密度分布，上层通过交通流基本图确定最优密度决定每个车道需要换道的车辆数，下层则是综合考虑匝道汇入车辆和主线车辆的冲突给出换道建议。总体来说，基于规则策略的换道建议控制方法对交通流的微观建模考虑较少；反馈控制方法通常需有控制设定数值（大多为交通流临界密度），在此基础上进行反馈调节，这个数值的寻优也是一个问题；优化模型方法相对来说可以灵活处理各种交通流输入条件，且合理的目标函数设定可以保证控制效果。

本文立足于换道建议控制中车道流量分布问题，针对以往基于优化的换道建议模型需要依赖交通流基本图而导致的不准确和大部分只能进行单向换道建议的问题，提出一种可以双向换道建议的混合整数线性规划模型，该方法不依赖于交通流基本图设定的临界密度，通过最小化车道间流量的差异平衡各车道流量，微观交通仿真软件测试结果表明，该方法可以有效减小快速路汇入区瓶颈的车均延误。

2 换道建议优化模型

换道建议控制的基本原理是通过给CV发送换道建议解决汇入区各车道流量不均衡的问题。通常匝道车辆汇入导致主线外侧车道拥堵，部分主线外侧车道车辆向更内侧车道转移，拥堵向内蔓延，导致汇入区整体失效，频繁换道导致车辆减速且延误增加。CV换道建议算法通过让部分CV在汇入点更上游处提前换道，使汇入区附近车辆间的交互冲突分散在更大的范围，由于外侧车道已经腾出间隙，主线车辆与匝道车辆的冲突减少。在另一种情况中，主线车辆可能为了避让匝道车辆大量分布在内侧车道，此时CV换道建议算法会建议部分内侧车道车辆转移至外侧车道。尽管本研究的换道建议会在汇入点上游引入新的冲突，但这种冲突程度相比于汇入冲突集中于下游的情况更小，由于在优化模型中引入上游冲突会使得模型高度非线性且求解不稳定，本文暂不考虑上游交通流换道建议带来的新的换道冲突。整体来说，本模型通过平衡个车道流量且分散汇入冲突从而提高整个汇入区的运行效率。图1为汇入区换道建议示意图。

图1 汇入区换道建议示意图Fig. 1 Schematic of lane changing advisory at a merging area

如图1所示，以主线为N车道的汇入区（此处以主线4车道匝道1车道为例，车道编号以最外侧即路肩侧为1，向内依次增加），假定车流中有一定渗透率的CV车辆，路侧有通信与计算中心，该中心能够感知各个车道的实时车辆数，并收集CV 车辆的位置信息，每隔一定时间通过计算换道建议优化模型得出每一辆CV应该向左、向右或者保持当前车道，并将换道建议结果发送至相应的CV 车辆。换道建议优化模型变量说明如表1所示。

表1 换道建议优化模型变量Tab. 1 Variables in lane changing advisory optimization model

目标函数：

约束条件：

该模型中，控制变量是 ri，j和 li，j，即每一辆CV是否需要向左变道或向右变道，状态变量是每一个车道内的当前车辆数和CV 变道后的每个车道内的（预期）车辆数，目标函数（1）则是CV变道后每个车道内的最大车辆数与最小车辆数之差，这个目标函数可以平衡各个车道的车辆数。约束条件（2）是最外侧车道的车辆不能向右变道，约束条件（3）是最内侧车道车辆不能向左变道，约束条件（4）是只能有一个换道建议（向左、向右或保持当前车道），约束条件（5）是计算所有车辆执行换道后每个车道的（预期）车辆数，约束条件（6）是CV 换道后的最大车道车辆数，约束条件（7）是CV 换道后的最大车道车辆数，约束条件（6）和（7）的引入可以避免优化模型中出现取最大值和取最小值运算，保持整个模型的线性。

整个CV 换道建议模型是一个混合整数线性规划模型（mixed integer linear programming， MILP），对于MILP，典型的商业求解器（如IBM CPLEX，GUROBI， FICO， MOSEK）和开源求解器（如SCIP， GLPK， LP_Solver， CMIP）均可以较快求解。此研究中的MILP 模型规模不大，采用最快的开源求解器SCIP［22］即可。测试表明，假定匝道车辆数为15，主线4个车道各有20辆车，在CV渗透率为100 %时（渗透率越大，计算开销越大），在普通的Intel（R） Core （TM） i7-6700 CPU @3.40GHz 处理器计算下，模型求解速度为0.018 s，因此CV换道建议算法可以满足实时性要求。

3 仿真评估平台与场景设计

3.1 仿真平台框架

为了综合评测以上提出的汇入区换道建议控制算法，本研究使用VISSIM 7.0版本作为仿真测试平台，VISSIM COM结合Python程序设计语言构成的测试平台框架如图2 所示。其信息流的传递过程为：首先VISSIM 路网中的交通流信息通过VISSIM COM传递到Python环境，然后这些信息作为优化模型的参数输入进入SCIP 的官方求解包Pyscipopt，优化结果存储在数据库控制表，控制指令一方面通过VISSIM COM传递回路网执行，另一方面保存成轨迹用于最终的结果评估。

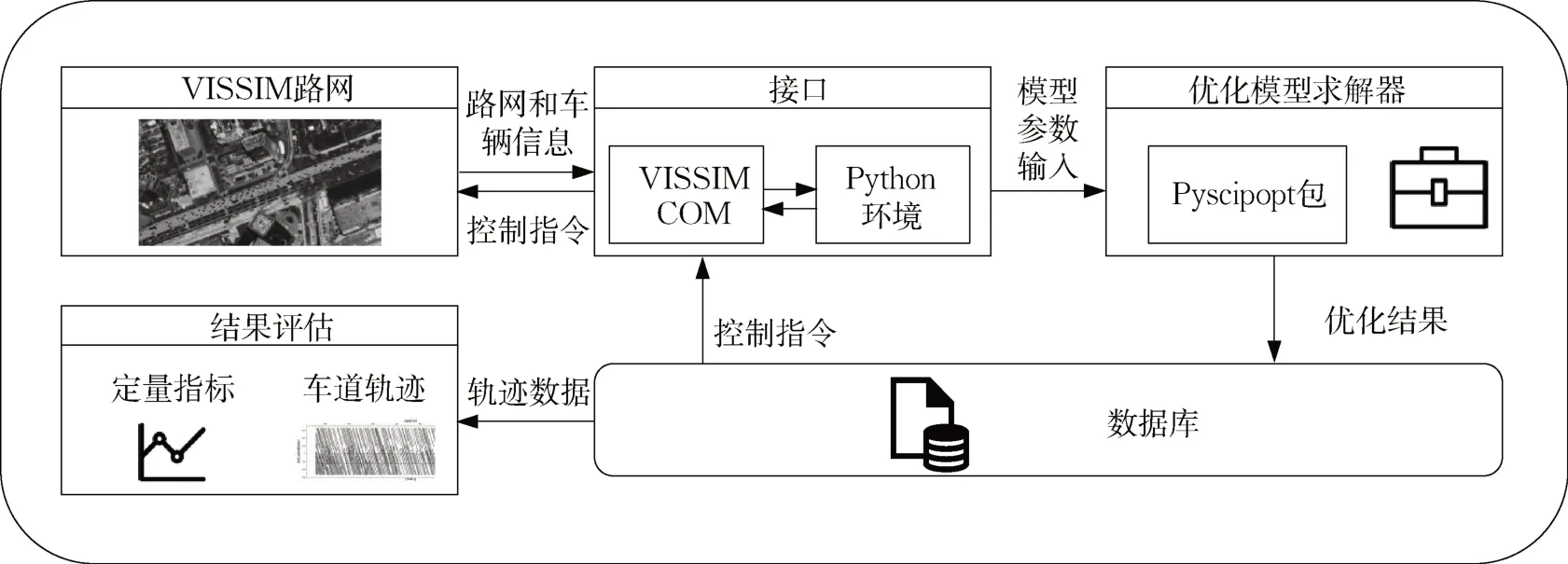
图2 基于VISSIM和Python的仿真测评平台框架Fig. 2 Framework of simulation and evaluation platform based on VISSIM and Python

3.2 仿真评估实现

基于上海市中环国和路上匝道卫星云图，建立汇入区VISSIM路网，如图3所示。该汇入区主线有4 车道，匝道有1 车道，汇入区总长度约为610 m，上匝道长度约为250 m，道路限速为80 km·h-1。VISSIM 软件驾驶行为设定为类型3（即快速路，自由选择车道），车辆组成为默认的98 %小型车和2 %大型车。由于默认的VISSIM 驾驶行为参数在多车道汇入区仿真中会出现主线车道车辆速度过大、匝道汇入车辆无法汇入进而排队等现象，因此需要对驾驶行为类型3 中的换道行为参数微调，在设定中勾选协同换道，同时适当减小安全距离减小系数，本文中这个数值设定为0.35。对于CV的模拟，在小汽车驾驶人模型的基础上新建一种车辆类型作为CV，这些CV 与普通的VISSIM 内部小汽车驾驶行为没有区别。此外，不同CV 的渗透率通过交通组成比例模拟。

图3 上海中环国和路汇入区瓶颈Fig. 3 On-ramp bottleneck on Guohe Road of Shanghai Middle Ring Road

本文设定3 个场景变量综合评估CV 换道建议优化模型：①控制方案，包含无控制和CV换道建议控制两种方案；②交通流量组合，其中匝道4种流量为900，1 200，1 500，1 800 veh·h-1，主线4 种流量水平4 700，5 200，5 700，6 200 veh·h-1，因此共构成16种交通流量组合；③CV 渗透率，即0.1～0.9 范围内以0.1递增，共9种水平。16种交通流量组合水平从单车道1 400 veh·h-1的低流量到过饱和的2 000 veh·h-1，范围较广，可以测试本文提出方法的流量适用范围。

具体仿真流程如图4 所示，首先Python 通过调用VISSIM COM 启动仿真程序，提取VISSIM 静态信息的提取（路径、路段长度等）用于VISSIM 内部坐标（所在路段和路段内局部坐标）和全局一维坐标（其中匝道与主线交点处全局坐标为0）的转换，接着进入单场景的仿真测评，设定主线和匝道的交通流量、CV渗透率等参数，随后仿真预热480 s。进入仿真步长为0.2 s的单步仿真阶段后，如果是原方案则不作任何控制，直接在每一个仿真步长末提取当前时刻所有车辆的相关信息（路径、路段、位置、速度等），并保存全局坐标下的轨迹；如果是CV 换道建议方案且到达计算间隔，则提取动态的交通流信息，即当前时刻换道建议区内各车道的实时总车辆数和CV 车辆信息，在本研究案例中，换道建议区的范围是汇入点上游200 m到汇入点之间。其后动态交通流信息输入换道建议优化模型，在Python 中调用SCIP 的官方包Pyscipopt，实时求解MILP 换道建议模型，并将结果通过VISSIM COM 接口返回到VISSIM路网中，设定相应的CV车辆的期望车道和绿色颜色标识，最终VISSIM单步仿真执行CV换道建议算法的优化结果。为了防止车速过低的换道对主线交通效率产生严重影响，本文控制换道建议时，如果车辆速度低于3 m·s-1则取消此次换道建议。此外，该换道建议算法每隔一个固定的时间计算一次，如果这个时间太短，驾驶员可能来不及反应，接受度会降低，如果时间太长，则换道建议算法跟不上汇入区内各车道的实时车辆数，控制效果变差，本文中这个控制步长取5 s。仿真达到4 200 s后结束，进入评估阶段，利用保存的车辆轨迹数据（从600 s 到4 200 s期间的轨迹数据用于评估），可视化各车道所有车辆的轨迹，同时计算该场景下的车均延误，最后进入下一个场景并重复前述过程。

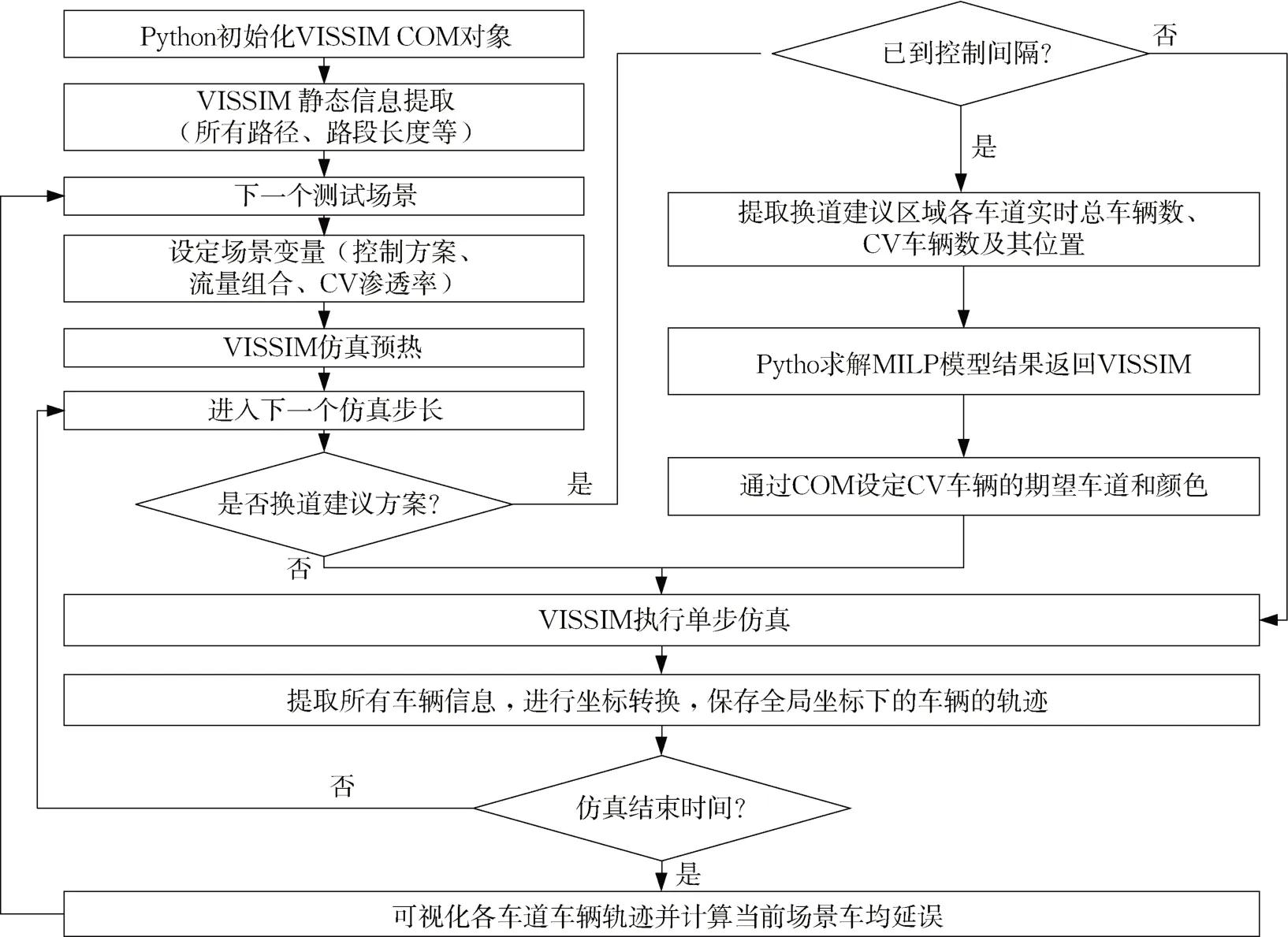
图4 仿真测试实现流程图Fig. 4 Flowchart of simulation test

4 模型效果评价

模型效果评价从三方面考虑，其一是定性的轨迹与流量评价，其二是通过计算车均延误进行定量评价，最后进行敏感性分析研究CV 渗透率对换道建议控制算法的影响。

4.1 轨迹与流量评价

图5 和图6 分别展示了主线5 200 veh·h-1匝道1 800 veh·h-1流量下原方案和换道建议控制方案的各车道轨迹，时间范围为600～1 000 s，其中换道建议方案轨迹中CV渗透率为0.5。其中车道1部分是主线最外侧车道和匝道车道的车辆轨迹，车道2/3/4部分分别是从外到内的3个内侧车道轨迹。

图5 原方案各车道轨迹Fig. 5 Trajectories of original scheme

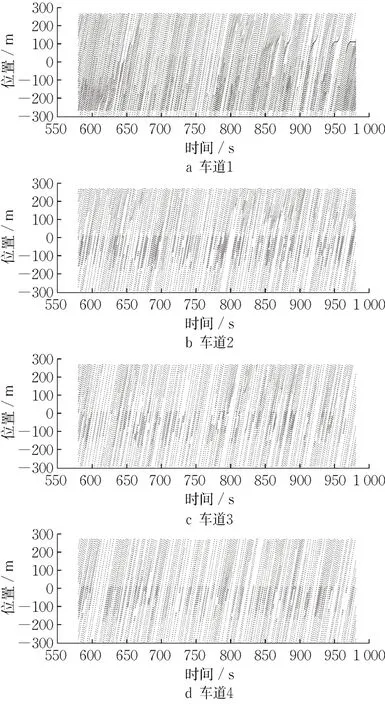
图6 换道建议方案各车道轨迹Fig. 6 Trajectories of lane changing advisory control scheme

在原方案中，从内到外各车道交通状态逐渐恶化，车道4受到的汇入冲突影响小，所有车辆均很少减速，迅速通过汇入区，车道3 略微受到影响，车辆有一定程度减速，车道2 由于车道1 的车辆横向转移，又较明显减速，车道1由于直接有大量匝道车辆汇入，冲突多，车辆明显减速甚至停车排队，因而延误大，同时车道1 通过的车辆数也较多。原方案轨迹示意图充分显示了汇入区因外侧车道流量过饱和而带来的失效，这也是使用CV 环境对汇入区进行换道建议控制的基本出发点。

作为对比，在CV换道建议算法控制下轨迹图中，其中加粗圆点部分的轨迹代表正在执行换道建议控制（注意，保持当前车道也算是一种控制），在算法的影响下，最外侧车道大量车提前向内侧车道转移，减小了匝道汇入车辆与主线外侧车辆的冲突，车道1车辆数明显减小，很少车辆大范围减速。车道2/3的部分车辆也提前向内侧转移，冲突分布广泛，因此减速也不明显，车道4相比原方案也是略微提升。

为具体评估车道流量分布情况，本文避免仅对某一空间点流量进行采集，因为拥堵发生的空间不均匀性会导致评估出现偏差。本文采用Edie’s交通流参数定义，其中流量定义为交通流中所有车辆在特定的时间和空间范围内所行使的总里程（单位为m），在评估过程中将流量分为总流量、上游流量和下游流量。其中总流量时空范围包括了所有评估时间的所有路段上的轨迹，上下游流量统计则以汇入点（全局坐标0）作为分界线，各车道总流量和上下游流量如表2所示。可以看到，主线外侧车道（编号1）的流量明显高于其他车道，相比于控制前，控制后的车道1 总流量明显减少，并部分转移至内侧车道。观察车道1 减小的流量，可以发现主要来源于上游流量的减少，这些流量转移至2/3/4 车道可以使上游的流量相对均衡。

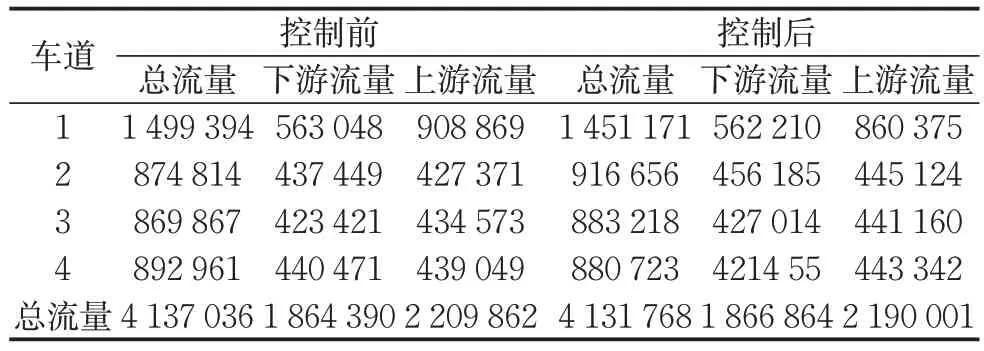
表2 基于Edie’s定义的交通流量车道分布Tab. 2 Traffic flow lane distribution based on Edie’s definition

总体来说，CV换道建议算法减小了汇入区各车道的流量差异，使得汇入导致的冲突不再集中于加速车道附近区域，匝道汇入车辆减速现象明显变少，内侧车道交通流也无恶化现象。尽管如此，汇入区的总体车均延误是增加还是减小，仍然需要做定量评估。

4.2 车均延误评价

本文定量评估指标为车均延误，定义为：

表3 总体车均延误对比Tab. 3 Comparison of overall average vehicle delays

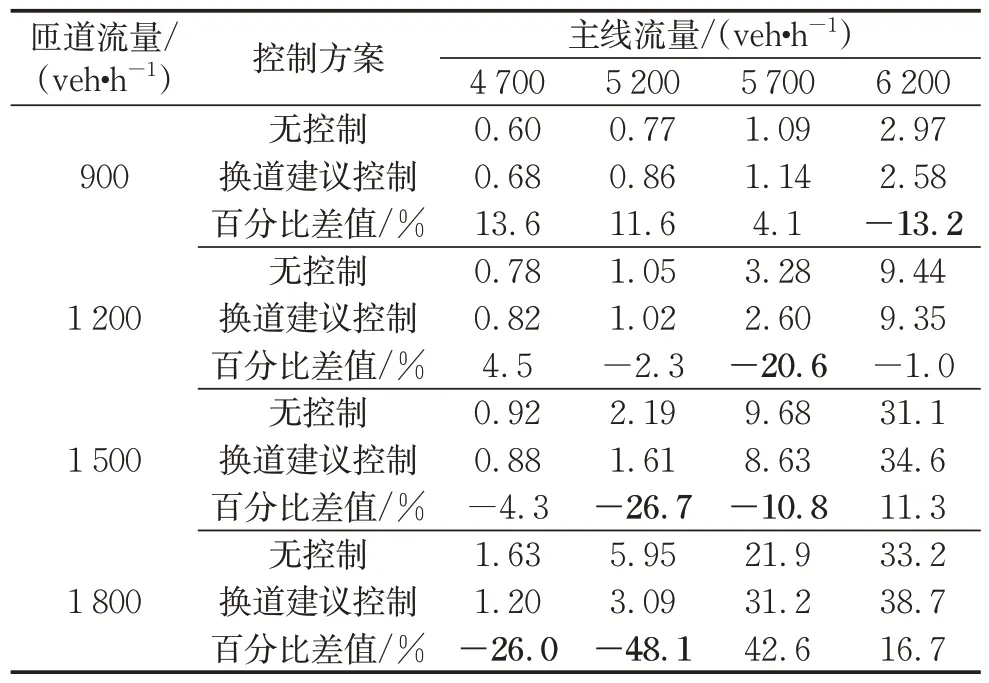
表4 主线车辆车均延误对比Tab. 4 Comparison of mainline average vehicle delays

在各个表中，换道建议方案相比原方案车均延误降低5 %以上的数值标为粗体，这些场景可以认为有明显的正优化改善效果。对匝道车辆来说，只要汇入区没有完全过饱和，在中低或中高流量下车均延误均有明显改善，而对于主线车辆车辆来说，流量过低或过高时换道建议都会造成一定的延误增加。

从总体角度考虑，考察表3可以发现，有正优化的场景集中分布在对角线处，这些场景的总流量范围在6 200 ～7 200 veh·h-1之间（即单车道平均流量1 550 ～1 800 veh·h-1），属于匝道汇入区瓶颈临界失效流量区间，而左上角低流量水平和右下角过饱和流量水平场景中，换道建议反而会使得车均延误一定程度增加。原因为：（1）流量过低时，主线各车道交通流原本就很通畅，外侧车道并未发生明显拥堵，换道建议对主线外侧车道改善本身就不明显，反而在内侧车道引入额外冲突增加主线车辆延误，尽管匝道车辆车均延误有一定降低，总体车均延误还是有一定幅度的增加；（2）流量处于过饱和水平时，此时汇入区已经失效，即使外侧车道已经腾出间隙，也不能大面积减小汇入冲突导致的延误，同时内侧车道的车辆本身速度已经很低，大量换道建议带来的减速交通波不断传播向上游，因此总体延误大幅度增加。综合来看，换道建议方案有其特定的适用流量范围，中高流量水平控制效果较好，原因是此时汇入区处于失效临界状态，一旦冲突过大汇入区随时会失效，但恰当的控制却可以避免失效，同时降低主线和匝道汇入车辆的延误。

另一方面，表3 结果还表明当主线流量不高但匝道流量较高时，换道建议方案对车均延误的减少幅度最大。最佳的延误变化百分比出现在主线流量5 200 veh·h-1、匝道流量1 800 veh·h-1的场景，车均延误降低可以达到48 %，其原因是匝道流量高时，原方案匝道车辆大量汇入会使汇入区迅速失效，而换道建议方案中，主线流量不高使得换道建议影响较小，同时外侧车道让出的间隙可大大减小汇入冲突。

4.3 CV渗透率敏感性分析

进一步，本文对不同CV渗透率下换道建议前后的车均延误变化百分比做了敏感性分析，即计算同一CV渗透率下，所有不同流量方案的延误变化百分比并取平均值，其结果如图7所示。结果表明，CV渗透率小于0.5时，换道建议方案对汇入区延误的改善随着渗透率提高而提高；CV渗透率大于0.5时，延误变化百分比无明显变化，说明过高的CV渗透率不是必要的。综上，本文提出的换道建议方案在CV渗透率在0.2～0.5时，即可达到较好的降低汇入区延误效果。

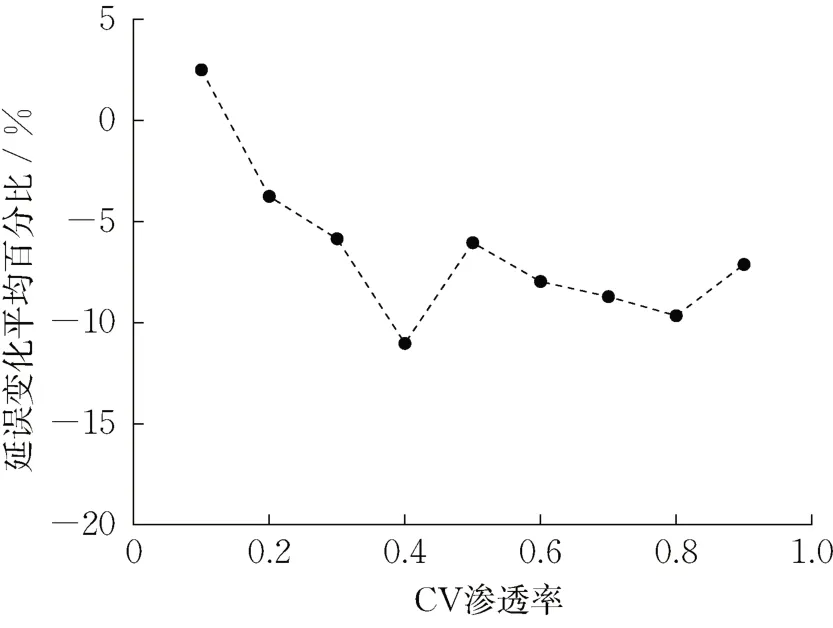
图7 不同渗透率下换道建议前后延误变化平均百分比Fig. 7 Percent change of delay before and after CV lane changing advisory

5 结语

本文旨在解决多车道汇入区各车道流量分布不均导致的汇入区运行效率降低问题，借助车联网环境提出一种换道建议算法以降低汇入区的车均延误，并通过仿真软件二次开发对模型进行了系统的实验测试，主要贡献和结论总结如下：

（1）聚焦汇入点上游主线车辆的换道行为，采用建议式地“软控制”方法，提出一种基于优化模型的精确到个体车辆的换道建议方法，输入条件为汇入区各车道的车辆数，目标函数为最小化各车道车辆数差异，该模型为混合整数线性规划模型，可以实时滚动计算最优解；

（2）在VISSIM 交通仿真软件中测试了不同流量组合下算法的有效性，定性轨迹和定量车均延误结果表明在单车道平均流量1 550～1 800 veh·h-1区间（汇入瓶颈失效关键流量区间）下换道建议方案相比原方案能显著改善汇入区的运行效率，车均延误可降低10 %～50 %左右；且在此范围内，匝道汇入流量越高，改善效果越好；

（3）对不同CV渗透率敏感性分析结果表明在较低的0.2～0.5渗透率下即可达到减小延误的目的。

作者贡献声明：

胡祥旺：研究框架制定，模型提出与验证，论文写作和修改。

倪颖：研究框架制定，研究指导，论文修改。

孙剑：研究框架制定，研究指导，论文投稿与修改。