基于优化VMD与GRU的混凝土坝变形预测模型
张建中,顾冲时,袁冬阳,王岩博
(1.河海大学水灾害防御全国重点实验室,江苏 南京 210098; 2.河海大学水利水电学院,江苏 南京 210098)
我国已修建水库大坝近10万座,其不仅发挥了防洪、发电、供水、航运等综合效益,而且对调控水资源时空分布、助力能源结构低碳转型、促进国民经济发展等具有重大意义。在运行期间,水库大坝长期服役安全存在很多风险隐患,再加上一些工程设计和历史遗留等问题,很多工程都面临着安全隐患,一旦失事,将会对下游人民的生命财产安全和水生态安全造成巨大的威胁[1-2]。安全监测是保证混凝土坝长效服役安全的重要手段[3-5]。变形作为最能直观反映混凝土坝在外部荷载和内部荷载耦合作用下运行性态的监测效应量,是安全监测的重点[6-7]。使用混凝土坝变形监测数据进行合理的变形行为分析及预测,对保障混凝土坝长效服役安全、实时诊断大坝健康态势与预测未来运行行为具有重要意义[3,8]。
混凝土坝变形监测数据是一种非线性、非稳态特征的时间序列,使用信号分解理论可将其分离成不同频率信号序列[9-11]。为提高预测精度,通过引入“分解-重构”的思想,将监测数据进行高低频分解,分解成不同频率的子序列,然后分别进行预测、重构[12-13]。朱宝强等[14]依据时间序列原理将混凝土坝位移序列分解为趋势项与随机项,并用改进的支持向量机(support vector machine,SVM)进行预测;陈俊风等[15]使用小波分解把原始序列分解成多个子序列,用优化的BP神经网络分别对这些子序列进行预测;徐肖遥等[16]使用经验模态分解(empirical mode decomposition,EMD)将变形数据分解成多尺度变形分量,结合改进的极限学习机(extreme learning machine,ELM)对变形分量进行预测;马佳佳等[17]运用集合经验模态分解(ensemble empirical mode decomposition,EEMD)将原始数据分解为不同频率分量,然后分别使用长短期记忆神经网络(long short term memory neural network,LSTM)和多元线性回归对高频和低频分量进行预测;王飞等[18]采用局部均值分解将变形数据分解成趋势项和随机项,结合相关向量机和整合移动平均自回归模型进行组合预测;张健飞等[19]使用变分模态分解(variational mode decomposition,VMD)将变形时间序列数据分解成一系列模态分量,采用卷积神经网络对各模态分量建模并预测。
相比于单一方法(如BP[20]、ELM[16]、SVM[21]等)的变形预测模型,以上“分解-重构”变形预测模型具有更好的性能,但其分解及预测方法对模型预测性能有着很大的影响[19-22]。就位移序列分解方法而言,小波分析分解彻底,但自适应能力不强,分解尺度选取困难,很难获得最优解[23-24];经验模态分解自适应性强,时频分辨率高,但存在模态混叠等问题[25];EEMD虽能抑制模态混叠现象,但分解个数随机不可控,需要多次迭代求均值[26];局部均值分解可缓解端点效应,但在模态混叠方面仍需改进[27];相比EMD和EEMD等分解方法,VMD拥有更好的鲁棒性,可通过信号的自适应分解,有效缓解EMD模态混叠和解决EEMD分解层数不可控等问题[21,28]。
就模型预测而言,BP神经网络具有出色的非线性特质,但收敛速度慢[20];ELM收敛速度快、泛化能力强,但模型稳定性不够理想[16];SVM拥有很好的学习能力,但模型计算速度比较慢,鲁棒性还需提高[21];整合移动平均自回归模型在时间序列上有很强的有效性,但只能预测具有线性关系的数据[18]。而混凝土坝在运行过程中产生的变形监测数据是一种时间序列,循环神经网络(recurrent neural network,RNN)是一种擅长处理各种与时间序列有关的深度学习算法[29-30]。LSTM和门控循环单元(gate recurrent unit,GRU)在RNN基础上进行改进,是两种特殊的循环神经网络,能有效解决RNN存在的梯度消失等问题,且相比LSTM,GRU具有更少的参数,其训练效率更高[31-34]。
考虑到“分解-重构”预测模型相比单一模型具有更好的预测性能,本文提出了一种基于优化VMD与GRU的混凝土坝变形预测模型,针对VMD分解参数需人为设置,参数过大或过小都会影响分解效果,GRU超参数的设置直接影响其训练速度、使用效果及鲁棒性等问题[35-36],引入一种具有结构简单、参数少、求解精度高及收敛速度快等优点的群智能优化算法(grey wolf optimization,GWO)对VMD及GRU的参数进行优化选取,并与GRU、BP神经网络、ELM及VMD-GRU等预测模型进行对比,验证该模型的可靠性与有效性。
1 模型构建
1.1 GWO优化VMD
VMD是一种非迭代、自适应且准正交的信号分解方法。该方法本质上是一种基于希尔伯特变换和混合频率变分问题的自适应维纳滤波器,可以通过循环迭代的方式,搜寻求得变分问题的最优解,基于交替方向乘子法,确定每个本征模态函数(intrinsic mode function,IMF)的中心频率和带宽,由此实现各分量从低频到高频的有效分离,从而得到信号频域的特征信息。惩罚因子α和分解模态数K是变分模态分解过程中约束带宽的重要参数,决定各模态的能量变化,其取值对最终分解效果的准确性以及后续信号处理有着至关重要的影响,目前VMD参数一般采用人为设置,对数据分解的高效性与精确性有很大的影响,且很难达到最佳分解效果。本文采用GWO对VMD的两个参数α和K进行优化取值。
排列熵可以反映出信号的复杂程度,计算排列熵可以确定位移序列分解后的复杂程度,故将排列熵作为优化VMD参数的适应度函数,排列熵越小表示VMD分解后序列越有规律,越大表示VMD分解后序列越混乱[37],故以排列熵取得最小值作为寻优目标,对参数进行优化取值。采用GWO优化VMD的步骤如下:
步骤1获取大坝原始变形监测数据。
步骤2算法参数设置。如狼群规模N、最大迭代次数tmax、参数α及K的上下限。
步骤3初始化灰狼位置向量。
步骤4计算个体适应度值。适应度函数HP的表达式如下:
(1)
式中:Pj指重构后矩阵序列出现的频率;k为j的取值上限。
步骤5将当前最优个体参数分别保存至θ、β和δ狼的位置向量中。灰狼与猎物之间的距离及第t+1代灰狼的位置向量分别如下:
Dω=|C×Xpt-Xt|
(2)
Xt+1=Xpt-A×Dω
(3)
式中:Dω为灰狼与猎物之间的距离;Xpt为第t代猎物的位置向量;Xt、Xt+1分别表示第t和第t+1代灰狼的位置向量;A、C为系数向量。
步骤6更新寻优控制因子、A和C及候选狼ω的位置向量。A、C及ω狼的位置向量表达式分别如下:
A=2a×r1-a
(4)
C=2r2
(5)
Xt+1=(X1+X2+X3)/3
(6)
式中:a为控制因子;r1、r2是模在[0,1]间的随机向量。
步骤7迭代终止条件判别。如果t 步骤8输出模型最优参数(α,K),将其代入VMD算法分解原始数据,得到优化后的IMF分量。 GRU是一种特殊类型的RNN,相比标准的RNN,GRU更完整地描述了监测效应量序列的长短期时序相关性。GRU主要由重置门和更新门组成,重置门决定信息被遗忘的程度,更新门决定上一隐藏状态传递给当前隐藏层多少信息。经过VMD分解后,各个分量的变化规律相比原始数据序列更加平稳,使用1层GRU网络神经元即可满足训练要求。隐含层隐含神经元个数n与初始学习率r是GRU网络预测过程中的重要参数,对模型构建及其预测精度有着至关重要的影响,目前GRU参数一般采用人为设置,随机性很大,很难达到最佳预测效果。本文采用GWO对GRU的n、r参数进行优化取值,以提高预测精度。 GWO优化GRU算法步骤与GWO优化VMD算法步骤基本一致,不同之处在于GWO优化GRU时采用均方误差(EMSE)作为适应度函数,以EMSE最小值作为寻优目标,即 (7) 式中:m为训练样本容量;yi为实测变形;y′i为训练得到的变形。 根据上述方法原理,优化VMD与GRU模型(以下简称“本文模型”)的主要实现过程如下:①利用GWO优化求解VMD的重要参数α及K,使用优化的VMD把原始数据分解为一组最优IMF分量;②利用GWO优化求解GRU的重要参数n及r,使用优化的GRU模型对每个IMF分量进行时序预测;③将各IMF预测结果叠加,得到位移序列预测结果。模型预测流程如图1所示。 图1 本文模型预测流程 某特高拱坝正常蓄水位1240m,总库容150亿m3,坝顶高程1245m,顶宽12m,坝体共由43个坝段组成。为掌握大坝工作性态,采用垂线法监测坝体水平位移,垂线测点具体布置情况如图2所示。为分析本文模型的有效性与合理性,取A09-PL-01、A22-IP-01和A29-IP-01共3个测点2010年7月1日至2020年2月10日的变形监测数据作为分析对象,具体监测数据如图3所示。 图2 垂线测点布置 图3 实测位移变形监测数据 为避免VMD参数随意取值影响分解效果,首先利用GWO迭代优化α和K两个参数,GWO狼群数量与最大迭代次数分别10和50,α及K的取值区间分别为[100,10000]与[2,10]。测点A09-PL-01的寻优结果为α=6071、K=8,测点分解结果如图4所示。 图4 A09-PL-01测点GWO优化VMD序列分解 测点的模态分量按从低频到高频的顺序进行排序,测点的IMF1分量是表示大坝变形趋势整体呈上升状态的趋势项;测点的IMF2~IMF5分量是周期性强、平稳强度高的周期项;测点的其余分量是周期性弱、平稳性低的随机项。 将2010年7月1日至2018年9月6日监测数据作为训练集,2018年9月7日至2020年2月17日监测数据作为测试集,以测试集的预测性能来验证模型的效果。 为避免GRU参数随意取值影响预测效果,使用GWO对GRU参数n及r进行参数寻优,以更好地捕获每个IMF的趋势进行准确预测,GWO狼群数量与最大迭代次数分别取10和50,参数n、r的取值区间分别为[2,20]与[0.001,0.02]。各个分量参数[n,r]的寻优结果分别为[7,0.017]、[13,0.016]、[20,0.011]、[8,0.010]、[17,0.009]、[11,0.011]、[6,0.020]、[14,0.011]。将优化参数代入GWO优化GRU进行预测,各分量的预测结果如图5所示。 图5 A09-PL-01测点各IMF分量GWO优化GRU预测结果 从图5可以看出,各分量的实测值和预测值的最大误差不超过0.1mm,预测误差很小。将测点所包含的各IMF分量预测结果叠加,得到测点变形预测结果。同时,为验证本文模型的有效性,同时采用GRU、BP神经网络、ELM及VMD-GRU模型等预测方法进行预测,预测结果对比如图6所示。 图6 A09-PL-01测点各模型预测结果对比 为进一步验证本文模型的普适性,对A22-IP-01和A29-IP-01两个测点进行建模预测,结果如图7所示。为评估本文模型的预测精度,综合采用决定系数(R2)、平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)作为各测点预测模型预测统计指标,计算结果如表1所示。 表1 各预测模型性能评价指标 图7 两个测点各模型预测结果对比 由图6与图7可以看出,对于A09-PL-01、A22-IP-01和A29-IP-01这3个测点,5种预测模型预测值与真实值的变化趋势基本一致,但相比BP神经网络、ELM、GRU以及VMD-GRU模型的预测结果,本文模型的预测值更加接近实测变形值,预测值和实测值基本吻合,模型具有更高的精度。由表1可知,本文模型的MAE、RMSE与MAPE均明显小于BP神经网络、ELM、GRU与VMD-GRU模型。这3个测点本文模型的R2分别为0.9996、0.9996和0.9995,显著接近于1,且明显高于其他4个模型,进一步说明了本文模型预测性能的优良性。由此可以得出,本文模型比GRU、BP神经网络、ELM以及VMD-GRU模型的预测精度更高,有效验证了该模型的普适性与稳健性。 采用GWO分别优化VMD及GRU的重要参数,避免人工赋值的不确定性,解决了模型参数选择困难的问题,提高了数据挖掘及非线性处理能力。 基于“分解-重构”的思想,将监测数据进行高低频分解,分解成不同频率的子序列,并结合深度学习网络对其预测再重构,相比单一手段建立的预测模型,预测性能更好;本文模型相比未进行参数寻优的VMD-GRU模型预测精度更高,实例进一步验证了本文模型的有效性、泛化性及准确性。1.2 GWO优化GRU
1.3 优化VMD与GRU模型预测流程
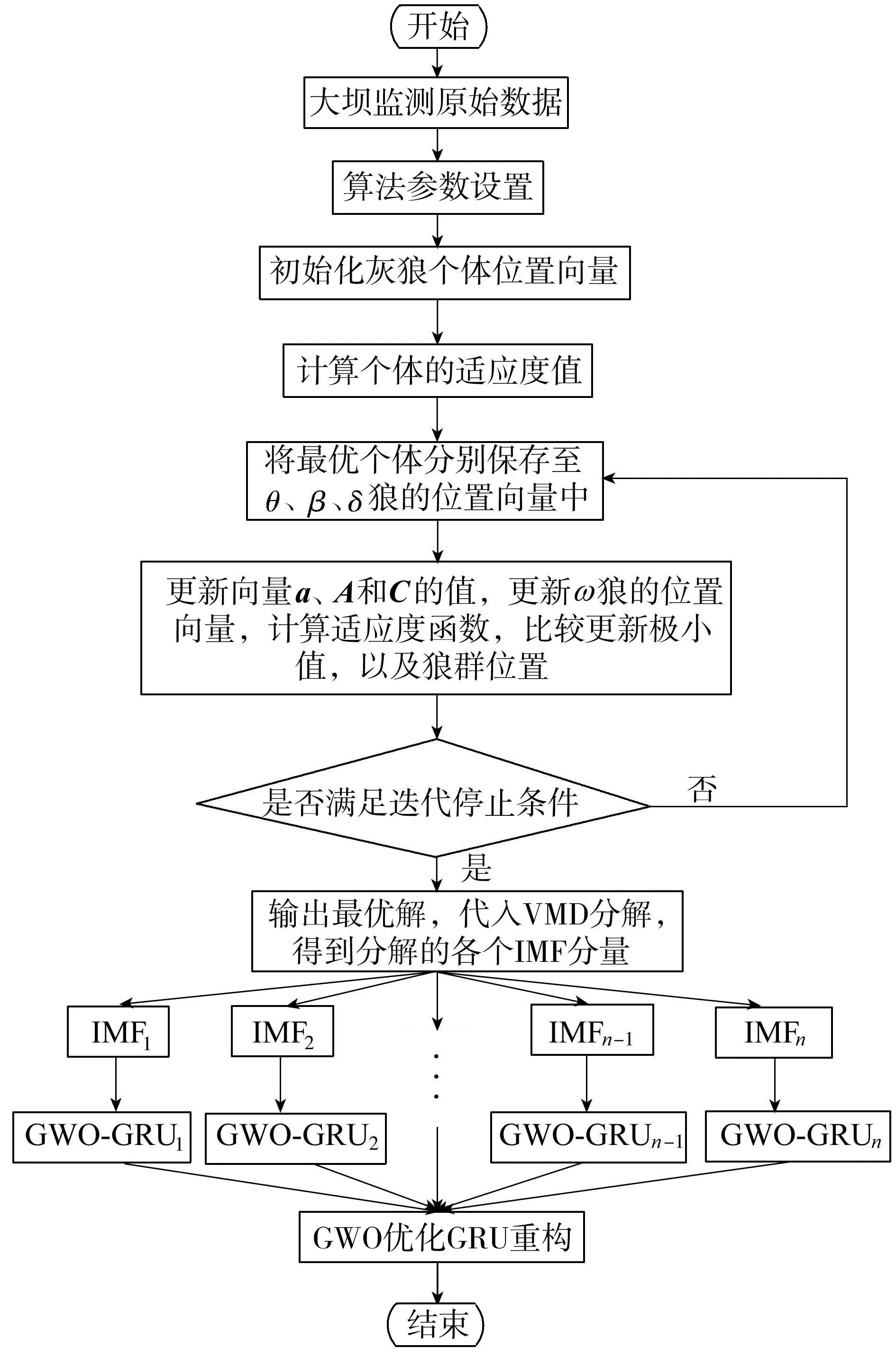
2 工程实例验证
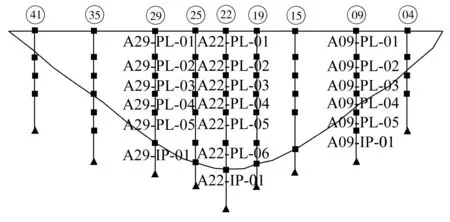
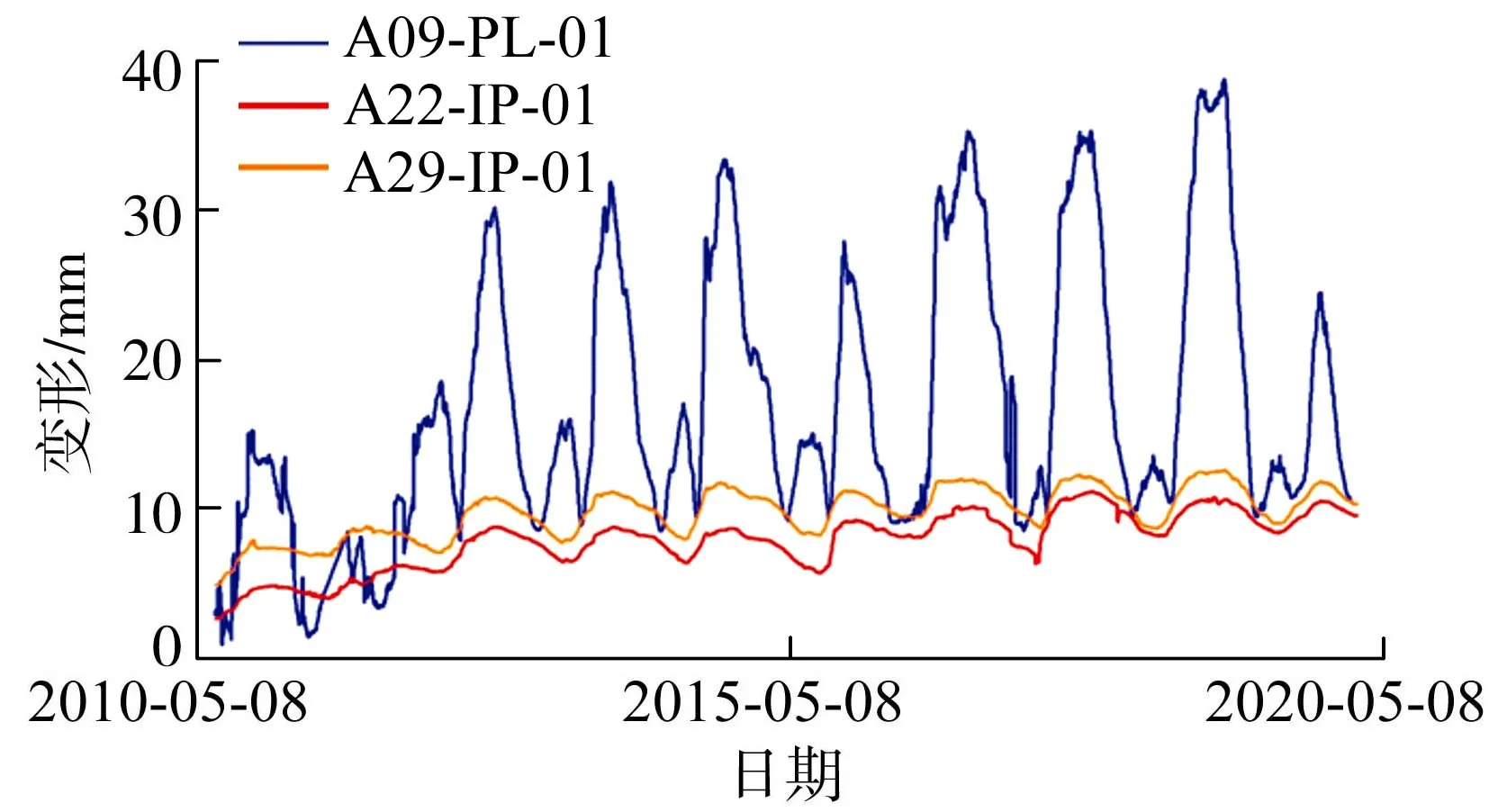
2.1 实测序列分解
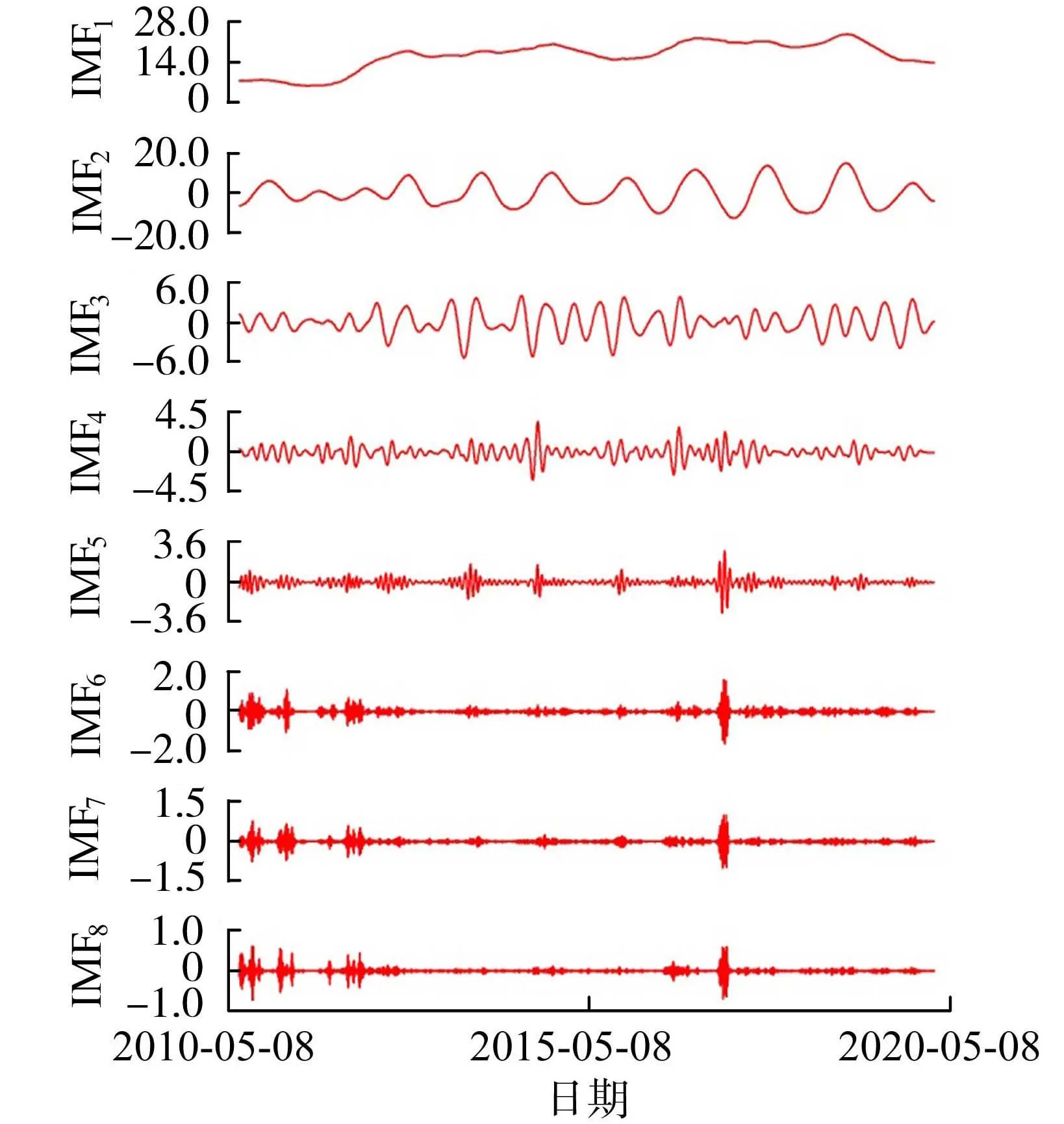
2.2 建模预测
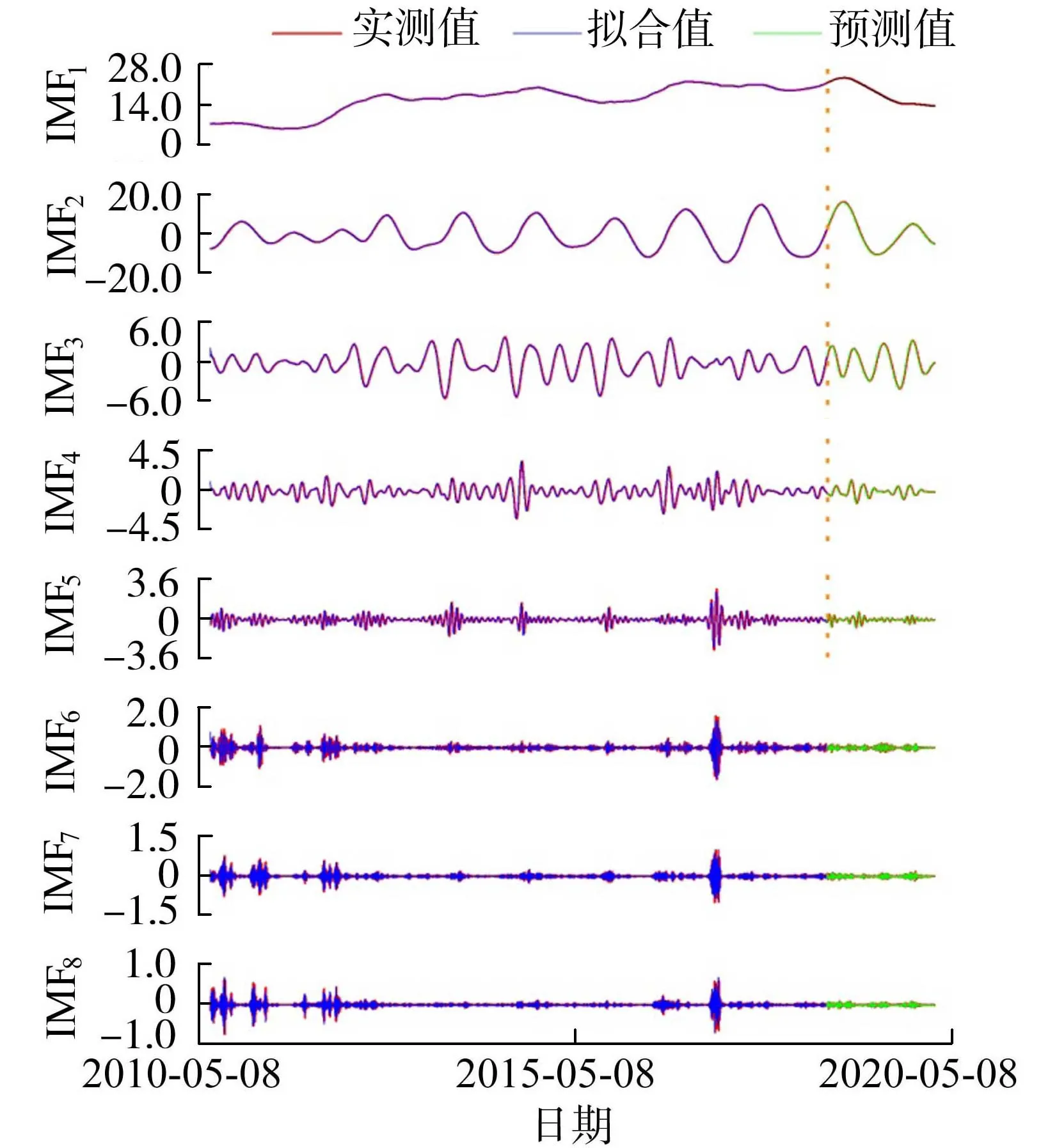
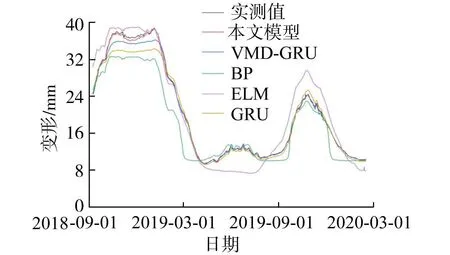
2.3 模型对比及精度分析
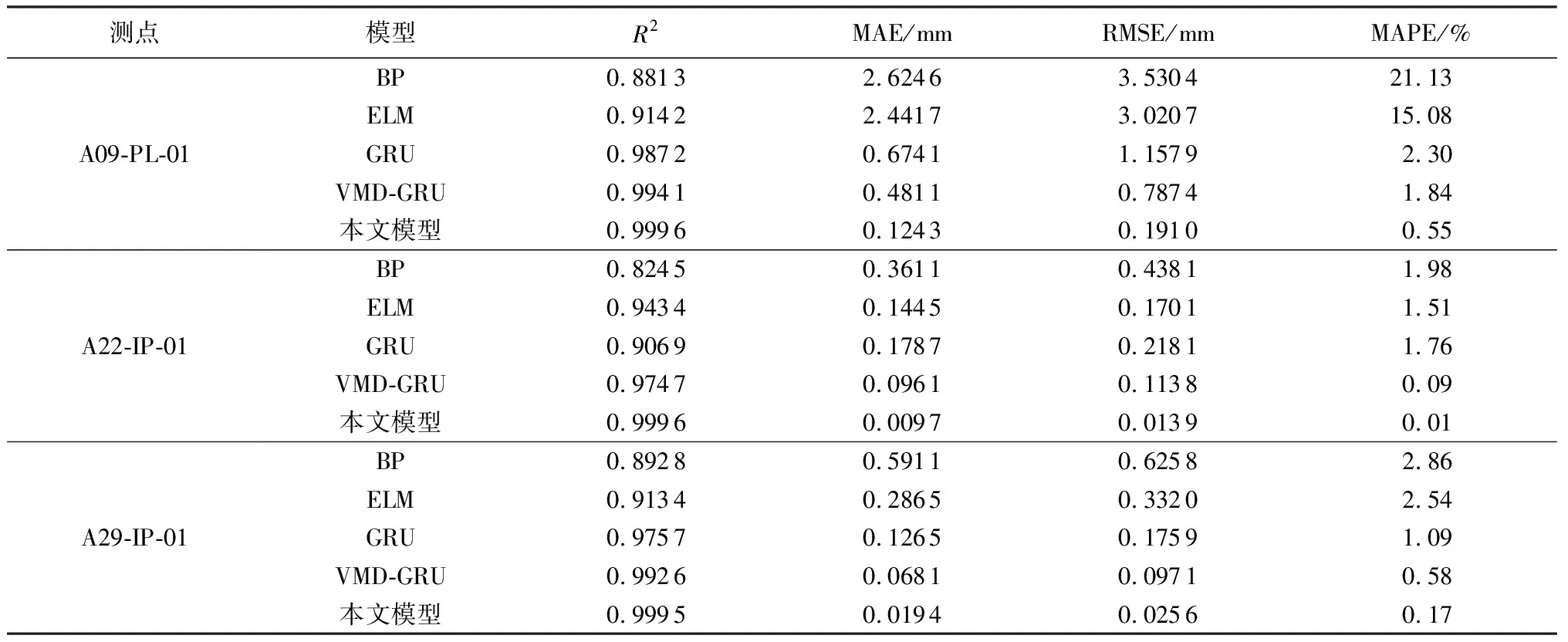
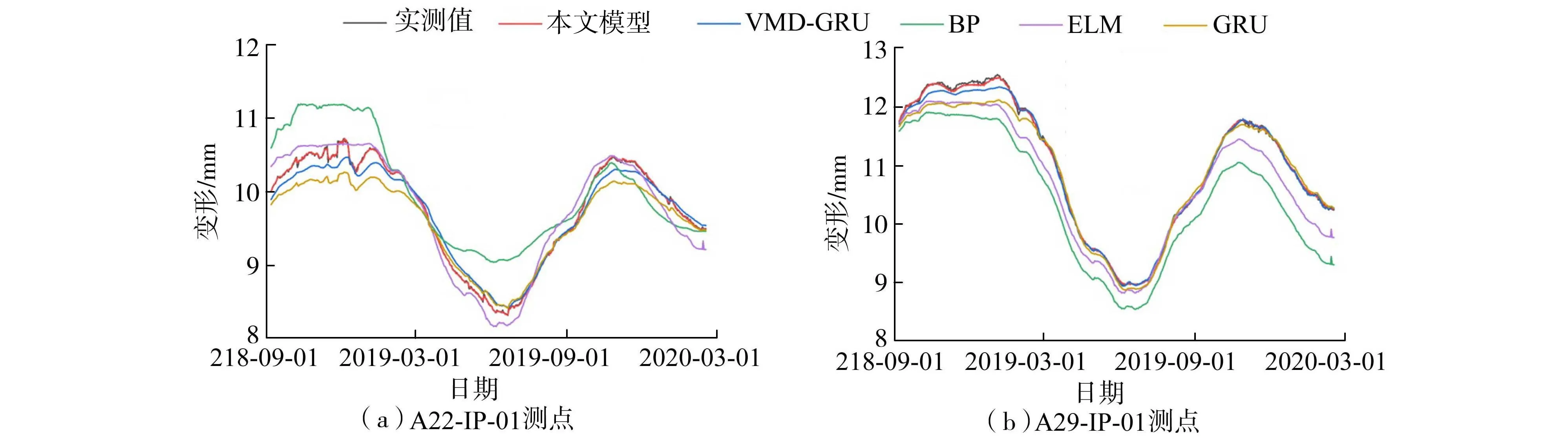
3 结 语

