基于格子玻尔兹曼方法的近壁区空化泡生长溃灭过程模拟

冉彬君,汪 磊,袁 浩,何小泷

(1.重庆交通大学航运与船舶工程学院,重庆 400074; 2.百色枢纽通航投资有限公司,广西 百色 533000;3.重庆交通大学西南水利水运工程科学研究院,重庆 400074)

空化泡初生是指当液体内部的局部压力降低或局部温度升高时,气核附近压力低于饱和蒸汽压,气核生长为空化泡。随着周边压力环境恢复,空化泡发生溃灭,在溃灭瞬间,由于短时相变引发高温高压环境,伴有强烈的冲击波和高速微射流[1-2]。这种现象常常伴随着噪声、振动和空化侵蚀,对水利水运机械的运行产生重大影响[3-4],导致设备性能下降。尽管研究者们开展了大量且系统的研究,但受限于试验观测手段、近壁区空化泡的非对称演化、宏观数值模拟中热流耦合技术的不成熟等,仍有复杂的水动力学和热动力学机理尚未被揭示。

空化泡试验研究主要基于高速摄像技术或者电火花、激光等[1,5],但由于测量技术的局限性,难以获得空化泡周边流场与温度场的连续演化过程。受输入能量、输入尺寸、边界压力等诸多因素的影响,不同研究者获得的空化泡尺寸、溃灭时间、最大流速和壁面压力均存在差异,可重复性不高。随着计算机技术的发展,计算流体力学(CFD)方法已经成为空化研究的重要工具,与试验相比,数值模拟可以实现不同条件组合甚至极端条件下空化泡的演变过程。基于玻尔兹曼动理学的格子玻尔兹曼方法(LBM)作为一种介观研究方法,是模拟多相现象的一种稳定有效的工具。与传统CFD方法相比,LBM具有计算效率高、能够处理复杂边界、可通过状态方程直接求解压力等优点[6-8]。

目前基于伪势LBM的空化模拟大多仅考虑了空化泡的溃灭过程,但初始流场调整时间往往占据着整个演化过程的1/3[9],因此流场调整带来的误差往往难以简单消除。本文利用初始输入高温激发气核,采用He等[10]构建的LBM热流耦合模型模拟了激光/电火花空化泡的初生、生长和溃灭的全过程,并着重探讨了泡壁距离和初始激发温度对流场、最大半径演化的影响,以期为深入揭示空化泡溃灭过程中的复杂规律打下基础。

1 数值模拟方法

1.1 LBM水动力模型

考虑大密度比水气多相流现象的数值稳定性,水动力部分模拟采用基于多松弛碰撞算子的LBM伪势模型,其粒子分布函数为

fi,eq(x,t))-(I-0.5Λ)SΔt

(1)

其中

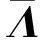
(2)

(3)

当引入非理想流体状态方程后,ψ(x)可表述为

(4)

其中

式中:cs为格子声速;pEOS为压力,本文选取Carnahan-Starling(C-S)状态方程计算:

(5)

式中:a、b、R为状态方程控制参数,a=1,b=4,R=1;T为节点对应温度。

1.2 LBM热动力模型

本文采用Li等[12]提出的LBM温度场演化计算方法以计算空化泡生长溃灭时的热动力过程,其粒子分布方程为

gi(x+eiΔt,t+Δt)=gi(x,t)-

(6)

式中:gi为用于计算温度场的粒子分布函数;gi,eq为其对应的粒子平衡态分布函数;O为源项,可表述为

O=(O0,0,0,0,0,0,0,0,0)T

(7)

其中

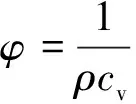
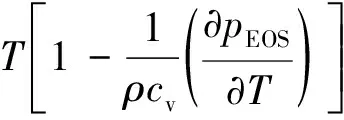
式中:φ为宏观方程中对应的修正项,其一阶和二阶偏导数采用二阶中心差分格式求解;k为热传导系数;α为热扩散系数,α=k/ρcv;cv为流体比热。本文液相热扩散系数αl取0.15,而气相热扩散系数αg取0.45,各计算点上热扩散系数取值按照线性插值求得:

(8)

式中ρg、ρl分别为气相密度和液相密度。本研究中液相比热cv_l为9.0,气相比热cv_g为3.0,各计算点上比热取值按照线性插值求得:

(9)

利用矩阵M,可以将式(6)投影到矩空间:

(10)

式中:n为gi在矩空间上的投影;neq为gi,eq在矩空间上的投影:

neq=T(1,-2,2,ux,-ux,uy,-uy,0,0)T

(11)

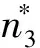
(12)

(13)

式中:τj、τq为Λ中的松弛系数;n4,neq、n6,neq为n4和n6的非平衡部分,可以通过ni,neq=(ni-ni,eq)/Δt求得。

1.3 热流耦合过程

前人研究空化泡溃灭时的热动力过程多采用被动标量法[11],并未考虑热动力过程对流场的影响。研究[8]表明,空化泡的演化伴随着温度的改变,其中表面张力随着温度的升高而降低,将直接影响空化泡的演化形态。因此本文考虑了温度场与流场的耦合,采用t时刻的宏观密度ρ(x,t)和流速u(x,t)求解t时刻温度场中的平衡态分布函数neq(x,t),进而得到t时刻的温度T(x,t);而下一时刻的压力pEOS(x,t+Δt)和伪势ψ(x,t+Δt)则采用求解T(x,t),进而得到下一步的宏观密度ρ(x,t+Δt)与流场u(x,t+Δt)。值得注意的是,本文分析均采用格子单位,其中长度单位为lu,质量单位为mu,时间单位为ts,温度单位为tu。

2 模型验证

模型验证采用无限域内单空化泡的初生和溃灭过程,并与模型试验和Rayleigh-Plesset(R-P)方程的理论解进行定性与定量对比。考虑热效应的二维R-P方程[13]可描述为

(14)

其中

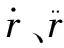
式(14)可通过四阶Runge-Kutta法求解,其中每一步的气相压力为对应的LBM计算获得的空化泡内平均压力。计算域初始激发温度场为

(15)

式中:Tl为初始液相温度;Tv为初始气相温度;(x0,y0)为初始高温中心;r0为初始圆形高温区域半径;s为高温到低温区域过渡距离。

计算域中心初始化一个半径r0=5lu、温度Tv=Tc的高温区域。通过高温区域瞬间汽化产生气核。初始边界压力和计算域内液相压力设置为pl=-2.18×10-2mu/(lu·ts2),边界压力则设置为时间函数,如图1所示。当边界压力低于平衡态压力时,空化泡处于生长过程,而当边界压力高于空化泡内压力时,空化泡则处于溃灭过程。此外采用无量纲时间t*=t/tc对比LBM模拟结果与试验结果,其中tc为空化泡溃灭时间。

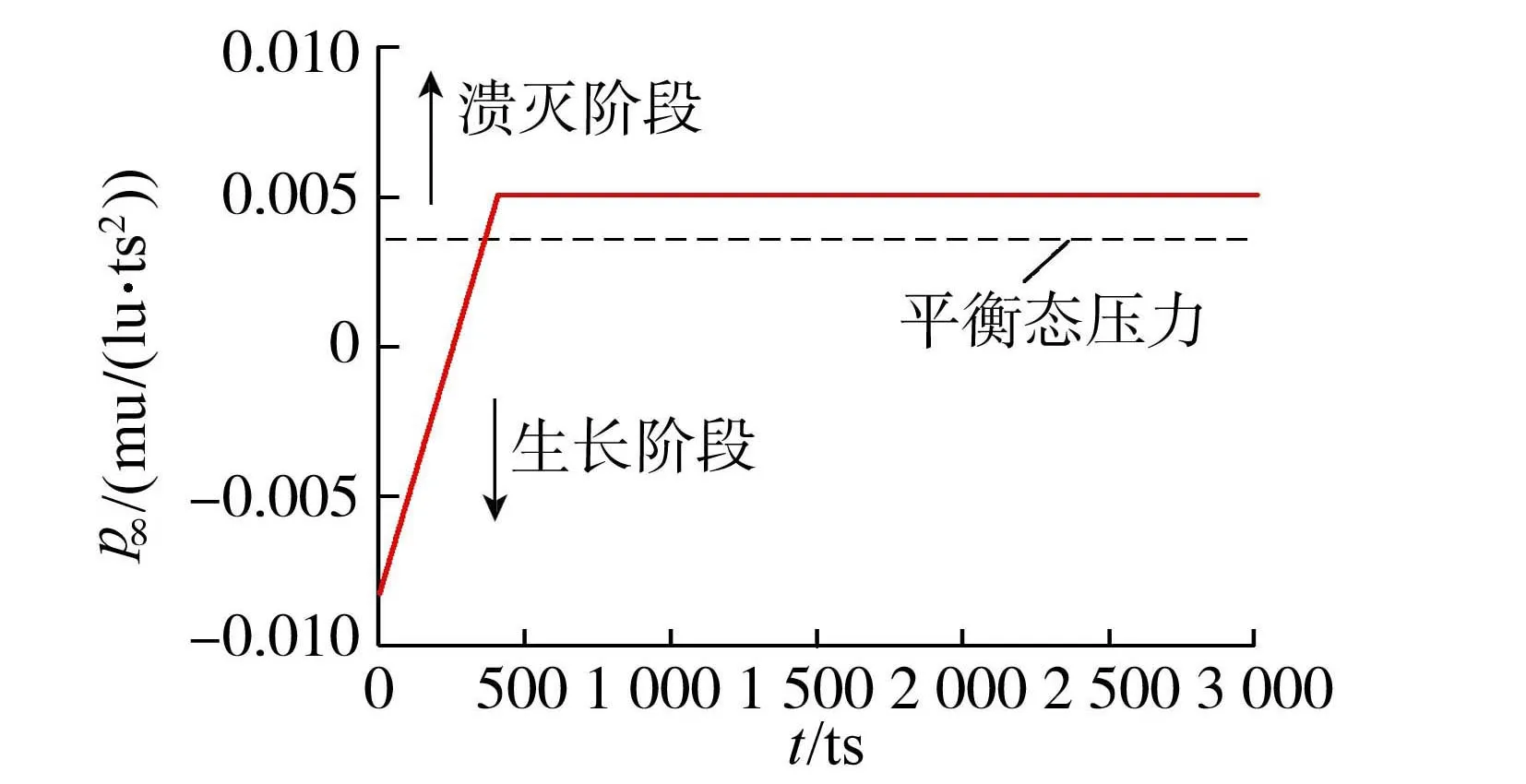
图1 边界压力随时间演化过程

LBM模拟结果与试验结果[14]中对应的无量纲时间的空化泡半径与最大半径比如表1所示,模拟结果表明空化泡在生长和演化过程中均保持圆形,两者演化过程中的无量纲半径比例接近。此外,模拟结果显示在空化泡生长过程中,主要发生液相向气相方向的相变,伴随着吸热过程,导致空化泡内温度低于周边液体;而在溃灭过程中,随着液体周边压力大于气泡内压力,主要发生气相向液相方向的相变,并伴随着放热,空化泡内温度逐渐升高。

图2为LBM模拟结果与R-P理论方程获得的空化泡半径演化过程的对比,结果表明两者吻合良好,仅在空化泡初生阶段出现较小误差,这可能是由于在LBM模拟中初始阶段流场和温度场的调整导致。

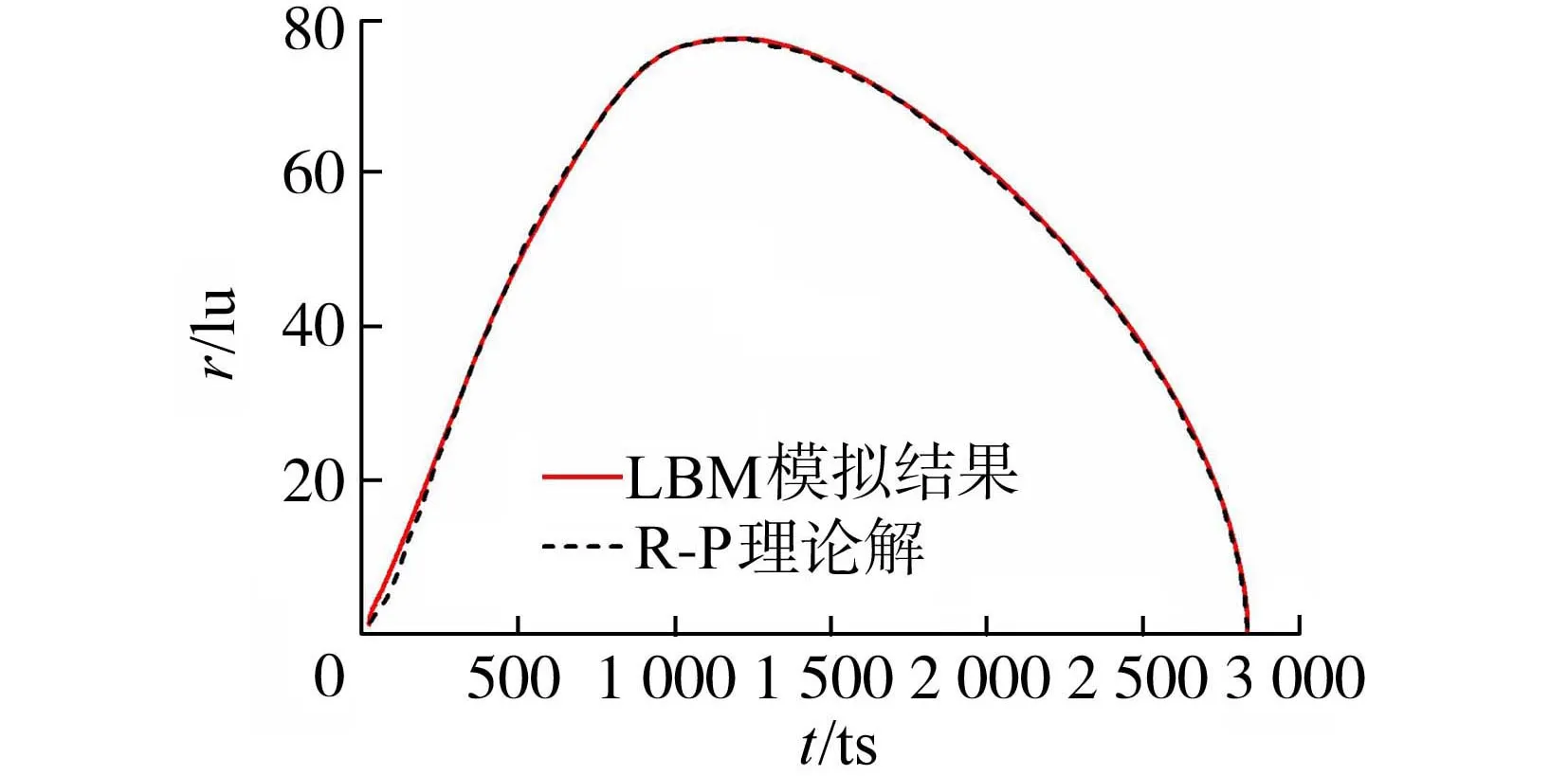
图2 LBM数值模拟结果与R-P理论解获得的空化泡半径演化过程对比

3 结果与讨论

为研究近壁区空化泡的初生和溃灭过程,选取500lu×500lu矩形计算域,温度初始化如式(15)所示,在气核激发点初始化一个半径为r0=5lu的高温区域。只有当初始激发温度高于流体当前压力下的临界温度时,才能实现液相转化为气相,形成气核。空化泡的生长通过边界及计算域内的流体低压实现,而溃灭则通过边界高压传递到计算域内实现。选取5种初始激发温度探究其对空化泡的影响,分别为1.0Tc、1.2Tc、1.4Tc、1.6Tc和1.8Tc。计算域边界为非平衡压力边界,底部边界为无滑移边界。计算域温度边界为非平衡外推常温边界,其顶部边界和左右两侧边界设置为T∞=0.5Tc,壁面温度同样设置为Tw=0.5Tc。空化泡内的初始压力和边界压力与第二节设置相同。

3.1 泡壁距离的影响

设置初始泡壁距离d=10～180lu,其对应的泡壁无量纲距离为γ=d/rmax=0.19～2.94。图3显示空化泡最大半径rmax随着无量纲泡壁距离的增大而增大。当γ<1.6时,空化泡生长过程中底部受壁面边界限制,当空化泡达到最大半径时无法保持圆形,空化泡最大半径与泡壁无量纲距离之间关系可表示为rmax∝γθ,在本研究中θ的取值范围为0.028～0.038。而当γ≥1.6时,空化泡生长始终保持圆形,空化泡最大半径rmax则与γ之间存在线性关系。图4为壁面最大流速uwmax、最大压力pwmax和最高无量纲温度Twmax/Tc随泡壁无量纲距离的变化。由于γ=0.19时空化泡在溃灭点即发生数值发散,因此无法捕捉到壁面最高温度,这里仅用空心点代替。由于泡壁无量纲距离增加,当γ<1时,空化泡溃灭后产生的微射流、压力波和高温将直接作用于壁面上,而随着泡壁无量纲距离的增加,壁面受到的冲击压力和冲击流速迅速减小。当γ≥2.2时,由于空化泡处于泡壁影响区外,壁面受到的冲击压力和最大流速逐渐趋于一致。

图3 泡壁无量纲距离和空化泡最大半径的关系

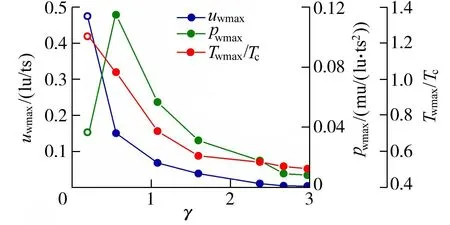
图4 Tini=1.2Tc时壁面最大流速、最大压力和最高无量纲温度随泡壁无量纲距离的变化

3.2 初始激发温度的影响

初始输入能量可以表示为

(16)

式中A为计算域面积。初始输入能量与空化泡最大半径之间的关系如图5所示,对于附壁型空化泡(0.18≤γ≤0.19)和近壁区游离型空化泡(1.55≤γ≤1.59,2.86≤γ≤2.92),与试验研究结论相同,空化泡最大半径与输入能量之间均为线性关系。这意味着可通过调节输入能量来获得可控大小的空化泡。图6展示了双对数坐标下无量纲输入温度Tini/Tc与空化泡最大半径rmax之间的关系,两者大致为幂函数关系,即rmax∝(Tini/Tc)θ,不同γ条件下的θ非常接近(对应图6的斜率),其值约为0.08。

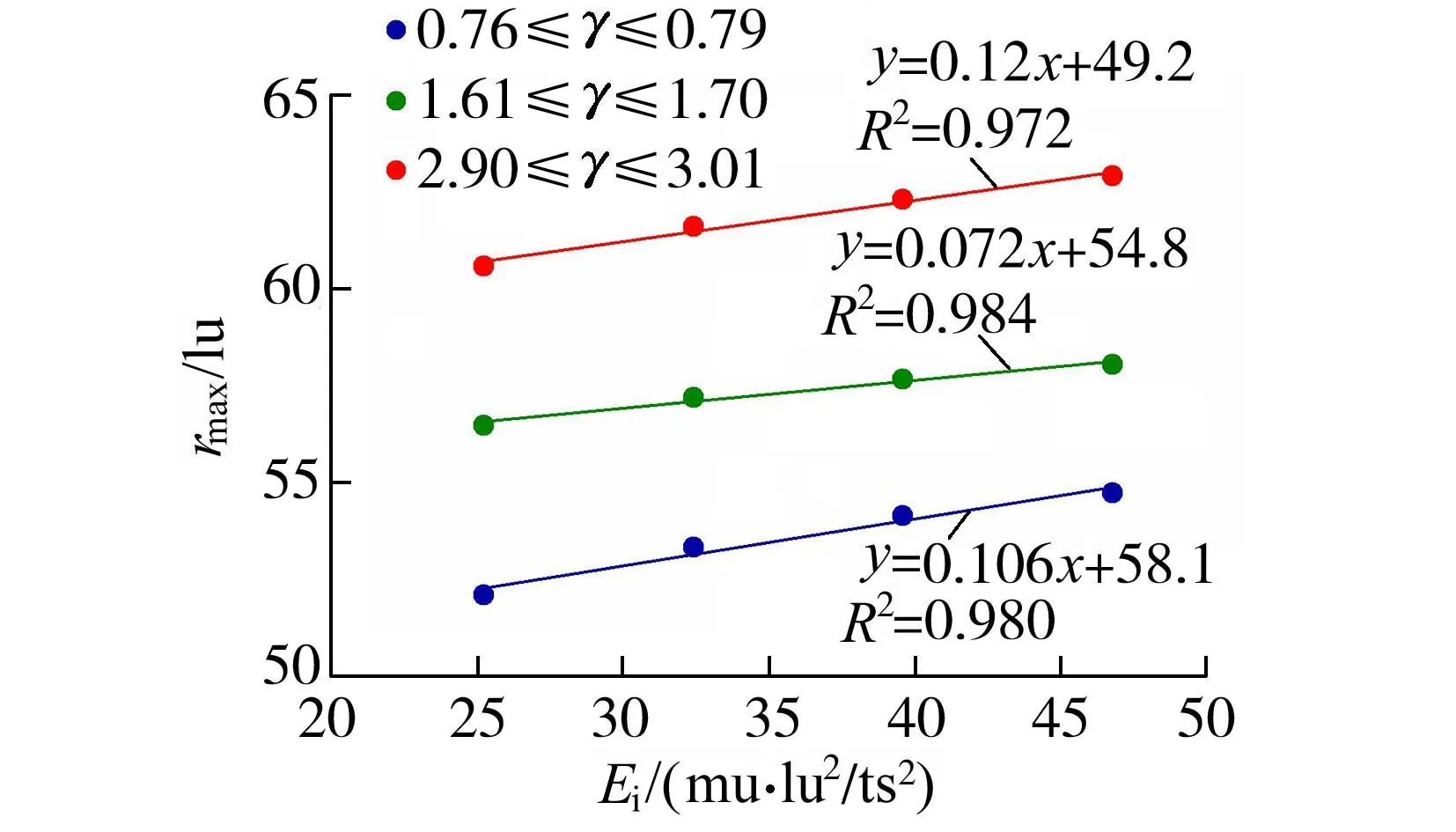
图5 初始输入能量与空化泡最大半径的关系

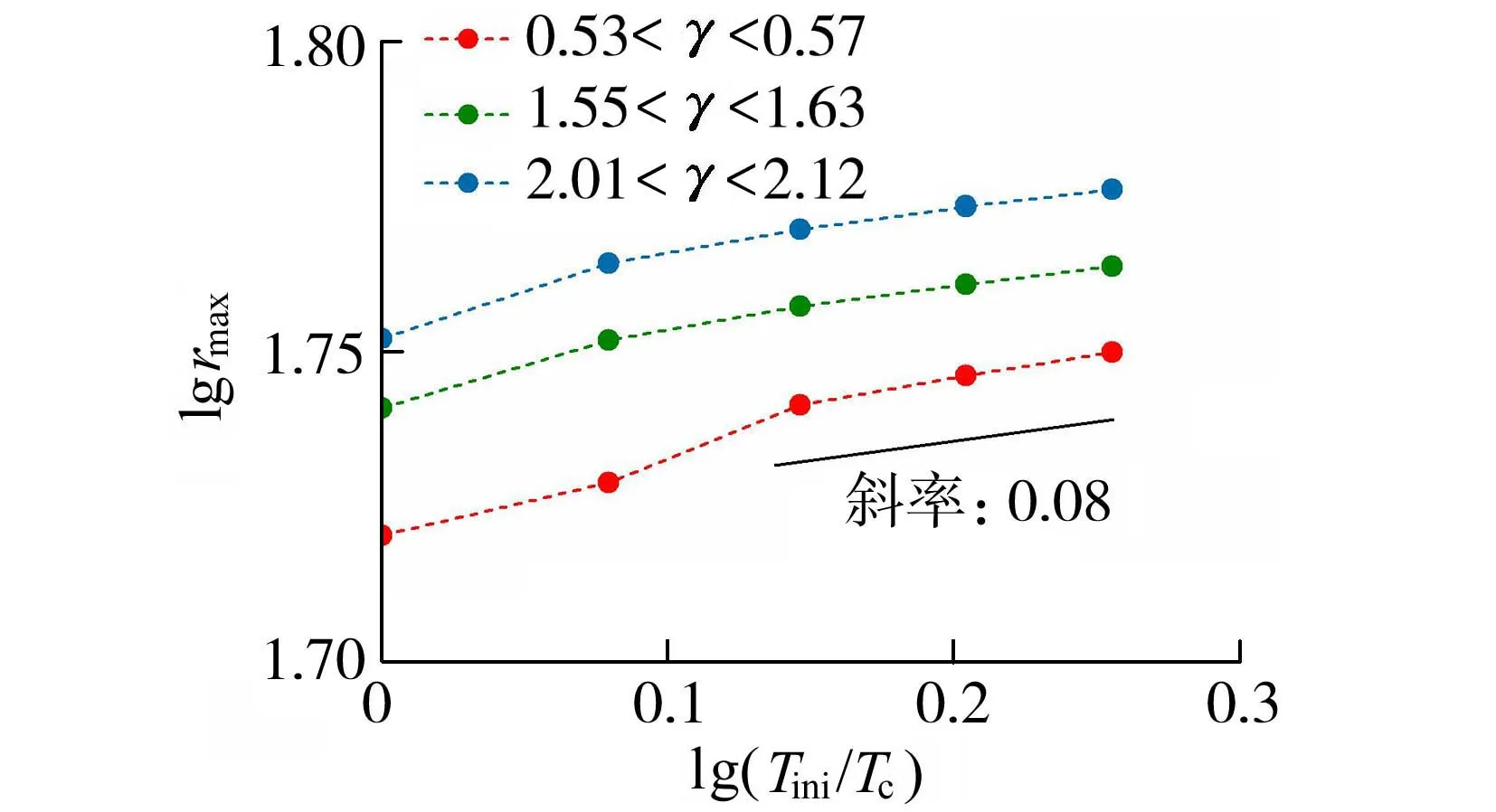
图6 空化泡最大半径与初始输入温度的关系

图7为d=90lu时不同初始激发温度条件下空化泡溃灭的形态变化,其中左侧为空化泡初生过程,右侧为空化泡溃灭过程。在空化泡溃灭的最终阶段,由于泡内温度随着初始激发温度的升高而增加,导致高温处的表面张力更小,空化泡抵抗非对称形变的能力变弱。最终导致空化泡在更大的半径时顶部即产生凹陷,形成更为集中的微射流。

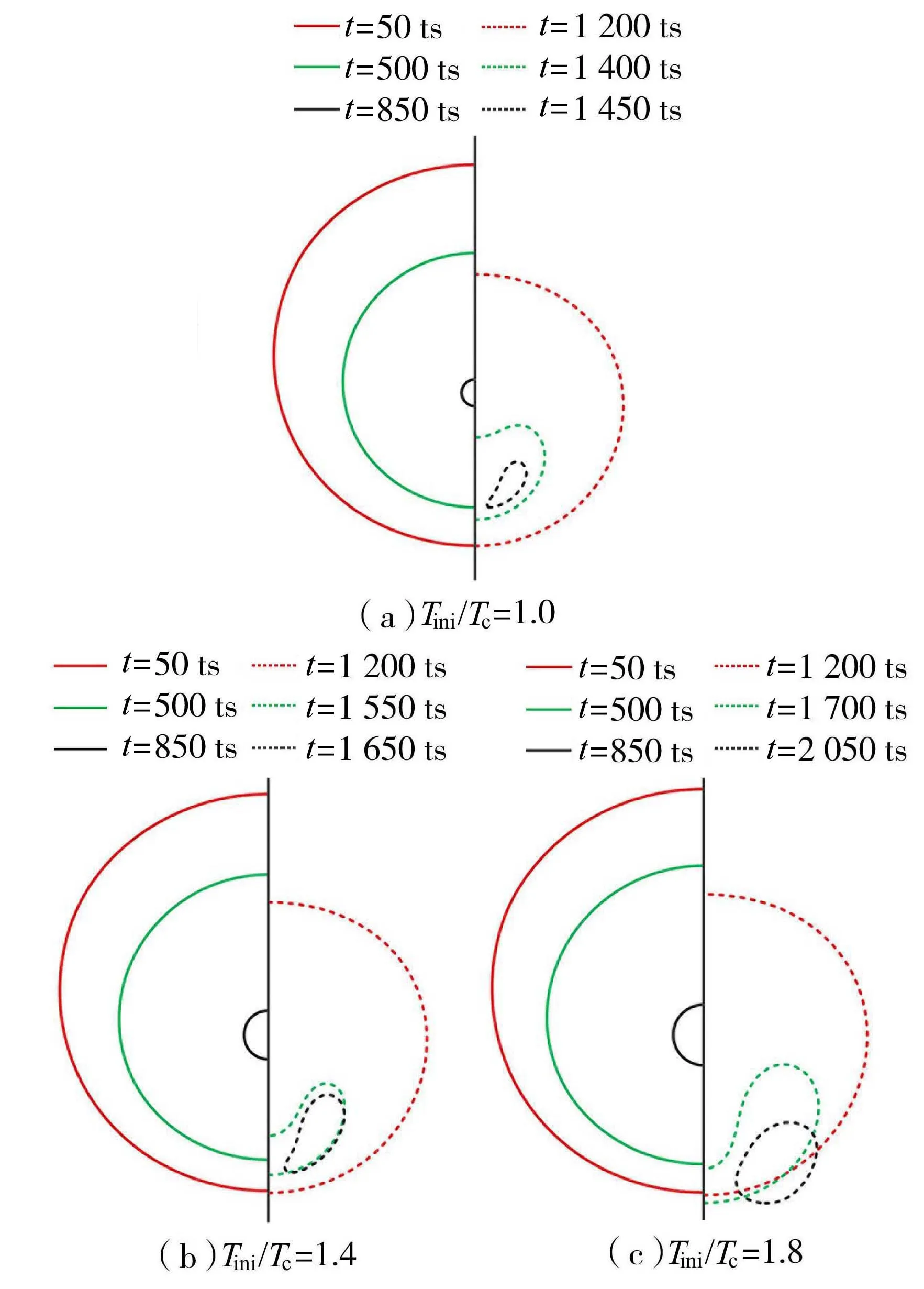
图7 d=90lu时不同初始激发温度条件下空化泡形态演化

空化泡演化数值模拟研究中,当流体工作温度远低于其临界温度时,通常将空化过程看作绝热过程,不考虑空化泡的热动力过程对水动力过程的影响,在这种情况下,可采用被动标量法对空化问题进行研究[15-17]。但对于工作温度处于临界温度附近的低温流体,其热动力过程尤为重要,空化泡演化过程中的温度变化往往导致界面上的表面张力处于持续变化的状态,因此有必要考虑热动力过程对水动力过程的影响。因此本文采用被动标量模型与热流耦合模型进一步对比了He等[10]的模拟结果,如图8所示,其中左侧为生长阶段,右侧为溃灭阶段。对于被动标量模型,在模拟中仅考虑流场对温度场的影响,而并不考虑温度场对流场的影响。对于被动标量模型,其计算压力场时式(5)中温度本文取为常温T=0.5Tc,因此其界面上的表面张力则保持常数σ=0.0102。模拟结果表明,当空化泡达到最大半径时,空化泡内与边界上的压力差极小,但对于热流耦合模型,在空化泡半径生长过程中,边界压力持续向计算域内做功,导致部分机械能转变为内能,空化泡周边环境温度高于0.5Tc,导致其表面张力较被动标量模型中更小。根据r=σ/Δp,表面张力越大,对应最大半径也越大,因此被动标量模型获得的最大半径更大。同时在溃灭过程中由于泡内气体发生相变转化为液体,并伴随着放热,其温度远高于0.5Tc,最终导致其射流体积更大,空化泡最终被击穿。

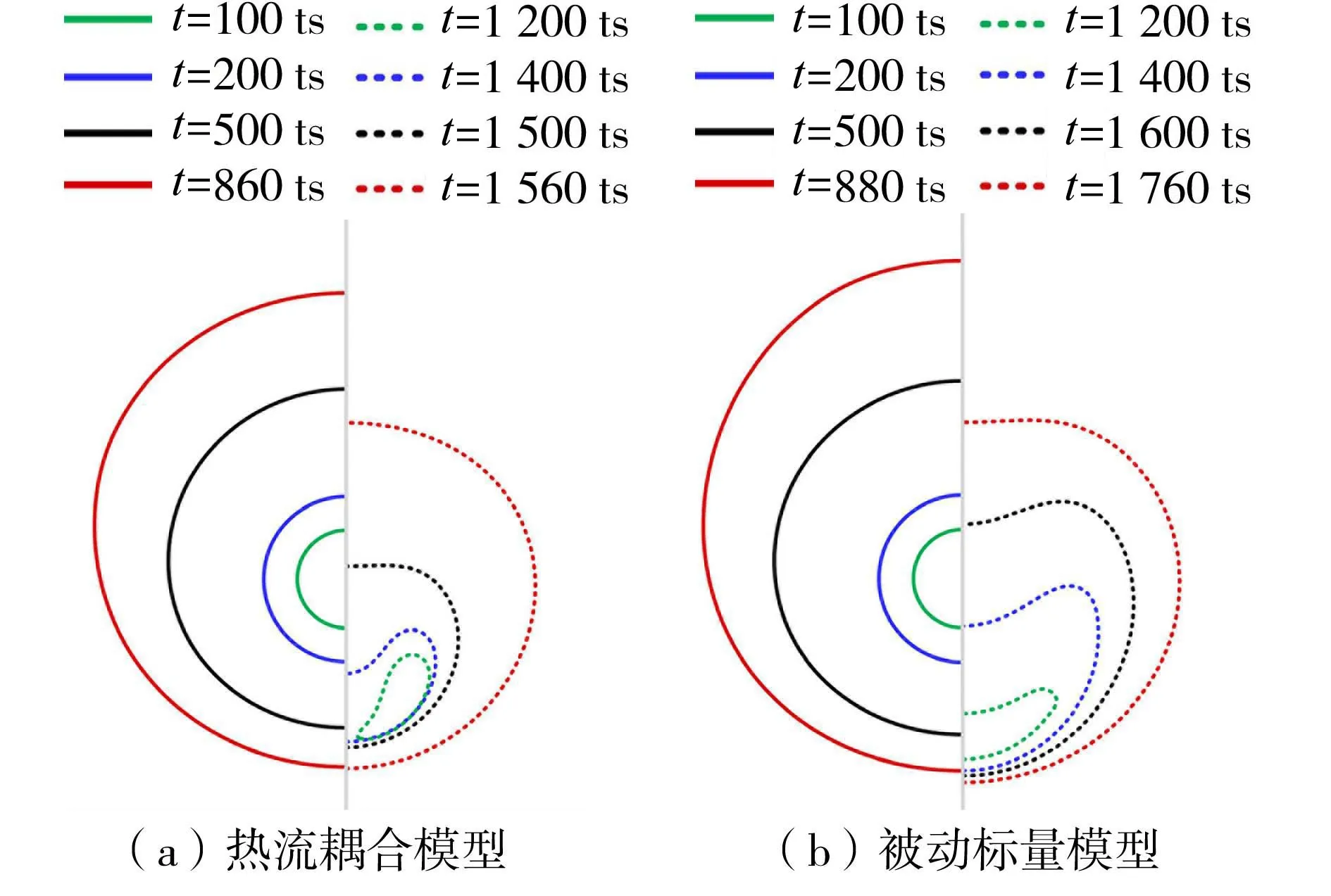
图8 不同模型获得的空化泡形态演化对比(d=90lu,Tini/Tc=1.4)

不同模型获得空化泡的溃灭时间、最大半径和空化强度的对比如表2所示。由于被动标量模型能获得更大的空化泡体积,且其表面张力更大,最终导致其溃灭时间比热流耦合模型获得的溃灭时间大9.8%。空化泡溃灭强度随着表面张力增大而增大[15],因此被动标量模型获得的空化泡溃灭时最大流速和最大压力比热流耦合模型分别大3.61%和6.52%,而溃灭温度则高9.3%。

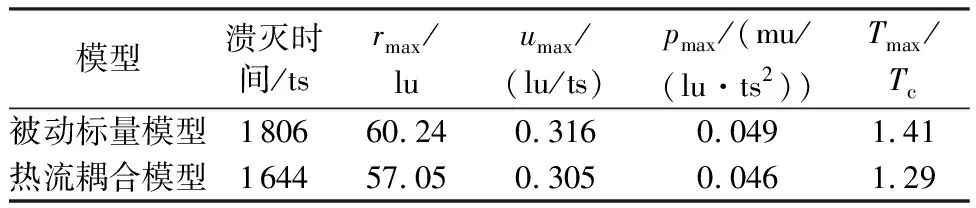
表2 不同模型计算获得的空化泡溃灭时间、最大半径和溃灭强度(d=90lu,Tini/Tc=1.4)

4 结 论

a.受壁面限制,当泡壁无量纲距离γ<1.6时,空化泡生长过程中无法保持圆形,其最大半径与泡壁无量纲距离之间为幂函数关系。当γ≥1.6,壁面影响减小,空化泡最大半径与γ之间为线性关系。

b.空化泡最大半径与输入能量之间为线性关系,与初始输入无量纲温度之间为幂函数关系,且θ值并不随泡壁无量纲距离的改变而改变。

c.热流耦合模型考虑了溃灭时高温对水气界面上表面张力带来的影响,与被动标量模型相比,在溃灭阶段获得的射流体积更大,微射流更集中,但溃灭强度小于被动标量模型。