基于卷积神经网络的高分六号卫星多光谱图像压缩

朱孟栩，张文豪，李国洪，顾行发，余 涛，4，郑逢杰，张丽丽，4，吴 俣，邴芳飞，唐健雄

（1.北华航天工业学院 遥感信息工程学院，河北 廊坊 065000；2.河北省航天遥感信息处理与应用协同创新中心，河北 廊坊 065000；3.中国科学院空天信息创新研究院 遥感卫星应用国家工程实验室，北京 100094；4.中科空间信息（廊坊）研究院，河北 廊坊 065001；5.航天工程大学 航天信息学院，北京 101416；6.天津大学 地球系统科学学院，天津 300072）

0 概述

随着传 感器技术的发展，星载多光谱图像的应用越来越广泛，多光谱图像包含更加丰富的光谱信息和空间信息。相对于单色图像，多光谱图像在农业、林业、国土、环保、气象、军事等领域有更大的应用价值。高分六号（Gaofen No.6，GF-6）卫星的多光谱图像在高分一号的基础上增加了红边波段，红边波段能够有效反映作物的光谱特性，在农业生产方面有着极高的应用价值［1］。GF-6 卫星的多光谱图像实现了高分辨率和宽覆盖的结合，空间分辨率达到16 m，幅宽达到800 km，具有8 个光谱波段，这使得图像包含了更丰富的观测信息。但是，由于其单景影像所占存储空间达到了10 GB 以上，对多光谱图像的传输和存储带来了极大困难，制约了多光谱图像的应用与发展。因此，高性能的多光谱图像压缩算法成为多光谱成像技术的重要研究方向。

传统的多光谱图像压缩算法主要包括基于预测的编码方法［2］、基于矢量量化的编码方法［3］和基于变换的多光谱图像压缩方法［4］这3 类：

1）基于预测的多光谱图像压缩方法是利用像素与波段之间的相关性，通过上下文信息预测当前像素值，实现多光谱图像的压缩。该类方法为无损压缩，能够无损地重建图像，但是图像的压缩率不够理想，并且压缩率会随图像的不同而出现较大的波动。

2）基于矢量量化的多光谱图像压缩方法是将多光谱图像的若干标量转化为一个矢量，将矢量空间整体化，从而达到压缩数据的目的。此类方法为有损压缩方法，其编码难度较高，压缩后会导致一部分信息丢失。

3）基于变换的多光谱图像压缩方法是将多光谱图像从空间域变换为频率域，在频率域范围内实现压缩编码。此类方法为有损压缩，压缩率可调，多光谱图像压缩率较大时会出现块效应，影响多光谱图像质量。

近年来，基于深度学习的图像压缩方法取得了比传统图像压缩方法更好的效果［5］。文献［6］开创性地将卷积神经网络应用在图像压缩领域，其利用自编码器对数据降维，生成特征矩阵，量化环节引入多进制量化，在反向传播时对量化图像添加随机误差，率-失真环节进行端到端的联合优化。随后，有学者对卷积神经网络图像压缩模型进行改进［7-10］，优化自编码器，改进量化结构，并提出了更加高效的熵编码模型，使得基于深度学习的图像压缩方法在精度和效率上都有一定的提升［11］。

当前，基于深度学习的图像压缩研究多数是基于普通照片，针对卫星影像特别是国产卫星影像的研究相对较少。随着我国卫星遥感技术的发展，国产卫星遥感影像在观测范围、波段数量、量化等级等方面均有显著提升，这使得卫星与地面之间、数据中心与用户之间的数据传输逐渐成为瓶颈。同时，卫星影像遥感应用对于观测数据十分敏感，因此，需要最大程度地保持原始信息不丢失，从而保证其定量遥感应用的效果。

针对上述问题，本文提出一种基于卷积神经网络的高分六号卫星多光谱图像压缩（Satellite Multispectral Image Compression，SMIC）模型。SMIC模型由自编码器、量化结构、熵编码3 个部分组成：自编码器提取图像特征，实现数据降维；量化结构将特征矩阵离散化，通过多进制量化减少量化环节的信息损失；熵编码去除空间冗余，降低码流。最后，通过实验比较不同压缩方法对多光谱图像的压缩率与重建质量，以验证SMIC 的多光谱图像压缩性能。此外，SMIC 为有损压缩，重建图像有一定的信息损失，为验证压缩后的多光谱图像是否能够满足定量遥感应用的需求，将同一地区、同一时间压缩前后的多光谱图像运用相同方法进行处理分析，从而验证本文所提多光谱图像压缩算法的可行性。

1 研究区域及数据

1.1 研究区域概况

以京津冀地区作为研究区域，京津冀地区位于华北平原，地理坐标为北纬36°01′～42°37′，东经113°04′～119°53′。京津冀地区地形复杂多样，由东南向西北逐级上升，平原、盆地、丘陵、山地、高原依次排列。京津冀地区地物类型丰富，包含林地、草地、裸地、水体、农作物等典型地物。

1.2 研究数据

本文研究数据为GF-6 卫星多光谱图像，多光谱图像是一种包含二维空间信息和一维光谱信息的三维数据立方体。GF-6 卫星16 m 多光谱宽幅相机共有8 个波段，观测幅宽为864.2 km，量化值为12 bit。GF-6 卫星具有观测范围大、重返周期短、定量化探测的优势，能提供高时空分辨率的多源数据。本文研究数据采用的是2020 年京津冀地区不同季节的GF-6卫星L1A 级产品。

研究数据分为实验数据和测试数据。实验数据包含不同地物、季节和天气的多光谱图像，图像尺寸为256×256像素，共 有23 000 张。测试数据为6 张1 024×1 024像素的多光谱图像。数据预处理流程如图1所示。

图1 数据预处理流程Fig.1 Data preprocessing procedure

首先将获取的研究数据进行裁剪，裁剪成256×256 像素和1 024×1 024 像素的多光谱图像；然后将TIF 格式图像转为矩阵，并进行最大值最小值归一化处理，处理后的矩阵转成张量输入到SMIC模型。

研究数据的量化值为12 bit，取值范围为［0，4 095］，采用最大值最小值归一化的方法将数据的取值范围量化到［0，1］。归一化后的数据输入到SMIC 模型。最大值最小值归一化如式（1）所示：

其中：Xq为量化后的数值；X为量化前的数值；Xmax和Xmin分别代表研究数据的最大值和最小值。

2 研究方法

2.1 SMIC 模型

针对GF-6 卫星多光谱图像波段数量多、数据量大的特点，本文结合深度学习图像压缩模型，提出SMIC 模型，用于压缩GF-6 卫星多光谱图像。SMIC模型的整体技术路线如图2 所示，3 个模块的具体功能如下：

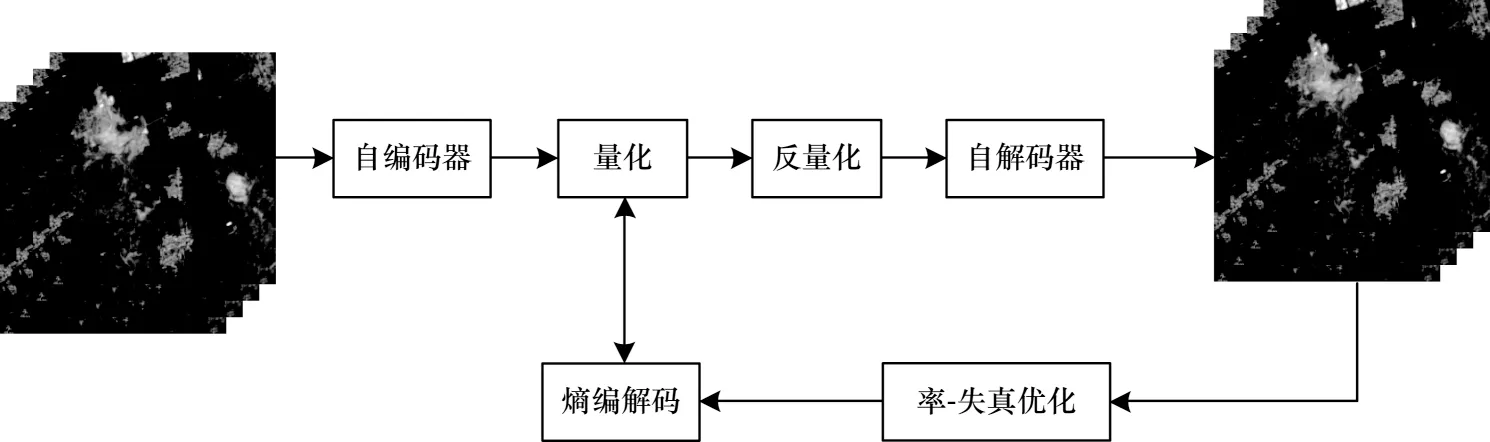
图2 SMIC 模型整体技术路线Fig.2 Overall technique flowchart of SMIC model

1）自编码器通过卷积下采样和重建归一化层提取多光谱图像特征，并降低多光谱图像数据的尺寸，实现多光谱图像数据降维，达到初步压缩数据的目的。

2）量化结构采用多制量化到整系数，将自编码器初步压缩后的多光谱图像数据进一步压缩。

3）熵编码采用高斯混合模型对量化之后的数据进行处理，输出码流，采用算术编码，去除多光谱图像的空间冗余。

在多光谱图像重建环节，码流经过熵解码模型还原数据，还原后的特征图像通过反量化、自解码器还原成重建图像。率-失真优化对多光谱重建图像的失真和码率联合调优，不断优化网络参数，得到更好的多光谱重建图像。SMIC 模型由自编解码器、量化结构、熵编码、率-失真优化等环节构成，模型具体结构如图3 所示，其中：Q 代表量化；AE 代表算术编码；AD 代表算术解码；IQ 代表反量化。

图3 SMIC 模型结构Fig.3 Structure of SMIC model

2.1.1 自编码器

自编解码器［12-14］包含自编码器和自解码器2 个部分。自编码器由编码器和超参编码器2 个部分组成，用于提取多光谱图像的特征信息，降低多光谱图像的维度。自编码器主要有卷积层、重建归一化层［15-16］、LeakyReLU 激活函数［17］组成。自解码器由解码器和超参解码器2 个部分组成，用于重建编码后的图像，自解码器采用和自编码器完全对称的结构。

编码器包含卷积层和重建归一化层，在保留图像主要信息的同时降低了图像的数据量，将多光谱图像的尺寸降为原图的1/16，并将输入的8 通道多光谱图像输出为320 通道的特征图。卷积层采用步长为2 的5×5 卷积核，对多光谱图像进行下采样。重建归一化层将卷积下采样得到的特征图进行归一化处理，其作用和卷积神经网络中的BN 层相同，能够很好地联合处理非线性特征，并可以捕捉多光谱图像的统计特性。相比于BN 层，重建归一化层的优点在于其没有添加噪声，更加适合多光谱图像重建，重建图像更清晰，有利于多光谱图像压缩。重建归一化层如式（2）所示：

其中：xi代表第i层输入的特征图；βi和γi代表需要学习的参数；yi代表第i层输出的特征图。

超参编码器能够进一步降低数据维度，提取图像的深层特征信息。超参编码器采用2 种卷积核进一步降低数据维度，即步长为1 的3×3 卷积核和步长为2 的5×5 卷积核，超参编码器的卷积下采样操作将图像尺寸降为原图的1/64。超参编码器部分采用LeakyReLU 激活函 数，LeakyReLU 继承了ReLU 收敛速度快的优点，同时保留了一些负数数值，特征图像的负数信息不会全部丢失。LeakyReLU 激活函数可以由式（3）表示：

其中：ai是(1,∞)区间内的固定参数。

自解码器采用和自编码器完全对称的结构，自解码器利用卷积层、反重建归一化层重建多光谱图像。卷积层对自编码器的特征图进行上采样，还原成多光谱图像原有的尺寸。反重建归一化层连接2 个卷积层。反重建归一化层如式（4）所示：

其中：表示第i层输入 的特征 图；表示第i层输出的特征图。

2.1.2 量化结构

为了实现编码压缩的目的，经过自编码器提取得到的多光谱图像特征图需要进行量化处理。量化过程会给多光谱图像压缩带来信息损失，高效的量化结构是提高影像多光谱重建图像质量的关键。本文方法量化结构采用的是多进制量化到整系数［18］，此方法能够减少量化环节的信息损失，并使端到端的训练更加高效。考虑到量化过程不可微，量化结构通过添加均匀噪声来模拟量化过程，以保证梯度反转，实现量化过程可微。

2.1.3 熵编码

多光谱图像经过自编码器提取特征和量化之后，还存在冗余去除不彻底的情况，需要依赖高效的熵编码环节去除多光谱图像冗余，进一步提高编码性能。

熵编码通常采用单高斯模型，单高斯模型具有较好的编码性能。针对GF-6 卫星多光谱图像波段多、数据量大的特点，本文使用高斯混合模型［19］，高斯混合模型提升了编码性能，进一步提高了图像压缩效率。高斯混合模型的分布函数如式（5）所示：

其中：ωi代表不同高斯模型的权重；F代表不同的高斯模型；N(ui,σi) 代表模型的高斯分布参数；代表熵编码结果。本文采用双高斯混合模型，2 个高斯模型的权重分别为ωi和1-ωi。

2.1.4 率-失真优化

对于端到端的编码，率-失真优化是对图像失真和压缩码率的联合调优，码率估计和图像失真将直接影响整个结构的优化效果。为了更好地优化多光谱图像的压缩性能，需要在图像的码率与失真之间进行权衡。SMIC 模型的率-失真优化［20］采用的损失函数如式（6）～式（8）所示：

其中：D表示失真，原始图像与重建图像的均方误差代表图像的失真程度；R表示码率；λ表示失真与码率的平衡系数；代表失真度；分别代表与的码率；分别代表与的分布。SMIC 模型在训练过程中调节图像损失和码率的分配，使得图像损失和码率之间达到均衡，同时保证多光谱图像的重建质量和压缩效率。

2.2 图像压缩性能参数

有损图像压缩的性能评价主要有2 个方面：第1 个是用来衡量图像压缩前后数据量的变化情况，常用的评价指标为压缩比（BPP）；第2 个是用来衡量图像压缩重建之后的信息损失情况，常用的评价指标为图像的峰值信噪比（PSNR）。

压缩比［21］用来计算图像的压缩效率，是未压缩图像大小与压缩图像大小的比值，计算如式（9）所示：

其中：B1和B2分别代表压缩前后图像占用的存储空间。

峰值信噪比PSNR 利用压缩前后2 张图像的均方误差(MSE)来衡量图像压缩重建之后信息的损失程度，计算如下：

其中：K代表图像的通道数；M∙N代表图像的大小；I(i,j)代表压缩前(i,j)位置的像素值；J(i,j)代表压缩后(i,j)位置的像素值。重建图像的PSNR 值越大，代表重建图像与原始图像之间的信息损失越少。

2.3 卷积神经网络参数设置

在本文实验中，SMIC 模型训练是在内存为8 GB 的NVDIA GeForce GTX 1080 的GPU 下进行的。因为GF-6 卫星多光谱图像有8 个波段，为了防止训练过程中内存溢出，在SMIC 模型网络参数设置中，卷积神经网络一次只处理一张图像，网络参数batch_size 设置为1。在率-失真损失阶段，通过设置不同的λ值，控制图像压缩的码率，实现不同码率的压缩。本文实验中λ的值设置为256、1 024、2 048、4 096、8 192 和16 384，不同的λ值控制SMIC 模型的码率。网络训练优化使用Adam 优化器，总的迭代次数为2 500 000 次。在SMIC 模型训练初始阶段，为了加快拟合速率，初始学习率设置为0.000 1，当训练迭代次数到250 000 次时，SMIC 模型的损失函数值出现振荡，调整学习率为0.000 01，从而提升拟合程度，提高图像的压缩质量，达到更好的压缩效果。

3 实验验证

3.1 模型性能评价

在本文实验中，通过计算训练过程中各个训练世代（Epoch）的损失函数值来评价SMIC 的性能［22］，图像的损失函数值是通过原始图像和重建图像的均方误差和压缩后的码率计算而来。图4 展示了多光谱图像信息损失与Epoch 的关系，模型在训练到Epoch 为6 时，重建图像的信息损失值趋于稳定，并且此时图像的信息损失值达到较低的水平。综合模型训练次数和损失函数值可以得出，Epoch 为6 时保存的SMIC 模型参数为最佳选择。

图4 模型训练信息损失曲线Fig.4 Loss curve of model training information

3.2 实验结果分析

多光谱图像既包含二维空间信息也包含一维光谱信息，为了验证SMIC 的性能，从多光谱图像峰值信噪比PSNR 的角度将SMIC 与JPEG 算法的压缩性能进行比较，计算2 种多光谱图像压缩算法在不同码率下的PSNR 值，结合实验测试数据的6 张多光谱图像得到图像的平均PSNR 值。2 种压缩算法的平均PSNR 值计算结果如图5 所示。

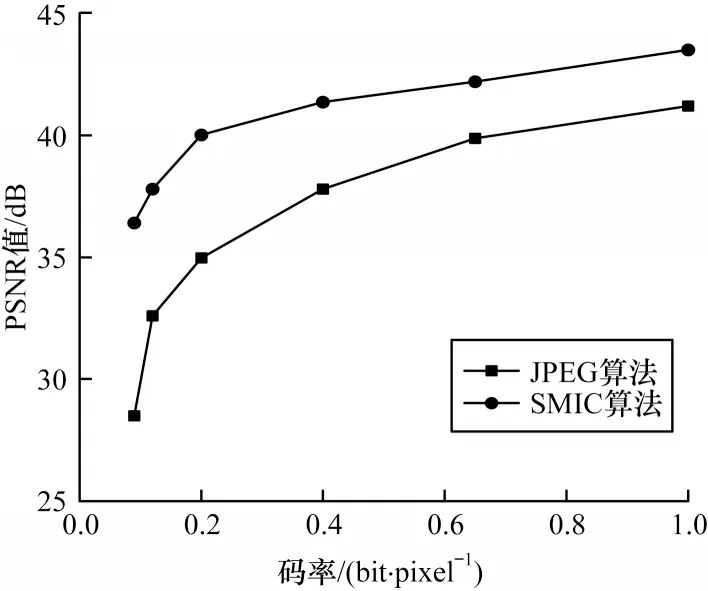
图5 不同码率下的测试数据PSNR 值Fig.5 PSNR values of test data under different code rates

为了更加直观地比较不同压缩算法对GF-6 卫星多光谱图像的重建效果，选取测试数据中的6 张多光谱图像，利用SMIC 与JPEG 压缩算法［23］分别对多光谱图像进行压缩和重建。为更清晰地展示重建图像，通过ENVI软件对多光谱图像进行RGB 波段合成，结果如图6 所示。

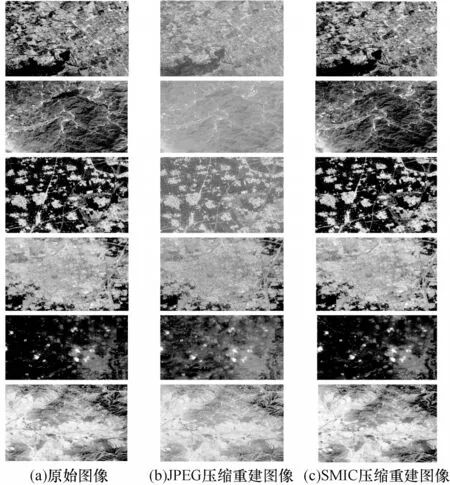
图6 重建图像比较Fig.6 Reconstruction images comparison

通过比较不同压缩算法的重建图像可以看出，JPEG 压缩算法重建图像具有明显的块效应，在不同类型地物的边界存在部分像素点有较大误差的问题，并且误差较大的像素点集中出现在不同地物的过渡地带，如村镇-农田、城镇-林地等。JPEG 压缩重建图像的色度相较于原始图像存在明显的失真情况，城镇、道路等人工目标尤其明显。SMIC 压缩重建的图像在视觉上更接近原始图像，无明显的亮度和色度差异，能够较好地还原出不同地物。

对重建图像进行定量分析，随机选取1 个点，分别读取原始图像、JPEG 压缩算法重建图像、SMIC压缩算法重建图像的8 波段像素值，结果如图7（a）所示。随机选取原始图像红边波段中连续的70 个点，分别读取JPEG 压缩算法重建图像、SMIC 压缩算法重建图像相应位置的像数值，结果如图7（b）所示。

图7 不同压缩算法重建图像的DN 值对比Fig.7 Comparison of DN values of reconstructed images using different compression algorithms

为了更加清楚直观地显示重建图像的误差分布，统计2 种图像压缩算法重建图像的误差，误差统计直方图如图 8 所示。由图8 可得，本文算法的误差值主要集中在［-100，100］范围内，区间占比达到80%以上，JPEG 压缩算法的误差值在［-100，100］范围内的占比接近50%，由此可得，较JPEG 压缩算法，SMIC 压缩算法重建的图像更接近原始图像。

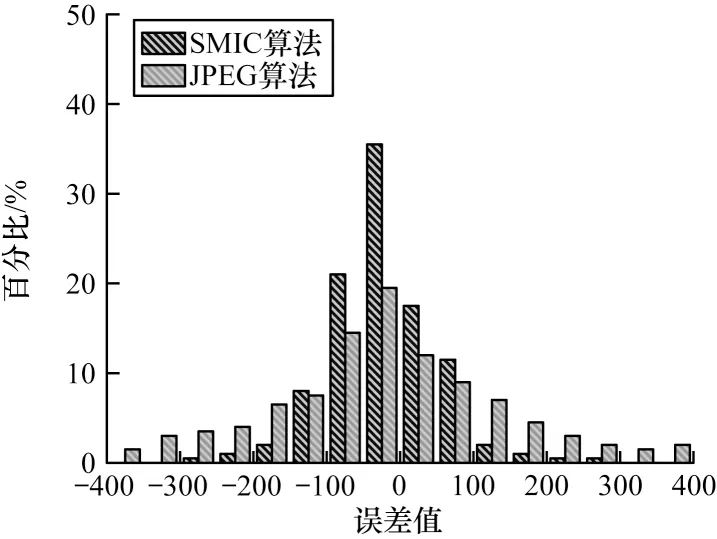
图8 不同压缩算法重建图像的误差统计直方图Fig.8 Error statistical histograms of reconstructed images using different compression algorithms

3.3 定量遥感应用实验

GF-6 卫星除了常规的红、绿、蓝、近红外段外还增加了中心波长为710 nm 和750 nm 的红边波段，红边波段能够有效反映农作物的叶绿素含量和特有的光谱属性。红边光谱的变化可提供比红绿波段和短波红外更丰富的红边区域波谱信息［24］。本文分别构建归一化植被指数NDVI 和红边归一化植被指数NDVI710，以验证重建图像质量。NDVI 和NDVI710的计算公式分别如式（12）、式（13）所示：

其中：B3、B4、B5分别对应GF-6卫星多光谱图像红波段、近红外波段和中心波长为710 nm 的红边波段。

对不同压缩算法的重建图像分别计算NDVI、NDVI710，利用NDVI 值对冬小麦进行反演，参考文献［25］，本文实验将NDVI 值在［0.54，0.68］区间的地物判别为冬小麦，实验结果如图9 所示（彩色效果见《计算机工程》官网HTML 版）。由图9 可得，SMIC 压缩算法的冬小麦反演结果和原图较为一致，JPEG 压缩算法的反演结果有明显异常点，存在将村庄中地物识别为冬小麦以及冬小麦地块中部分点反演成其他地物的问题。原始图像共有466 628 个像素点反演为冬小麦，对2 种压缩算法的反演结果进行定量分析可知：SMIC 压缩算法共有425 749 个像素点判别为冬小麦，和原始图像反演结果对比，有406 720 个相同的像素点，准确率为87.16%，冬小麦误检率为4.47%；JPEG 压缩算法共有475 429 个像素点判别为冬小麦，和原始图像反演结果对比，有403 460 个相同的像素点，准确率为86.46%，冬小麦误检率为15.13%。

图9 归一化植被指数和冬小麦反演结果Fig.9 Normalized vegetation indexes and inversion results of winter wheat

对NDVI 进行分析，统计原始图像、JPEG 压缩算法重建图像、SMIC 压缩算法重建图像的NDVI 取值情况，分别绘制SMIC 压缩算法重建图像NDVI 与原始图像NDVI 的散点图、JPEG 压缩算法重建图像NDVI 与原始图像NDVI 的散点图，结果如图10 所示，计算得到：SMIC 压缩算法重建图像NDVI 与原始图像NDVI 的决定系数R2为0.93，拟合方程的斜率为0.94；JPEG 压缩算法重建图像NDVI 与原始图像NDVI 的决定系数R2为0.72，拟合方程的斜率为1.16。由此可得，SMIC 压缩算法的重建图像比JPEG 压缩算法的重建图像更接近原始图像。

图10 NDVI 散点图对比Fig.10 NDVI scatter diagram comparison

4 结束语

本文提出一种基于卷积神经网络的GF-6 卫星多光谱图像压缩模型SMIC，该模型通过自编码器、量化环节、熵编码对多光谱图像进行压缩，利用率-失真优化平衡多光谱图像的失真和码率，提升多光谱图像的压缩性能。实验结果表明：在高码率下SMIC 压缩重建图像的PSNR 值达到45 dB，较JPEG压缩重建图像的PSNR 值高2 dB，SMIC 压缩重建图像在视觉上更接近原始图像；SMIC 压缩重建图像的像素误差值主要集中在［-100，100］范围内，区间占比达到80%；SMIC 压缩重建图像的冬小麦反演结果总体上与原图一致，重建图像NDVI 与原始图像NDVI 的决定系数R2为0.93，其冬小麦反演精度与JPEG 压缩算法反演精度相当，均为85% 左右，但SMIC 的误检率比JPEG 压缩算法低10%。本文所提SMIC 压缩模型能够较好地还原GF-6 卫星多光谱图像的光谱特征和空间特征，在一定程度上能够满足部分定量遥感的应用需求。下一步将探讨包含更多光谱信息的国产高光谱卫星遥感图像压缩问题，拓展SMIC 压缩模型的应用范围。