图数据精确最短距离的隐私保护外包计算方案
于莹莹,丁红发,2,蒋合领,3
(1.贵州财经大学 信息学院,贵阳 550025;2.贵州省大数据统计分析重点实验室,贵阳 550025;3.贵安新区科创产业发展有限公司,贵阳 550025)
0 概述
随着在线社交网络、出行导航、通信网络、生物蛋白分析等图数据应用与服务的蓬勃发展,海量图数据的收集、管理和分析技术受到业界的广泛关注。海量图数据的广泛应用和大规模分析所需的资源已超出数据所有者提供资源的能力,加之云计算的日益普及,数据外包成为数据应用的主流方式。使用云服务对图数据进行存储和计算,能显著降低本地的存储和管理成本。例如,东部发达地区的图数据服务企业将数据存储和计算迁移至西部低成本的云计算中心。然而,海量图数据中包含大量个人隐私(如身份信息、位置信息等)[1-2]、商业秘密等敏感信息,外包过程中数据所有者失去了对数据的实际控制,个人隐私和商业秘密极易受到损害。例如,Facebook 用户社交网络、滴滴道路网络等隐私泄露事件。因此,隐私敏感的数据在外包前,特别是在云服务提供商不可信的情况下,应该在本地进行加密。然而,传统加密工具阻碍了数据的利用和计算,直接破坏了数据的可用性[3]。如何在数据外包等非受控环境下进行数据保护和高效计算已成为学术界和产业界关注的热点问题。
为了解决上述问题,学术界不断探索新的解决方案,如k-匿名[4]、差分隐私[5]、加密算法[6-7]、安全多方计算[8-9]等图数据隐私保护方法。现有的各类图数据隐私保护方法中,基于密码算法与协议的方法能够严格保护图数据信息且不改变图数据的原有结构特征,故该类方法在面向图数据结构特征计算的外包服务场景中[10-11]备受关注。
最短距离查询作为图数据最基本的结构查询[12-13],在社交网络的用户间最短社交次数分析、生物网络蛋白质功能的相关性分析、通信网络中最短呼叫次数分析等众多查询服务中均有广泛的应用。由于对图数据安全的紧迫需求,基于加密图数据的最短距离查询外包计算在实际应用中有广泛的需求,其主要过程为:图数据所有者在本地加密其持有的原始图数据集,并将加密后的图数据外包给云服务提供商;云服务提供商向图数据查询请求者(数据所有者或查询请求用户)提供基于密文图数据的最短距离查询外包服务;查询请求者对查询请求加密后提交给云服务提供商;云服务提供商对密文查询请求进行计算处理,并返回密文计算结果;查询请求者对收到的密文查询结果解密,得到明文结果。该方法一方面凭借云服务提供商强大的存储和计算能力解决数据拥有者的本地计算资源问题;另一方面利用加密的方法对原始图数据和查询请求进行保护,保证图数据的节点隐私、边隐私和用户查询请求隐私。
然而,在大规模密文图数据上计算最短距离消耗资源巨大,且在查询计算过程中会因图数据信息的存储不当造成在计算时隐私信息泄露;此外,云服务提供商往往并非完全诚实,甚至是恶意的,其会旁路观测或攻击计算过程以获取真实图数据。因此,设计高效的图数据最短距离安全外包计算方案,并进一步减少信息泄露是当前亟待解决的问题。
现有的密文图数据最短距离安全外包计算可分为两类。第1 类聚焦加密图上的模糊最短距离查询,常采用距离预言的方法对预言距离值进行加密,以有效计算任意两个顶点之间的近似距离。该类方法以牺牲计算精度为代价提高查询效率,在距离预言的预计算阶段资源消耗过大且图数据的相关隐私信息存在泄露的风险。第2 类聚焦密文图数据的精确最短距离计算,通过对原始图数据进行实例化加密,并在此基础上进行精确计算,能够通过减少存储过程中的信息泄露问题保护图数据隐私。该方法在复杂密文图数据上计算高准确性的结果,其计算时间复杂度高,导致效率降低。因此,如何在密文图数据上设计高效、安全的精确最短距离查询计算方案成为当前的重要挑战之一。
针对密文图数据的最短距离查询存在效率低、安全性差的问题,本文基于二跳覆盖标记提出加密图数据精确最短距离外包计算方案,以实现隐私保护的最短距离查询,并在减少图数据隐私泄露的同时提高计算和存储效率。首先,基于二跳覆盖标记对原始图数据生成原始标记集合,再通过广度优先搜索修剪策略对原始标记集合进行修剪,获得修剪后的标记集合。然后,利用伪随机函数对标记中的邻接节点构造虚假的节点信息,结合加法同态对标记中的距离值进行加密,保证加密图数据的节点隐私和边隐私。最后,基于节点令牌和加密标记构造安全索引结构,并根据查询请求递归计算索引中对应的距离候选结果集合,实现高效的密文图数据外包最短距离查询计算。
1 相关工作
图数据作为一种能够刻画事物普遍联系的数据结构,在被众多挖掘分析应用需求的同时,其隐私和安全外包计算也受到广泛关注。CHASE 等[14]把可搜索加密技术引入图数据,首次提出图加密的概念以保护图数据的隐私和查询请求,并实现了密文图数据上的邻接查询和标记图上的集中子图查询。CAO 等[15]通过预先构建基于特征的索引来提供加密图数据的特征相关信息,解决了云计算中加密图数据的关键字查询与相交子图查询问题。与此同时,安全多方计算也被用于解决隐私保护的图数据查询问题,然而其并不适用于大规模图数据。
为在大规模密文图数据上实现高效的计算查询,YIN 等[16]探索了图数据的隐私保护可达查询外包计算问题,基于隐私保护的二跳标记设计了图数据的可达性查询方案,并提出近似最短距离查询方案。MENG 等[17]通过计 算距离 预言机(distance oracle),并利用部分同态加密构造图数据同态加密方案,在加密的距离预言上实现近似最短路径查询,但该方案在距离值相差较大时会牺牲准确率,造成较大误差。ZHU 等[18]提出一种基于加密图数据的支持同义词查询的最短路径搜索方案,通过词干算法和加密机制将节点转化为令牌并建立安全索引,查询索引中节点的同义词进行最短路径搜索。沈蒙等[19]提出一种基于图压缩的支持近似最短距离查询的图数据加密机制,提高了图数据计算的查询效率。LIU等[20]提出基于二跳覆盖标记索引的图数据加密框架,构造一种保序加密方案以执行近似最短距离查询,并精确定义图数据加密方案的隐私泄露程度。为在加密图数据上实现带约束的最短距离查询,SHEN 等[21]基于部分同态加密和保序加密提出一种高效的近似约束查询的图加密方案,但该方案泄露了路径开销的顺序信息。加密图数据的近似最短距离查询虽然效率高,却牺牲了最短距离结果的精度。在无线通信、物联网等场景中往往需要查询精确的最短距离,因此,密文图数据上的精确最短距离计算亦十分重要。为实现密文图数据上的精确最短距离查询,WANG 等[22]提出基于加法同态的安全图数据加密方案,该方案支持加密图数据上边动态更新的精确最短路径查询外包计算。GHOSH 等[23]提出支持递归的结构化加密方案,能够有效查询密文图数据单源最短路径,采用SP 矩阵优化数据结构以提高查询速度。DU 等[24]提出一种结构化的图数据加密方案并扩展至密文图数据查询系统,支持精确最短距离等多类基础性图数据查询服务。为进一步提升精确最短距离查询的灵活性,ZHANG 等[25]提出支持带约束的精确最短距离查询的隐私保护图数据加密方案,利用安全整数比较协议及安全最小值协议保护图数据隐私,但该方案的计算效率较低。相比近似最短距离查询,带约束的最短距离查询[26-27]是一种既考虑最短距离又考虑成本条件的特殊查询。最短距离查询的外包隐私计算吸引了众多学者深入研究[28-29]。
综上可知,密文图数据上最短距离外包计算方案难以同时提升结果准确性、计算效率和安全性。在密文图数据的最短距离查询过程中,如何在降低计算时间和空间开销的同时提高计算结果的准确性,仍是一个难题。针对该问题,本文设计密文图数据上安全、高效的精确最短距离查询外包计算方案。该方案基于二跳覆盖标记生成图数据的原始标记集合,并通过广度优先搜索修剪策略对原始标记集合进行修剪,减少预计算的标记,减小索引结构的尺寸。同时,在所构造的同态加密索引结构基础上,利用安全索引计算精确最短距离并提高图计算的检索效率。
2 基本定义
本节介绍图数据最短路径计算相关的符号定义,并介绍所涉及的基础知识。
2.1 符号定义
G=(V,E)是一个具有顶点集V和边集E的图,G的顶点总数可表示为|V|,边的总数表示为|E|。图G的顶点集和边集分别由V(G)和E(G)表示,顶点v∊V的邻居节点表示为NG(v),即NG(v)={u∊V|(u,v)∊E};v的标记信息存储其邻接顶点及边长,由L(v)表示。设dG(u,v)表示顶点u和v之间的距离,若u和v在G中不相连,则定义dG(u,v)=∞。给定最短距离查询请求q=(s,t),查询顶点s到顶点t之间的最短距离ds,t,密文最短距离用Ds,t表示。概率算法A 的输出x用x←A 表示,确定性算法ℬ 的输出x用x:=ℬ 来表示。在整个过程中,所有算法都隐式地将安全参数λ(λ∊N)作为输入。
为了便于阅读,表1 列出了本文方案涉及的符号及其描述。

表1 符号及其描述 Table 1 Symbols and their descriptions
2.2 相关知识
本节主要介绍二跳覆盖标记、伪随机函数、伪随机排列、字典等相关知识。
1)二跳覆盖标记。对于图G中的任意顶点v,选取一个候选顶点集合S(v),S(v)存储顶点v的邻接节点。任意顶点对(s,t)之间的最短路径上至少有一个顶点u满足u∊S(s),u∊S(t)。对于每个顶点s和一个顶点u∊S(s),预先计算两者间的距离dG(s,u),称集合L(s)={(u,dG(s,u))u∊S(s)}是顶点s的标记,L(s)的长度为L(s)中(u,dG(s,u))对的个数。所有顶点的标记集合{L(v)}v∊G即为二跳覆盖标记。利用标记可以清楚计算出两个顶点s和t之间的距离dG(s,t),并通过“min”计算出最短距离。图1 所示为二跳覆盖标记下获得顶点s和t之间的最短距离示例。
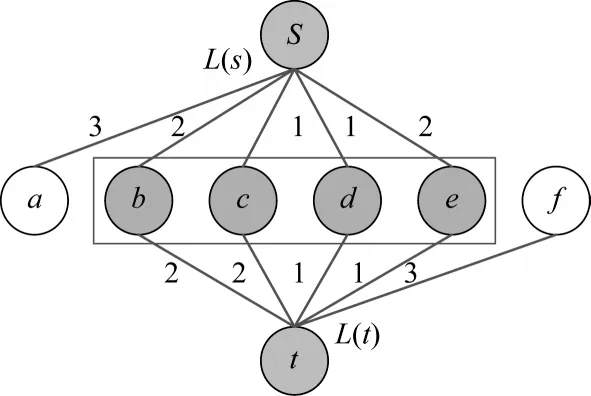
图1 二跳覆盖标记方案示例Fig.1 Example of 2-hop cover labeling scheme
在图1 中,先计算两者的标记L(s)和L(t),再选取具有公共顶点的路径计算最短距离,计算公式为:min{δ+δ'|(u,δ)∊L(s),(u,δ')∊L(t)}。
该实例的具体计算过程如下:
如果L(s) 和L(t) 不存在相同顶点,则定义Query(s,t,L)=∞。
2)伪随机函数和伪随机排列。伪随机函数Function:{0,1}λ×{0,1}*→{0,1}*是一个多项式时间可计算函数,任何概率多项式时间敌手都无法将其与随机函数区分。当伪随机函数是双射时,则称其为伪随机排列。
3)字典。安全索引结构是以字典数据结构为基础构建的,一个字典I以(kkey,vvalue)对的形式进行存储。给定I中的一个kkey,其对应vvalue可在O(1)时间内返回。用I[kkey]:=vvalue表示字典I中通过kkey标记的值vvalue,若kkey在I中不存在,则返回⊥。
3 系统模型和定义
本节设计一个基于路径标记的图数据外包计算方案,实现高效、安全的密文图数据最短距离查询。
3.1 系统模型
系统构造图数据隐私保护外包计算模型涉及到3 个实体,即数据所有者(Data Owner,DO)、可信的查询请求者(Query Requester,QR)和半诚实的云服务提供商(Cloud Service Provider,CSP)。西部地区的图数据存储中心作为数据所有者,东部发达地区的图数据服务企业作为查询请求者,低成本的图数据存储中心无法提供高效快速的计算,第三方云服务商应运而生。此时查询请求者是可信的,且不会与第三方云服务提供商合谋。图2 所示为密文图数据上最短距离外包计算模型。

图2 密文图数据上最短距离外包计算模型Fig.2 Outsourced computation model of the shortest distance over encrypted graph data
图2 中每个实体的描述如下:
1)数据所有者。数据所有者在本地将拥有的原始图数据预处理生成标记信息,并对标记信息加密,得到密文安全索引结构。然后将图数据安全索引结构发送至云服务提供商,并将部分密钥发送至查询请求者。在查询阶段,数据所有者和云服务提供商协同执行一个安全比较协议。
2)查询请求者。在查询阶段,查询请求者根据最短距离查询请求,使用令牌生成算法对请求节点进行加密,将查询令牌发送给云服务提供商。在查询执行阶段,云服务提供商计算出密文查询结果,并将其返回给查询请求者。在解密阶段,查询请求者对密文最短距离结果进行解密计算,得到真实最短距离。
3)云服务提供商。假设系统模型中CSP 是诚实但好奇的,能诚实地执行计算协议,但在协议执行过程中会对数据所有者、查询请求者等用户的数据好奇,甚至窥探或推断隐私数据。在执行最短距离查询阶段,CSP 根据图数据的加密安全索引结构及查询令牌进行计算,在比较最短距离时与数据所有者协同执行安全比较协议,得出密文结果后返回给查询请求者。
系统模型包括4 个阶段,即预处理阶段、加密阶段、最短距离查询阶段和解密阶段。在预处理阶段,数据所有者将本地原始图数据G预处理生成标记信息。在加密阶段,数据所有者使用加密方案对标记信息加密生成图数据的密文索引结构I,并将I发送给CSP,将加密图数据的部分密钥发送给查询请求者,以便计算查询令牌和密文结果解密。在最短距离查询阶段,为查询任意节点间的最短距离,查询请求者根据查询节点(s,t∊G)计算对应的查询令牌τs,t,并将查询令牌提交给CSP;CSP 根据图数据的密文安全索引结构I和查询令牌τs,t进行最短距离计算。CSP 具体查询计算过程为:首先,根据查询令牌τs,t解析对应的查询节点;其次,通过安全索引结构I计算密文距离集合,协同数据所有者执行安全比较协议并获取最小值Ds,t;最后将密文查询结果Ds,t返回给查询请求者。在解密阶段,查询请求者将密文最短距离结果Ds,t解密为明文最短距离结果ds,t。
3.2 形式化定义
本节结合图2 所示的模型提出基于二跳覆盖修剪标记的图数据隐私保护最短距离外包查询计算框架的形式化定义,实现加密图数据上保护隐私的最短距离查询。
定义1(Graph-SPD)图数据隐私保护最短距离外包查询计算框架由多项式时间算法构成,表达式为{prunedBFS,KeyGen,Encrypt,TokenGen,Dist Query,Decrypt},其中:{L(v)}v∊G←prunedBFS(G),即数据所有者在本地对原始图数据G进行预处理。该算法基于二跳覆盖标记生成原始标记后执行广度优先遍历修剪策略,输出最终标记集合{L(v)}v∊G。
(K,pk,sk)←KeyGen(λ):由数据所有者执行该密钥生成算法。算法以一个安全参数λ作为输入,输出密钥(K,pk,sk)。
I←Encrypt(K,pk,{L(v)}v∊G):数据所 有者执行该加密算法。数据所有者输入密钥K,pk和标记集合{L(v)}v∊G,输出安全索引结构I。
τs,t←TokenGen(K,q):查询请求者执行查询令牌生成算法,根据查询请求q=(s,t)及密钥K,生成查询令牌τs,t并输出发送给CSP。
Ds,t←DistQuery(I,τs,t):CSP 执行最 短距离查询算法,以安全索引结构I和查询令牌Ds,t←DistQuery(I,τs,t)为输入,解析查询令牌并结合索引结构计算密文最短距离Ds,t。
ds,t←Decrypt(sk,Ds,t):查询请求者执行解密操作算法。该算法以密钥sk和密文最短距离结果Ds,t作为输入,输出明文距离ds,t。
3.3 安全定义
定义2(自适应语义安全)给定一个Graph-SPD 框架{prunedBFS,KeyGen,Encrypt,TokenGen,DistQuery,Decrpt},设在执行加密和查询的过程中泄露信息所对应的泄露函数是L1和L2,同时设置λ为安全参数,挑战者C、敌手A和模拟器S,定义游戏RealC,A(λ)和IdealC,A,S(λ)。
RealC,A(λ):敌手A构造一个图G并将其转发给C。C首先对图G进行预处理,基于二跳覆盖生成原始标记并对其修剪计算,生成标记集合{L(v)}v∊G;然后,执行密钥生成算法(K,pk,sk)←KeyGen(λ);最后,执行加密算法I←Encrypt(K,pk,{L(v)}v∊G),对标记集合中的节点和距离加密,得到一个安全索引结构I并返回给A。A自适应发出最短距离查询请求q=(s,t),A首先计算该请求的查询令牌τs,t←TokenGen (K,q),然 后A结合I和τs,t执行密 文最短 距离查 询Ds,t←DistQuery(I,τs,t),最后A返回(b) ←{0,1}并作为游戏输出。
IdealC,A,S(λ):敌手A构造一个图G并将其转发给C。C将泄露函数L1(G)的输出转发给模拟器S,S模拟一个安全的索引结构I*返回给A。给定I*,A自适应地发出最短距离查询。对于每个最短距离查询q=(s,t),C将泄漏函数L2(G,q)的输出发送给S,S模拟生成相应的查询令牌发送给A。A计算密文最短距离,得到结果并返 回b←{0,1}作为游戏输出。
为进一步提供方案的可证明安全性,对该方案的泄露函数L1和L2进行描述并定义自适应(L1,L2)-安全。
在加密过程中,通过观察密文安全索引I的长度,敌手可获取修剪后标记中(u,δuv)对的总数。给定一个图G,定义泄露函数。在对查询请求q=(s,t)进行密文最短距离查询过程中,敌手获取L(s)和L(t)中各自的(u,δuv)对数,同时通过令牌和伪随机函数计算模糊存储位置和标识符,敌手学习L(s)和L(t)的公共节点数nnum。在多次查询请求q=(s1,t1),(s2,t2),…,(sq,tq)中,敌手可通过学习多次查询,获取查询节点间是否被重复查询以及重复信息rrep。由给定的图G和查询序列q,定义泄露函数L2(G,q)=(nnum,rrep)。
定义3(自适应(L1,L2)-安全)由定义1 给出的Graph-SPD 方案,其泄露函数L1和L2的定义如前所述。若对于所有的概率多项式时间的敌手A,可以构造一个满足概率多项式时间的模拟器S,使|Pr[RealC,A(λ)=1] -Pr[IdealC,A,S(λ)=1]| ≤negl(λ),其中:negl(·)是一个可忽略的函数,则该密文图数据精确最短距离外包计算方案是自适应(L1,L2)-安全的,能够抵抗自适应选择查询攻击。
4 方案设计
本节基于加法同态、部分同态加密及两个特定的伪随机函数f和g提出基于二跳覆盖标记的图数据最短距离查询外包计算方案,分为3 小节对方案中预处理阶段、加密阶段、最短距离查询阶段进行详细阐述和具体算法的实现与设计。
4.1 预处理阶段
为快速应答最短距离查询,可以通过基于标记的方法进行处理。其中,一种简单的标记方法是:对于每个节点v∊V,从v开始进行广度优先搜索并存储v与其他所有节点之间的距离,即预先计算标记L(v)。相较于直接在图上进行最短距离查询,预先计算标记并在标记上进行查询的计算效率更高。二跳覆盖标记已广泛应用于基于标记的距离查询方案[13]。受修剪地标标记(Pruned Landmark Labeling,PLL)[30]的启发,本文方案不直接对原始图数据或原始二跳覆盖标记数据进行加密外包,而是利用基于二跳覆盖标记方法对原始图数据在广度优先搜索(Breadth First Search,BFS)期间进行修剪,通过修剪预处理构造原始图数据的修剪二跳覆盖标记,以减小明文标记数量的规模和密文图数据安全索引结构的尺寸,提高后续图数据加密和最短路径查询的效率。
在图数据预处理阶段对标记修剪的工作原理为:在修剪BFS 过程中,给定一个预先定义图G中所有节点的标记顺序(v1,v2,…,v|V|),按照标记顺序依次执行广度优先搜索修剪策略。在以vk为根节点的修剪过程中,使用δ[u]表示vk和u之间的距离,从空标记L'0开始,L'k-1是第k-1 次执行修剪BFS 生成的 标记,根据L'k-1计算L'k,即以vk为根节点执行第k次修剪生成的标记。若Query(vk,u,L'k-1)≤δ[u],则对顶点u进行修剪并不再从u遍历其他边,L'k(u)=L'k-1(u),即不添 加(vk,δ[u]),否则设 置L'k(u)=L'k-1(u)∪ {(vk,δ[u])},并继续从u开始遍历到其他边。标记{L'0,L'1,…,L'k-1,L'k}共同构成标记集合{L(v)}v∊G,标记中存储图数据所有节点与其邻接节点的信息,包含邻接节点名称和距离值。
为了进一步阐明图数据预处理阶段的标记数据修剪过程,图3 给出一个具体的广度优先搜索修剪策略实例,其中斜线节点表示根节点,网格节点表示已访问并标记过的节点,竖线节点表示已访问但修剪的节点,阴影节点表示已经用作根的节点。图3中,初始节点顺序为v=(1,2,…,n),按照该顺序依次进行修剪。以原始图数据作为初始示例,执行二跳覆盖标记[图3(a)];按照顺序从节点1 进行第1 次修剪BFS,此时以节点1 为根节点利用二跳覆盖访问其余节点,完成所有节点的访问[图3(b)],无任何节点被修剪掉;然后,按照顺序从节点2 执行第2 次修剪策略[图3(c)],此时节点1 已用作根节点,以阴影表示,以节点2 为根节点,利用二跳覆盖能够访问的节点用网格表示,但以节点2为根节点时节点6与节点12未能访问,在以节点1 为根节点时节点6 及节点12却能被访问,又因为Query(2,6,L'1)=dG(2,1)+dG(1,6)=3=dG(2,6),故修剪节点6 并不再从此顶点遍历到其他边,同理修剪节点12;此后,逐节点执行修剪策略,随修剪策略执行次数的增加,访问节点逐渐减少,最短距离的搜索空间也逐渐减少,从而提升查询效率[图3(d)、图3(e)];最后,以节点12 为根节点执行第12 次修剪策略,结束所有修剪工作。

图3 广度优先搜索修剪策略示例Fig.3 Example of breadth first searching pruning strategy
结合图数据预处理阶段的原理和实例,算法1给出了具体的图数据预处理修剪过程。
算法1prunedBFS


在算法1 所示的图数据预处理阶段中,prunedBFS 算法以图G作为输入,以修剪后的最终标记集合{L(v)}v∊G作为输出。具体而言,算法1 对图G中的每个节点v遍历并进行广度优先搜索,并在广度优先搜索期间进行修剪,将其邻接节点和距离信息添加到对应的标记中。算法1 在从节点vk出发进行广度优先搜索修剪时,使用δ[v]表示vk和v之间的距离,根据L'k-1计算L'k(算法1 中第3 行~第6 行),其中:L'k-1是指前序以节点vk-1执行第k-1 次广度优先搜索修剪策略产生的标记;L'k为以vk为根节点执行第k次修剪生成的标记。Query(vk,u,L'k-1)表示使用L'k-1中的标记查询vk和u之间的距离。修剪过程中结合队列Q进行存储删除,若Query(vk,u,L'k-1)≤δ[u],则标记(vk,δ[u])被修剪(算法1 中第7 行~第11行),此时标记已覆盖vk和u之间的最短距离;否则,遍历顶点u的所有邻接节点所对应的边并继续计算最短距离,其中NG(v)为顶点v∊V的邻接节点集合(算法1 中第12 行~第14 行)。最终,递归标记{L′0,L′1,…,L′k-1,L′k}共同构 成标记集合{L(v)}v∊G。由算法1 可知,在处理大规模图数据时,其构建标记的时间和空间复杂度分别为O(|V||E|)和O(|V2|)。
4.2 加密阶段
为保证外包计算过程中标记集合的隐私,数据所有者对原始图数据进行预处理并生成标记集合后,需要进一步对标记集合进行加密。该阶段主要涉及两个步骤:密钥生成及标记加密。
密钥生成算法结合安全参数生成密钥。选择一个安全参数λ作为算法输入,从伪随机函数域中均匀随机生成伪随机函数值K←{0,1}λ,同时生成一个密钥对(pk,sk),然后将部分密钥K,sk发送至查询请求者。具体过程如算法2 所示。
算法2KeyGen

生成密钥后,数据所有者对根据算法1 得到的标记集合{L(v)}v∊G进行加密,构造安全密文索引结构I。在标记加密过程中,首先对标记集合的元素(u,δuv)∊L(v)依次加密:数据所有者对节点标识符u使用伪随机函数f进行编码U:=f(K,u||0)),对距离值δuv使用部 分同态 加密进 行密文处理Du,v←SWHE.Enc(pk,δuv);其次,先对每个节点v∊G计算其对应的键,即令牌Tv:=f(K,v||1)),同时为节点v对应的所有邻接节点标识集合构造索引Lv并设置内部键值对,即子令牌kkey,u,v:=f(cctr,v,U)⊕Tv,其中ctr为计数器;再次,利用多重索引并结合伪随机函数模糊存储位置,即eenc,u,v:=g(cctr,v,f(K,u||2))),使各个边之间难以区分;然后,为构成安全的索引结构,将密文节点和密文距离值与多重索引保护值进行异或处理,生成不可区分的标识值Hu,v,避免泄露查询节点的存储位置和真实值;最后,安全索引结构I以(Tv,Lv)对形式存储密文标记。
具体标记加密如算法3 所示。
算法3Encrypt


在算法3 中,数据所有者对图数据的标记集合进行加密,遍历节点进行加密操作(算法3 中第3 行~第15 行),包括节点u伪标识加密和距离值δuv加密(算法3 中第6 行~第7 行),根据节点生成令牌(算法3 中第4 行)及其对应的子令牌(算法3 中第8 行),结合伪随机函数和多重索引进行异或操作,生成不可区分的节点标识,最终由令牌和密文标记集合共同构成安全索引结构I(算法3 中第9 行~第14 行),并将其发送给CSP。
算法3 的时间复杂度为O(md),其中:m为图数据的节点总数;d是经过修剪后单个节点的标记条目数量。在标记加密过程中,逐节点找寻邻接节点构成原始标记,原始标记与节点的度相关,通过修剪原始标记可获得修剪后的标记集合,修剪后各节点的标记数量大幅减少,单个节点的标记条目d远小于该节点的度。随机选定图数据集,边数为顶点数的n/m倍,在通常情况下d 密文图数据的最短距离查询阶段使用令牌生成算法和距离查询算法,由数据所有者、查询请求者和CSP 交互完成。首先,令牌生成算法中查询请求者对查询节点计算出查询令牌,根据查询请求q=(s,t)及密钥K生成查询令牌τs,t,其中查询令牌τs,t由Ts和Tt构成,并将令牌τs,t发送给CSP。其次,距离查询算法中CSP 对收到的查询令牌τs,t进行解析,并根据安全索引结构I计算距离集合,结合数据所有者执行安全比较协议,获取密文最短距离结果。 为便于理解,本节分为3 个小节,将在第4.3.1 节简单介绍查询令牌生成算法,在第4.3.2 节阐述距离查询算法,在第4.3.3 节提出支撑距离查询算法执行的安全比较协议。 4.3.1 查询令牌生成算法 算法4TokenGen 在算法4 中,查询请求者根据最短距离查询请求q=(s,t)及密钥K,生成对应节点令牌并构成查询令牌τs,t(算法4 中第1 行~第4 行)。算法执行完后,查询请求者将τs,t发送给CSP。 4.3.2 距离查询算法 在距离查询算法中,CSP 首先对收到的查询令牌τs,t进行解析,获取到密文源点令牌Ts及密文终点令牌Tt,并根据节点令牌计算其对应的子令牌kkey,u,s及kkey,u,t。其次,根据子令牌查询邻接节点标识集合索引Lv中对应的密文节点和边长,并将两者对应的(U,Du,v)对存储在集合L(s)与集合L(t)中。再次,CSP基于标记集合L(s)与L(t)筛选其中存在包含公共节点的(U,Du,v)对。筛选过程为:遍历标记集合L(s)与L(t)中的每个条目,如果在L(s)中存在Ui,在L(t)中存在Uj,满足Ui==Uj(即两个顶点相同),此时存在包含公共节点Ui==Uj的(Ui,Dsi)和(Uj,Djt);然后,CSP计算两者距离和Di=Add(Dsi+Djt)并作为新的距离值。由于采用加法同态密码系统加密距离值,故可对密文距离值执行相加操作。最后,在同态相加后基于CSP 与数据所有者的安全比较协议计算距离最小值,通过对候选距离集合中的所有整数进行比较来查找最小值,并将密文最短距离值Ds,t作为最终结果返回给查询请求者。 安全比较协议计算距离最小值的具体内容如第4.3.3 节所示。若存在相同最短距离,则将存在多个候选结果,忽略路径返回密文最短距离值作为最终结果返回。具体的距离查询算法如算法5 所示。 算法5DistQuery 在算法5 中,CSP 首先计算令牌对应的密文标记集合:将τs,t解析为节点令牌Ts和Tt(算法5 中第1行),根据当前节点,令牌Ts计算该节点与邻接节点的子令牌kkey,u,s,结合模糊存储位置eenc,u,s计算节点标识值Hu,s,进而结合异或操作推出密文标记(U,Du,s),将所有标记存储至集合L(s)中(算法5 中第3 行~第11 行)。同理计算节点令牌Tt对应的密文标记集合L(t)(算法5 中第12 行)。其次,筛选标记集合L(s)与L(t)包含公共节点的(U,Du,v)对,若节点相同,则根据加法同态加密执行密文距离值相加操作,否则遍历标记集合L(s)中的邻接节点,继续筛选及判断邻接节点的标记集合L(i)与L(t)的公共节点,进而计算出源节点s至目的节点t的所有连通的密文距离值,并存储至密文距离集合DDist中(算法5 中第13 行~第19 行)。最后,结合数据所有者和CSP 之间的安全比较协议,计算密文距离最小值Ds,t并返回给查询请求者(算法5 中第20 行~第24 行)。 此外,算法5 的时间复杂度为O(d),其中d为单个节点的标记条目数量。在最短距离查询过程中,通过解析已知的查询令牌,然后确定源节点令牌和目的节点令牌,在安全索引结构中搜索查询节点令牌对应的标记,进而在标记中寻找共同节点并计算距离集合。由于查询令牌确定,因此可从安全索引结构中直接计算标记,至多执行d次比较就能得出公共节点,进而从公共节点中计算距离集合。查询最短距离结果后返回结果,在此过程中无需额外存储,仅返回密文距离值,故空间复杂度为O(1)。 查询请求者接收到CSP 发送的密文最短距离Ds,t后,仅需密钥sk对其进行解密即可得到明文最短距离ds,t,故对解密阶段省略描述。 4.3.3 安全比较协议 假定实体间不合谋,安全比较协议由CSP 和数据所有者共同执行。CSP 可以通过使用混淆电路与同态加密相结合的方案来实现两个密文距离值的比较。受混淆电路块[31]的启发,安全比较协议中安全比较电路由CMP 电路和SUB 电路构造,CMP 电路用于位比较,SUB 电路用于位减,两者均采用自由异或技术。该协议中安全比较电路的具体实现如图4所示。 图4 密文距离值安全比较电路Fig.4 Secure comparison circuit for encrypted distance values 在实际密文距离值比较过程中,CSP 拥有查询节点间的密文距离集合DDist={[D1],[D2],…,[Dn]},数据所有者拥有密钥。安全比较协议基于朴素最小值算法,CSP 依次比较DDist集合中的密文距离值,获取最短距离。假设DDist集合中所有值均位于范围2l内,即所有密文距离值是l位整数。CSP 不会直接向数据所有者发送密文距离值,而是通过同态加密特性利用一个k位随机数ri对密文距离值进行掩码处理,即[Di+ri]=[Di]∙[ri],其中k是一个 参数且k>l。掩码通过对整数执行加法操作进行统计隐藏,对l位整数[Di]和k位整数[ri]来说,发送[Di+ri]可以为密文距离值提供约2l-k的统计安全性。选择合适的k,可以使得统计差异变得任意小。此时数据所有者输入随机数[r1]和[r2],CSP 输入[D1+r1]和[D2+r2],在通过安全比较电路后,输出位b表示比较结果,如果[D1]>[D2],则b=1,否则b=0。逐密文值进行比较最终得出最短距离。 具体密文距离的安全比较协议如协议1 所示。 协议1安全比较协议 步骤1CSP 整理密文距离值集合DDist={[D1],[D2],…,[Dn]},并依次选取两个密文距离值[D1]和[D2]; 步骤2数据所有者利用同态性选取随机数ri并输入对应的随机数[r1]和[r2],将其发送至安全比较电路; 步骤3CSP 利用随机数[r1]和[r2]对密文距离值[D1]和[D2]进行掩码处理,即输入[D1+r1]和[D2+r2]至安全比较电路; 步骤4通过安全比较电路后,输出位b表示比较结果,即,选出最小值后继续与集合中的密文距离值进行比较; 步骤5最终将Ds,t=min{DDist}=min{[D1],[D2],…,[Dn]}作为结果返回。 协议1 中密文距离值的安全比较协议采用朴素最小值比较,基于安全比较电路依次对密文距离集合中的元素进行比较,最终获取密文最短距离。 本节对第4 节所提方案进行安全性分析,分别分析方案中图数据加密系统的安全性和密文图数据最短距离外包计算方案的安全性。 定理1本文所提密文图数据精确最短距离计算方案在随机预言模型下满足选择明文攻击不可区分的安全性(即IND-CPA 安全)。 证明: 假设存在任何多项式时间的敌手A 攻击密文图数据精确最短距离的计算过程,可以构建挑战者ℬ以可忽略的概率保证IND-CPA 安全。 敌手A 考虑以下攻击实验:在初始化阶段,挑战者ℬ 产生加密系统,敌手A 获得系统的密钥。 模拟密文最短距离查询,敌手A 为获取加密图数据与标记的信息,输出查询请求,其中包含两个不同的节点信息,即q=(s,t);然后对其进行加密,得到查询令牌,并对当前查询请求进行结果询问。 敌手A 继续对任意节点执行最短距离计算询问,根据查询令牌和安全索引结构,判断当前查询节点是否存在,若存在,则依据查询令牌和安全索引结构计算密文最短距离Ds,t,否则返回空值,使其重新发起查询请求。 最后敌手A 停止询问并输出一组查询请求q*=(s*,t*)的猜测密文最短距离结果D's*,t*,根据(s*,t*)的查询令牌τs*,t*可得真实密文最短距离结果Ds*,t*,若Ds*,t*=D's*,t*,则敌手A 攻击成功。 敌 手 A 的优势 可定义 为 :AOPE,A(k)=,其中k为用于加密方案中的安全参数。 设方案存在一个可忽略的函数negl(k),使得,即保证该方案在随机预言模型下以概率negl(k)满足IND-CPA 安全。 定理2如果对称加密算法、伪随机函数是安全的,则所提出的基于二跳覆盖标记的图数据最短距离外包计算方案实现(L1,L2)安全。 证明: 在查询请求者发出查询令牌之前,敌手A 仅可获取安全索引结构,并进一步推断方案在加密阶段中泄露图的相关信息。具体而言,敌手A 通过观察加密索引的长度可得二跳覆盖标记索引中(u,δuv)对的数量,即给定 图G可得。在查询阶段,当查询请求者发出查询请求q=(s,t)时,敌手A 了解到在L(s)和L(t)中的共同顶点数量nnum。由于伪随机函数是确定的,因此敌手A 通过观察标记两个查询q1=(s1,t1)和q2=(s2,t2),能够识别两者间的等价关系。给定图G和查询序列q=(s1,t1),(s2,t2),…,(sp,tp),可 得L2(G)=(rrep,q,nnum),其中rrep,q存储查询顶点的重复信息,判断顶点是否被重复查询;nnum为存储共同顶点数量的数组。 在游戏中构造一个模拟器S,使用L1,L2模拟一个适当的索引I*并根据查询(s,t)生成查询令牌。模拟器S根据查询令牌计算索引I*中对应的距离值,模拟一组二跳覆盖标记中的(u,δuv)对的距离值集合,即,判断在集合C*中的大小关系,然后模拟器S通过索引I*模拟计算t个节点标识符,并将插入到标记集合中。当中的共同节点数等于nnum时,模拟器S删除重复的标记并将标记重新表示。 由于安全索引结构的构造使用伪随机函数、部分同态加密、多重索引等,每个节点的密文值均不相同,且索引中距离值的加密使用长度为128 的安全参数难以破解安全索引结构,因此方案是实际安全有效的。 敌手A 伪造查询条件和密文索引结构,由于对称加密和伪随机函数两个密码原语是安全的,故在查询请求前与查询过程中,索引I和I*的距离计算过程和结果是不可区分的,即任意多项式时间敌手A对于RealC,A(λ)和IdealC,A,S(λ)具有不可区分性,因此方案实现(L1,L2)安全。 本节首先将本文提出的加密图数据最短距离查询外包计算方案与文献[17]、文献[20]、文献[21]、文献[22]、文献[25]方案进行分析对比,然后通过在8 个公开的真实数据集上进行实验,验证本文方案性能。 本文所提出Graph-SPD 方案的开销主要在加密阶段与查询阶段。加密阶段的时间开销和空间开销取决于二跳覆盖标记生成标记的数量,其时间复杂度为O(md),空间复杂度为O(md)。在查询阶段对密文索引结构查询最短距离时依据查询顶点检索安全索引结构中对应的标记,其时间复杂度为O(d),空间复杂度为O(1)。 本文所提的Graph-SPD 方案实现了加密图数据上的精确最短距离查询,其基于二跳覆盖标记和修剪策略生成标记集合,利用加法同态加密、伪随机函数、部分同态加密等密码原语来加密标记集合并生成相应的密文安全索引结构,根据查询令牌在索引中计算标记,找寻公共节点对距离值进行同态加法计算,进而比较距离集合实现最短距离查询。该方案与现有的加密图数据外包计算方案具有明显差异,如表2所示,其中:m为节点数;n为边数;u为结构图的节点数;η为构造结构图的尺寸;l为标记中的条目数;d为安全索引结构的标记长度。由表2 可知,文献[17]、文献[20]、文献[21]方案均实现了密文图数据的近似最短距离查询,其中文献[17]方案采用距离预言和同态加密的方式处理原始图数据,在安全性方面存在泄露节点总数和最大距离值的问题。文献[20]、文献[21]方案均采用二跳覆盖标记存储距离值,其中:文献[20]方案使用保序加密以保证距离值之间的顺序信息,进而计算近似最短距离,该方案存在泄露顺序信息、索引长度、重复信息的问题;文献[21]方案聚焦带约束的最短距离查询问题,其基于同态加密实现隐私与效率共存的近似最短距离计算,在安全方面存在泄露图数据的节点数量、边数量和公共顶点信息的问题。以上3 个方案均为提高计算效率而降低了查询精度,而本文方案在保证查询计算效率[即密文查询时间复杂度O(d)]的前提下实现了密文图数据上精确最短距离查询,提高了查询精度。 表2 加密图数据下不同外包计算方案的对比 Table 2 Comparison among different outsourced computation schemes under encrypted graph data 本文和文献[22]、文献[25]均设计了精确最短距离查询方案,其中:文献[22]方案采用邻接表实例化原始图数据,能保证查询精度,然而查询时间复杂度较高,邻接表数量和重复信息也容易被泄露;文献[25]方案采用二跳覆盖标记和同态加密方法实现带约束的精确最短距离查询,却无法直接应用于无约束的精确最短距离查询,同样在查询过程中容易泄露查询的重复信息。相较文献[22]、文献[25]方案,本文的加密和密文查询机制不同,因此本文提出基于修剪二跳覆盖标记和加法同态加密的图数据精确最短距离查询外包计算方案。此外,在安全性方面,相较(L1,L2,L3)安全[22]或CQA2 安全[25],本文方案更加安全,能够同时满足IND-CPA 安全和(L1,L2)安全。在计算效率方面,相较于文献[22]方案,本文方案在加密阶段采用了不同的数据结构处理原始图数据。文献[22]方案生成3 个字典加密图数据,时间复杂度和空间复杂度均为O(m+n),而本文方案逐节点对其标记进行加密,时间复杂度和空间复杂度均为O(md);在查询阶段,文献[22]方案使用斐波那契堆加速Dijkstra 算法,同时添加辅助结构存储历史查询,获得了O(m+nlogan) 的时间复杂度和O(m)的空间复杂度,本文方案直接对查询节点的标记计算最短距离并在查询结束后仅返回密文距离,因此时间复杂度为O(d),空间复杂度为O(1)。相较于文献[25]方案,本文方案在加密阶段不需要对所有顶点的全部标记进行加密,将计算复杂度和空间复杂度都从文献[25]的O(l)提升为O(d);在查询阶段本文方案无需计算所有节点的标记,通过找寻修剪后的标记集合间共同节点得出距离值,使计算复杂度从O(n)提升为O(d),空间复杂度保持O(1)不变。 为进一步验证本文所提Graph-SPD 方案的实际计算效率,本文在不同的公开真实数据集上进行实验,并与文献[22]、文献[25]所提出的密文图数据的精确最短距离计算方案进行实验对比。由于文献[22]的方案无标记处理这一预处理过程,所以标记处理生成的标记数量和时间开销对比仅在本文方案和文献[25]方案之间进行,图数据加密、查询令牌生成、最短距离查询、查询结果解密等时间开销对比在3 个方案之间进行。 6.2.1 实验设置 为了使实验结果具有客观性,本文选取与文献[22]、文献[25]部分相同的真实图数据集来测试方案性能。实验均由C++编程语言实现,实验环境为Ubuntu 18.04 Linux X86 64 位操作系统,客户端配置为Intel®CoreTMi5-7200U(2.70 GHz)CPU,12 GB RAM,服务器配置为2.7 GHz Intel Xeon CPU 8 核、16 GB RAM。伪随机函数和对称密钥算法由哈希运算消息认证码(Hash-based Message Authentication Code,HMAC)和高级加密标准(Advanced Encryption Standard,AES)实例化,安全参数设为128 bit。 实验选用SNAP 网站公开的图数据集作为实验数据,表3 总结了所选的8 个数据集的主要特征,包含数据集名称、图类型、节点数和边数。在表3 中,数据集ego-Facebook(简称Facebook)来自Facebook的社交网络,是由用户好友列表组成的特征集合;数据集p2p-Gnutella(简称Gnutella)是Gnutella 对文件共享网络的快照序列,表示网络拓扑中的主机连接关系;数据集ca-AstroPh(简称AstroPh)是涵盖提交到Astrophysics 类别的作者论文之间的合作网络;数据集email-Enron(简称Enron)记录了与安然电子邮件地址往来的邮件通信,构成电子邮件通信网络;数据集ca-CondMat(简称CondMat)是凝聚态物质研究相关的论文作者之间的学术合作网络;数据集loc-Brightkite(简称Brightkite)是由用户签到数据构成的社交网络;数据集soc-Slashdot(简称Slashdot)是由新闻网站中特定用户构成的社交网络;数据集email-EuAll(简称EuAll)是欧洲研究机构对收发的电子邮件匿名化处理生成的电子邮件网络。与文献[22]、文献[25]相同,本文在实验过程中为表3 中所有图数据的边分配了随机的距离值,范围为[0,10],精度为0.01。在实验过程中,为保证实验结果的客观性,在预处理、图数据加密、查询令牌生成、最短距离查询和查询结果解密这几个阶段,分别进行30 次重复实验,将平均时间开销作为实验结果数据。在最短距离查询阶段,采用中心极限定理的思想,在不同数据集中随机选取5 组顶点对进行最短距离查询,每组执行30 次查询,得到随机抽样查询时间开销的平均值,即最短距离查询平均时间。 表3 本文数据集的主要特征 Table 3 Key characteristics of data sets in this paper 6.2.2 实验结果 本文方案与文献[25]方案均在对原始图数据进行加密之前分别利用二跳覆盖标记处理机制对图数据进行预处理,生成原始图数据的标记集合,以提高图数据加密、最短距离查询等操作的效率。本文方案与文献[25]方案在预处理阶段相同数据集下生成的标记数量以及花费的时间有很大差异,图5 所示为标记数量及标记生成时间开销对比,其标记数量对比如图5(a)所示,标记生成时间开销对比如图5(b)所示。 图5 标记数量及标记生成时间开销对比Fig.5 Comparison of the number of labels and the time overhead of label generation 图5 表明,本文方案相比文献[25]方案在不同数据集上生成的标记数量降低46.74%~60.00%,且随着数据集的规模增大,标记数量的减少幅度愈大;在不同数据集上生成标记的时间开销上,相比于文献[25]方案,本文方案的时间开销增加了9.91%~30.44%,时间开销的增加与图数据规模、结构复杂程度相关。 本文方案在图数据预处理的标记生成数量上有巨大优势,这是由于文献[25]方案仅利用二跳覆盖标记方法构建标记集合,其生成的标记数量与图的节点规模相同;而本文方案采用修剪二跳覆盖标记构建标记集合,在生成标记时,逐节点进行遍历并执行广度优先搜索修剪策略,减少由二跳覆盖标记生成的原始标记数量。 本文方案的标记生成增加了额外的时间开销,这是因为本文方案在二跳覆盖标记的基础上进行广度优先搜索修剪策略,而标记生成时间包括了标记修剪时间。增加的时间开销比例与图数据规模和结构复杂程度相关,规模越大、越复杂的图数据其广度优先搜索策略的开销越大。此外,如前所述,文献[20]方案采用邻接表实例化原始图数据,未生成标记,故不对其进行比较。 在图数据加密阶段,文献[22]方案直接对图数据进行加密,本文方案和文献[25]方案分别对生成的标记信息进行加密,构造安全索引结构。3 个不同方案的加密时间开销对比如图6 所示。 图6 图数据加密时间开销对比Fig.6 Time overhead comparison of encrypted graph data 由图6 可知,3 个方案的加密时间开销均与图数据的规模呈线性相关,时间开销随图数据规模的增加而增加。其中本文方案具有明显优势,加密时间开销比文献[25]方案降低了13.04%~24.24%,比文献[22]方案降低了23.08%~34.21%;本文方案在所有图数据上的加密时间开销均在可接受范围内,即使原始图数据或标记数量规模接近百万,加密时间也仅需120 s。 本文方案在加密时间开销方面具有显著优势的主要原因是,本文方案对图数据生成的原始标记采用广度优先搜索修剪策略进行修剪,使标记数量大幅减少,降低了加密阶段需要加密的明文长度,提高了图数据的加密效率。文献[25]方案直接对原始标记进行加密处理,虽然标记数量与原始图数据的邻接矩阵相比大幅减少了明文长度,但该方案需要加密原始图数据对应的所有标记,故仍有优化空间。文献[22]方案需要对邻接表实例化后的图数据进行加密,邻接表实例化构造复杂,需要加密的明文长度最长,因此在3 个方案中该方案加密时间开销最高。 在查询令牌生成阶段,本文方案与文献[22]、文献[25]方案的查询请求者均会发出查询请求,并对查询请求加密生成查询请求令牌,3 个方案的查询令牌生成的时间开销对比如图7 所示。由图7 可知,3 个方案中的令牌生成时间开销均为常数级,约为0.4 ms。这是由于3 个方案中的查询请求模式一样,即发出一个顶点对之间的最短距离查询请求,在生成查询令牌时仅需要对待查询的2个顶点进行加密。 图7 生成查询令牌的时间开销对比Fig.7 Time overhead comparison of generating query token 在最短距离查询阶段,CSP 根据查询请求者提交的查询令牌,查询两点之间的密文最短距离,本文与文献[22]、文献[25]方案的最短距离查询时间开销对比如图8 所示。图8 表明,3 个方案的最短距离查询时间开销均与图数据的规模大小和结构复杂程度正相关,规模越大、复杂程度越高,所需要的时间开销越大。其中,本文方案的最短距离查询时间开销最小,相比文献[22]、文献[25]方案具有巨大优势,相比文献[22]方案降低了90% 以上,相比文献[25]方案降低了36.44%~46.13%。 图8 最短距离查询的时间开销对比Fig.8 Time overhead comparison of the shortest distance querying 本文方案的最短距离查询时间开销显著降低的原因是文献[22]方案为实现精确最短距离查询设计构造了斐波那契堆,增加了时间开销,同时为支持图数据的动态更新,该方案构建了辅助数据结构存储历史查询的查询结果,若当前节点未曾查询,则需重新计算,故综合而言,文献[22]方案最短距离查询时间开销较高。文献[25]方案基于部分同态加密进行带约束的精确最短距离计算,计算代价的约束以及准确性的影响使得查询效率降低,查询时间增加。而本文方案基于加法同态加密并结合标记修剪策略执行精确最短距离计算,一方面由于密文长度相比文献[22]、文献[25]方案得到了大幅降低,因此缩小了密文数据上的查询搜索空间;另一方面由于在密文图数据上保留了供最短距离查询的邻居信息,因此在进行密文距离对比时效率更高。 在密文结果解密阶段,本文方案与文献[22]、文献[25]方案中的查询请求者只需使用密钥对密文距离值解密,其密文结果解密的时间开销对比如图9所示。 图9 密文结果解密的时间开销对比Fig.9 Time overhead comparison of decrypting ciphertext results 由图9 可知,与查询令牌生成时间开销类似,3 个方案中的密文结果解密时间均为常数,约为0.018 ms。类似的,由于3 个方案都仅需要对单个密文结果进行解密,因此时间开销均为常数。 本文针对云计算环境下的密文图数据最短距离查询外包服务场景,提出一种基于二跳覆盖标记修剪策略的加密图数据精确最短距离外包计算方案。利用广度优先搜索修剪策略对原始标记进行修剪,以减少明文数据长度,提高密文最短距离查询效率。结合安全的密码原语隐藏图数据的结构信息,减少图数据泄露信息,提高方案的安全性。实验结果表明,所提方案在半诚实假设下同时满足随机预言模型下的IND-CPA 安全和(L1,L2)安全,大幅降低了加密时间开销和最短距离查询时间开销。本文方案的时间开销相比文献[22]方案降低了13.04%以上,最短距离查询时间开销相比文献[25]方案降低了36.44%以上。下一步将研究恶意模型下的图数据外包计算及其可验证性问题,即在假设云服务器为恶意状态的前提下,保证返回结果的正确性可验证。4.3 最短距离查询阶段



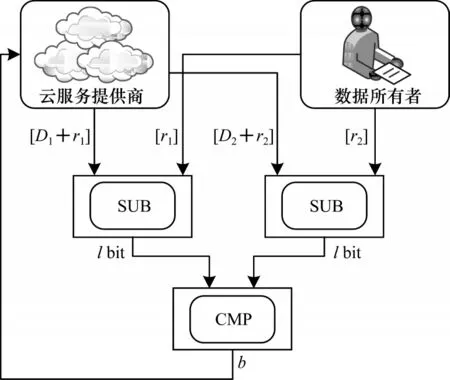
5 安全分析
6 实验结果与分析
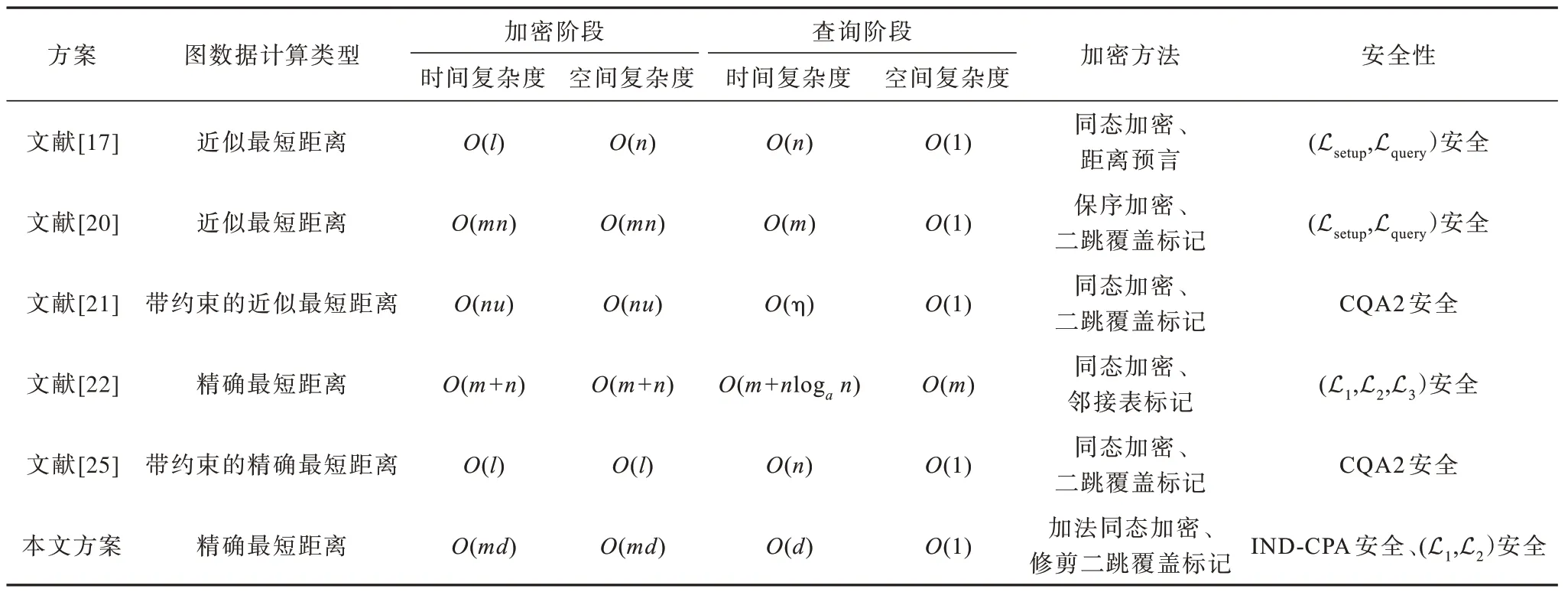
6.1 方案分析与对比
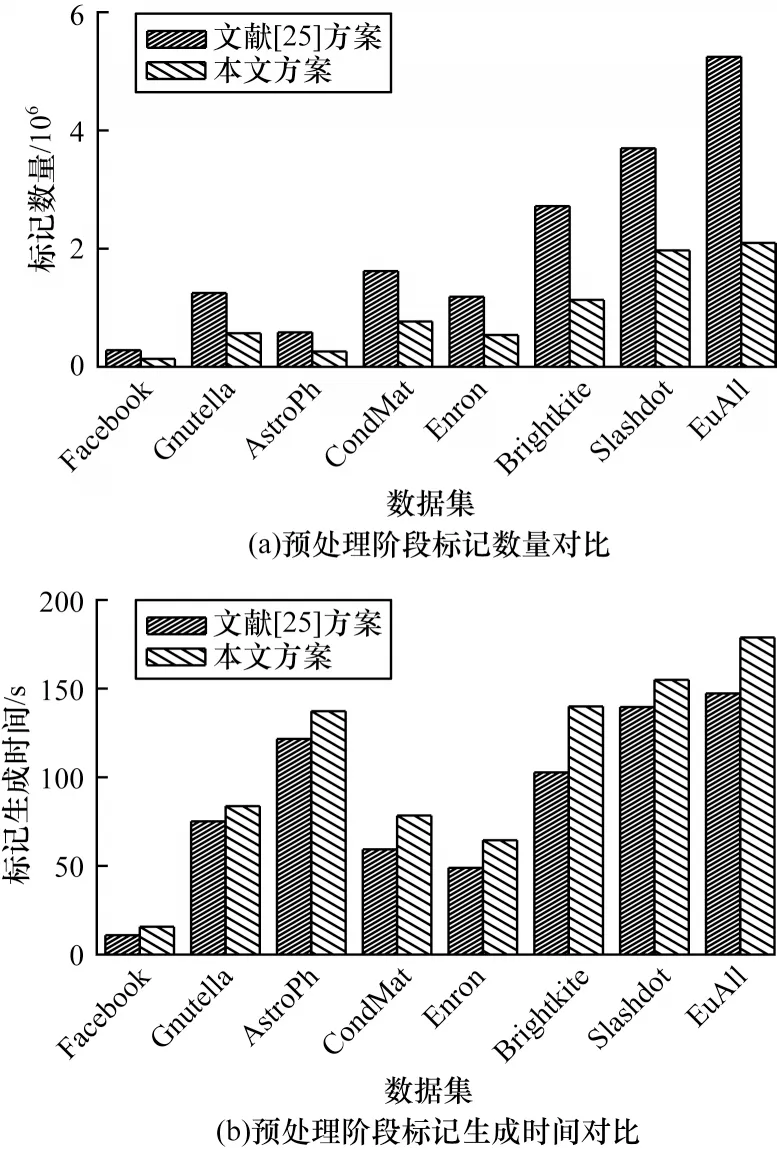
6.2 结果与分析





7 结束语

