基于典型零件加工要素的砂型成形机关键几何误差分析与补偿

李嵩松 马 蔷 侯明鹏 聂应新

（①北京金隅科技学校，北京 102403；②北京机科国创轻量化科学研究院有限公司，北京 100015；③北京工研精机股份有限公司，北京 101312）

随着市场全球化以及竞争的不断加剧，在汽车、机械以及其他重点领域，金属件产品的更新换代速度不断加快，生产周期短、批量小、更新快成为制造业的必然趋势。单件、小批量金属件的快速铸造技术，具有广泛的市场需求。在铸造过程中，要求提高金属件的铸造准确性。砂型成形机主要应用于铸造砂型零件的加工成形，其加工精度决定了砂型零件的尺寸精度进而影响了铸造的准确性。提高砂型成形机的运动系统精度是提高砂型零件加工质量的必要途径[1]。

零件的加工精度主要由加工设备的运动精度决定。根据数控设备的误差来源，影响设备加工精度的主要误差为设备几何误差、热变形误差和切削力误差。Ramesh R 等[2]对设备的误差来源做出了较为详细的论述。其中热变形误差和切削力等误差可以通过改进设备部件等技术手段实现补偿，但是设备制造过程中产生的几何误差是造成零件加工不准确性的主要因素。

几何误差是机械设备制造过程中产生的不可避免的偏差，虽然无法避免，但可以通过研究其特性，并通过数控系统进行必要的补偿，来提高机械设备的加工精度。机械加工设备几何误差动力学建模领域，国内外学者提出了齐次坐标变换矩阵[3-5]，螺旋理论[6-7]，指数模型[8]等方法进行建模。在关键几何误差识别方面：LEE R 等[9]以零件成形理论为思路，在设备制造误差中对设备空间几何误差的影响因子展开了研究。范晋伟等[10]提出了一种用于识别关键几何误差的误差灵敏度分析方法。基于以上研究作为砂型成形机的几何误差为21 项[11]，如果补偿全部几何误差，检测计算补偿的工作量是巨大的，因此识别并补偿关键几何误差的实际意义较大。

针对上述问题，本文提出一种基于典型零件加工要素的砂型成形机几何误差分析与补偿的研究思路，将典型零件加工按设备加工特性，分解为斜四方台、菱形台、圆锥台和圆柱台等4 个典型零件加工要素[12]。然后根据多序体动力学理论建立砂型成形机的体积误差模型。基于实际检测得出设备全部几何误差数据，采用Kim K 等[13]提供的三次多项式拟合方法建立砂型成形机的几何误差模型。同时结合4 种典型零件加工要素的刀具运动轨迹，分别进行关键几何误差分析，并进行相应地补偿，进而提高零件加工精度。

1 误差模型的建立

1.1 成形机的描述与拓扑结构

砂型成形机的结构示意图，如图1 所示，该成形机为高架横梁移动龙门结构，包含X/Y/Z这3 个平动轴，其中X轴包含X0/X1 两个运动轴。其中X轴、Y轴、Z轴均属于刀具运动链。

图1 砂型成形机结构示意图

该成形机的运动链有两个分支，分别为床身到工件的分支（MCS→WCS）和床身到刀具的（MCS→XCS→YCS→ZCS→SCS→TCS），如图2 所示。其中，WCS 为工件坐标系，XCS、YCS、ZCS 为X轴、Y轴、Z轴的坐标系，MCS 为机床坐标系，SCS 为主轴坐标系，TCS 为刀具坐标系。

图2 砂型成形机传递链的拓扑结构

由多体系统理论和拓扑结构分析可以得出此类成形机的各阶低序体阵列，见表1。

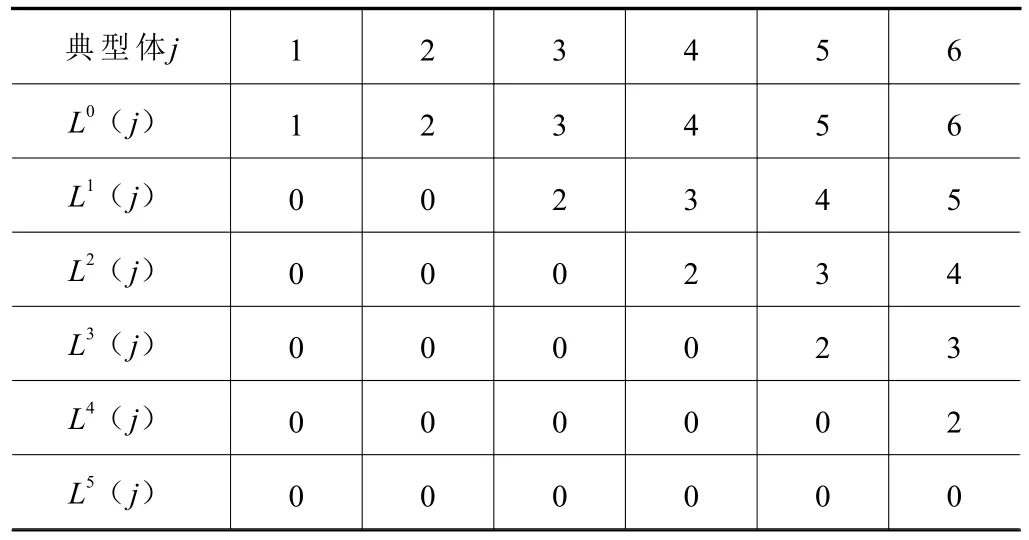
表1 砂型成形机的低序体阵列

1.2 成形机特征矩阵的建立

三轴成形机单轴进给时，在6 个方向存在的微小偏差即为六自由度几何误差。因此，在成形机运动链中，3 个运动部件——X、Y、Z轴，共有18项与位置有关的几何误差（PDGEs），3 项与位置无关的垂直度误差（PIGEs），三轴成形机共有21项几何误差，见表2。表中δ表示线性误差、ε表示角度误差，S表示垂直度误差。

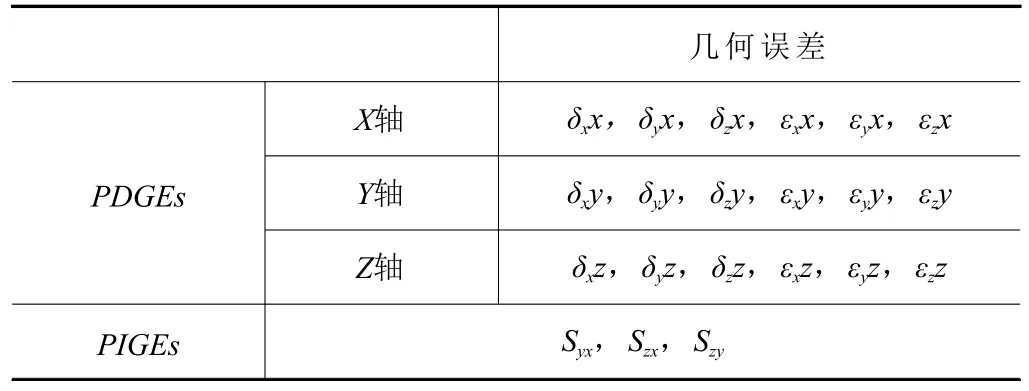
表2 砂型成形机的几何误差列表

综合成形机各个运动部件的运动误差特征矩阵、部件间运动误差特征矩阵、刀具与工件的静止误差特征矩阵等产生成形机各个运动部件特征矩阵。其中由于在实际状态下，刀具与主轴之间无相对运动；工件与工作台无相对运动，因此特征矩阵可以视为单位矩阵。此外，主轴相对于Z轴铣头只有回转运动，且对回转角无定位要求，因此在常规工况下，同样可视为单位矩阵，篇幅所限，以上单位矩阵不在特征矩阵中列出。

在成形机实际的运动过程中，刀尖点的加工轨迹误差是各运动误差项积累和传递的结果，相对于工件的空间位置存在偏差，根据上文中特征矩阵可以进行坐标变换，从而得出刀尖点的空间位置误差ΔE，可由式（12）计算得到。

式中：ΔE为理想点与实际点之间的误差；Pt为实际加工点在机床坐标系中的齐次坐标；PW为理想加工点在工件坐标系中的齐次坐标。

1.3 成形机几何误差模型的建立

本文使用Renishaw 公司的XL-80 激光干涉仪[14-15]和电子水平仪（精度0.001 mm/m）测量成形机X/Y/Z平动轴的全部几何误差，拟合为空间位置的三次多项式函数。关于成形机X轴的6 项几何误差模型的表达式如式（13）所示。

X/Y/Z轴相应的几何误差如下。

式中：x表示成形机X轴的绝对运动量，单位为mm；PDGEs几何误差中。线性误差δxx、δyx、δzx的单位为mm，角度误差εxx、εyx、εzx的单位为rad。

Y轴：

2 零件加工要素下的机床关键几何误差分析

2.1 复杂零件的形状误差建模

包含典型零件加工要素的工件的三维模型，工件由4 部分组成，包括斜四方台，菱形台，圆锥台和圆柱台。其中圆柱台直径为130 mm，高为30 mm；圆锥台，底面直径为218 mm，圆锥角为120°；正菱形台边长为218 mm 高为30 mm；斜四方台斜边夹角为3°；直边长为320 mm；高为20 mm；具有典型零件加工要素的零件模型如图3 所示。包含典型零件加工要素的砂型件的形状误差建模是形状误差分析的前提和基础。如图4 所示，分析过程第一步为对这一复杂砂型件的三维模型进行零件加工要素分解，得到斜四方台，菱形台，圆锥台，圆柱台4 个典型零件加工要素。第一步分解完成后，第二步为基于UG 软件设计完成的刀具走刀路径；第三步为使用UG 软件的后处理功能分别得到砂型成形机加工不同零件加工要素的NC 代码；第四步为将机床各个平动轴的理想运动量代入式（13）～（15）的几何误差模型中，可以得到刀具运动路径中各个位置点的几何误差的值。第五步为得到误差值后，将这些典型零件加工要素的误差值继续代入式（12）的体积误差模型中，最终得到其形状误差模型。

图3 复杂工件的三维模型

图4 典型零件加工要素分布

2.2 零件加工要素下的灵敏度分析

本文提出的根据典型零件加工要素误差识别砂型成形机关键几何误差分析与补偿的方法，利用此方法分析并识别砂型成形机的关键几何误差，结合测量数据和精度检验标准，对砂型成形机进行有针对性地调整和补偿，进而提高砂型成形机的零件加工精度。测量并计算灵敏度影响因子是设备灵敏度分析的先决条件，灵敏度影响因子的精确度是灵敏度分析结果的根本所在，起到决定性作用。

在实际加工中，由误差元素产生的零件加工误差的大小不仅与该误差的灵敏度影响因子有关，也与该误差元素自身大小有关，一个设备几何误差的灵敏度影响因子数值越大，说明该项几何误差对加工零件形状误差的贡献值越高。因此灵敏度影响因子的确定，在灵敏度分析中起着至关重要的作用。如式（16）所示[16]，各几何误差在不同零件加工要素的灵敏度影响因子可定义为

式中：Sn表示设备几何误差n（n=1,2,3,···,21）在不同零件加工要素中的灵敏度影响因子；[Db，Da]表示加工不同零件加工要素的切削运动的运动轨迹长度；En表示仅考虑单一几何误差n得到的轮廓误差曲线；dx表示对切削刀具路径上形状误差的微分。

通过式（16）能得到由单一项几何误差n引起的加工件的形状误差En，可由式（17）分解为3 个方向的分量。

式中：Enx/Eny/Enz分别表示几何误差n在X/Y/Z方向上的误差分量。

误差灵敏度的物理意义为21 项几何误差的单位变化量引起空间位置误差的变化量，单项误差的灵敏度系数越大，说明对设备的空间定位精度误差的贡献越大。为了评估各个单项误差对空间定位误差的相对影响，将各方向的误差灵敏度影响因子进行归一化处理，定义归一化灵敏度影响因子Un，如式（18）所示。

2.2.1 圆锥台要素的灵敏度分析

本文以典型零件加工要素圆锥台为例，论述灵敏度分析过程。将典型加工件的模型输入NX12.0 软件中进行加工编程，NX12.0 生成的刀具轨迹需要经过后处理将刀具轨迹转化为NC 程序代码，通过代码得到机床X/Y/Z的理想运动量。圆锥台刀具轨迹如图5 所示及X/Y/Z轴的理想运动量如图6～8 所示。

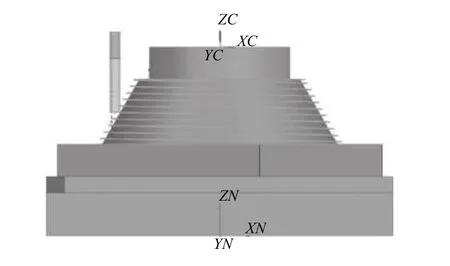
图5 圆锥台刀具加工轨迹

图6 切削圆锥台X 轴理想运动量

图7 切削圆锥台Y 轴理想运动量

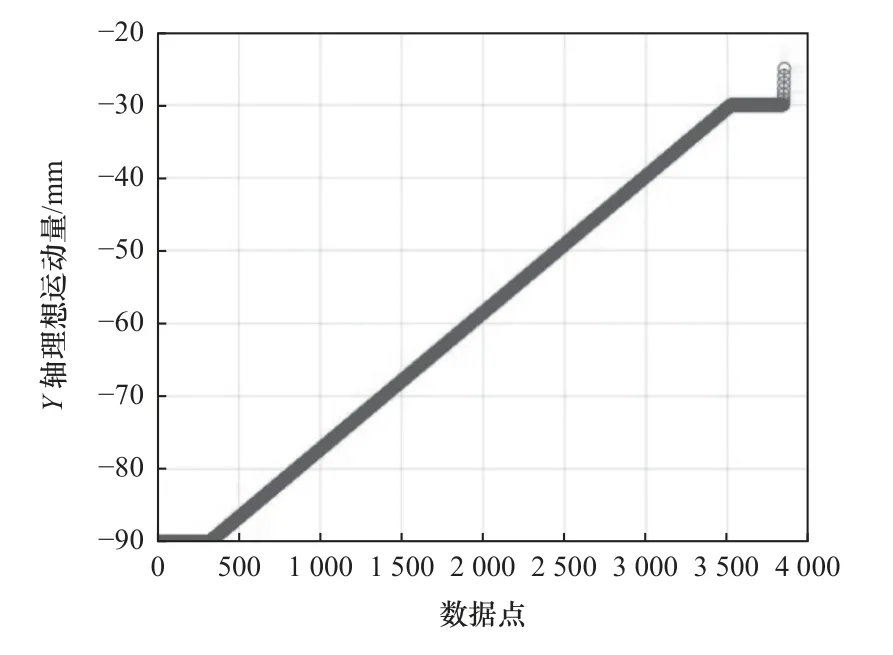
图8 切削圆锥台Z 轴理想运动量

把设备加工圆锥台时X/Y/Z的理想运动量代入式（13）中的设备几何误差模型中，能得出设备在加工圆锥台时各个位置的几何误差值。再将圆锥台的几何误差值代入到设备的体积误差模型中，得到圆锥台的形状误差。

由式（13）～（17），可以得出设备单项几何误差，在典型零件加工要素的归一化灵敏度影响因子。按此方法，可以得出18 项几何误差在圆锥台加工要素的灵敏度分析结果，如图9 所示，从图中可以看出，几何误差εxx、δyz、δzz、δxz引起圆锥台的形状误差的贡献值较大，这4 项几何误差的归一化灵敏度影响因子之和为0.831 6。其中，单项几何误差εxx的归一化灵敏度影响因子为0.457 3，其对设备加工过程中定位误差的贡献值比其他项几何误差对定位误差的贡献值大很多，因此在后续的补偿过程中，对单项几何误差的补偿需要重点研究。

图9 圆锥台加工要素的灵敏度因子分析结果

2.2.2 圆柱要素的灵敏度分析

按上节所述灵敏度分析方法，可得到各项几何误差在圆柱加工要素中的归一化灵敏度影响因子，分析结果，如图10 所示。从图中可以得出，δyy、δxy、δzx这3 个单项几何误差的归一化灵敏度影响因子之和为0.771 9。其中δyy单项几何误差的归一化灵敏度影响因子为0.501 2，其对设备加工过程中定位误差的贡献值比其他项几何误差对定位误差的贡献值大很多，因此在后续的补偿过程中，对单项几何误差的补偿需要重点研究。

图10 圆柱台加工要素的灵敏度因子分析结果

对比圆锥台和圆柱台两项零件加工要素，将归一化灵敏度影响因子按数值大小进行排位对比，得出结论为灵敏度影响因子排位略有不同，但总体影响趋势基本相同。通过对比圆锥台和圆柱台要素中排位相同的单项几何误差的归一化灵敏度影响因子不尽相同。因此得出根据典型零件加工要素进行灵敏度分析可以对设备几何误差之间的差异进行有效地识别，为后续计算设备的补偿数据提供准确有效的基础数据保障。

本文所涉及的成形机各单项几何误差的归一化灵敏度影响因子大于0.15 的为关键性几何误差，从图8 和图9 可以得出关于涉及圆锥台和圆柱台形状公差的关键几何误差，结果见表3 所示。从表中可以得出，关于圆柱台加工要素的设备关键几何误差共计9 项，此九项均是与位置有关的误差；对于圆锥台特征，共有设备关键几何误差共13 项，均是与位置有关的误差。因此可认为与位置有关的误差PDGEs对圆柱台和圆锥台的形状误差起着重要的影响作用。

表3 影响圆柱台和圆锥台关键几何误差

2.2.3 斜四方形和菱形要素的灵敏度分析

由于砂型成形机设备加工斜四方形和菱形只需要X/Y两轴联动即可完成加工，所以Z轴相关几何误差无影响。

根据2.2.1 节中求取圆锥台的几何误差灵敏度影响因子的方法，应用该方法求出各项几何误差在斜四方台和菱形台加工要素中的归一化灵敏度影响因子，结果分别如图11、12 所示，对比图9、10可知，斜四方形台和菱形台要素的关键项几何误差较为相似，其中，δzx、δyx、εyy、δyy这4 项的归一化的灵敏度影响因子之和超过70%。斜四方台和菱形台中相同项几何误差的归一化灵敏度影响因子值的大小是不同的，其中关键项几何误差δzx、δyx、εyy、δyy的灵敏度影响因子的数值大小存在差异。

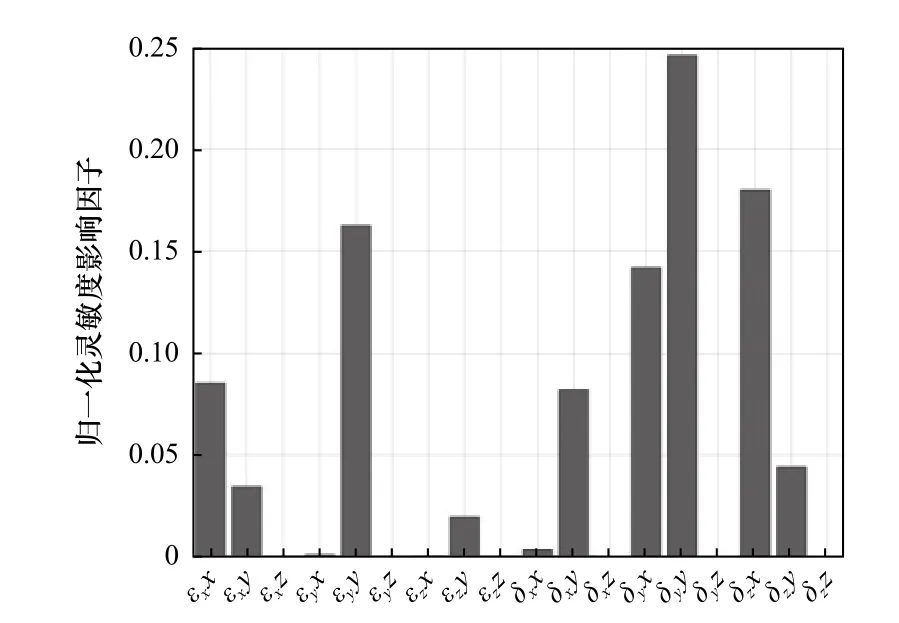
图11 斜四方台加工要素的灵敏度因子分析结果

图12 菱形台加工要素的灵敏度因子分析结果

基于上述分析的基础上，可得到影响斜四方台和菱形台加工要素的关键几何误差，见表4，从表中得出对于斜四方台要素，共有10 项关键几何误差，其中线性误差有6 项，因此得出结论。线性误差是影响斜四方台和菱形台形状误差的重要因素。

表4 影响菱形台和斜四方台的关键几何误差排序

3 典型零件加工要素下的机床关键几何误差补偿试验

根据上文所述分析可得，圆柱台、圆锥台、斜四方台和菱形台这4 个零件加工要素的关键几何误差归一化灵敏度影响因子之和均大于90%，分别为99.82%、99.72%、99.90%和99.93%，将上述的零件加工要素的关键几何误差分别代入到成形机的体积误差模型中计算其在总误差中的占比，结果见表5 所示。

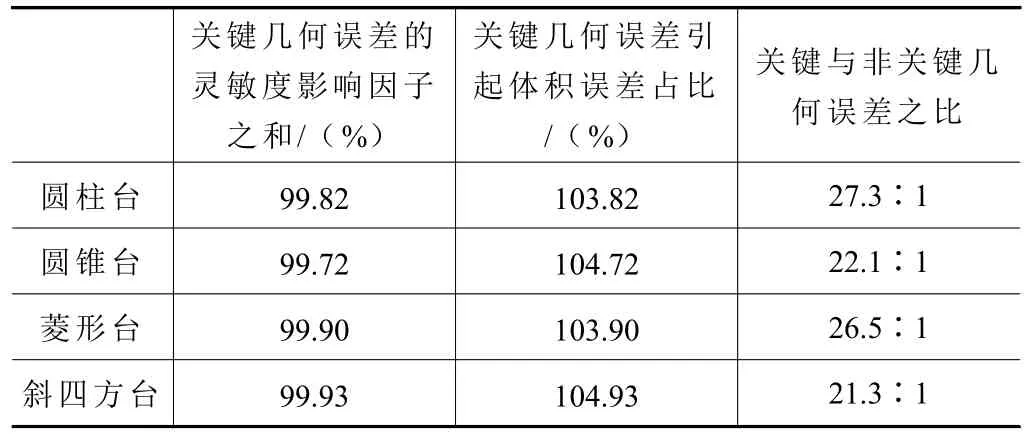
表5 关键几何误差占比分析

关键几何误差引发体积误差占比在特征中均大于1，表明非关键几何误差引发体积误差占比分别为-3.82%、-4.72%、-3.9%和-4.93%，结果表明关键几何误差与非关键几何误差对体积误差中的作用效果相反，对比结果，可知关键几何误差占比大于非关键几何误差，因此，关键几何误差对体积误差的影响具有决定性作用，进而证明本文中的检测试验方法的正确性。

通过本文中提出的基于典型零件加工要素的几何误差补偿方法，其优点在于通过典型加工要素的检验指标能够与运动轴公差形成映射关系，通过映射关系，使砂型机的精度补偿与检验标准以及典型零件公差之间建立多元耦合映射关系，实现砂型机加工精度目标的优化分配。使得优化工作有的放矢地执行，传统数控机床在实际生产中一般只进行定位补偿。砂型机根据这一方法能够通过切削零件，检测零件精度，对砂型机进行诊断和全面的补偿。

本文在一台CAMTC-SMM2000 型砂型成形机上进行切削与补偿的试验，SMM2000 型砂型成形机的机械参数为X轴行程2 000 mm，Y轴行程2 000 mm，Z轴行程800 mm，各轴进给速度为5 000 mm/min，将圆锥台、圆柱台、斜四方台和菱形台这4 个加工要素的关键几何误差分别代入式（12）的设备体积误差模型中，按参考文献中的方法，按照逆运动学方法，计算补偿后X/Y/Z轴的运动值，从而得到补偿后的设备代码[17]。应用补偿程序后设备加工出的砂型零件。如图13 所示。

图13 补偿后加工的砂型件

按照砂型件精度检验标准的检测项目分布，如图14 所示。应用手持非接触式检测仪对复杂砂型零件进行扫描并检测零件误差，如图15 所示。补偿后的4 个典型零件加工要素误差平均值和补偿率，见表6。补偿后4 个典型零件加工要素的平均误差分别为38.1 μm、20.2 μm、41.2 μm 和31.3 μm，加工精度提高55%～70%，其中误差平均值为：将零件各项误差值按灵敏度影响因子进行加权得出各个特征的误差平均值，例如圆柱台加工要素中圆度和高度的精度提高值按相关误差项的影响因子加权平均得出误差平均值。通过误差平均值的提高可以得出本文补偿方法对于砂型成形机加工精度的提高是有效的。

表6 补偿前后的典型加工要素误差平均值及补偿率

图14 手持非接触式检测仪

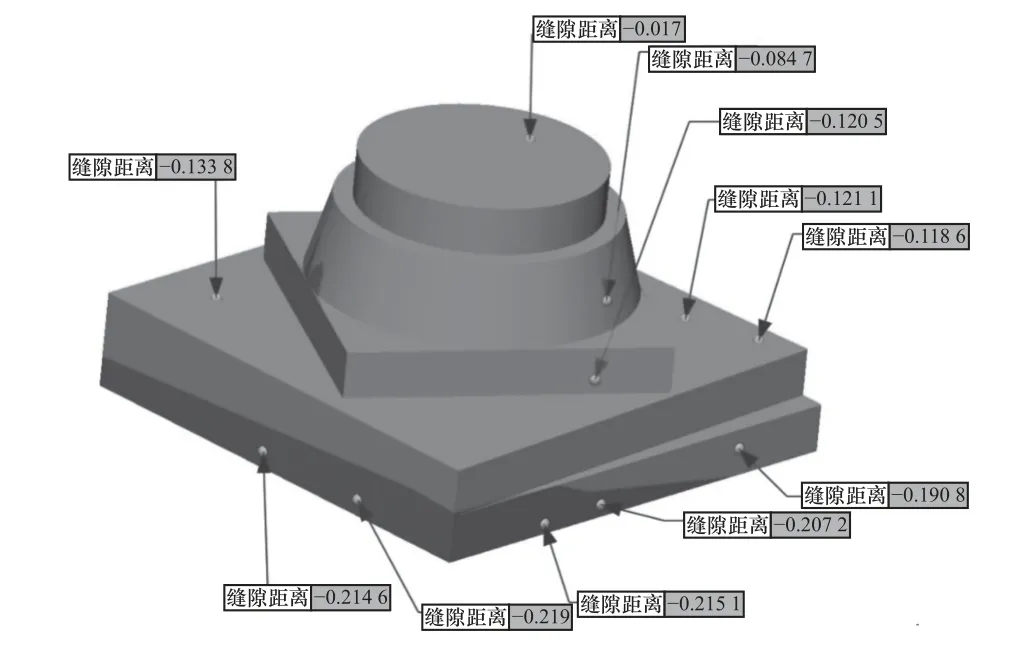
图15 零件检测项目分布图

4 结语

本文从典型零件加工要素出发，通过研究加工零件要素的形状误差与设备体积误差之间的关系，提出一种基于典型零件加工要素的数控设备几何误差辨识与补偿的研究思路。通过对圆柱台、圆锥台、菱形台、斜四方台这4 种典型零件加工要素的灵敏度影响因子的分析与补偿，初步检验了这一研究思路的可行性和有效性，得出了结论如下：

（1）影响典型零件加工要素形状误差的关键几何误差项虽然有相似之处，但对于同一单项几何误差的归一化灵敏度影响因子在不同加工要素中的大小并不相同。因此在补偿时需要进行区分。

（2）在分析各个典型零件加工要素的关键几何误差中，线性误差占比很大，因此得出各项线性误差对各个典型零件加工要素形状误差起决定性作用。

（3）对于各项关键几何误差，由归一化系数的分布可以得出。

（4）基于CAMTC-SMM2000 成形机的误差补偿试验结果显示，补偿后的典型零件加工要素的加工精度提高了55%～70%，因此本文提出的基于典型零件加工要素的灵敏度分析与补偿的方法是有效的。