基于最大后验概率准则的天基星座网络多用户检测方法
张克楠,李兴乾,杨胜,丁凯
北京空间飞行器总体设计部,北京 100094
1 引言
天基星座网包含地球同步轨道卫星,中轨道卫星和低轨道卫星,是一种自组织无中心节点的无线网络,网络中的用户随意进出自由组网。由于天基星座网的特殊性导致其网络拓扑动态变化[1-3],网络中活动用户的数量、身份和传输数据随时间而变化,多用户检测能够识别和检测出每个活动用户的身份和传输的数据,对于消除多址干扰、提高网络容量具有重要作用[4-8]。
在过去的几十年里,研究人员提出了各种多用户检测方法。然而许多方法[9-12]都是基于活动用户的数量是已知的并且等于网络可以容纳的最大用户数这一假设。这个假设通常过于粗略,基于这个假设进行多用户检测会导致严重的性能下降。因为许多用户可能处于非活动状态,因此每个时刻的活动用户数都是不同且未知的。文献[13]和文献[14]分别提出了一种两级解码器,由活动用户识别器和多用户检测器组成。由于作者没有为用户活动状态建立任何模型,因此该方法只能应用于静态环境。文献[15]提出一种逐幸存者处理算法和两种基于粒子滤波的算法。尽管这三种算法的适用范围很广,但其误码率性能并不理想。本文提出一种基于最大后验概率准则的多用户检测方法,该方法将用户的活动状态建模为马尔科夫链,利用用户活动状态模型构建网格图,将多用户检测转化为在网格图中使用BCJR算法搜索最优路径,利用最优路径估算活动用户的数量、身份和传输数据。仿真结果表明与文献[15]提出的3种方法相比,本文所提方法在活动状态错误概率和符号错误概率两个指标均取得了更好的性能。
2 基于最大后验概率准则的多用户检测方法
2.1 活动状态建模
假设一个有Q个用户的天基星座网络,网络中每个用户都可以自由地进出并通过加性高斯白噪声信道同步传输数据。给每个用户分配一个长度为M的扩频码。对于第k个符号间隔,接收信号yk(t)可以表示为
yk(t)=xk(t)+n(t),t∈[0,T]
(1)
式中:T表示符号间隔;n(t)是加性高斯白噪声;xk(t)是活动用户发送信号的叠加,其中活动用户的数量未知,xk(t)可以表示为
(2)
式中:bq(k)是用户q在第k个符号间隔发送的符号。如果用户q处于活动状态,则bq(k)为独立同分布随机变量,服从伯努利分布,并以相等的概率取值“+1”或“-1”,“+1”表示二进制符号“0”;“-1”表示二进制符号“1”。如果用户q处于非活动状态,则bq(k)为0。cq(t)表示用户q的扩频码波形。它可以表示为
(3)
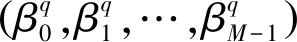
将(2)代入(1)中可得
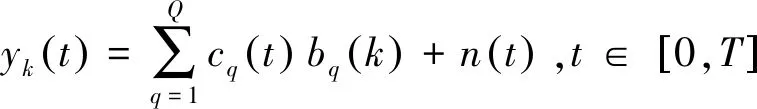
(4)
接收用户对yk(t)进行码片匹配滤波和码片速率采样,将yk(t)转化为矢量形式yk,如式(5)所示。
yk=xk+nk=

(5)
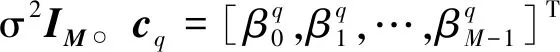
yk=xk+nk=
CBk+nk
(6)
式中:C=[c1,c2,…,cQ]是由网络中Q个用户的扩频码组成的扩频码矩阵;Bk=[b1(k),…,bQ(k)]T是由±1和0构成的Q维向量,表示在第k个符号间隔Q个用户的发送符号。
定义随机变量uq(k)表示用户q在第k个符号间隔的状态,即
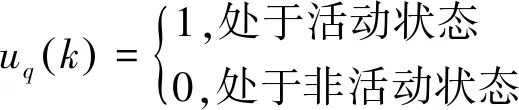
(7)
uq(k)由用户q在第k个符号间隔发送的符号bq(k)决定,即
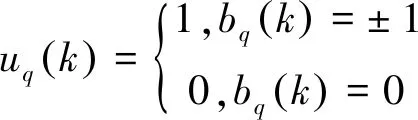
(8)
可以通过式(9)建立用户活动状态的动态模型:
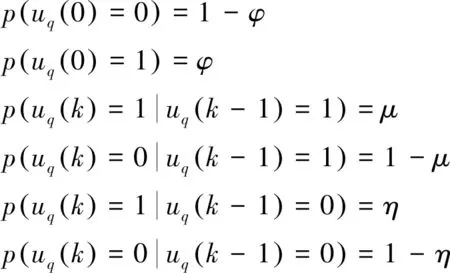
(9)
式中:φ是用户在开始时刻处于活动状态的先验概率;μ是用户在第k-1个符号间隔处于活动状态的条件下,在第k个符号间隔也处于活动状态的概率;η是用户在第k-1个符号间隔处于非活动状态的条件下,在第k个符号间隔处于活动状态的概率;式(9)所描述的模型表明,对于固定的用户q,uq(k)是一个马尔科夫链。由于uq(k)被建模为马尔科夫链,bq(k)也可以被建模为马尔科夫链,如式(10)所示。
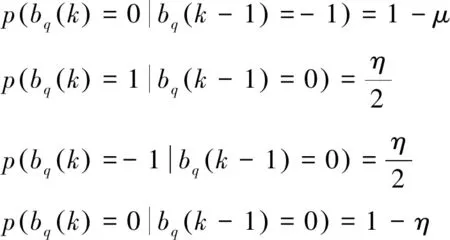
(10)
2.2 网格图构建
假设数据包长为K个符号,Q个用户的发送符号矩阵B如式(11)所示。

(11)
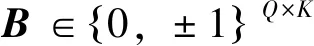
CB
(12)
式中:X∈RM×K,相应的接收信号矩阵Y如式(13)所示。
Y=X+N=CB+N
(13)
式中:Y∈RM×K,N∈RM×K。
本文提出的方法将多用户检测转换为在图1所示的网格图中搜索最优路径,计算每个用户在每个符号间隔发送符号的对数后验概率如式(14)所示。通过比较式(14)中3个对数后验概率得到每个用户在每个符号间隔发送符号的估计值如式(15)所示。
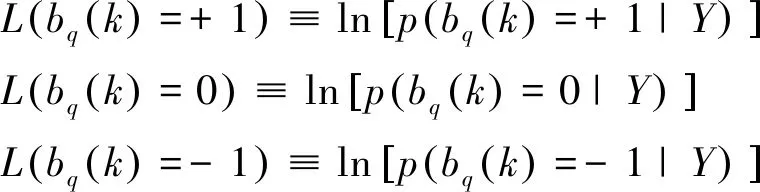
(14)

(15)
网格图由K+1列组成,每列都由F个状态Sj=[sj1,sj2,…,sjQ]T∈{±1,0}Q×1,j=1,…,F组成,每行状态相同,每个状态都是三元Q维向量。除第一列和最后一列以外,每列的每个状态都有F个分支进入和离开。每个分支连接相邻列的两个状态表示一种状态转移。所有离开同一个状态Sj的分支都在分支上标记相同的输入向量ej和相同的输出向量vj,ej等于Sj。第k列和第k+1列之间的ej表示符号向量Bk的一种可能取值,ej的每个元素表示bq(k)的一种可能取值。与ej对应的vj表示xk的一种可能取值。因此可得
vj=Cej,j=1,…,F
(16)
2.3 网格图搜索
本文方法使用BCJR[16]算法对网格图进行搜索计算每个符号间隔每个用户发送符号的对数后验概率。搜索过程从网格图第1列的任意状态开始,至第K+1列的任意状态结束,因此共有3Q(K+1)条不同的路径,每条路径表示发送信号X的一种可能取值。
将后验概率p(bq(k)=+1|Y)表示为式(17)所示。

(17)
式中:∑k+1是与bq(k)=+1对应的所有状态对S′和S的集合,其中S′属于第k列,S属于第k+1列。
将p(bq(k)=0|Y)和p(bq(k)=-1|Y)以相同方式表示,如式(18)和式(19)所示。
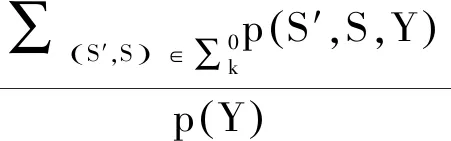
(18)

(19)
式中:∑k0和∑k-1是分别与bq(k)=0和bq(k)=-1对应的所有状态对S′和S的集合,其中S′属于第k列,S属于第k+1列。
由于接收向量Y是一个确定值,因此p(Y)=1。于是式(14)可以表示为式(20)。
L(bq(k)=+1)≡ln [p(bq(k)=+1|Y)]=
L(bq(k)=0)≡ln [p(bq(k)=0|Y)]=
L(bq(k)=-1)≡ln [p(bq(k)=-1|Y)]=
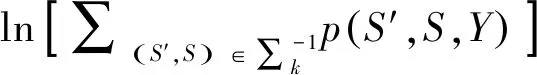
(20)
将p(S′,S,Y)表示为式(21)所示形式:
p(S′,S,Y)=p(S′,S,Yt
(21)
式中:Yt

(22)
式中:最后一个等式是因为第k+1个符号间隔的接收信号仅依赖于网格图第k+1列的状态。定义
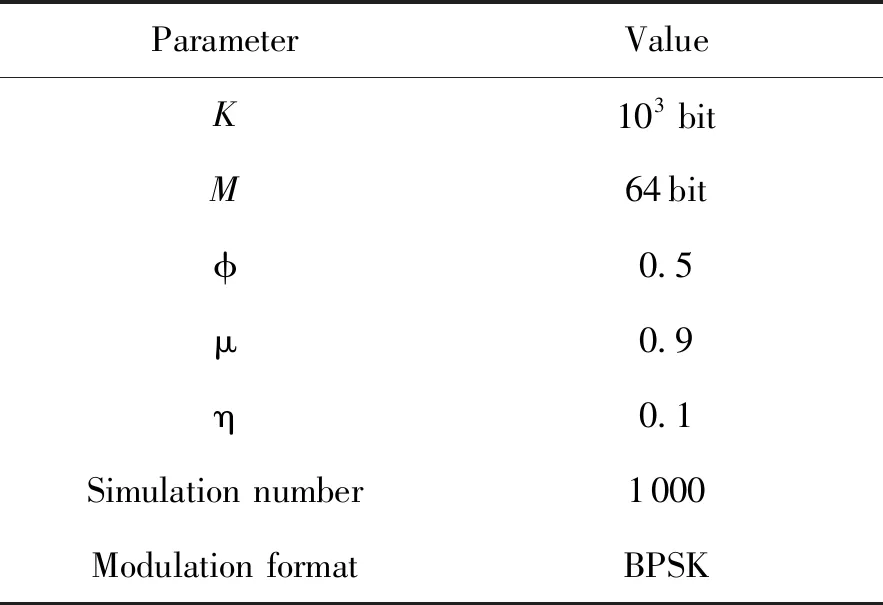
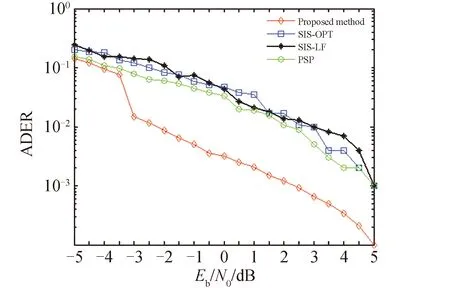
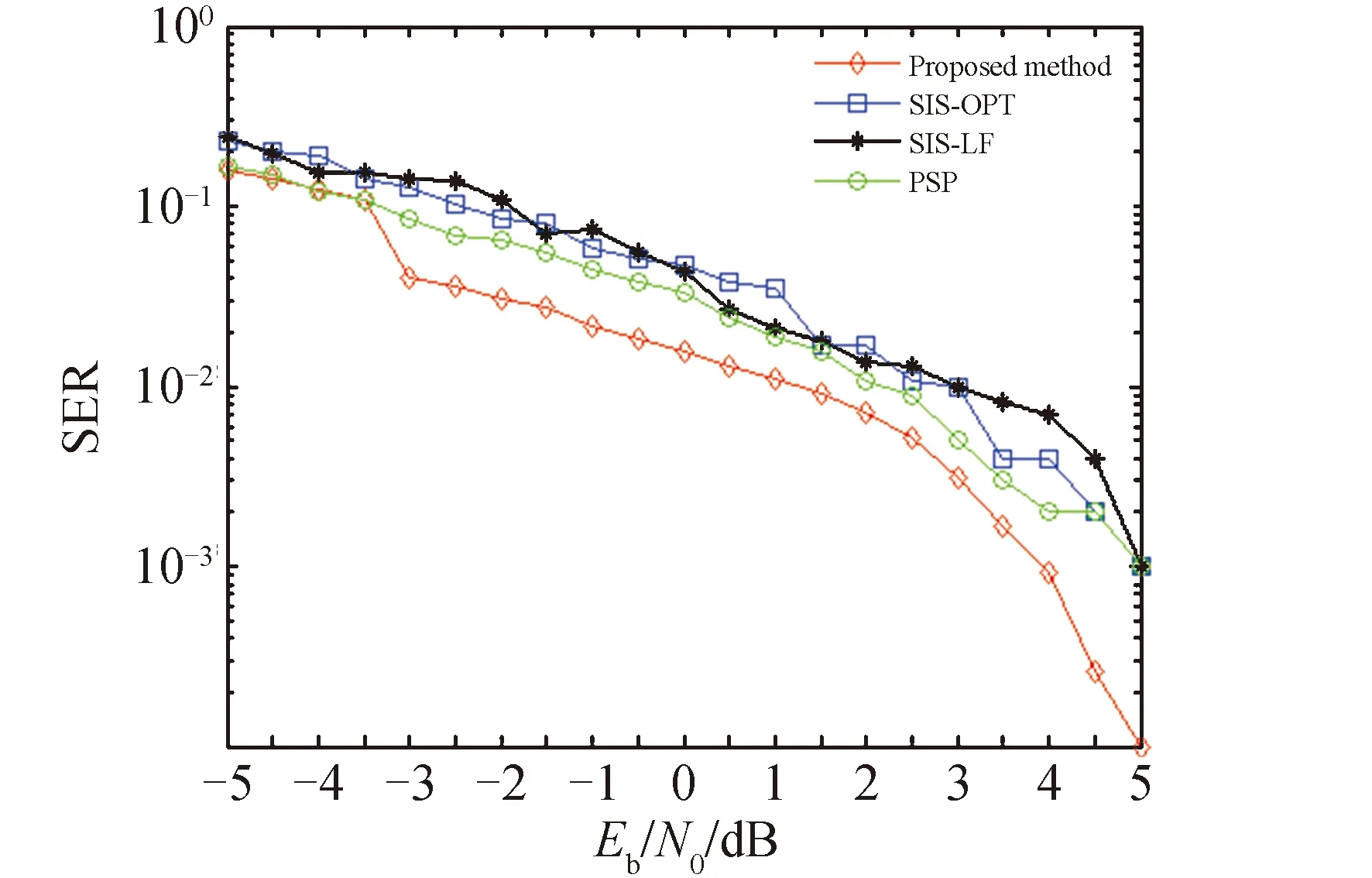
αk(S′)≡p(S′,Yt γk(S′,S)≡p(S,yk|S′) βk+1(S)≡p(Yt>k|S) (23) 分别对αk+1(S)和βk(S′)进行前向递归和后向递归,可得: (24) (25) 式中:δk和δk+1分别为第k列和第k+1列所有状态的集合。前向递归从第1列任意状态开始,后向递归从第K+1列任意状态开始。因此前向递归的初始条件和后向递归的初始条件分别如式(26)和(27)所示。 α1(S)=1/3Q (26) βK+1(S)=1/3Q (27) γk(S′,S)可以表示为: γk(S′,S)=p(yk|S′,S)p(S|S′)= p(yk|e)p(S|S′) (28) 对于噪声方差为σ2的高斯白噪声,有 (29) 由于不同用户发送的符号相互独立,因此p(S|S′)可以被分解为: (30) 式中:Sq′和Sq是bq(k)和bq(k+1)的可能取值。根据式(10)所示,p(Sq|Sq′)有4种可能取值:μ/2,1-μ,η/2,1-η。将式(29)和(30)代入式(28)中可得: (31) 引入对数域表征并利用式(32)和式(33)简化式(24),(25)和(31)的计算,可得式(34)~(38)。 max*(x,y)≡ln (ex+ey)= max (x,y)+ln (1+e-|x-y|) (32) max*(x,y,z)≡ln (ex+ey+ez)= max*(max*(x,y),z) (33) (34) (-Q)ln 3 (35) 1,2,…,K (36) (-Q)ln 3 (37) K,K-1,…,1 (38) 将式(22)和式(20)表示为式(39)和式(40)。 (39) (40) 假设天基星座网络中的用户在高斯白噪声信道上同步传输数据。仿真实验参数如表1所示。将本文方法与文献[15]中的方法“SIS-OPT”、“SIS-LF”和“PSP”从活动状态错误概率(activity detection error rate,ADER)和符号错误概率(symbol error rate,SER)两个指标进行比较。 表1 仿真试验参数 指定网络中的一个用户为参照用户,计算该用户在每个符号间隔的活动状态错误概率和符号错误概率。活动状态错误概率表示参照用户活动状态的估计值与实际值不同的概率,符号错误概率表示参照用户发送符号的估计值与实际值不同的概率。可以看出活动状态检测错误会导致符号检测错误,但反之不成立。 图2展示了4种方法的活动状态错误概率在不同信噪比Eb/N0下的取值。可以看出当Eb/N0=-3dB时,本文方法的活动状态错误概率急剧下降。当Eb/N0>-3dB时,本文方法的性能远优于其他3种方法。与其他3种方法相比,当活动状态错误概率等于10-3时,本文方法可以获得2.6dB 信噪比增益。 图2 ADER性能曲线 图3展示了4种方法的符号错误概率在不同信噪比Eb/N0下的取值。当活动状态错误概率等于10-3时,与其他3种方法相比本文方法可以获得1dB信噪比增益。此外可以看出图3中曲线的走势与图2非常相似。实际上通过仿真实验可以发现大多数符号错误都是由于没有正确检测出参照用户的活动状态造成的。因此保持较低的活动状态错误概率对于获得较低的符号错误概率是非常必要的。 图3 SER性能曲线 本文主要研究天基星座网络中的多用户检测问题。针对传统方法建模比较简单且误码率性能不佳的问题,提出了一种基于最大后验概率准则的多用户检测方法。该方法将用户的活动状态建模为马尔科夫链,利用用户活动状态模型构建网格图,将多用户检测转化为在网格图中使用BCJR算法搜索最优路径,利用最优路径估算活动用户的数量、身份和传输数据。仿真结果表明大多数符号错误是由于没有正确检测出用户的活动状态造成的,因此降低活动状态错误概率至关重要。与对照方法SIS-OPT。SIS-LF和PSP相比,当活动状态错误概率和符号错误概率达到10-3时,本文方法分别获得2.6dB和1dB信噪比增益。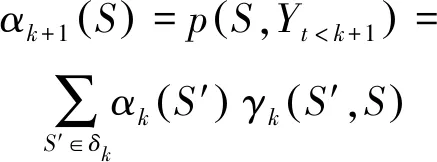
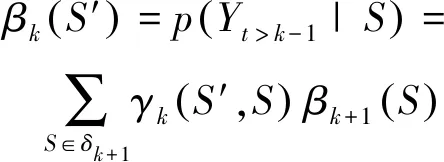
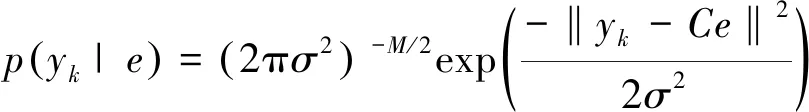
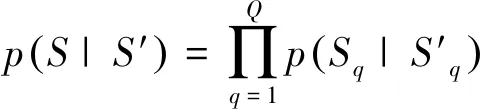
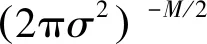
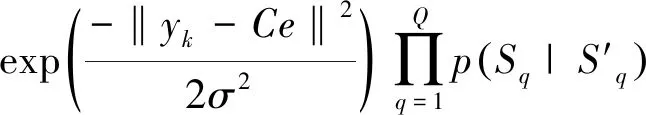
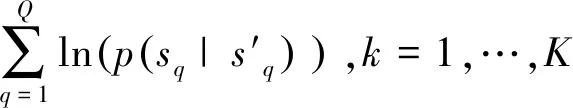
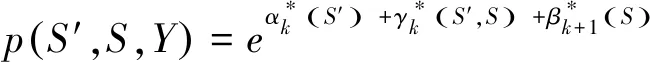
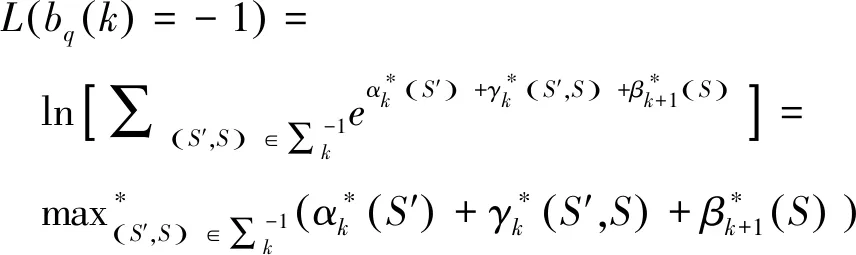
3 仿真分析
3.1 试验场景和参数
3.2 试验结果和分析
4 结论

