基于卡尔曼滤波平滑多普勒值的单频周跳探测方法

武威,刘荟萃,曹建峰,鞠冰,王潜心,吴志远

1.中国矿业大学 环境与测绘学院,徐州 221116

2.北京航天飞行控制中心,北京 100094

1 引言

GNSS单频接收机具有成本小、功耗低的优点[1],因此在高轨卫星上多搭载此类设备辅助测定轨[2]。但是,高轨卫星的单频GNSS数据处理还存在一些难以解决的问题,载波相位数据处理中的周跳探测就是其中之一[3-4]。高轨卫星上搭载的GNSS接收机接收到的信号功率低、失锁频繁,极易导致周跳发生,进而造成定位精度降低;但受到观测值测量精度和采样率等因素的制约,准确的周跳探测较难实现。

目前已有的单频周跳探测方法主要有高次差法[5]、多项式拟合法[6-7]、伪距相位组合法[8]、Kalman滤波法[9-10]、多普勒法[11-13]。这几种方法各有其特点和局限性。高次差法简单易用,但是在放大周跳的同时会放大噪声。多项式拟合法需要保证拟合窗口内没有发生周跳,才能使用拟合结果准确探测周跳。伪距相位组合法受伪距精度影响较大,而单频接收机接收到的伪距观测值观测精度一般较低。Kalman滤波法先验观测噪声及过程噪声的精度依赖于工程经验,需要适当的设置以保证滤波效果。传统的多普勒法引入多普勒观测值,并对多普勒值进行积分,以积分值与前后历元载波观测值的变化的差作为周跳检验值,该方法受卫星高度角变化的影响小,但是会受到多普勒观测值精度和采样间隔的影响。

针对高轨卫星GNSS数据测量精度较低的现实难题,本文提出了基于卡尔曼滤波平滑多普勒值的周跳探测方法,以下进行深入阐述分析。

2 多普勒法周跳探测

2.1 传统多普勒法周跳探测的原理

载波相位和多普勒观测方程表示为[14]:

φ(t)=ρ(t)+c(dt(t)-dT(t))-I(t)+

λ·N(t)+T(t)+εφ(t)

(1)

(2)

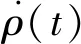
在t-1和t两个相邻历元,对式(2)求均值,对式(1)做差:

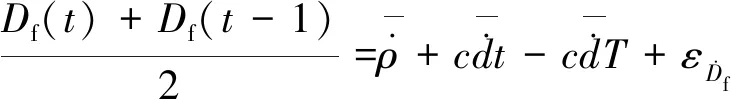
(3)

φ(t)-φ(t-1)=

Δρ+cΔdt-cΔdT+λ·ΔN+εφ

(4)

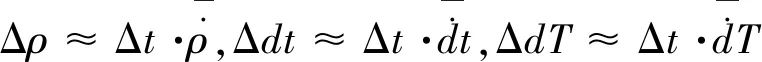
(5)

则式(3)可表示为:

(6)

再对式(6)和式(4)做差,消去其中的接收机钟差cΔdt、卫星钟差cΔdT,可得:

γ(t)≡φ(t)-φ(t-1)-

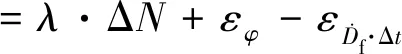
(7)

上式γ(t)为周跳检测量,可以看出其周跳检出效果主要受载波相位观测值和多普勒观测值测量误差影响。

2.2 基于卡尔曼滤波平滑多普勒值周跳探测的原理

在高轨应用背景下,星载GNSS接收机的多普勒观测精度一般较差,导致多普勒法难以探测周跳,为解决这一问题,本文提出了基于卡尔曼滤波平滑多普勒值的周跳探测方法。

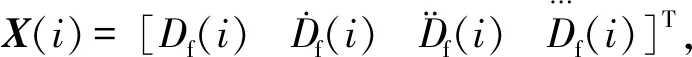
X(i)=AX(i-1)+Ψq(i-1)

(8)

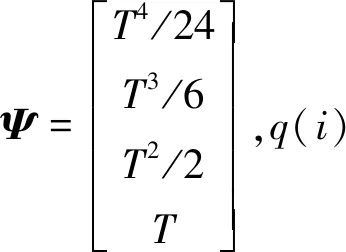
将t时刻的多普勒观测值记为Df(i),则观测方程可表示为:

Df(i)=BX(i)+v(i)

(9)

式中:B=[1 0 0 0],v(i)为测量误差,其方差为σ2。

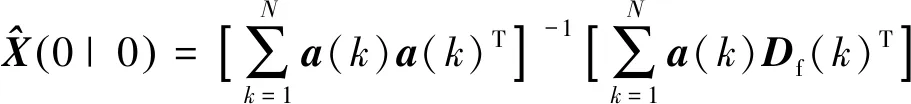
(10)

式中:a(k)=[1 (k-N)T(k-N)2T2/2 (k-N)3T3/6]T,则第k个历元的多普勒观测值Df(i)方差计算公式为:

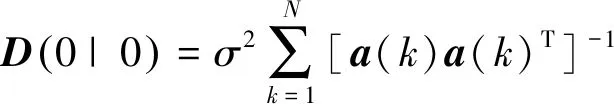
(11)

因此,Kalman滤波递推公式过程如下[15]:

(12)

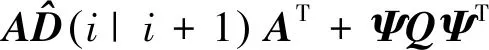
(13)

(14)

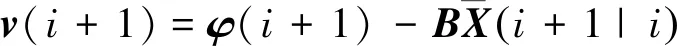
(15)

(16)

D(i+1|i+1)=

[I-J(i+1)B]D(i+1|i)

(17)

式中:Q表示状态噪声协方差矩阵,Q=E[q(i)2],Q的大小反映了状态转移模型的“逼真”程度[16]。当三阶多项式模型能较好地模拟系统状态转移时,Q的元素可以取较小的值。

使用平滑后的多普勒值和载波相位观测值根据式(7)计算得到传统周跳探测量γKalman(t)。由于卡尔曼滤波平滑多普勒值时易受周跳和粗差影响导致系统性误差,此时得到的传统周跳探测量γKalman(t)对于小周跳的探测能力不强,因此使用相同的方法再次计算t+1时刻的传统周跳探测量γKalman(t+1),在得到两个相邻时刻的传统周跳探测量γKalman(t)和γKalman(t+1)后,对两值做差得到最终的周跳探测量Δγ(t,t+1),通过一阶差分,可以在减少系统误差的同时突显周跳。对Δγ(t,t+1)设置适当阈值δ,即可判定是否发生周跳。

3 试验与分析

采用2014年11月1日的探月三期再入返回试验任务中月地转移段返回舱接收到的GPS观测数据对上述算法进行验证分析,该段数据的基本情况如表1所示。本文对原始观测数据与添加仿真周跳的观测数据,分别使用传统的多普勒法和基于卡尔曼滤波平滑多普勒值的周跳探测方法进行周跳探测,对两种方法的结果进行比较,验证基于卡尔曼滤波平滑多普勒值的周跳探测法相对于传统多普勒周跳探测法的优越性。

表1 观测数据基本情况

3.1 两种方法对无周跳数据处理比较

试验1分别使用传统的多普勒法和基于卡尔曼滤波平滑多普勒值的周跳探测方法对实验数据的噪声水平进行检验,不同方法计算得到的残差大小可以反映该方法对观测噪声的敏感程度[10]。从图1可知,传统的多普勒法最大值到了6.3周,标准差为2.209,对小周跳的检测能力较弱。从图2可知,基于卡尔曼滤波平滑多普勒值的周跳探测法周跳探测量最大值为1.2周,标准差为0.3047,在低信噪比条件具有更好的检测能力。

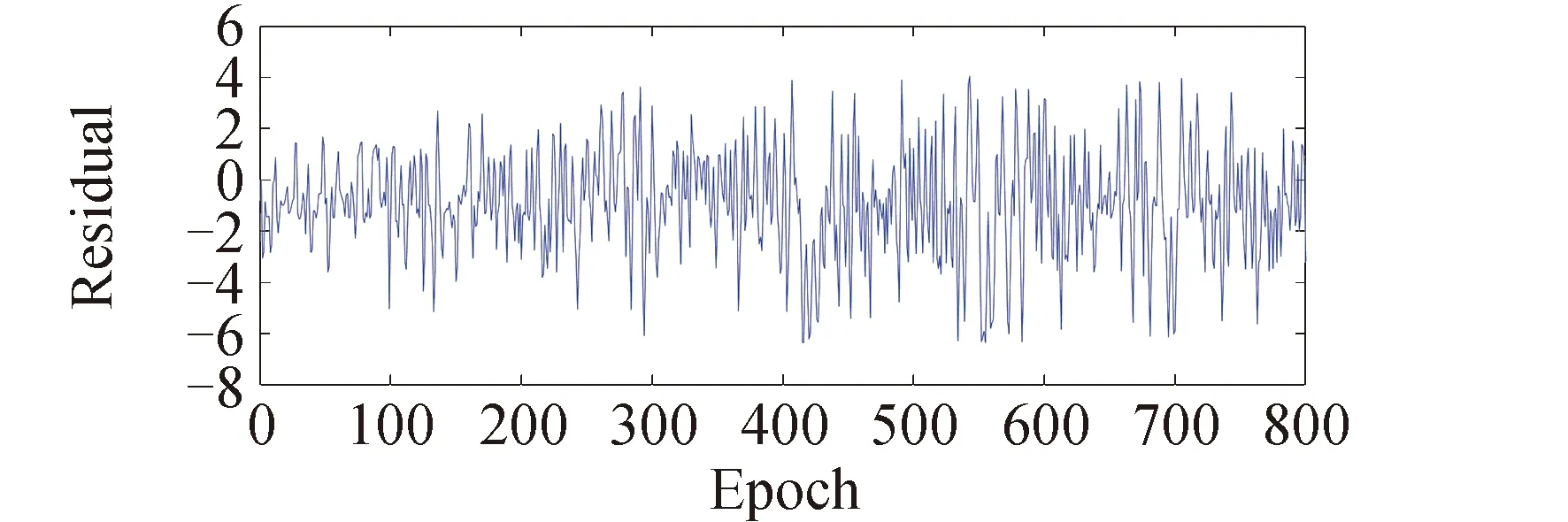
图1 无周跳情况传统多普勒周跳探测法周跳探测结果

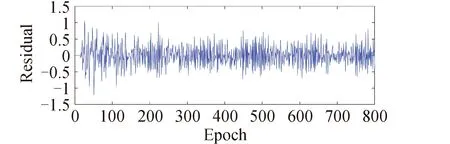
图2 无周跳情况改善的周跳探测法周跳探测结果

状态方程模型误差q(i)对于滤波算法的收敛特性影响较大。图3中是实测数据周跳探测量的标准差随q(i)的变化趋势,其中横坐标表示lg(q(i))。可以看出,如果q(i)小于10-8后继续减小,滤波效果的提升已经不明显,因此本文取q(i)=10-8。

图3 周跳探测量的标准差随q(i)的变化

3.2 两种方法周跳探测能力的比较

对全部实测数据发生中的周跳进行了统计分析,结果显示如图4所示,探测出的周跳达90次,其中小于6周的周跳发生了25次以上。由于小周跳发生较多且难以探测,为更好地检验算法性能边界,本文又在6个历元处添加了小周跳,其位置和大小如表2所示。

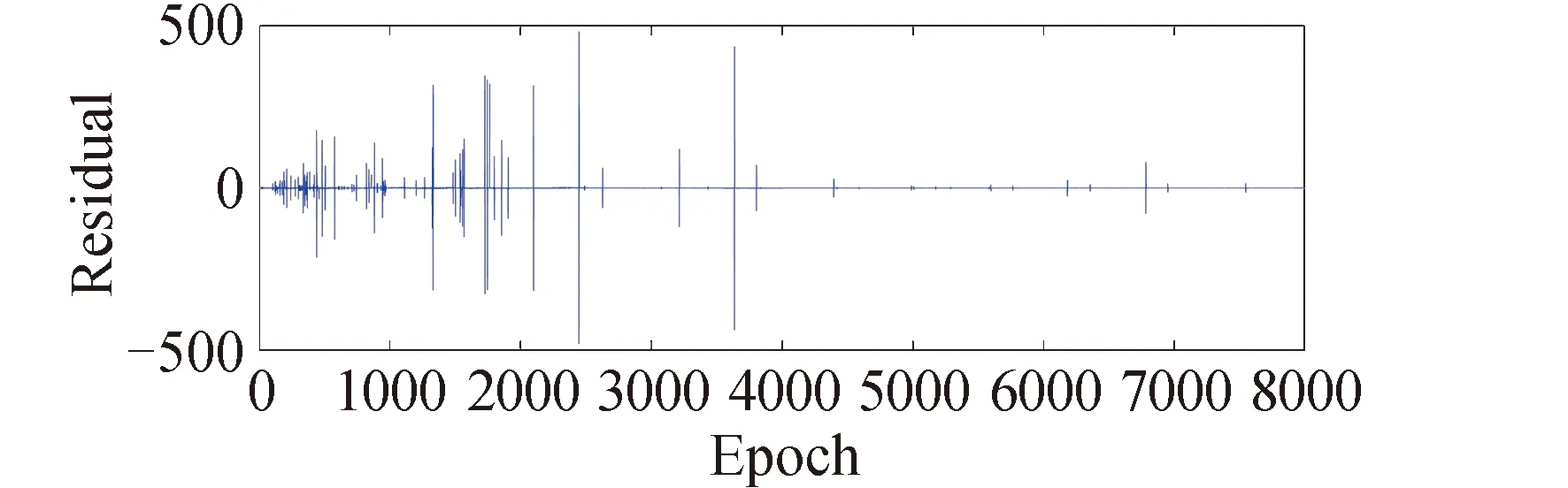
图4 实测数据的周跳探测结果

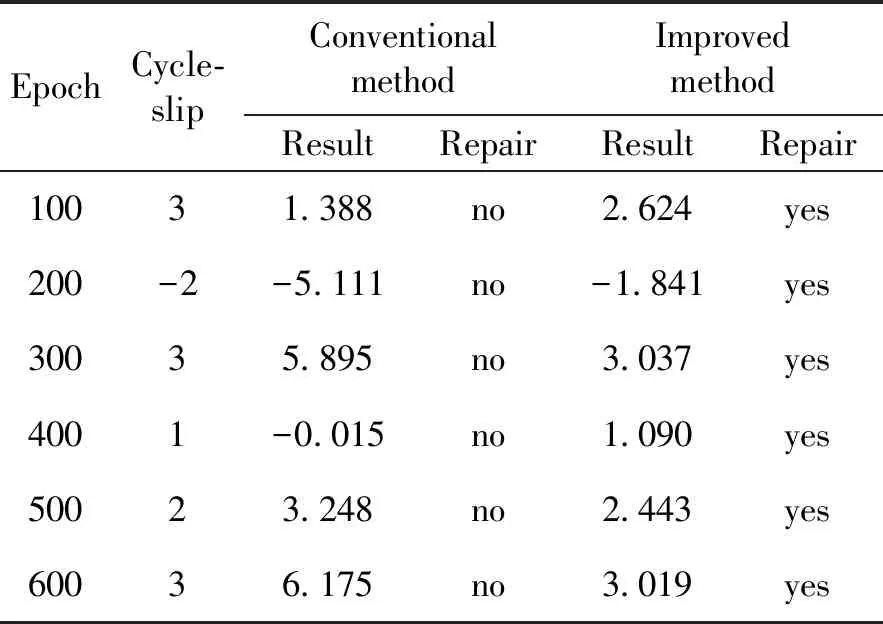
表2 两种方法周跳探测结果对比

分别使用传统的多普勒周跳探测法和基于卡尔曼滤波平滑多普勒值的周跳探测方法探测周跳,残差序列如图5和图6所示,探测结果如表2所示。因为当q(i)=10-8时周跳探测量的标准差约为0.3,本文取固定阈值δ=1以检验新算法对于小周跳的探测能力。可以看出由于多普勒观测值精度较低,传统多普勒周跳探测法难以准确检测出周跳,还会因观测值噪声较大导致大量未发生周跳的时刻被误判为存在周跳。但使用卡尔曼滤波平滑多普勒观测值之后可探测出一周以上的周跳的大小和位置,极大提升了探测成功概率。由表2可以进一步看出本文计算出的周跳探测量经过取整后得到的周跳结果与仿真周跳一致,因此本文的周跳探测量方法可以修复周跳。

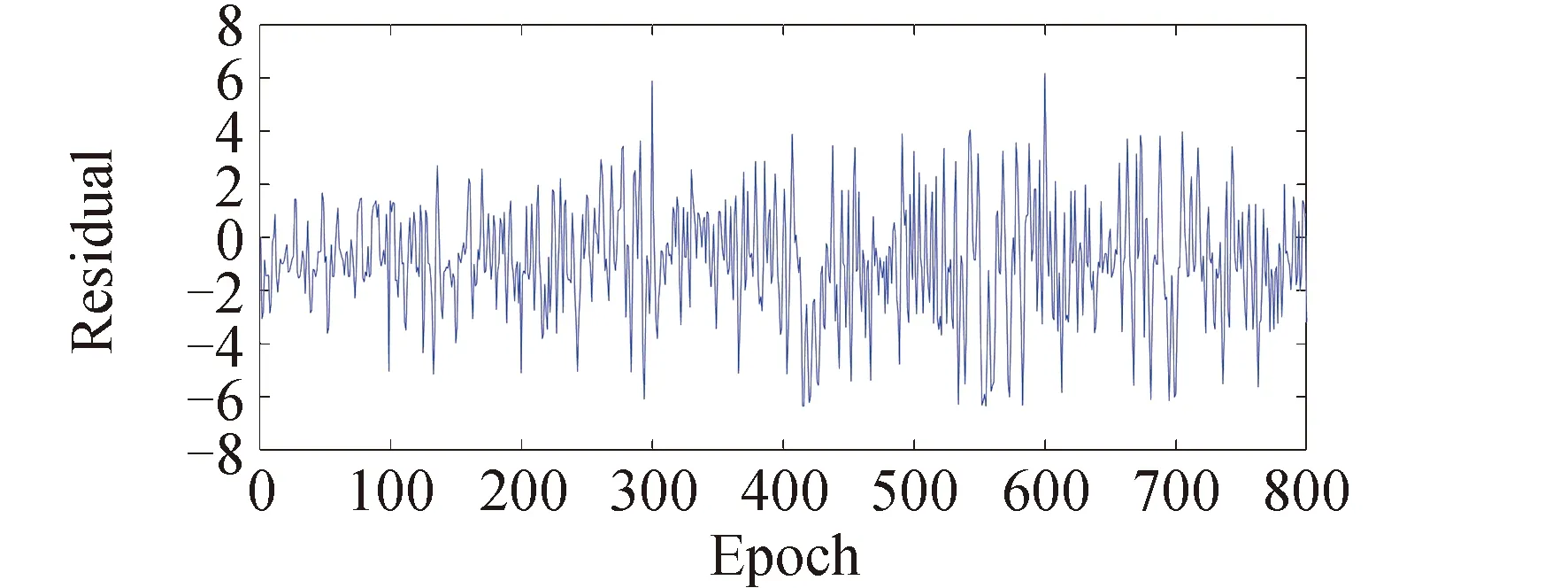
图5 模拟周跳情况传统的周跳探测法探测结果

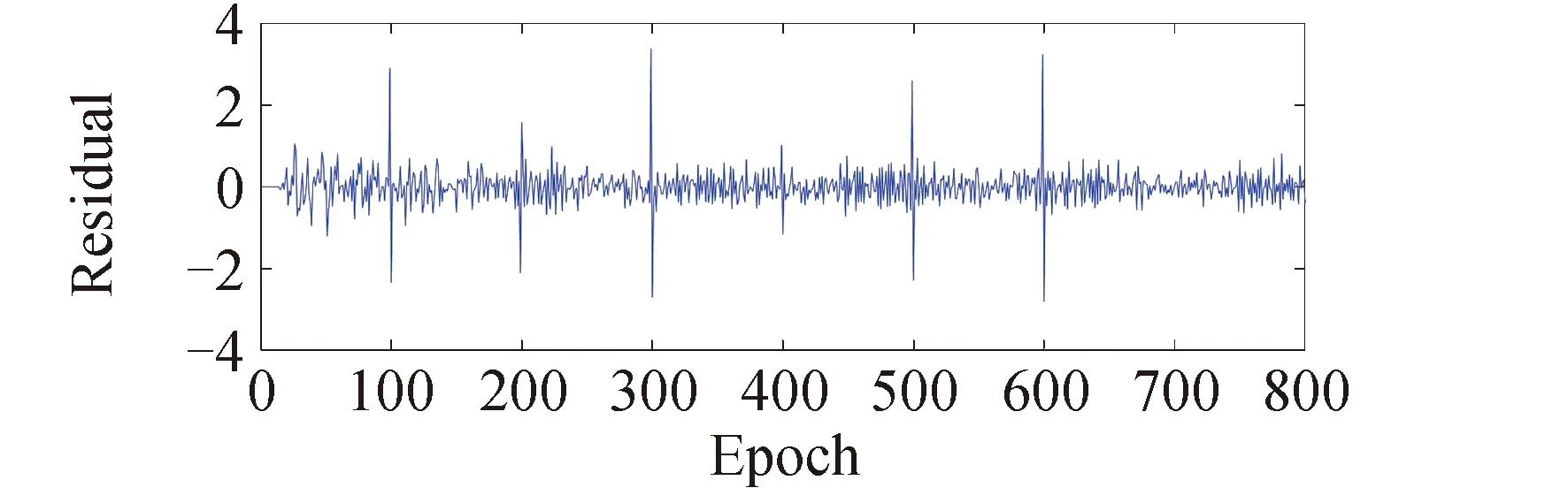
图6 模拟周跳情况改善的周跳探测法探测结果

4 结论

本文针对高轨卫星GNSS接收机接收到的多普勒观测值精度不高所导致的多普勒法难以探测周跳的问题,提出了基于卡尔曼滤波平滑多普勒观测值的周跳探测方法,并验证了本文提出的方法相对于传统多普勒法的优越性:

1)分别使用本文提出的方法和传统的多普勒法对实验数据的噪声水平进行检验,传统多普勒周跳探测法最大值到了6.3周,标准差为2.209,本文提出的方法周跳探测量最大值为1.2周,标准差为0.3047。因此,本文提出的方法比传统的多普勒法在低信噪比条件具有更好的检测能力。

2)分别使用本文提出的方法和传统的多普勒法进行周跳探测,传统多普勒法很难准确检测出周跳,还会因为噪声较大导致大量未发生周跳的时刻被误判为存在周跳;本文提出的方法可以准确地探测出高轨卫星载波相位观测数据中单个周跳的位置和大小,并能够对周跳进行修复。