改进的VMD-ITD 岩石声发射信号联合降噪方法

蔡改贫，李洋波，杨丽荣，黄祥海

（1.江西理工大学 机电工程学院，江西赣州 341000；2.江西省矿冶机电工程技术研究中心，江西赣州 341000）

声发射特征参数蕴含着丰富的岩石损伤渐进破坏的前兆信息，通过研究声发射特征，对于理解岩石破裂机理、预防因岩石破裂失稳而造成的事故具有十分重要的意义[1]。声发射技术可以提供岩体失稳所释放的大量信号源信息，因此可进一步判断岩体内部结构的动态变化、细观损伤的出现以及宏观裂纹的发展，因此国内外普遍运用声发射技术对岩体失稳现象进行识别与预测[2]。

VMD 是一种可变尺度的非平稳信号处理方法[3]，而ITD 对于大数据信号的实时处理有突出表现[4]，两种算法因其特点受到众多学者研究。Abdoos 等[5]将S 变换、VMD 与SVM 相结合，用于提取电能质量信号特征及模式识别，结果表明该方法识别分类效果良好；An 等[6]利用VMD 算法对轴系振动信号降噪处理，验证该算法对其降噪的有效性；张雪英等[7]通过VMD 与PNN 相结合，有效的提取特征信息，将齿轮故障诊断准确率提高至96.875%；Frei 等[8]提出ITD 算法，该方法在计算效率、分析精度、自适应划分等方面有突出表现，更适合对非平稳信号的分析。此外，郭力和邓喻[9]应用美国声学物理公司PAC 的PCI-2声发射实验仪器测量磨削声发射信号，并采用遗传算法优化BP 神经网络，使相对误差可控制在6.22%以下。李启月等[10]通过EEMD 与小波阈值的方法有效的消除噪声、趋势项的干扰，保留波形的真实信息，提高频谱的分析精度。

从之前学者的降噪算法研究中可以发现，不论是小波变换与EMD/EEMD，还是VMD 和ITD，虽然都能够实现对噪声的抑制，但在对某些特殊信号时其缺陷就会展现出来，如VMD 算法的模态数确定问题、ITD 算法的端点效应等。由于岩石声发射信号具有非平稳、大样本等特点，单一的降噪算法难以较好地抑制其噪声，因此利用多种算法进行联合降噪是值得考虑与有效的方法。

1 VMD、ITD 基本原理及改进VMD-ITD联合降噪算法

1.1 VMD 基本原理

VMD 分解算法通过对变分问题的构造及求解，在频域内实现信号的自适应分离，能够对信号的局部特征进行细致地刻画。VMD 算法将原始信号X分解为K个本征模态函数（Instrinsic mode function，IMF）uk(t)，假设每个uk(t)具有中心频率为 ωk的有限带宽，则可将其引入到变分问题中并对其进行求解，求解过程如下：

1）通过Hilbert 变换得到uk(t)的解析信号Xk(t)，并利用预估中心频率对Xk(t)进行调制得到信号Xωk(t)，即

式中Xk(t)为解析信号。

式中 δ(t)为单位脉冲函数。

2）通过解调信号的高斯平滑度，即梯度的L2范数的平方对带宽进行估计，其约束变分模型为：

式中：{uk}={u1,u2,···,uk}为IMF分量的集合；{ωk}={ω1,ω2,···,ωk}为分量对应的中心频率，Hz；u(t) 为输入信号；∂t为对t的偏导。

3）通过引入二次惩罚项 α在复杂噪声环境下提高信号的重构精度，并引入lagrange 算子 λ(t)保持约束条件严格性，进而将变分问题转化为非约束问题，得到的增广拉格朗日表达式为

式中：F(∗)为傅里叶变换；n为迭代次数。

综上所述，VMD 算法具体步骤如下：

1）将、、λ1以及n初始化；

2）根据式（5）、式（6）更新uk、ωk；

3）对λ 进行更新，更新式为

4）不断迭代，直到满足

式中 σ为判别精度。

当 σ满足设定的终止条件时，迭代不再继续，得到K个窄带模态分量；否则返回继续更新uk、ωk，直至满足式（8）。

1.2 ITD 基本原理

固有时间尺度分解（ITD）是一种适宜于大数据的实时处理以及非平稳信号分析的方法，它能够精确地提取信号的瞬时特征[11-12]。它通过构建基线信号将含噪声信号分解为多个固有旋转分量（PRC）以及一个残差分量，每个PRC 分量都包含信号的时频信息。ITD 分解原理如下：

1）定义Λ 为基线提取算子，则对于含噪待分解信号Xt的表达式为

式中：Lt=ΛXt为基线信号；Ht=(1-Λ)Xt，Ht为PRC分量。

2）求取信号Ht的所有局部极值点并将其所对应的时刻记为 τk,k=1,2,···N（N为极值点个数），且令τ0=0。为便于观察，分别用Xk和Lk表示X(τk)和L(τk)。若在 [0,τk]上Lt、Ht有定义，则信号Xt在时间[0,τk+2]范围内有意义，在连续极值点的区间(τk,τk+1]上定义分段线性提取算子 Λ，基线信号表达式为：

式中：α为线性缩放因子，用于控制PRC 分量的幅值，α ∈(0,1)，在工业应用中，α的大小与噪声水平有关，通常α 取0.5[13]。

ITD 分解全过程表达式为

式中：p为分解层数；为残余分量。

1.3 互信息的加权分量信号重构方法

互信息法（MI）能够反映某个分量包含原始信号的信息量，不同于相关系数，它不限于实值变量即具备一般性，且能较好的衡量非线性关系[14-15]。因此，本文采用互信息法进行信号重构，将各IMF 分量与原信号的互信息作为加权系数进行IMF 分量重构以达到降噪的目的。互信息的基本原理如下：

1）对于两个随机变量X、Y，它们的互信息I(X,Y)利用概率与熵的概念进行定义，定义式的表达式为

式中：P(x,y)为X、Y的联合概率分布函数；P(x)和P(y)分别为X、Y的边缘概率分布函数。

2）由于P(x,y)在一般情况下难以得到，通常采用核密度估计进行替代，本文中采用正态多元核密度估计，因此式（13）变换为

式中：n为样本数；h为核函数宽度；d为变量X的维数；T与d有关，当d=1时是方差，当d>1时是协方差矩阵，|T|为矩阵行列式。

互信息能够描述两个变量之间相关性，将其作为加权系数进行信号重构不会因舍弃某些分量造成信息丢失，并且能够抑制相关性小的含噪声分量，重构后的信号Xt表示为

式中：K为模态数；uk(t)为第K个分量；Ik(X、Y)为uk(t)与原信号的互信息。

1.4 改进VMD-ITD 的声发射信号联合降噪方法

VMD 分解过程中常用中心频率法[16-17]来确定模态数K的值，但这一方法容易受到人为主观因素的影响。针对上述问题，改进模态数K确定过程，并将其应用到改进VMD-ITD 的声发射信号联合降噪主要过程中，过程如下：

1）对原始信号X(t)进行VMD 分解，且将模态数K初始化为1，则得到一个IMF 分量u1(t)，计算u1(t)的能量E1的表达式为

其余参数都设为默认值。

2）将得到的前K个IMF 分量逐次累加，利用2-范数计算信号X(t)的能量E0，即

式中||X(t)为信号X(t)的2-范数。

分量能量比η 的计算式为

3）判断 η的值，由于所设定的能量阈值 θ=0.95。因此，若η<95%，则更新模态数即K=K+1并重复上述步骤直至达到终止条件；若 η ≥95%，则停止VMD 分解并输出K，得到K个分量uk(t)；

4）计算各分量与原信号的互信息Ik(X、Y)，并将其作为加权系数对各分量进行加权重构得到信号；

综上所述，改进VMD-ITD 联合降噪算法流程如图1所示。

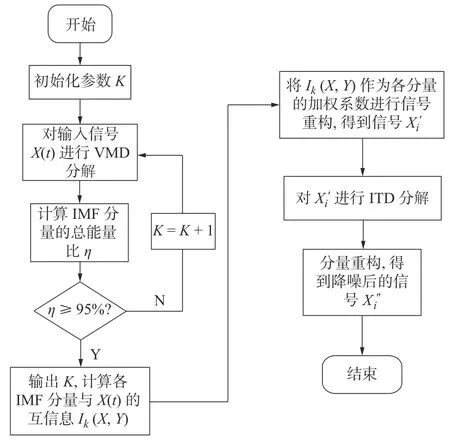
图1 联合降噪算法流程Fig.1 Joint denoising algorithm flowchart

2 仿真信号分析

2.1 仿真信号的构建

改进VMD-ITD 联合降噪算法从能量角度确定其模态数，并根据各分量与原始信号的互信息量进行加权重构，最后对重构信号进行ITD 二次降噪。为说明该方法对非平稳信号降噪的可行性与有效性，通过构造仿真信号进行降噪分析评价。实测信号中往往是多种类型信号进行叠加，因此本文结合Mitrakovic 等[18]与白瑞[19]的声发射信号数学模型，构建的仿真信号y(t)由3个分信号及一个强度为0.1的随机噪声 ζ(t)构成，其表达式为

式中：Ai为第i个信号的幅值，V；αi为第i个信号的衰减系数；fi为第i个信号的频率，Hz。

根据构造的声发射数学模型，可以得到其加噪仿真的信号，并计算其频谱，加噪仿真信号及其频谱如图2所示。

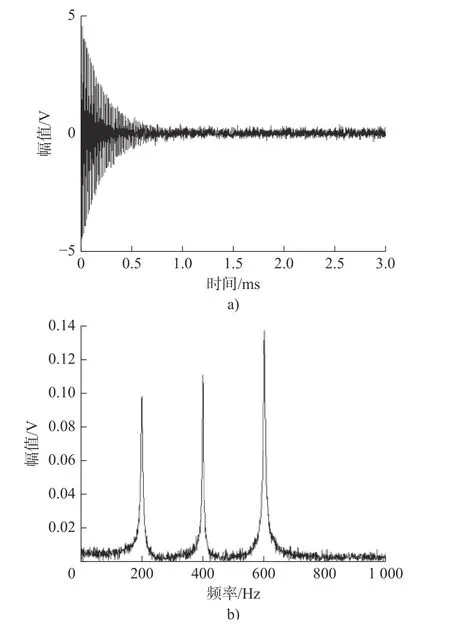
图2 加噪仿真信号及其频谱Fig.2 A simulated noisy signal and its spectrum

2.2 仿真信号的降噪结果分析

首先利用本文提出的基于分量能量比的改进VMD 对仿真信号进行分解，当达到终止条件（η ≥95%）时，得到一系列的IMF 分量如图3所示。

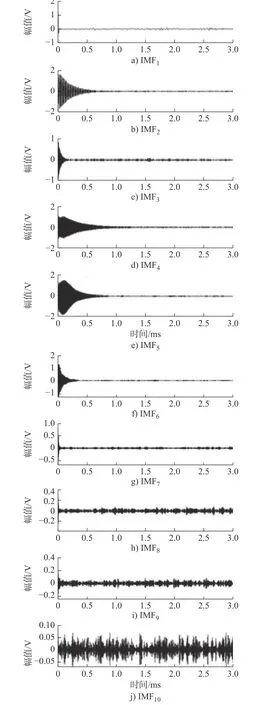
图3 仿真信号的IMFFig.3 IMF of the simulated signal

由图3可知，通过分量能量比来确定模态数k=10，分解结果表明该方法能够有效将各分信号分离；并且部分分量信号与原信号差异较大，如IMF1、IMF7、IMF8、IMF9和IMF10，这表明这些分量信号是与原信号相关性较低的噪声分量。计算各分量的频谱，结果如图4所示。

图4 各IMF 的频谱Fig.4 Spectrum of each IMF

由图4可知，分量IMF2～IMF7基本都在仿真信号的频率上（200、400、600 Hz），其余分量频率分布在更低的100 Hz 附近或更高的900 Hz 以上频段内，说明IMF2～IMF7含有原始仿真信号的最主要信息，而其余分量包含的大多是噪声信息。为抑制这些噪声且尽可能保留完整信息，将所有分量与原信号的互信息量作为加权系数来重构信号，得到的各IMF 与加噪仿真信号的互信息如表1所示。

表1 各IMF 与加噪仿真信号的互信息量Tab.1 Mutual Information between each IMF and the simulated noisy signal

由表1可知，IMF1、IMF7、IMF8、IMF9和IMF10的互信息量明显小于其他分量，说明这些分量包含原信号有效信息更少，这与实际波形也相符；在10个IMF 中互信息量最大的IMF5其值为0.591，说明IMF5包含较多的有效信息。根据式（17）对各分量进行加权得到重构信号，再通过ITD 分解并二次重构以达到进一步降噪的目的，得到的二次降噪信号及其频谱如图5所示。

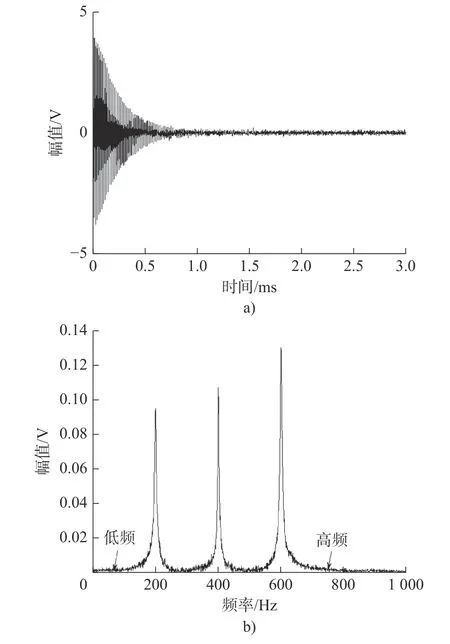
图5 二次降噪信号及其频谱Fig.5 The second-order denoised signal and its spectrum

对比图2和图5可知，经过ITD 二次降噪的信号其频谱在高频和低频部分更加光滑，毛刺明显减少，说明在改进VMD-ITD 能够将信号的高频和低频噪声滤除。为评价改进VMD-ITD 降噪性能，通过计算其降噪后的信噪比和均方根误差并与VMD、ITD 算法进行对比，得到3种算法对同一信号降噪后的信噪比与均方根误差对比结果如表2所示。

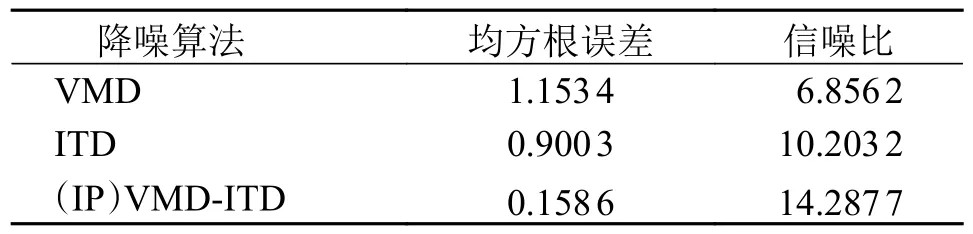
表2 3种算法降噪后信号的信噪比与均方根误差Tab.2 Signal-to-noise ratio (SNR) and root mean square error (RMSE) of the denoised signals using three algorithms

由表2可知，改进VMD-ITD（（IP）VMD-ITD）算法的均方根误差为0.158 6，在3种方法中最小，且其信噪比为14.287 7，明显高于另外两种方法，说明相比于单一的VMD、ITD 降噪方法本文提出的方法降噪性能更好，能够在保留更多有效信息的前提下提高信噪比。

3 改进VMD-ITD 降噪算法在岩石声发射信号处理中的应用

本次试验由单轴压缩试验平台和声发射信号采集平台两部分组成，其中单轴压缩试验平台采用无锡欧凯电子的万能材料试验机搭建的，该试验机由控制台和压力机两部分组成，控制系统由液压动力源提供稳定输出，控制系统通过液压源控制压力机的压头进行试验。单轴试验平台如图6所示。

图6 万能材料试验系统Fig.6 Universal material testing system

声发射信号采集平台由声华科技的双通道声发射仪搭建而成，主要有声发射传感器、前置放大器、信号采集卡以及采集系统等几个部分。其中声发射传感器是感知声发射现象的必备器件，它的性能参数影响着信号的采集，本次试验选用的传感器参数如表3所示。

表3 传感器SR150M 的基本参数Tab.3 Basic parameters of the sensors

声发射传感器安装在试件中部轴线位置，为保证传感器与试件紧密贴合，两者的接触面采用真空脂作为耦合剂并用透明胶布进行固定，传感器布局如图7所示。所准备的岩样为钨岩，如图8所示。

图7 传感器布局Fig.7 Sensor layout

图8 钨岩岩样Fig.8 Tungsten rock sample

为验证本文提出方法在岩样破裂声发射信号噪声抑制的有效性，从钨岩破裂试验中随机选取一组声发射信号进行降噪分析，选取的声发射信号波形及其频谱如图9所示。

图9 含噪原始信号及其频谱Fig.9 Noise-containing original signal and its spectrum

运用改进VMD 对原始信号进行分解，根据分量能量比得到各IMF 分量如图10所示。

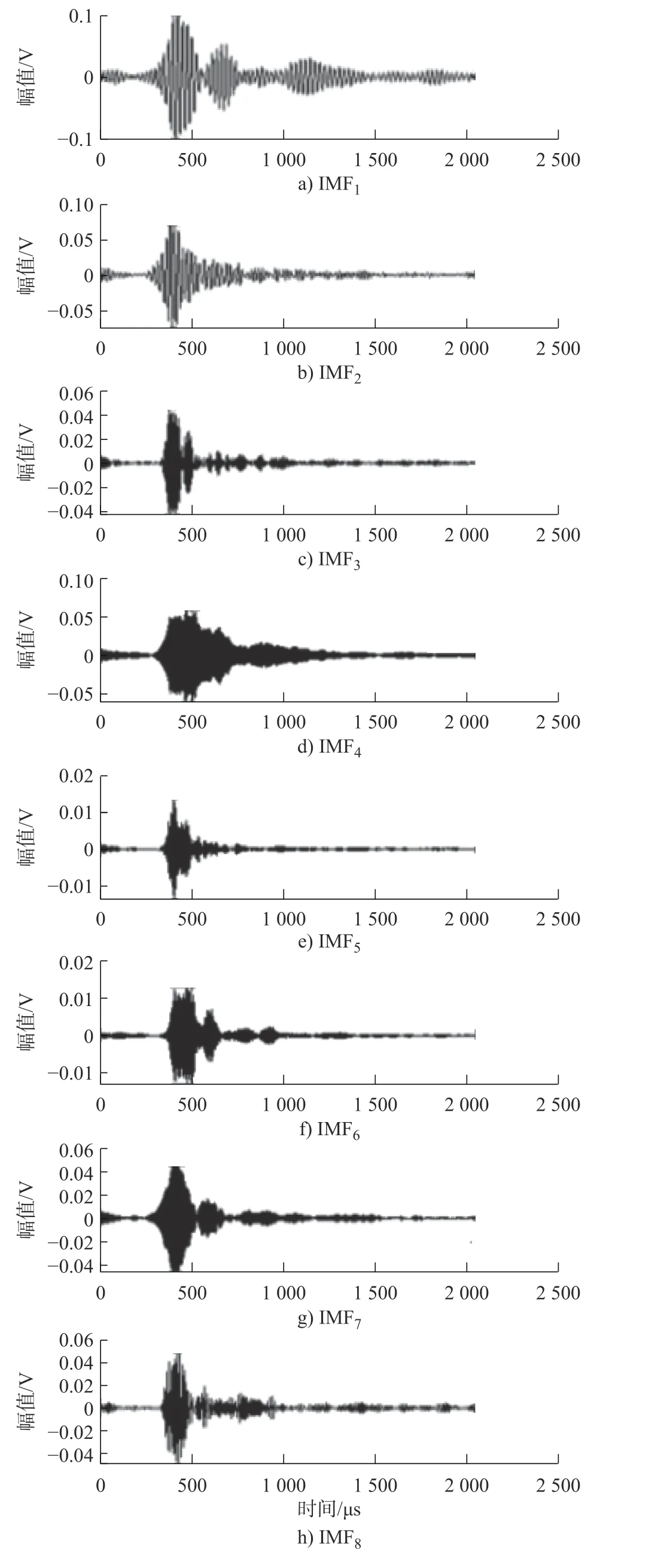
图10 含噪原始信号的IMFFig.10 IMFs of the noise-containing original signal

由图10可知，分量能量比大于95%时原信号分解为8个IMF 分量，即分解模态数k=8；在所有分量中，IMF1与IMF2能较好地反映原信号波形，其余分量存在部分重叠。计算所有分量与原信号的对应互信息，结果如表4所示。

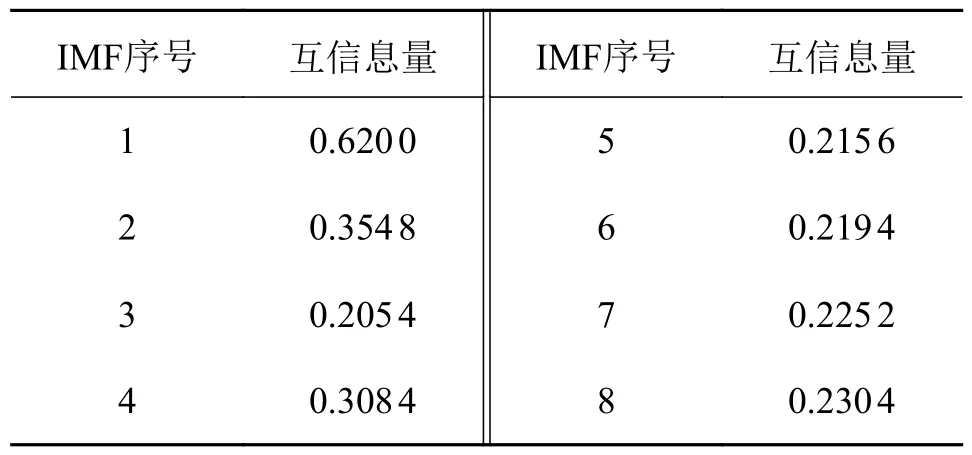
表4 各IMF 与含噪原始信号的互信息量Tab.4 Mutual information between each IMF and the noise-containing original signal

由表4可知，IMF1的互信息量为0.620 0，在所有分量中最大，说明IMF 包含原信号有效信息最多，这与实际波形也相符，而其他分量的互信息量相差不大，说明包含的原始信号有效信息较少。将各分量进行加权得到重构信号，再对重构信号进行ITD 分解并重构得到二次降噪信号，两次重构信号的波形及频谱如图11和图12所示。

图11 基于加权分量一次重构信号及其频谱Fig.11 First-reconstructed signal using weighted components and the signal’s spectrum

图12 二次降噪重构信号及其频谱Fig.12 Second denoised reconstructed signal and its spectrum

对比图9、图11及图12可知，经过ITD 二次降噪的信号其频谱在高频部分更加光滑，毛刺明显减少，说明在改进VMD-ITD 能够将信号的高频噪声滤除。为评价改进VMD-ITD 的降噪性能，通过计算其降噪后的信噪比和均方根误差并与VMD、ITD 算法进行对比，得到3种算法对同一实测含噪信号降噪后的信噪比与均方根误差结果对比如表5所示。

表5 3种算法降噪后信号的信噪比与均方根误差Tab.5 Signal-to-noise ratio (SNR) and root mean square Error (RMSE) of the denoised signals using three algorithms

由表5可知，改进VMD-ITD（（IP）VMD-ITD）算法的均方根误差为4.552 1，在3种方法中最小，且其信噪比为10.012 8，高于另外两种方法，说明本文提出的改进VMD-ITD 方法在岩样破裂声发射信号降噪中的可行性与有效性，且相比于VMD、ITD 算法对噪声抑制的能力更强。

4 结论

1）采用分量能量比从能量角度来确定VMD 的分解模态数k，并利用互信息法对分量进行加权重构，相比中心频率法与相关系数法能更好地突出有效分量同时抑制噪声分量，减少因剔除某些分量而造成的误差。

2）运用改进VMD-ITD 联合降噪算法抑制非平稳信号中的噪声相比单一的VMD、ITD 算法，其均方根误差更小且信噪比更大，说明利用改进VMD-ITD对信号进行降噪能够有效抑制噪声，进一步提高信号的可靠性。

3）改进VMD-ITD 算法对岩样声发射破裂信号降噪处理能够有效地抑制岩样在破裂过程中的噪声信号，提取出原始声发射信号中的大部分有效信息，提高后续信号分析的有效性。